六面体单元在压印成形模拟中的应用

易国锋 李巧敏 钟 文 柳玉起

1.湖北工业大学机械工程学院，武汉， 4300742.华中科技大学材料成形与模具技术国家重点实验室，武汉, 430074

六面体单元在压印成形模拟中的应用

易国锋1李巧敏2钟 文2柳玉起2

1.湖北工业大学机械工程学院，武汉， 4300742.华中科技大学材料成形与模具技术国家重点实验室，武汉, 430074

针对动力显式压印成形模拟系统COINFORM中单点积分单元的沙漏问题，建立了一种采用多点积分方案的八节点六面体单元。推导了体积闭锁和剪切闭锁的产生机理，采用假设应变法，成功消除了单元在近似不可压缩变形中的体积闭锁和弯曲变形中的剪切闭锁。将建立的六面体单元与COINFORM相结合，对银999纪念币压印成形模拟算例进行了分析。研究结果表明，提出的多点积分六面体单元在压印模拟中不存在闭锁现象，且比COINFORM原有单元具有更高的计算精度。

多点积分；闭锁现象；纪念币；压印成形

0 引言

压印成形是纪念币[1]的主要制造工艺。虽然压印工艺拥有悠久的历史，但是由于纪念币材料和行业的特殊性，其制造技术和工艺规程均需严格保密。这导致目前已公开文献中，与纪念币压印技术相关的资料比较少，国内外纪念币的设计与制造主要依赖各造币企业长期积累的经验。由于工程经验难以有效地预测压印成形工艺中的材料流动和成形缺陷，故目前纪念币行业中仍然存在制造周期长、废品率高的问题[2]。据统计，目前国内造币行业纪念币压印的废品率在10%以上，大直径、精细花纹和大镜面纪念币的废品率甚至达到50%。

为了有效弥补传统压印工艺存在的不足，BREKELMANS等[3]、BUFFA等[4]、GUO等[5-6]采用DEFORM-3D、ABAQUS和MARC等通用软件，对压印成形的有限元数值模拟展开了研究。但是，由于上述软件采用的是隐式算法，故不仅对计算规模有限制，而且难以保证收敛性。为了突破计算规模的限制，XU等[7]对压印成形工艺及其数值模拟技术进行了深入研究，建立了纪念币压印成形模拟系统COINFORM，实现了可达1000万个单元的大规模压印成形模拟。但是，在单元选择方面，COINFORM采用的是单点积分的八节点六面体单元，在压印成形过程中可能产生非物理变形模式。为了改善COINFORM的仿真性能，有必要在COINFORM中嵌入一种精度更高、稳定性更好的实体单元。一般认为，八节点六面体单元比四节点四面体单元具有更高的稳定性[8]。在六面体单元的早期研究中，FLANAGAN等[9]针对单点积分单元的沙漏模式，提出了一种根据经验设置沙漏系数的扰动沙漏控制方法。HALLQUIST[10]在DYNA3D中给出了另一种用于单点积分的沙漏控制算法，尽管该方法拥有较高的计算效率，但由于沙漏力与刚体转动不正交，故并不适用于刚体转动较大的变形分析。此后，BELYTSCHKO等[11]基于假设应变法建立了一个消除了闭锁问题的减缩积分八节点六面体单元，根据单元几何形状和材料属性自动计算沙漏力，避免了人工参数的输入。ZHU等[12]开发了一系列假设应变混合单元，并对单元的闭锁问题和沙漏现象展开了研究。LIU等[13]开发了多点积分单元HEXDS，并将其应用于大变形弹塑性分析。WANG等[14]开发了一个全积分单元，忽略诱发闭锁的应变项以消除闭锁问题，并将其应用于板料成形分析。OOI等[15]采用组合的形函数开发了一个八节点六面体单元，该单元通过了分片测试，能够适应扭曲的单元形状。FREDRIKSSON等[16]通过对高阶应变场的适当选取，消除了剪切闭锁和沙漏模式，开发了一种高精度的实体单元。从单元的研究历程可以看出，沙漏模式、体积闭锁和剪切闭锁是六面体单元的主要缺陷。若要建立一种精确稳定的六面体单元，首先需要避免以上几种缺陷。

本文针对COINFORM中已有单元的沙漏问题，提出了一种多点积分的八节点六面体单元。为了消除多点积分方案导致的闭锁现象，通过假设应变法对体积闭锁和剪切闭锁进行了处理。将提出的六面体单元与COINFORM相结合，对纪念币压印算例进行了分析。

1 单元几何

本文开发的八节点六面体单元如图1所示。每个节点有3个平移自由度，无转动自由度。建立图1所示的自然坐标系，ξ、η、ζ为自然坐标系的三个坐标轴。自然坐标系(x,y,z)和笛卡儿坐标系通过Jacobian矩阵J关联：

(1)

图1 四点积分的八节点六面体单元Fig.1 8-node hexahedral element with four integration points

单元采用多点积分方案，4个高斯积分点在自然坐标系下的坐标分别为

(2)

2 单元形函数

任意积分点在共旋坐标系下的坐标(x,y,z)T和位移(u,v,w)T可以插值表示为

(Nx,Ny,Nz)T

(3)

(Nu,Nv,Nw)T

(4)

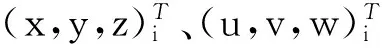
Ni=(1+ξiξ+ηiη+ζiζ+ξiηiξη+ηiζiηζ+

ξiζiξζ+ξiηiζiξηζ)/8

(5)

构成形函数向量

N=(s+ξξ+ηη+ζζ+h1ξη+h2ηζ+h3ξζ+

h4ξηζ)/8

(6)

由式(3)和式(6)可以得到笛卡儿坐标(x,y,z)T与自然坐标(ξ,η,ζ)T的转换关系式：

[ξηζ]T=C[x-txy-tyz-tz]T

(7)

(8)

(9)

将式(7)代入式(6)可得

N=Δ+bxx+byy+bzz+γ1ξη+γ2ηζ+

γ3ξζ+γ4ξηζ

(10)

上式包含8个行向量：

(11)

α=1,2,3,4

从式(10)可以看出，单元发生沙漏模式变形时，单元中心点(ξ=0,η=0,ζ=0)处的应变能为零，因此，COINFORM中原有的单点积分单元容易在压印成形模拟中诱发沙漏模式。对于多点积分单元，式(10)中的γα能保证单元刚度矩阵满秩[12]，提高单元的稳定性。

3 非线性闭锁控制

3.1 标准B矩阵

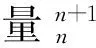
(12)

标准应变-位移矩阵B与形函数向量N相关[17]，其多项式展开形式为

B(ξ,η,ζ)=B0+ξBξ+ηBη+ζBζ+ξηBξη+

ηζBηζ+ξζBξζ

(13)

其中，B0用bx、by和bz表示，Bλ(λ=ξ,η,ζ,ξη,ηζ,ξζ)用下式中相应的bxλ、byλ和bzλ表示：

(14)

3.2 闭锁现象

3.2.1 体积闭锁

(15)

结合式(12)和式(15)，有

(16)

3.2.2 剪切闭锁

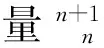
(17)

3.3 假设应变法

(18)

(19)

(20)

为了使剪切闭锁的处理更加简洁，在单元内建立共旋坐标系(r1,r2,r3)，满足

(21)

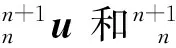
(22)

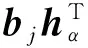
4 数值算例

图2所示为某银999纪念币，纪念币的正反面图案相同，镜面区域的厚度为2.0 mm。采用图3所示1盎司(28.3495 g)标准坯饼成形该纪念币，由于保密原因，具体尺寸未在图中标注。压印实验采用造币专用设备，压印机为3500 kN压印机。实验过程中,压机运动速度为100 mm/s，模具的有效行程为0.43 mm。随着上模向下运动，压印力不断增大，最终达到最大值1600 kN，获得填充比较饱满的纪念币，如图4所示。

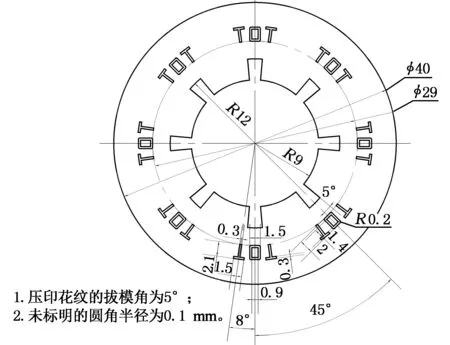
图2 纪念币几何尺寸Fig.2 Geometry of the commemorative coin

图3 带有边形的1盎司(28.3495 g)银999坯饼Fig.3 The 1-ounce (28.3495 g)Ag999 workpiece with flange

图4 压印实验获得的纪念币Fig.4 A commemorative coin obtained by the experiment

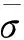
(a)坯饼 (b)印模

(c)中圈 (d)装配模型图5 压印成形有限元模型Fig.5 Finite element model of the coining

采用本文提出的多点积分六面体单元模拟纪念币的压印成形过程。成形结束后纪念币的应力和应变分布如图6所示。可以看出，由于纪念币图纹区域模具圆角较小，齿状图纹和字符“TOT”处出现了应力集中，且应力梯度和应变梯度较大。

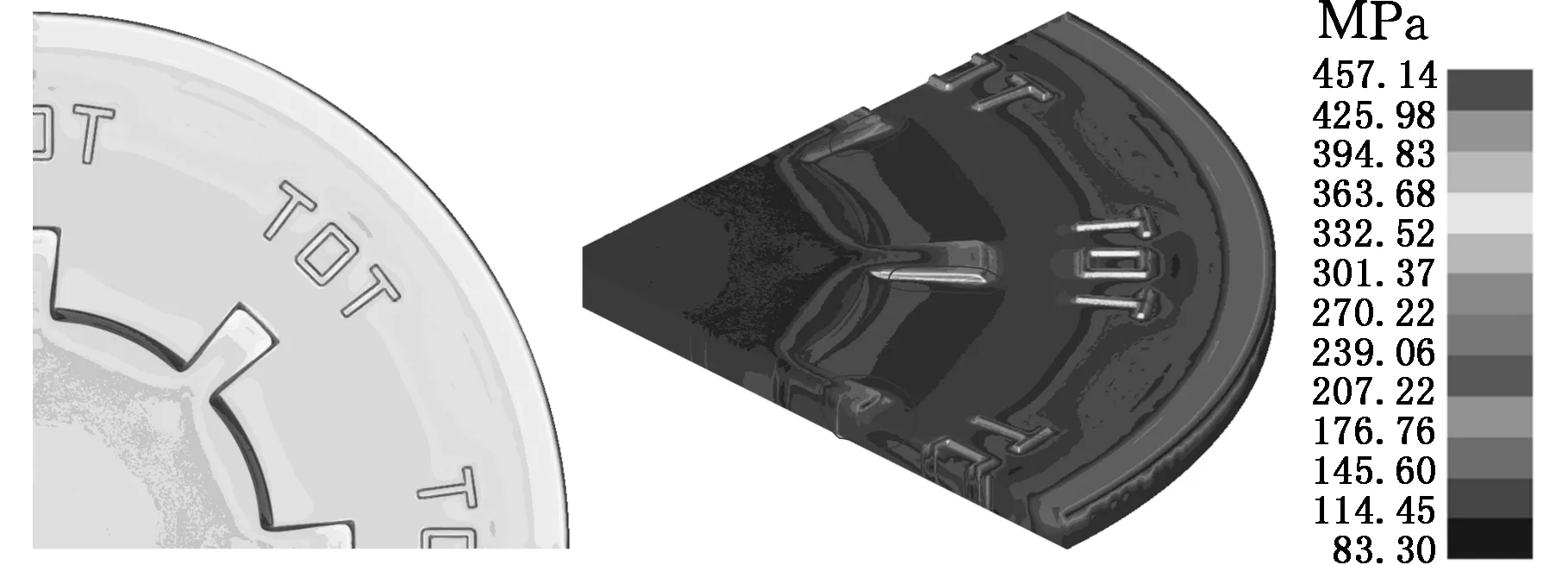
(a)等效应力

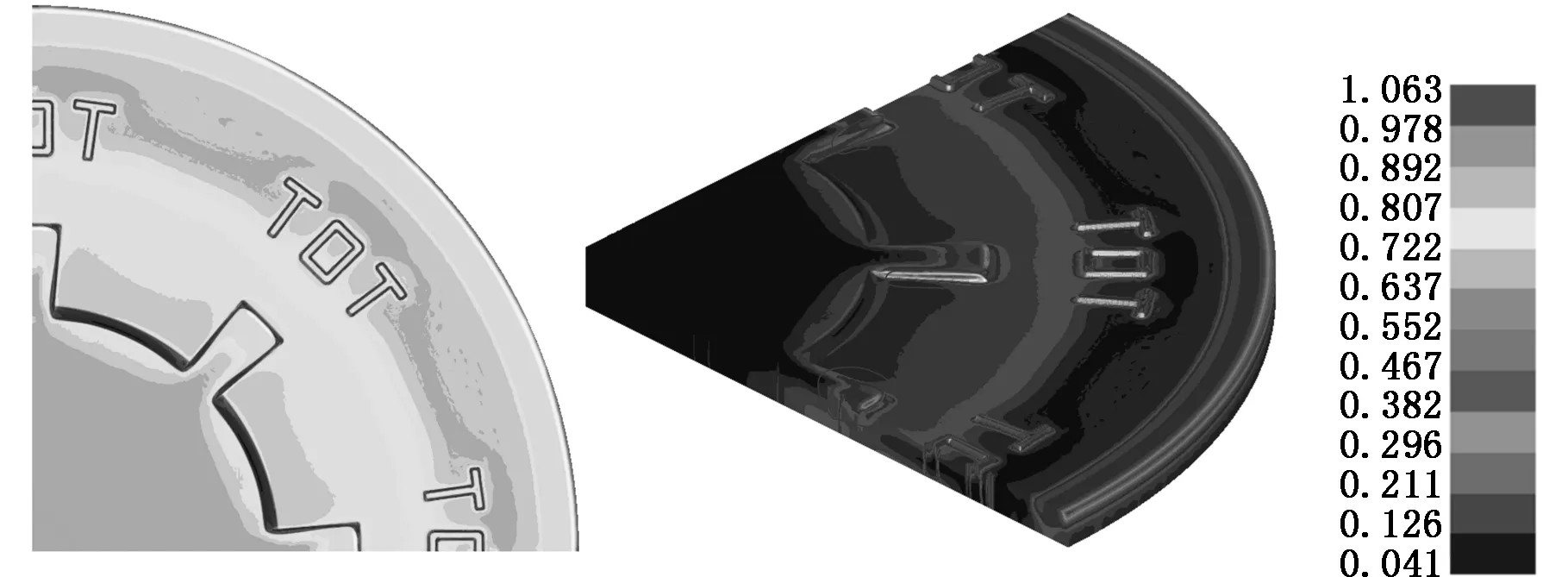
(b)等效应变图6 纪念币的应力和应变分布Fig.6 Stress and strain distributions of the commemorative coin

此外，由于边形区域的材料较早地流向中圈，产生的塑性变形较大，故压印结束后边形区域也出现了应力集中。

为了验证单元的稳定性，图7给出了成形过程中压印力随模具行程的变化曲线(数据已处理为对应整个模型)，并与COINFORM原有单点积分单元[7]的计算结果进行对比。其中，单点积分单元采用黏性沙漏控制，沙漏系数取0.1。从图7可以看出，印模与坯饼在O点接触，最先发生接触处位于坯饼的边形表面。在OA阶段，坯饼边形在印模的作用下发生塑性流动，材料沿径向流向中圈。在A点处，边形区域基本被压平，整个坯饼表面与模具接触，因此，AB阶段压印力直线增大。在模具外力的作用下，金属从B点开始填充模具型腔，此时外力不断增大，但增速小于AB阶段。从C点开始，坯饼的外边缘与中圈完全接触，金属在外力作用下实现图纹的完全填充，这一过程需要较大的压印力才能实现。在CE阶段,多点积分单元模拟获得的压印力不断增大，与实验中压印力的变化趋势相同。模具在E点到达下死点，压印力达到最大值1495 kN，与实验结果接近。但是，随着塑性变形的增大，单点积分单元在D点处产生沙漏模式，压印力突然呈减小趋势，这与实验结果差别较大。单点积分单元的沙漏模式逐渐传播，最终导致计算失败。由此可见，OD阶段两种单元的计算结果非常接近，说明假设应变法成功消除了单元的体积闭锁和剪切闭锁；D点之后，多点积分单元相比黏性沙漏控制的单点积分单元体现出了更高的稳定性。

图7 压印力随行程变化的曲线Fig.7 Coining force varying with the stroke

5 结论

(1)相比单点积分六面体单元，本文提出的多点积分六面体单元具有更高的稳定性。

(2)通过假设应变法，有效消除了多点积分六面体单元的体积闭锁和剪切闭锁。

(3)本文提出的六面体单元用于COINFORM压印成形模拟能达到较高的精度。

[1] 俞晓萍. 北京奥运会纪念币—从中国走向世界[J].中国金币,2008(9):13-14. YU Xiaoping. Commemorative Coins for Beijing Olympic Games-from China to the world[J]. China Gold Coin,2008(9):13-14.

[2] 钟文，柳玉起，许江平，等. 金银纪念币压印成形中的缺陷预测[J]. 中国机械工程,2012,23(1):109-112. ZHONG Wen, LIU Yuqi, XU Jiangping, et al. Defect Prediction in Coining Process for Au-Ag Commemorative Coins[J]. China Mechanical Engineering,2012,23(1):109-112.

[3] BREKELMANS W A M, MULDERS L H G, RAMAEKERS J A H, et al. The Coining Process: analytical Simulations Evaluated[J]. CIRP Annals—Manufacturing Technology,1988,37(1):235-238.

[4] BUFFA G, FRATINI L, MICARI F. The Relevance of the Preform Design in Coining Processes of Cupronickel Alloy[C]//Proceedings of the 9th International Conference on Numerical Methods in Industrial Forming Processes. Oporto,2007:1005-1010.

[5] GUO K, WANG X, BELL R, et al. The Experimental Evaluation of Friction Conditions during a Silver Coining Process[J]. Steel Reesearch International,2008,79(2):80-87.

[6] GUO K. Development of Design Tools for Coining Process Using FEM[D]. Ottawa: Carleton University,2009.

[7] XU J P, LIU Y Q, LI S Q, et al. Fast Analysis System for Embossing Process Simulation of Commemorative Coin-COINFORM[J]. Comput. Model. Eng. Sci.,2008,38(3):201-216.

[8] BENZLEY S E, PERRY E, MERKLEY K, et al. A Comparison of All Hexagonal and All Tetrahedral Finite Element Meshes for Elastic and Elasto-plastic Analysis[C]//Proceedings, 4th International Meshing Roundtable. Albuquerque,1995:179-191.

[9] FLANAGAN D P, BELYTSCHKO T. A Uniform Strain Hexahedron and Quadrilateral with Orthogonal Hourglass Control[J]. International Journal for Numerical Methods in Engineering,1981,17(5): 679-706.

[10] HALLQUIST J O. LS-DYNA Theory Manual Theory Manual[M]. Livermore: Livermore Software Technology Corporation,2014.

[11] BELYTSCHKO T, BINDEMAN L P. Assumed Strain Stabilization of the Eight Node Hexahedral Element[J]. Computer Methods in Applied Mechanics and Engineering,1993,105(2):225-260.

[12] ZHU Y Y, CESCOTTO S. Unified and Mixed Formulation of the 8-node Hexahedral Elements by Assumed Strain Method[J]. Computer Methods in Applied Mechanics and Engineering,1996,129(1):177-209.

[13] LIU W K, GUO Y, TANG S, et al. A Multiple-quadrature Eight-node Hexahedral Finite Element for Large Deformation Elastoplastic Analysis[J]. Computer Methods in Applied Mechanics and Engineering,1998,154(1):69-132.

[14] WANG J, WAGONER R H. A Practical Large-strain Solid Finite Element for Sheet Forming[J]. International Journal for Numerical Methods in Engineering,2005,63(4):473-501.

[15] OOI E T, RAJENDRAN S, YEO J H, et al. A Mesh Distortion Tolerant 8-node Solid Element Based on the Partition of Unity Method with Inter-element Compatibility and Completeness Properties[J]. Finite Elements in Analysis and Design,2007,43(10):771-787.

[16] FREDRIKSSON M, OTTOSEN N S. Accurate Eight-node Hexahedral Element[J]. International Journal for Numerical Methods in Engineering,2007,72(6):631-657.

[17] ZIENKIEWICZ O C, TAYLOR R L, ZHU J Z. The Finite Element Method: Its Basis and Fundamentals[M]. Burlington: Elsevier Butterworth-Heinemann,2005:733-734.

(编辑 陈 勇)

A Hexahedral Element Applied to Coining Simulations

YI Guofeng1LI Qiaomin2ZHONG Wen2LIU Yuqi2

1.School of Mechanical Engineering, Hubei University of Technology, Wuhan, 430074 2.State Key Laboratory of Materials Processing and Die & Mould Technology,Huazhong University of Science and Technology, Wuhan, 430074

In order to overcome the hourglass problems of the one-point integrated element used in the dynamic explicit coining simulation system COINFORM, a new multi-point integrated 8-node hexahedral element was proposed herein. The generation mechanism of volume locking and shear locking was deduced. With the assumed strain method, the volumetric locking in near-incompressible deformations and the shear locking in bending situations were avoided. Combined with COINFORM, the proposed hexahedral element was applied to the coining simulation of a Ag999 commemorative coin. The results show that the locking phenomena of the multi-point integrated element are successfully avoided in the coining simulation, and the proposed element achieves higher computational accuracy than that of the existing element of COINFORM.

multi-point integration; locking phenomena; commemorative coin; coining

2016-10-08

国家自然科学基金资助项目(51275184)

O344.3；TP391.9

10.3969/j.issn.1004-132X.2017.15.017

易国锋，男，1976年生。湖北工业大学机械工程学院讲师。主要研究方向为金属塑性成形模拟及模具设计。E-mail：churchwell@163.com。李巧敏，女，1989年生。华中科技大学材料成形与模具技术国家重点实验室博士后研究人员。钟 文，男，1988年生。华中科技大学材料成形与模具技术国家重点实验室博士后研究人员。柳玉起(通信作者)，男，1966年生。华中科技大学材料成形与模具技术国家重点实验室教授、博士研究生导师。