装载机工作装置疲劳试验载荷谱编制方法

万一品 宋绪丁 员征文 郁录平

1.长安大学道路施工技术与装备教育部重点实验室，西安，7100642.徐工集团江苏徐州工程机械研究院，徐州，221004

装载机工作装置疲劳试验载荷谱编制方法

万一品1宋绪丁1员征文2郁录平1

1.长安大学道路施工技术与装备教育部重点实验室，西安，7100642.徐工集团江苏徐州工程机械研究院，徐州，221004

为研究装载机工作装置疲劳性能，提出了一种考虑分段载荷均值特性的工作装置疲劳试验程序载荷谱的编制方法，采集了4种典型物料铲装作业时工作装置的销轴载荷信号，并将销轴载荷转化为铲斗斗尖处的当量载荷。根据载荷特性,将每个作业周期分为空载行进、物料铲装、满载运输和物料卸载4段，完成了载荷的平稳性检验。采用雨流计数法分析各个作业段载荷的均幅值分布特性，结果表明：4个作业段的载荷均值服从正态分布，幅值服从三参数威布尔分布，且均值和幅值分布相互独立。对载荷进行频次外推和合成，并根据均幅值概率分布函数和波动中心法，编制了工作装置8级二维载荷谱和变均值疲劳试验程序加载谱。提出的载荷谱编制方法和结果可为装载机工作装置结构寿命预测及疲劳可靠性台架试验提供参考。

装载机；工作装置；斗尖当量载荷；载荷谱；疲劳试验

0 引言

在装载机作业过程中，工作装置会受到连续的随机载荷作用。工作装置在设计阶段通常需要基于寿命理论进行产品可靠性分析，在寿命预测及可靠性台架试验前，必须确定与工作装置实际作业工况相符的载荷谱[1]。利用实测载荷时间历程编制的载荷谱在室内台架试验中可以较好地再现工作装置所承受的随机载荷，且能提高试验效率，因此，在处理随机载荷时，常用程序载荷谱来表示结构所受载荷时间历程[2-3]。航空和汽车领域对载荷谱的研究已相对成熟，如闫楚良等[4]借助当量寿命概率分布，保持载荷时间历程与状态参数一致，编制了飞机结构的疲劳载荷谱；于佳伟等[5]在汽车室内模拟试验中，将汽车实测载荷时间历程编制成试验用载荷谱，并将其应用于整车耐久性试验中。对装载机载荷谱的研究多集中在传动系，张云龙等[6-7]参照飞机的“飞续飞”编谱策略，编制了装载机传动系“铲续铲”的分段载荷谱；文献[8]应用雨流计数法和数理统计法编制了汽车车身台架疲劳程序载荷谱，通过强度分析验证了程序谱的有效性。

对装载机工作装置载荷谱编制方法的相关研究较少，本文基于实测的铲斗销轴处载荷时间历程，建立铲斗斗尖载荷当量模型并获得了斗尖载荷；用雨流计数法统计分段载荷的均值、幅值与频次的关系；对各段载荷频次进行时域扩展，考虑了载荷均值的影响，编制了工作装置8级二维载荷谱和疲劳试验程序加载谱。

1 工作装置载荷测试与信号处理

1.1 载荷测试试验

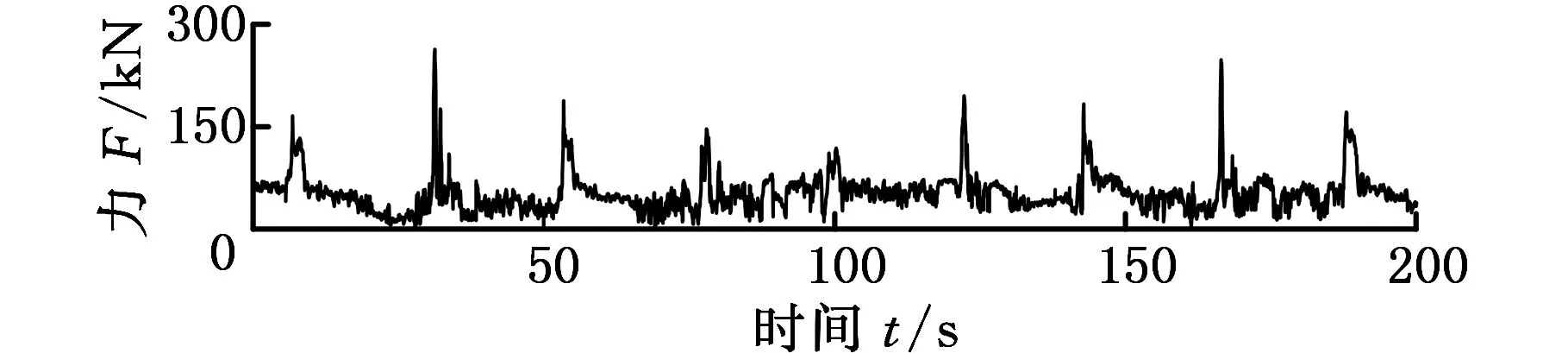
试验样机选择ZL50型装载机，采用销轴传感器测量动臂与铲斗铰接点处载荷，由拉杆拉力确定拉杆与铲斗铰接点处载荷，通过位移传感器测量动臂油缸和摇臂油缸位移，确定工作装置作业姿态。散状物料选择黏土、大石方、小石方和砂子，在国内某工程机械铲运试验场内进行铲装测试。选择L形铲装作业路线，按照作业特点将其分为空载行进、物料铲装、满载运输和物料卸载4段。以效率最高为原则，对4种散状物料进行铲装作业，测得动臂与铲斗铰点力、拉杆力以及油缸位移等时间历程信号。根据传感器标定试验结果，将实测电压与应变信号转换为力信号[9]。黏土物料各测点某段载荷时间历程如图1所示。

(a)动臂与铲斗左侧铰点力时间历程

(b)动臂与铲斗右侧铰点力时间历程

(c)拉杆力时间历程

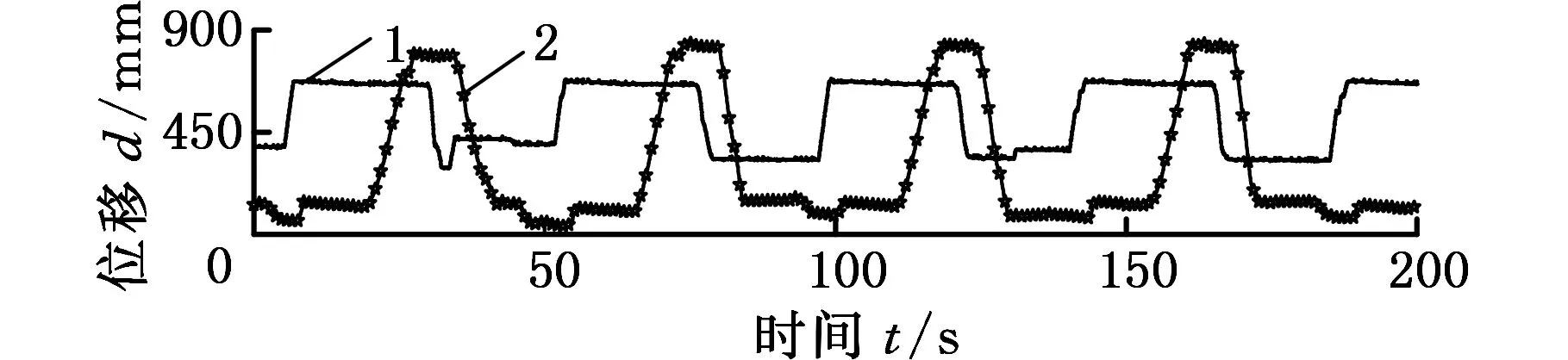
1.摇臂油缸位移 2.动臂油缸位移(d)油缸位移时间历程图1 黏土工况下各测点载荷时间历程Fig.1 Load time history of each measuring point under primary soil condition

由图1可知，各测点载荷随铲装作业呈明显的周期性变化，参照油缸位移变化，动臂与铲斗左右两个铰点力在空载行进和满载运输段呈现平稳变化，且满载运输段载荷均值明显大于空载段载荷均值，而大载荷出现在物料铲装和物料卸载作业段，这与实际作业过程中的载荷变化保持一致，表明所测载荷时间历程能够反映装载机工作装置作业过程中真实的受力特性。

1.2 载荷信号预处理

在铲装作业测试过程中，恶劣的外界工作环境会对测试信号产生一定的干扰，使得载荷时间历程中出现较为明显的异常峰值点。综合运用nCode软件中提供的梯度门限法、幅值门限法和标准方差法进行奇异点的辨别与剔除。随着测试时间的推移，传感器及测试仪器自身的零点漂移使得各测点载荷时间历程波形出现偏移现象，可通过最小二乘法来消除线性趋势项。以动臂与铲斗左铰点载荷为例，剔除奇异值和去零点漂移之后的结果如图2所示。

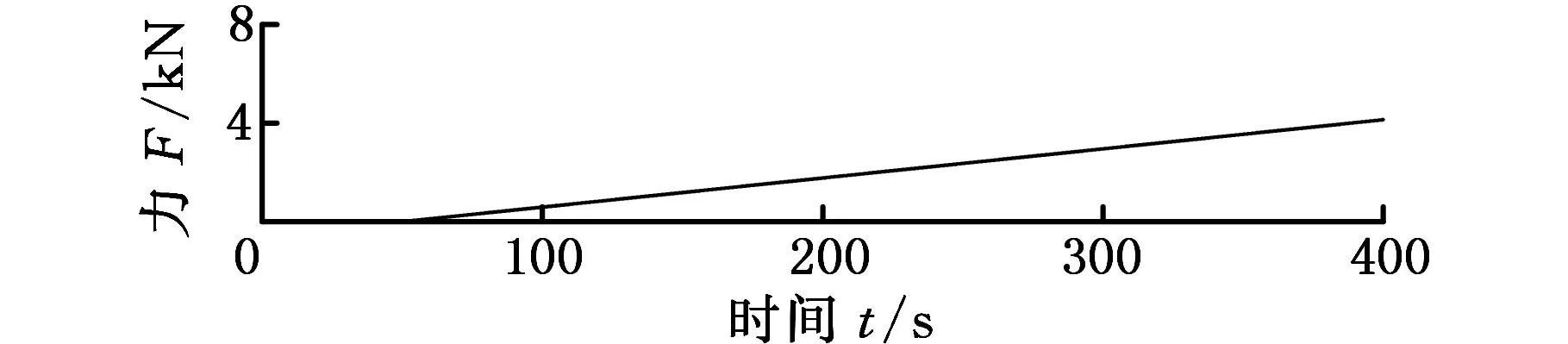
(a)线性趋势项

(b)预处理后左侧铰点力时间历程图2 预处理后左侧铰点载荷时间历程Fig.2 Load time history of left hinge point after pretreatment

对比图1和图2可知，通过预处理后的数据剔除了载荷奇异值，消除了载荷时间历程中的零点漂移现象，保留了反映工作装置受力特性的载荷时间历程数据，为载荷特性分析和载荷谱编制工作打下了基础。

2 斗尖当量载荷与分段

装载机工作装置疲劳可靠性台架试验中，固定工作装置姿态，将所测载荷等效至该姿态下，用作动器施加当量外载荷。工作装置在铲掘物料时刻受到的外载荷最大，根据文献[10]中给出的疲劳试验方案，在工作装置处于铲掘姿态且铲斗处于水平位置时，将铲斗上的3个铰接点的力等效到铲斗中心斗齿的斗尖处。根据动臂油缸和摇臂油缸位移确定工作装置瞬时姿态以及铲斗相对于水平位置时的旋转角度，将动臂与铲斗两个铰点以及拉杆与铲斗铰点处的外载荷转化到该姿态下铲斗铰孔处的载荷[11]，此时铲斗的受力模型如图3所示。

图3 水平姿态下铲斗受力模型Fig.3 The force model of the bucket in the horizontal attitude

图3中，A1、A2分别为铲斗上与动臂连接的左右两个铰孔，B为铲斗上与拉杆连接的铰孔，l1、l2、l3、l4和l5为3个铰孔之间以及铰孔与铲斗中心斗齿斗尖之间的相对距离。根据理论力学[12]知识，以图3中箭头所指方向为正，得到斗尖Fx、Fy、Mx、My和Mz的当量载荷时间历程结果，如图4所示。

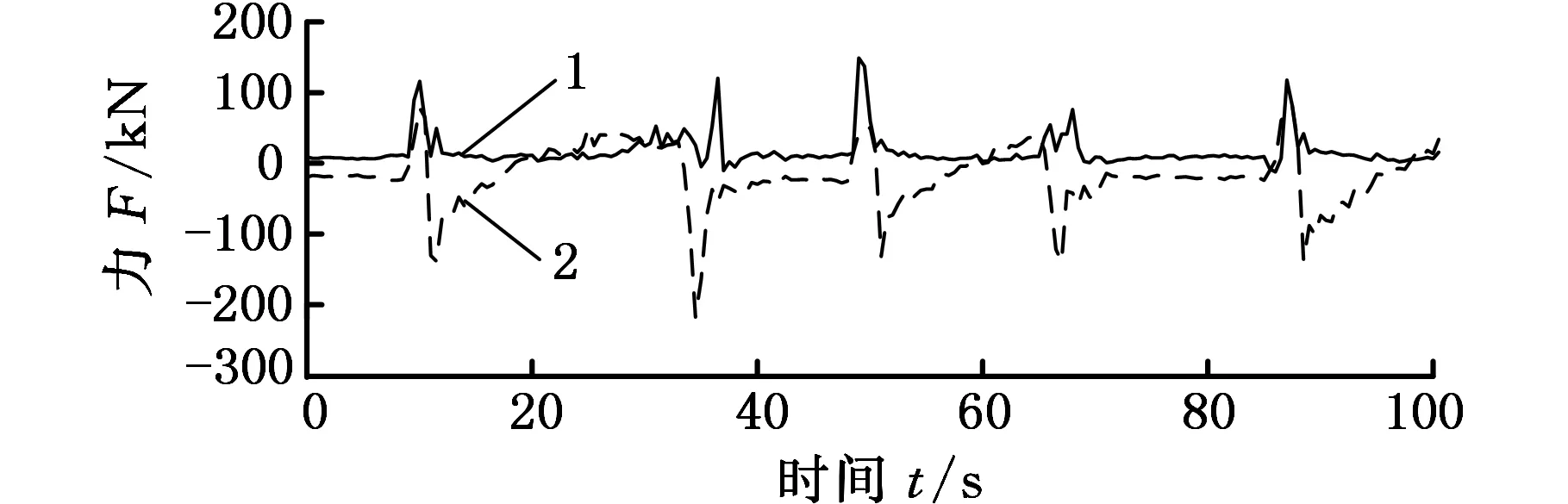
(a)斗尖当量力的时间历程

(b)斗尖当量弯矩的时间历程1.x方向 2.y方向 3.z方向图4 斗尖当量载荷结果Fig.4 Tip equivalent load of the bucket

物料铲装作业过程中，装载机工作装置不断变化姿态，从而实现物料铲装运输及卸料，这种周而复始的作业循环使得被测载荷参数呈现明显周期变化。但是装载机作业环境恶劣多变，工作装置承受的载荷波动较为剧烈，并且不同物料的密度、黏性差异较大，使得工作装置不同作业段的载荷也呈现出明显的分段特性。由此，将一个作业周期内的载荷分为空载行进、物料铲装、满载运输和物料卸载4个作业段，以基本作业段为单位进行载荷平稳性分析和载荷谱的编制。连续铲装作业中，一个作业段的结束即下一作业段的开始，根据载荷变化特性和油缸位移变化，对载荷时间历程进行分段的判别准则见表1。

表1 斗尖载荷分段判别准则

记录所测4种物料每个循环周期中各作业段终止时对应的时刻，即可实现作业段划分。利用轮次法和假设检验法[13]对分段拼接后载荷时间历程进行平稳性和各态历经性检验后可知，各作业段的载荷信号是平稳的和各态历经的，可以取满足统计误差要求的一定数量作业斗数的样本数据来统计推断或代替总体。

3 载荷谱编制

3.1 工况合成与雨流计数

不同工况下工作装置受到的载荷会有明显差异，若以单一物料的铲装试验结果进行统计编谱，会遗漏某些载荷特性，不能准确反映工作装置实际受力变化，需要按照主要典型物料在装载机实际使用过程中的工作比例进行工况合成。统计企业调研结果，在100斗的样本数据中，黏土工况为40斗，大石方工况、小石方工况和砂子工况均为20斗。将4种物料不同作业段的载荷数据按照时间比例进行分段数据合成。选用雨流计数法对斗尖当量载荷时间历程进行统计计数。铲斗斗尖y方向当量载荷在物料铲装作业段的32级雨流计数均值幅值三维柱状图如图5所示。

图5 物料铲装作业段雨流计数结果Fig.5 Rain flow counting results of the material loading operation section

3.2 载荷分布规律

根据雨流计数结果，求出均值幅值联合概率密度函数，分析载荷分布规律。工程实际中，常假设均值概率分布和幅值概率分布分别服从正态分布和威布尔分布[14]。按照费歇定理，在均值、幅值分布相互独立时，两个随机变量近似服从自由度为(r-1)(s-1)的卡方分布χ2，则有

(1)

式中，m为样本容量；r、s分别为均值和幅值的分级数；mi为均值在第i级的频次数；mj为幅值在第j级的频次数；mij为均值在第i级且幅值在第j级的频次数。

卡方分布由正态分布构造而成，自由度很大时，卡方分布近似服从正态分布，自由度为n的卡方分布χ2的上α分位数可由标准正态分布的上α分位数Uα通过下式近似求得：

(2)

(3)

式中，x、y分别为载荷均值和幅值；σ、u分别为正态分布的标准差和均值；γ、β、ε分别为威布尔分布的形状、尺度参数和阈值。

以斗尖y方向物料铲掘段当量载荷雨流计数结果为例，均幅值直方图以及利用线性回归最小二乘法按照正态分布和威布尔分布拟合曲线分别如图6a和图6b所示。

(a)均值频次直方图

(b)幅值频次直方图图6 均值和幅值频次直方图与分布拟合Fig.6 Mean value and amplitude frequency histogram and distribution fitting results

由图6可知，斗尖y方向当量载荷的均值分布的均值估计量为4.539 kN，标准差估计量为48.29 kN；幅值分布的形状参数估计量为1.247，尺度参数估计量为39.58，阈值估计量为5.459。4个作业段的分布参数估计量见表2。

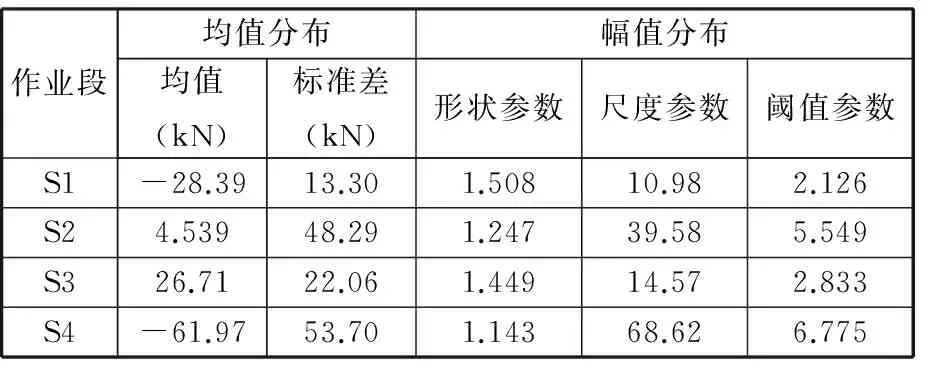
表2 均值幅值分布拟合参数

3.3 二维谱与试验谱编制

100斗样本数据容量有限，不能够代表总体中发生次数较少的大载荷，因此，需要对每一个作业段的载荷累计频次进行扩展，使其达到106次循环，从而再现更加真实的载荷时间历程。累计频次扩展计算公式[15]为

N″η=106Nη/N′

(4)

η=1,2,3,4

式中，N″η为第η个作业段扩展后的载荷累计频次数；Nη为第η个作业段的载荷累计频次数；N′为100斗样本的总累计频次数。

空载、物料铲装、运输和卸载4个作业段扩展后的累计频次数分别为342 731、142 738、421 257和93 038。

由于试验条件及测试样本长度的限制，需要运用统计学理论推断极值载荷。由前文分析可知，斗尖当量载荷的均值和幅值相互独立且分别服从正态分布和三参数威布尔分布，推断出均值和幅值的最大值即可得到载荷极值。由均值幅值联合概率密度函数和极值载荷发生概率P以及标准正态偏差uP，分别得到均值极值Fxmax和幅值极值Fymax的计算公式：

Fxmax=uPσ+u

(5)

(6)

求得均值和幅值的极值后，需要将连续的载荷累计频次曲线转换为易于实现的阶梯型二维载荷谱。将载荷谱分为8级能够准确反映载荷疲劳效应[16]。8级二维载荷谱中，均值区间以均值的最大值为准采用等间隔划分，幅值区间以幅值最大值为基础采用比值系数法进行非等间隔划分，各级比值系数分别为1、0.95、0.85、0.725、0.575、0.425、0.275和0.125。对应第i级均值和第j级幅值区间的载荷循环数Nij由均幅值联合概率密度函数f(x,y)和下式求得：

(7)

式中，τi、τi+1分别为第i级均值载荷的下限和上限；τj、τj+1分别为第j级幅值载荷的下限和上限。

斗尖y方向当量载荷物料铲掘作业段8×8级二维载荷谱见表3。

表3 y方向当量载荷物料铲掘段二维载荷谱

二维载荷谱能够较好地模拟实际载荷，但是由于载荷均值变化的存在，结构件台架试验时却难以实现二维谱的加载，故根据波动中心法，将二维载荷谱转化为均值恒定的一维试验加载谱。按照上述编谱方法，对其他3个作业段中斗尖y方向当量载荷进行编谱。y方向斗尖载荷4个作业段一维试验谱见表4。

表4 y方向斗尖载荷4个作业段一维试验谱

考虑载荷加载顺序的影响[17]，以实际铲装作业过程分段为顺序，在每个作业段内采用低-高-低的顺序采取铲装、运输、卸载和运输分段的方式加载。根据波动中心法，将每一个作业段的载荷均值作为波动中心，再将该作业段的幅值叠加在均值上，按照低-高-低的加载顺序，对各级载荷分10次进行加载即可。装载机工作装置斗尖y方向当量载荷程序加载谱如图7所示。

图7 y方向当量载荷程序加载谱Fig.7 Program loading spectrum of equivalent load in y direction

4 结论

(1)试验测试了真实环境中4种不同物料工况下装载机工作装置销轴和拉杆载荷信号，通过滤波降噪去奇异值等预处理，保留了反映工作装置真实受力特性的载荷时间历程数据。建立了铲斗斗尖载荷当量模型，将铲斗各铰点对作业姿态不断变化的载荷等效为斗尖载荷，此时工作装置作业姿态与斗尖载荷方向相对地面固定，为实现工作装置疲劳台架试验的载荷施加打下了基础。

(2)对斗尖当量载荷进行分段，实现了各作业段载荷的平稳性检验；用雨流计数法统计物料铲装作业段均值、幅值与频次关系，载荷均值频次服从正态分布，载荷幅值频次服从三参数威布尔分布，且载荷均幅值分布相互独立。根据雨流计数和统计结果，对各工作段载荷频次进行时域扩展，实现了8级二维载荷谱的编制；采用波动中心法按照低高低的加载顺序得到了斗尖y方向的疲劳试验程序加载谱，为装载机工作装置台架试验和疲劳寿命预测提供了依据。

[1] 高镇同. 疲劳应用统计学[M]. 北京: 国防工业出版社,1994. GAO Zhentong. Statistics in Fatigue[M]. Beijing: National Defense Industry Press,1994.

[2] LEE Y L, PAN J, HATHAWAY R B, et al. Fatigue Testing and Analysis(Theory and Practice)[M]. Burlington: Elsevier Butterworth-Heinemann,2005.

[3] 万一品, 贾洁, 梁佳, 等. 装载机工作装置结构强度分析与试验研究[J]. 机械强度,2016,38(4):772-776. WAN YiPin, JIA Jie, LIANG Jia, et al. Structural Strength Analysis and Experimental Research for Working Device of Loader[J]. Journal of Mechanical Strength,2016,38(4):772-776.

[4] 闫楚良, 高镇同. 飞机高置信度中值随机疲劳载荷谱的编制原理[J]. 航空学报,2000,21(2):118-123. YAN Chuliang, GAO Zhentong. Compilation Theory of Median Stochastic Fatigue Load-spectrum with High Confidence Level for Airplane[J]. Acta Aeronautica Et Astronautica Sinica,2000,21(2):118-123.

[5] 于佳伟, 郑松林, 赵礼辉, 等. 整车室内道路模拟试验用载荷谱的编制方法研究[J]. 机械工程学报2015,51(14):93-99. YU Weijia, ZHENG Songlin, ZHAO Lihui, et al. Research on Spectrum Development Methodology for Vehicle Indoor Road Simulation Test[J]. Journal of Mechanical Engineering,2015,51(14):93-99.

[6] 张云龙, 诸文农, 殷永光, 等. 装载机驱动桥半轴随机载荷分析及其载荷谱编制方法探讨[J]. 工程机械,1988,19(8):19-23. ZHANG Yunlong, ZHU Wennong, YIN Yongguang, et al. Random Load Analysis of Drive Axle Shaft in Shovel Loader and a Study of Load Spectrum Preparation[J]. Construction Machinery and Equipment,1988,19(8):19-23.

[7] 张云龙, 诸文农, 许纯新. 装载机传动系载荷样本长度的确定[J]. 工程机械,1994,25(6):16-19. ZHANG Yunlong, ZHU Wennong, XU Chunxin. Determination of Load Sample Length for Loader Driveline[J]. Construction Machinery and Equipment, 1994,25(6):16-19.

[8] 高云凯, 徐成民, 方剑光. 车身台架疲劳试验程序载荷谱研究[J]. 机械工程学报,2014,50(4):92-98. GAO Yunkai, XU Chengmin, FANG Jianguang. Study on the Programed Load Spectrum of the Body Fatigue Bench Test[J]. Journal of Mechanical Engineering,2014,50(4):92-98.

[9] 万一品, 宋绪丁, 郁录平, 等.装载机工作装置销轴载荷测试方法与试验研究[J].机械强度,2017,39(1):26-32. WAN Yipin, SONG Xuding, YU Luping, et al. Study on load Measuring Method and Test of the Pin-shaft in Loader Working Device[J].Journal of Mechanical Strength,2017,39(1):26-32.

[10] 中华人民共和国机械电子工业部.JB/T5958-1991装载机工作装置疲劳试验方法[S]. 北京: 机械科学研究院出版社,1992. Ministry of Machinery and Electronics Industry of the People’s Republic of China.JB/T 5958-1991 Fatigue Test Method of Loader Working Device[S]. Beijing: Mechanical Science Research Institute Press,1992.

[11] 万一品, 宋绪丁, 郁录平, 等. 装载机工作装置斗尖载荷当量模型与试验[J]. 长安大学学报(自然科学版),2017,37(3):119-126. WAN Yipin, SONG Xuding, YU Luping, et al. Bucket Tip Load Equivalent Model and Experiment on Loader Working Device [J]. Journal of Chang’an University(Natural Science Edition),2017,37(3):119-126.

[12] 哈尔滨工业大学理论力学教研室.理论力学[M]. 北京: 高等教育出版社,2002. Department of Theoretical Mechanics, Harbin Institute of Technology.Theoretical Mechanics[M]. Beijing: Higher Education Press,2002.

[13] 王强, 苏成. 公路桥梁随机车队的平稳性和各态历经性 [J], 华南理工大学学报(自然科学版),2015,43(10):8-15. WANG Qiang, SU Cheng.Stationarity and Ergodicity of Random Motorcade on Highway Bridge[J]. Journal of South China University of Technology( Natural Science Edition),2015,43(10):8-15.

[14] 张英爽, 王国强, 王继新, 等. 工程车辆传动系载荷谱编制方法[J]. 农业工程学报,2011,27(4):179-183. ZHANG Yingshuang, WANG Guoqiang, WANG Jixin, et al. Compilation Method of Power Train Load Spectrum of Engineering Vehicle[J]. Transactions of the CSAE,2011,27(4):179-183.

[15] 刘永臣, 常绿, 孙丽. 轮式装载机传动系载荷谱编制方法研究[J]. 中国机械工程,2012,23(12):1412-1416. LIU Yongchen, CHANG Lü, SUN Li. A Method of Compiling Load Spectrum on Wheel Loader Transmission[J]. China Mechanical Engineering,2012,23(12):1412-1416.

[16] CONOVER J C, JAECKLH R, KIPPOLA W J. Simulation of Field Loading in Fatigue Texting[J]. Journal of Terramechanics,1996,3(3):101-102.

[17] 王旭亮, 聂宏. 考虑载荷加载顺序的模糊Miner 理论研究[J]. 中国机械工程,2008,19(22):2725-2728. WANG Xuliang, NIE Hong.Study on Fuzzy Miner’s Rule Considering Load Sequence[J]. China Mechanical Engineering,2008,19(22):2725-2728.

(编辑 陈 勇)

Compilation Method of Fatigue Experimental Load Spectrum of Loader Working Devices

WAN Yipin1SONG Xuding1YUAN Zhengwen2YU Luping1

1.Key Laboratory of Road Construction Technology & Equipment of Chang’an University,Ministry of Education, Xi’an,710064 2.Engineering Machinery Research Institute of Xuzhou Construction Machinery Group,Xuzhou,Jiangsu,221004

In order to study the fatigue performance of the loader working devices, a method was proposed considering the load mean characteristics for the preparation of load spectrum of fatigue test program. The loads of the pin in 4 typical material shovel loading operations were collected, and the pin loads were converted to equivalent loads at the tip of the bucket. According to the load characteristics, each operation period was divided into 4 sections, which were no load transportation, shovel digging operation, heavy load transportation and unloading operation. The rain flow counting method was adopted to analyze the mean value distributions and amplitude distributions of the 4 sectional loads. The results show that the distributions of load mean and amplitude are independent and obey normal distribution and Weibull distribution with three-parameters respectively. Frequencies were extrapolated and synthesized and the load spectrum of the 8 stage load spectrum and the variable mean fatigue test program were worked out according to the mean amplitude probability distribution function and the wave center method. The method and results of load spectrum compilation provide references for fatigue life prediction and reliability bench test of the loader working devices.

loader; working device; tip equivalent load; load spectrum; fatigue experiment

2016-10-10

国家科技支撑计划资助项目(2015BAF07B02);中央高校基本科研业务费资助项目(310825175009,310825163407)

TH214.3

10.3969/j.issn.1004-132X.2017.15.007

万一品，男，1988年生。长安大学工程机械学院博士研究生。研究方向为工程机械结构载荷测试与疲劳性能。E-mail: wyipin@chd.edu.cn。宋绪丁(通信作者)，男，1963年生。长安大学工程机械学院教授、博士研究生导师。员征文，男，1986年生。徐工集团江苏徐州工程机械研究院工程师。郁录平，男，1957年生。长安大学工程机械学院教授。