基于混合博弈的产品多学科柔性设计决策
2017-08-31李廖平
陈 亮 李廖平
福州大学机械工程及自动化学院,福州,350116
基于混合博弈的产品多学科柔性设计决策
陈 亮 李廖平
福州大学机械工程及自动化学院,福州,350116
针对产品多学科多目标的设计决策问题,给出了一种融合博弈论和柔性机制进行建模和求解的方法。通过混合博弈来表征学科之间及目标之间的耦合关系,提出了混合博弈模型框架及求解方法。考虑到不确定性和变化的影响,为使产品设计决策具有柔性,引入性能水平满意度函数来柔性表达设计要求,并寻求设计变量的柔性范围解来替代固定值的点解,从而增加产品的柔性;柔性范围解处于可行设计空间内,使各学科性能处于满意水平并靠近期望值,且具有较好的稳定性。利用概率分布对相应的性能变化进行建模,引入设计偏好指数对柔性设计方案进行评价。最后通过减速器算例的设计来验证该方法的可行性和有效性。
多学科设计;柔性决策;博弈;偏好指数;减速器
0 引言
复杂产品设计往往涉及多个学科领域,需要综合考虑多学科间的相互作用和协同效应,进行协同设计决策来获得各方满意的设计方案。由于多学科间存在着复杂的耦合关系,学科间相互制约,甚至存在矛盾冲突,存在信息的不确定性,使得设计方案的确定十分困难,因此,复杂产品设计决策中的多学科耦合分析是设计的关键,如何有效地处理学科间的耦合关系,获得各学科均满意且综合性能好的设计方案是复杂产品设计开发的核心问题之一。
多学科设计优化(multidisciplinary design optimization ,MDO)是常用的方法之一,多学科设计优化算法可以分为单级算法和多级算法[1]。单级算法(如单学科可行法和多学科可行法)[2]将所有的决策优化集中到一个优化器中,其他学科只在需要的时候提供学科分析,它是一种集中式的决策模型,问题复杂时难以求解。多级算法如并行子空间优化(concurrent subspace optimization,CSSO)算法[3]和协同优化(collaborative optimization, CO)算法[4]克服了单级算法的缺点,将系统的优化设计问题分为两级:一个系统级和并行的多个学科级。由于系统层和学科层之间需要不断地迭代,当问题维数高时求解困难,计算复杂性和组织复杂性难以消除,收敛性也难以保证。另外,子系统间复杂的耦合关系会带来设计信息的不确定性,因为各子系统只能控制整个系统的部分设计变量,它所需的由其他子系统控制的设计变量就成为其未知和不确定的耦合变量。MDO方法通过一致性约束(如协同优化等)来考虑子系统间的相互耦合影响,但对耦合变量的处理过于复杂,会消耗大量的分析迭代次数,忽略了学科设计间的策略互动与动态调整过程[5-6]。为此,复杂产品的设计需要对子系统间的交互作用进行建模,并对子系统间的耦合所导致的信息不确定性进行分析和处理,以减少子系统之间的耦合,并寻求提高系统质量和稳定性的鲁棒解,提高系统的整体性能。
博弈论在表达工程团队间的交互时是有效的[7-8],可有效应用于产品设计中[9-10]。利用均匀设计试验法能确定机械产品多目标优化设计博弈分析中博弈方的策略集[11]。利用博弈理论进行产品设计可避免人为确定各目标权重或建立特别综合评价函数带来的影响[12],博弈方遵循博弈过程中的理性法则进行竞争与合作,动态协调最终达到均衡点,克服了MDO方法忽略学科间策略互动与动态调整的不足。另外,通过去除系统层团队,给各学科团队赋予自治权,能够减少迭代次数,降低计算和组织复杂性。
复杂产品设计是一个渐进过程,存在很多不确定性因素,为了减少设计迭代反复,获得综合性能好、抵御不确定因素干扰和适应变化的设计解,需要在设计中融入柔性[13]。柔性是一种适应不断变化的能力[14],为了增加产品的柔性,需要在产品设计中考虑影响产品设计的变化因素,如设计要求的变化、产品设计参数的变化等,并采用有效的方法和机制处理这些变化因素,以保证在这些变化情况下仍保持设计解的可行性,以及性能水平的满意度和稳定性。针对上述问题,本文采用混合博弈对多学科交互设计决策过程进行分析,建立多学科设计决策的博弈框架,通过引入柔性机制和设计偏好指数来考虑不确定性的影响,处理各博弈方的策略选择和进行各博弈方之间的收益均衡,在此基础上,给出了一种复杂产品多学科柔性设计决策博弈模型,通过求解该模型获得综合性能高且各方满意的解,并以减速器算例来说明该方法的可行性和有效性。
1 多学科设计问题的博弈分析框架
复杂产品设计涉及多个学科,而各个学科通常又有多个目标。本文采用博弈论的方法处理产品多学科多目标设计问题,将决策者设置为局外人,把各个学科或各个目标作为博弈方。通过计算设计变量对各个学科的影响因子,根据设计变量与学科的相关性进行模糊聚类划分,将设计变量分配给与之关系较为密切的各个学科和目标。设计变量方案集合是博弈策略集,一种策略对应博弈方的一种收益。通过博弈的理性法则,自然引导各博弈方的竞争与合作,最终达到均衡点,得到对应多学科设计问题的博弈均衡解。这种基于博弈理性的均衡解具有较好的稳定性与合理性,考虑了多个学科多个目标之间的相互影响和冲突,实现了综合优化和均衡协调。决策者这个局外人则根据自己的偏好,从博弈解中选取其满意解。根据学科间的关系及彼此信息了解情况,学科间可以是合作博弈、非合作博弈或领导-随从博弈。学科下的优化目标隶属于学科,与学科之间的关系是领导-随从关系,用领导-随从博弈来分析和建模,而学科下各优化目标之间视为合作关系,采用合作博弈来分析和建模,相应的混合博弈分析框架如图1所示。

图1 博弈分析框架Fig.1 Game framework
1.1 合作博弈(Pareto博弈)
在合作博弈中,各博弈方彼此间共享信息,以集体理性为基础,以追求集体利益为目标,共同遵守某个具有合作性的约束力协议,通过协商和合作来获取联盟的整体最优利益。通过合作获取的联盟整体收益将按照一定的规则进行分配,基本原则是保证每个博弈方所得不少于它们单独行动(脱离联盟,不合作)而获得的利益,其结果对各博弈方来说不一定是最优结果,但一定是可以接受的相对较优的结果,即合作博弈结果是一个Pareto最优解。
定义合作博弈的决策模型为
(1)

由于各设计目标之间的数量级可能存在差异,为了避免数量级相差太大而对设计结果产生影响,需要对各个设计目标进行归一化处理,将各个博弈方置于同一水平,以消除数量级的影响。归一化处理后合作博弈的决策模型为
(2)

1.2 非合作博弈(Nash博弈)
非合作博弈发生于由于组织、信息或过程等障碍而相互隔离的情形,各博弈方之间信息不共享,各自决策,以个体理性为基础,各博弈方选择一种对自己有益的策略,而不考虑其他博弈方的得失,也不考虑集体利益,以自身利益最大为目标进行博弈,获得Nash均衡解,在均衡点位置任何博弈方都不愿意改变自己的策略选择,否则将会降低自身的得益,所以Nash均衡解是一个稳定的收敛解,但不一定是 Pareto 最优的。
本文采用Nash遗传算法进行非合作博弈求解。每个博弈方被分配一个种群和一个目标函数进行优化。每个博弈方只能修改分配给它的设计变量,通过标准遗传算子执行操作。在每个时间点(即一代)后,博弈方和其他博弈方交换它们的最优值,算法最终收敛于Nash均衡解。具体过程如图2所示,假设有两博弈方P1和P2,博弈方P1控制变量x,博弈方P2控制变量y。分别给每个博弈方分配一个种群,开始时,初始化两种群,通过标准遗传算子,两个种群在各自种群内优化。需要注意的是,种群P1优化时,x是变量,y为种群P2上代优化后的最优解,是一个确定的量;同理,种群P2优化时,y是变量,x为种群P1上代优化后的最优解,是一个确定的量。当优化达到终止条件时,达到Nash均衡,否则继续优化。与并行遗传算法PGA中每个子种群使用相同的准则不同,Nash遗传算法则中各子种群使用不同的准则,因此有均衡的概念。

图2 Nash遗传算法Fig.2 Nash genetic algorithm
1.3 领导-随从博弈
领导-随从博弈是一种考虑了博弈方设计决策顺序的博弈模型,是Nash博弈的一个特例。领导-随从博弈分领导博弈方和随从博弈方,两方的地位不同,领导博弈方在博弈中取得较高的决策权。该博弈是由领导博弈方在假定随从博弈方理性行为的情况下做出自己的设计决策,随后随从博弈方再根据领导博弈方的决策做出自己的决策,并且随从博弈方的决策要与领导博弈方的决策协调一致,尽量靠近领导博弈方的决策。第i个随从博弈方的博弈模型为
(3)
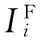
1.4 混合博弈
混合博弈是指在一个博弈过程中同时拥有以上三种博弈中的两种及两种以上的博弈形式,图1所示的多学科博弈框架即混合博弈,其中涉及合作博弈、非合作博弈和领导-随从博弈三种博弈方式,其求解过程如图3所示。

图3 混合博弈求解算法Fig.3 Mixed game algorithm
(1)各学科之间先进行非合作博弈(或合作博弈、领导-随从博弈,根据学科间的关系来确定),得到Nash均衡解(或Pareto解)。
(2)各学科作为领导方,其下各子目标为随从方,进行领导-随从博弈。领导方的解为步骤(1)中的Nash均衡解(或Pareto解),由领导方的解可求得各随从方的期望值,然后随从方进行设计决策获得其随从解。
(3)各子目标间进行合作博弈得到Pareto前沿,再从中选取与步骤(1)中的解最接近的一个解。
2 产品柔性设计决策
为了适应不确定性和变化的条件,产品设计决策需要具有柔性。考虑影响产品设计要求的变化,应寻求设计要求的柔性表述,替代传统的设计要求被指定为刚性约束或目标(表现为一个精确的数值)的情形,允许设计性能要求是变化值,不同的性能水平满意度不同,通过引入性能水平的满意度函数S(y)来衡量不同性能水平的满意度,其定义为满意度S与性能水平y之间关系的函数。考虑到性能水平离期望值越远,设计者对目标的满意度呈加速下降的趋势,本文使用二次函数来替代传统的刚性精确值(如图4为小好型(STB),根据设计问题类型,也可以是大好型(LTB)或中间好型(CTB))。函数值在0~1之间,1代表完全满意,表示设计方案被认为是完全可接受或满意的;函数值为0代表完全不满意,表示设计方案被认为是不可接受的,这种方法与传统优化方法相比更加具有柔性。
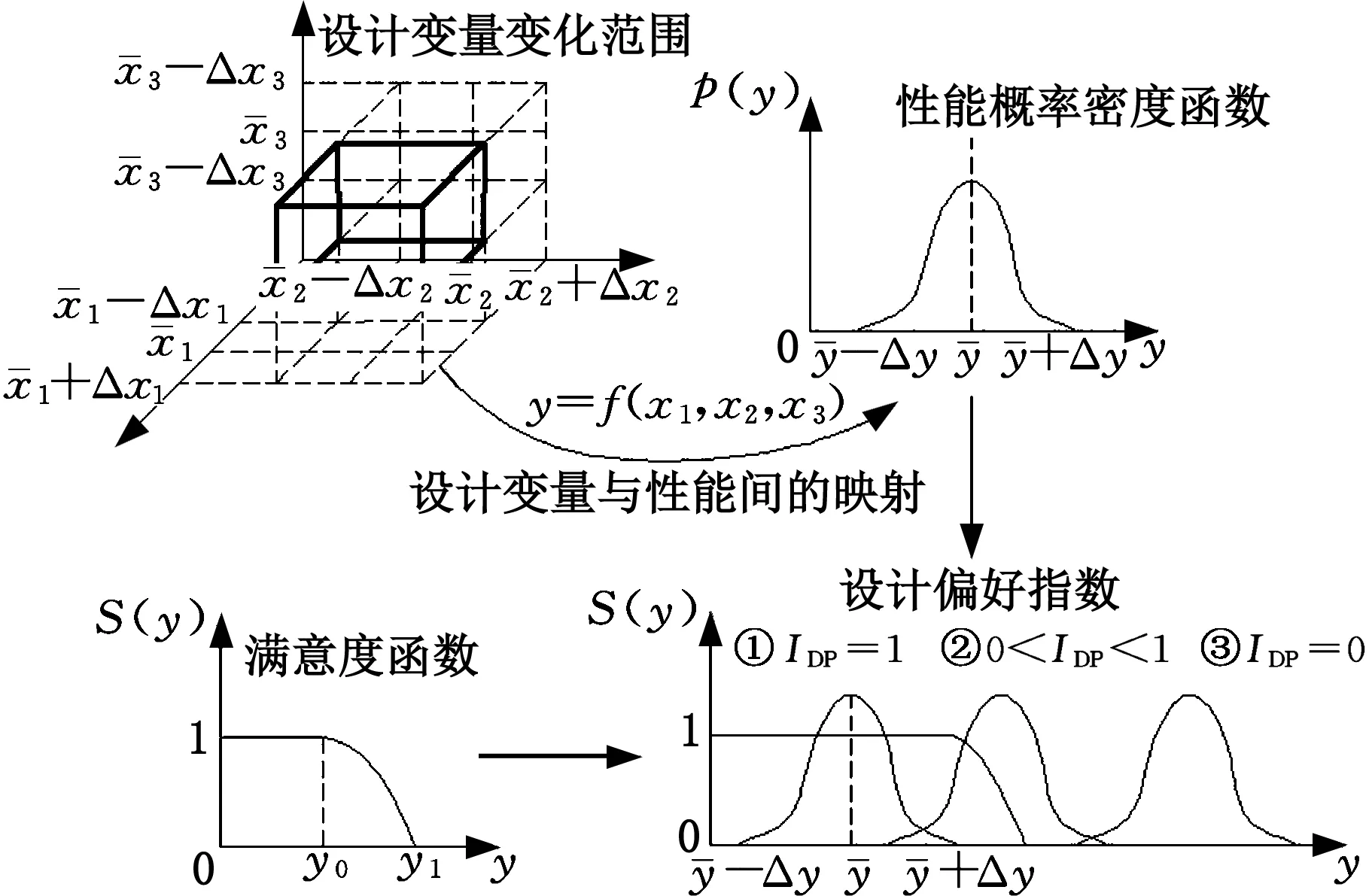
图4 柔性设计决策Fig.4 Flexible design and decision

为了对设计进行评价,引入设计偏好指数(design preference index ,DPI)IDP[15],其定义为设计变化范围内性能满意度函数S(y)的数学期望:
(4)
当设计变量在设计解范围内变化时,引起设计性能和性能满意度在相应范围内变化,IDP的含义是衡量和评价在这种变化下对设计要求的总体满足情况,即对本文给出的柔性设计方案进行衡量和评价的一种指标。IDP值越大,表示性能分布函数和满意度函数的重合度越大。IDP为1时意味着在这种变化下设计能完全满足设计要求,即在设计解范围内的点均是可行的,且相应的性能水平具有高的满意度,这是理想情况,显然,使IDP尽量接近1是所期望的。

(5)
然而,IDP值为1在某些情况下是不能达到的,如设计方案②、③所示。
基于上述分析,将设计决策模型中的目标函数定义为设计能力指数IDP值与1之差,给设计变量xi以变化范围Δxi,并增加约束Δxi≥Δximin,这是为了确保设计解的最小柔性,若没有这个约束,设计变量Δxi范围将会趋近于0,设计解退化为常规的单点解,性能水平则成为确定值。增加约束Δyi≤yimax,可限定性能的最大变化,使性能保持必要的稳定性。由此得到柔性设计决策模型:
设计变量:x,Δxi
设计目标:min 1-IDPi;i=1,2,…,m

设计约束:Δxi≥Δximin,i=1,2,…,n
Δyi≤Δyimax,i=1,2,…,m
边界范围:
lbj≤xj≤ubj
通过求解该模型,可获得设计变量柔性范围解,它处于可行设计空间内,且在此范围解集内,各学科性能处于满意水平并尽可能靠近期望值,而且具有较好的稳定性。
3 实例分析
齿轮减速器问题[16](speed reducer problem,SRP)被NASA认为是检验MDO方法性能的十大标准算例之一。该问题包含齿轮设计和轴设计两部分,目标是在满足齿轮的弯曲应力、接触应力以及轴的位移和应力等约束条件下使减速器的质量最小。其数学表达如下:

g7=x2x3/40-1.0≤0
g8=5x2/x1-1.0≤0
g9=x1/(12x2)-1.0≤0
g10=(1.5x6+1.9)/x4-1.0≤0
g11=(1.1x7+1.9)/x5-1.0≤0
2.6≤x1≤3.6 0.7≤x2≤0.8
17≤x3≤28 7.3≤x4≤8.3
7.3≤x5≤8.3 2.9≤x6≤3.9 5.0≤x7≤5.5
式中,x1为齿宽;x2为齿轮模数;x3为小齿轮齿数;x4为轴1上轴承间距;x5为轴2上轴承间距;x6为轴1直径;x7为轴2直径;g1为齿轮轮齿最大弯曲应力约束;g2为齿轮轮齿最大接触应力约束;g3为轴1横向最大挠度约束;g4为轴2横向最大挠度约束;g5为轴1最大应力约束;g6为轴2最大应力约束;g7、g8、g9为尺寸和空间约束;g10为轴1尺寸经验设计约束;g11为轴2尺寸经验设计约束。
在MDO中,将学科定义为系统中本身相对独立、相互之间又有数据交换关系的基本模块,又称作子系统或子空间[17]。将减速器设计问题分解为两个子系统和三个目标的设计优化问题,子系统1负责齿轮设计,子系统2负责轴设计,见表1。
3.1 单目标最优解
对各目标进行优化得到相应的单目标最优解:

表1 学科子系统划分
3.2 策略集划分
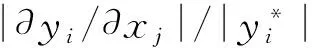

表2 各目标偏导数情况
可得出各变量对三个目标的影响因子:Δ1={1,0,0};Δ2={1,0,0};Δ3={1,0,0};Δ4={0,1,0};Δ5={0,0,1};Δ6={0,1,0};Δ7={0,0,1}。然后通过计算相似度,得到模糊相似矩阵;再利用传递闭包法求得具有传递性的模糊关系矩阵;最后根据实际情况,选取合适阈值,得到相应分类,确定各博弈方的策略集,限于篇幅,不再赘述,可参见相应模糊聚类分析的文献,最终获得的策略集划分结果为:{x1,x2,x3}隶属于y1;{x4,x6}隶属于y2;{x5,x7}隶属于y3。
3.3 多学科混合博弈模型框架的建立
建立图5所示的减速器混合博弈模型框架,齿轮设计子系统和轴设计子系统间进行Nash博弈, 轴设计子系统下的轴1设计和轴2设计子目标间进行合作博弈。为了便于比较,分为不使用设计偏好指数和使用设计偏好指数两种情况进行分析。

图5 减速器博弈模型框架Fig.5 Game model of speed reducer
3.3.1 不使用设计偏好指数


(3)合作博弈。建立合作博弈方1(轴1)模型和合作博弈方2(轴2)模型,轴1、轴2设计处于同一数量级水平,进行归一化处理,确定合作博弈决策模型。
(4)求解结果。基于前述的混合博弈求解算法,设定ε=0.01,N=100进行求解,迭代56次得到混合博弈结果:
x*=
{3.5047,0.7,17.0174,7.3016,7.7558,3.3526,5.2872}
y1=1380.8y2=346.213y3=1275.4
3.3.2 使用设计偏好指数
(1)满意度函数的设定。各个学科子系统满意度函数是根据设计者的经验和偏好来确定的,设定减速器各学科子系统的满意度函数如图6所示。

图6 满意度函数Fig.6 Satisfaction function

i=1,2,3
S(y1)=
(3)非合作博弈模型。
Nash博弈方1模型:
Δxi≥0.1xiΔyi≤0.2yi
Nash博弈方2模型:
(4)领导随从博弈模型。
领导博弈方模型:
随从博弈方1模型:
随从博弈方2模型:
(5)合作博弈模型。
合作博弈方1模型:
合作博弈方2模型:
合作博弈决策模型:
s.t.gi(x)≤0i=1,2,…,11

(6)求解。设定ε=0.01,N=100进行求解,迭代78次后得到混合博弈柔性结果:
x={3.5208±0.3291,0.7024±0.0722,17.014±2.7187,
7.4671±0.7774,7.7491±0.8267,3.3495±0.3332,
5.2890±0.5409}
y1=1396.2±594.58y2= 346.77±97.184
y3=1276.5±374.66


表3 结果对比
4 结语
本文基于博弈论对多学科多目标交互设计决策过程进行分析,通过混合博弈来建立学科及目标之间的耦合关系模型, 提出了混合博弈模型框架及求解方法。为了使设计具有柔性以适应不确定性和变化,采用二次型满意度函数来柔性表达设计要求,另外以设计变量的范围解来替代点解,从而使得设计解具有适应变化的柔性。用概率分布密度函数反映性能变化,并用设计偏好指数对设计方案进行评价。实例运行结果表明,本文方法是可行和有效的,柔性范围解处于可行设计空间内,各学科目标性能处于满意水平并靠近期望值,而且具有较好的稳定性。对于复杂产品多学科多目标设计决策问题,得到综合性能好且能适应不确定性和变化因素影响的范围解比追求单纯的最优解更有实际意义,所以本文方法具有较好的指导意义,并且获得的柔性范围解可作为进一步详细设计的基础。
[1] 刘克龙,姚卫星,余雄庆.几种新型多学科设计优化算法及比较[J].计算机集成制造系统,2007,13(2):209-216. LIU Kelong , YAO Weixing, YU Xiongqing. Some New Algorithms for Multidisciplinary Design Optimization and Their Comparison [J].Computer Integrated Manufacture Systems,2007,13(2):209-216.
[2] HAFTKA R T , SOBIESZCZANSKI-SOBIESKI J, PADULA S L . On Options for Interdisciplinary Analysis and Design Optimization[J]. Structural and Multidisciplinary Optimization,1992,4(2):65-74.
[3] SELLAR R S, BATILL S M, RENAUD J E.Response Surface Based,Concurrent Subspace Optimization for Multidisciplinary System Design[C]//34th AIAA Aerospace Sciences Meeting and Exhibit.Reno, 1996,AIAA-1996-0714.
[4] SOBIESKI I P, KROO I M. Collaborative Optimization Using Response Surface Estimation[J]. AIAA Journal, 2000,38(10):1931-1938.
[5] 马明旭,王承恩,张嘉易,等. 复杂产品多学科设计优化技术[J].机械工程学报,2008,44(6):15-26. MA Mingxu, WANG Chengen, ZHANG Jiayi,et al.Multidisciplinary Design Optimization for Complex Product Review[J].Journal of Mechanical Engineering,2008,44(6):15-26.
[6] 叶国青,姜江,陈森,等.武器装备体系设计问题求解框架与优化方法[J].系统工程与电子技术, 2012,34(11):2256-2263. YE Guoqing,JIANG Jiang,CHEN Sen,et al.Design Optimization of Weapon System of Systems Based on Collaborative Multidisciplinary Decision-making[J].System Engineer and Electronics,2012,34(11):2256-2263.
[7] LEWIS K, MISTREE F. Modeling Interactions in Multidisciplinary Design: a Game Theoretic Approach[J]. AIAA Journal,1997,35(8):1387-1392.
[8] Shun T K. A Game-theoretic Model of Collaboration in Engineering Design[J].Journal of Mechanical Design, 2010,132(5):051005-1-9.
[9] DHINGRA A K, RAO S S. A Cooperative Fuzzy Game Theoretic Approach to Multiple Objective Design Optimization[J].European Journal of Operational Research,1995,83(3):547-567.
[10] LIANG Z X, YAN L, SHANG J Z.Ship Cabin Layout Design Using Game Theory[J]. Journal of Marine Science and Technology, 2008,13(4):446-454.
[11] 陈加明,宋小文,徐浩.结合模糊聚类和合作竞争博弈的优化方法[J].中国机械工程,2015,26(16):2179-2182. CHEN Jiaming, SONG Xiaowen, XU Hao.Optimization Method Based on Fuzzy Clustering and Cooperative Competition Game[J]. China Mechanical Engineering,2015,26(16):2179-2182.
[12] 郑丞,金隼,来新民,等.基于非合作博弈的公差分配优化[J].机械工程学报,2009,45(10):159-165. ZHENG Cheng, JIN Sun, LAI Xinmin,et al.Tolerance Allocation Optimization Based on Non-cooperative Game Analysis[J].Journal of Mechanical Engineering,2009,45(10):159-165.
[13] SIMPSON T W, ROSEN D, ALLEN J K, et al. Metrics for Assessing Design Freedom and Information Certainty in the Early Stages of Design[J]. Journal of Mechanical Design, 1998,120(4):628-635.
[14] JOSEPH H S, DANIEL E H, DAVA J N. Flexibility in System Design and Implications for Aerospace Systems[J]. Acta Astronautica,2003,53(12):927-944.
[15] CHEN W, YUAN C. A Probabilistic-based Design Model for Achieving Flexibility in Design[J]. Journal of Mechanical Design,1999,121(1):77-83.
[16] PADULA S L, ALEXANDROV N, GREEN L L. MDO Test Suite at NASA Langley Research Center[C]//Proceedings of the 6th NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization.Bellevue, 1996:AIAA-1996-4028.
[17] 王振国,陈小前,罗文彩,等.飞行器多学科设计优化理论与应用研究[M].北京:国防工业出版社,2006. WANG Zhenguo, CHEN Xiaoqian, LUO Wencai,et al.Research on the Theory and Application of Multidisciplinary Design Optimization of Flight Vehicles[M].Beijing: National Defend Industry Press,2006.
[18] LI X, LIU C, LI W, et al. An Alternative Formulation of Collaborative Optimization Based on Geometric Analysis[J].Journal of Mechanical Design,2011,133(5):623-635.
(编辑 陈 勇)
Multidisciplinary Flexible Design and Decision Based on Mixed Game
CHEN Liang LI Liaoping
College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou ,350116
For the problems of multidisciplinary and multiobjective design and decision, a novel method was given using game theory and flexibility mechanism to model and solve the problems. The coupling relations among disciplines or targets were presented by mixed game, and the mixed game model framework and the corresponding solving methods were proposed. Considering the influences of uncertainty and changes, in order to make the design and decision be flexible, the satisfaction function of performance was introduced to express the flexible design requirements, and the flexible range solutions of design variables were sought rather than a point solution to increase product flexibility. The flexible range solutions were in the feasible design spaces, where every discipline’s performances were satisfactory and close to the expected values and had good stability. Probabilistic representation was used to model the corresponding design performance changes, and design preference index (DPI) was introduced to evaluate the flexible design. Finally, a gear reducer design example was given to verify the feasibility and effectiveness of the proposed method.
multidisciplinary design; flexibility decision; game; preference index; reducer
2016-09-01
国家自然科学基金资助项目(50875049);福建省自然科学基金资助项目(2014J01184)
TH122
10.3969/j.issn.1004-132X.2017.15.014
陈 亮,男,1963年生。福州大学机械工程及自动化学院教授、博士。主要研究方向为多学科协同设计、优化和决策,现代设计理论和方法等。E-mail: chenliang@fzu.edu.cn。李廖平,男,1989年生。福州大学机械工程及自动化学院硕士研究生。
