基于盲数理论的萤火虫神经网络失效征候结构可靠度预测

董 青 徐格宁

太原科技大学机械工程学院，太原，030024

基于盲数理论的萤火虫神经网络失效征候结构可靠度预测

董 青 徐格宁

太原科技大学机械工程学院，太原，030024

在任意可行性工况下，针对大型臂架失效征候结构的载荷效应与抗力的多种不确定因素导致结构可靠度难以确定的问题，通过构建盲数失效征候结构可靠度模型(BNFSSRM)、串行式萤火虫神经网络预测模型——缺陷结构远场应力预测子模型(STFNN-DSSSPSM)与缺陷结构可靠度预测子模型(STFNN-DSRPSM)串联，提出了基于盲数理论的萤火虫神经网络失效征候结构可靠度预测方法。以应力-强度干涉模型为基础，萤火虫神经网络为预测方法，根据裂纹失稳扩展准则，将不确定性问题盲数化的思想引入裂纹强度因子与断裂韧性的干涉模型，通过试验仿真与STFNN-DSSSPSM，得到典型工况下裂纹缺陷结构的可靠度；再以此为扩展样本的目标输出、裂纹扩展尺寸为扩展样本的输入，通过BNFSSRM、STFNN-DSRPSM，实时预测不同工况下缺陷结构的可靠度，评估抵抗失效的能力以及不同工况退出可行性工况域的先后顺序。以QY130流动式起重机再制造臂架结构为例，验证了该方法的有效性，为结构再制造准入期实时判断以及再制造方案的选择提供了理论指导。

盲数理论; 失效征候; 裂纹缺陷; 萤火虫神经网络

0 引言

结构失效征候是指结构缺陷并未造成失效事故的发生，但使结构安全存在潜在隐患，即失效事故发生的征兆。宏观裂纹这一特定失效征候的存在对工程机械承载结构的安全使用造成严重威胁。据不完全统计，由裂纹缺陷引起的事故损失每年可达数千亿元。实际环境中，由于经费不足、维修受限、维修无效等原因，导致承载结构存在严重裂纹缺陷的工程机械产品仍服役于作业一线，给安全生产带来了很大的隐患。由此，失效征候承载结构安全预测已成为工程机械再制造领域迫切需要解决的关键问题。

使用、检测、维修、环境等因素的随机性，导致缺陷结构存在大量不确定性因素，包括模糊不确定、随机不确定、认知不确定等，而这些不确定性因素反过来会影响结构安全可靠性。目前，由不确定性因素引起的产品可靠性问题引起了国内外学者的广泛关注。文献[1]以盲数理论及不确定性理论为基础，建立了基于盲数理论的机械结构时变可靠性模型。文献[2]运用未确知理论中盲数的基本概念和运算规则，建立了车架盲数强度应力可靠度模型。文献[3]用盲数理论描述机械零件的强度和受载后的应力变化，采用应力-强度干涉模型建立机械零件的可靠性优化设计模型，实现基于盲数理论的机械零件强度可靠性优化设计。文献[4]针对机械产品的退化试验中，小样本数据下产品性能退化轨迹难以用准确的数学函数描述的问题，提出了基于盲数理论的性能退化数据可靠性分析方法。文献[5-7]针对发电系统、输电系统或配电网系统可靠性评估中的多种不确定性信息，提出了以盲数理论为基础的电力系统可靠性柔性评估模型，利用盲数表示各节点信息，有效地解决了原始参数不确定性对可靠性评估的影响问题。以上研究说明，盲数理论可有效地解决诸多领域中的可靠性评估中的不确定性问题。然而在机械工程再制造领域，裂纹扩展中的不确定因素导致结构载荷效应与抗力存在多种不确定性，这些不确定性引起的不同工况下裂纹缺陷结构可靠度问题有待展开进一步研究。

本文以萤火虫神经网络为基础，将不确定性因素盲数化的思想与裂纹强度因子和断裂韧性的干涉模型(KI-KIC模型，KI为应力强度因子，KIC为断裂韧性)相结合，从失效征候结构裂纹位置远场应力、裂纹扩展尺寸、结构材料断裂韧性等多种不确定性因素的角度研究承载结构的可靠度，实时预测不同工况下缺陷结构抵抗失效的能力，以及不同工况退出可行性工况域的先后顺序。

1 盲数理论

客观实际中，信息是由单式信息复合而成的混沌信息。在单式信息和混沌信息的应用中，从混沌信息中衍生出一种可处理具有最多4种不确定性的复杂信息，称之为盲信息，由此衍生出盲数理论[8-9]。

1.1 盲数定义

设g(I)为灰数集且xi∈g(I)，ai∈[0,1](i=1,2,…,n)，f(x)为定义在g(I)上的灰函数：

(1)

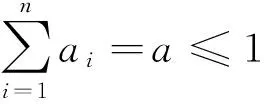
1.2 盲数运算

设盲数A、B分别为

(2)

i=1,2,…,n

则C=A⊗B(其中⊗可代表+，-,×,÷)，运算结果仍为盲数。盲数C可按以下步骤进行计算:

(1)构造A和B的可能值带边⊗矩阵(图1)及其可信度带边积矩阵(图2)。

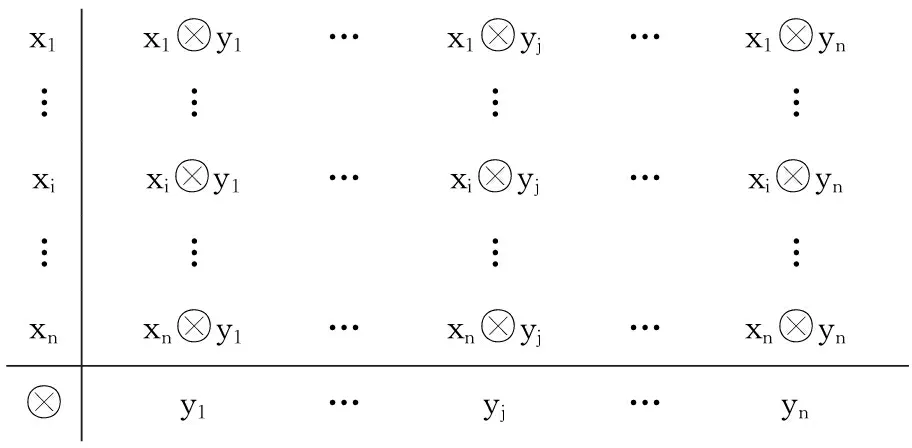
x1x1y1…x1yj…x1yn︙︙︙︙xixiy1…xiyj…xiyn︙︙︙︙xnxny1…xnyj…xnyny1…yj…yn

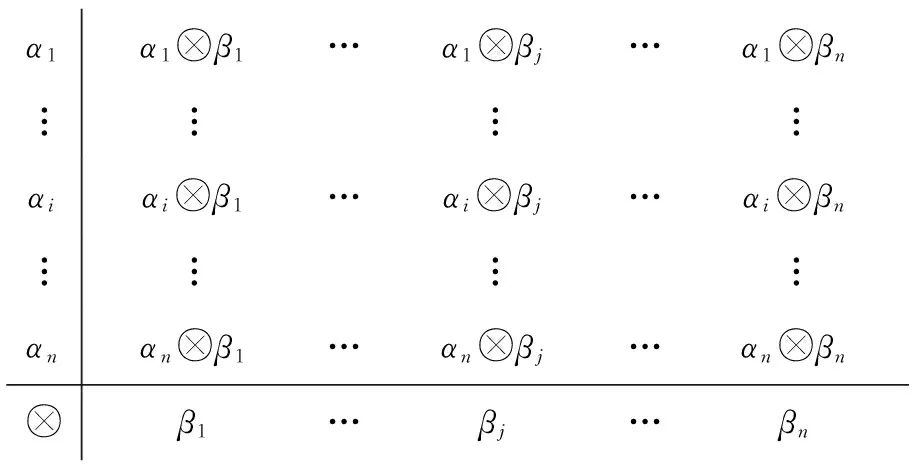
图1 A和B的可能值带边⊗矩阵

图2A和B的可信度带边积⊗矩阵

Fig.2 Confidence edge product⊗matrix ofAandB

(2)将A和B的可能值带边⊗矩阵中所有元素按照升序进行排列得到z1,z2,…,zk，相同的元素记为一个，若zi(i=1,2,…,k)对应的可能值带边⊗矩阵中有mi个不同位置，则将可信度带边积⊗矩阵中相对应的mi个位置上的元素记为γi，可得序列γ1,γ2,…,γk。

(3)

2 盲数失效征候结构可靠性

大型伸缩式臂架结构作为流动式起重机的主要承载构件，在长期的使用过程中，由于机械载荷、环境条件、腐蚀因素以及运输、装配过程中磕碰现象的影响，导致臂架结构中常常产生宏观尺度的裂纹。而宏观裂纹[10]的存在对于流动式起重机的安全使用是严重的隐患，裂纹的进一步扩展必将导致结构的断裂，轻则重物坠落，重则机毁人亡。裂纹作为臂架结构失效的一种征候，对其结构进行可靠性研究有着重要的意义。

在KI-KIC模型中，失效征候结构的可靠度表示裂纹应力强度因子不超过规定断裂韧性的概率，当裂纹应力强度因子超过结构的断裂韧性时，即判定结构失效。实际环境中，因受工作特点、工作环境、载荷作用性质、钢材性能、结构尺寸、检测周期、检测仪器等确定性因素和诸多不确定性因素的影响，存在某一特定失效征候的臂架结构，其自身结构载荷效应与抗力存在不确定性，从而导致强度因子与断裂韧性之间存在多种不确定性因素，其中包括随机不确定性、模糊不确定性以及设计、检测人员的认知不确定性等。以结构缺陷裂纹这一失效征候为例，针对多种不确定性因素，提出基于盲数理论的缺陷结构可靠性计算方法，构建盲数失效征候结构可靠度模型，如图3所示。

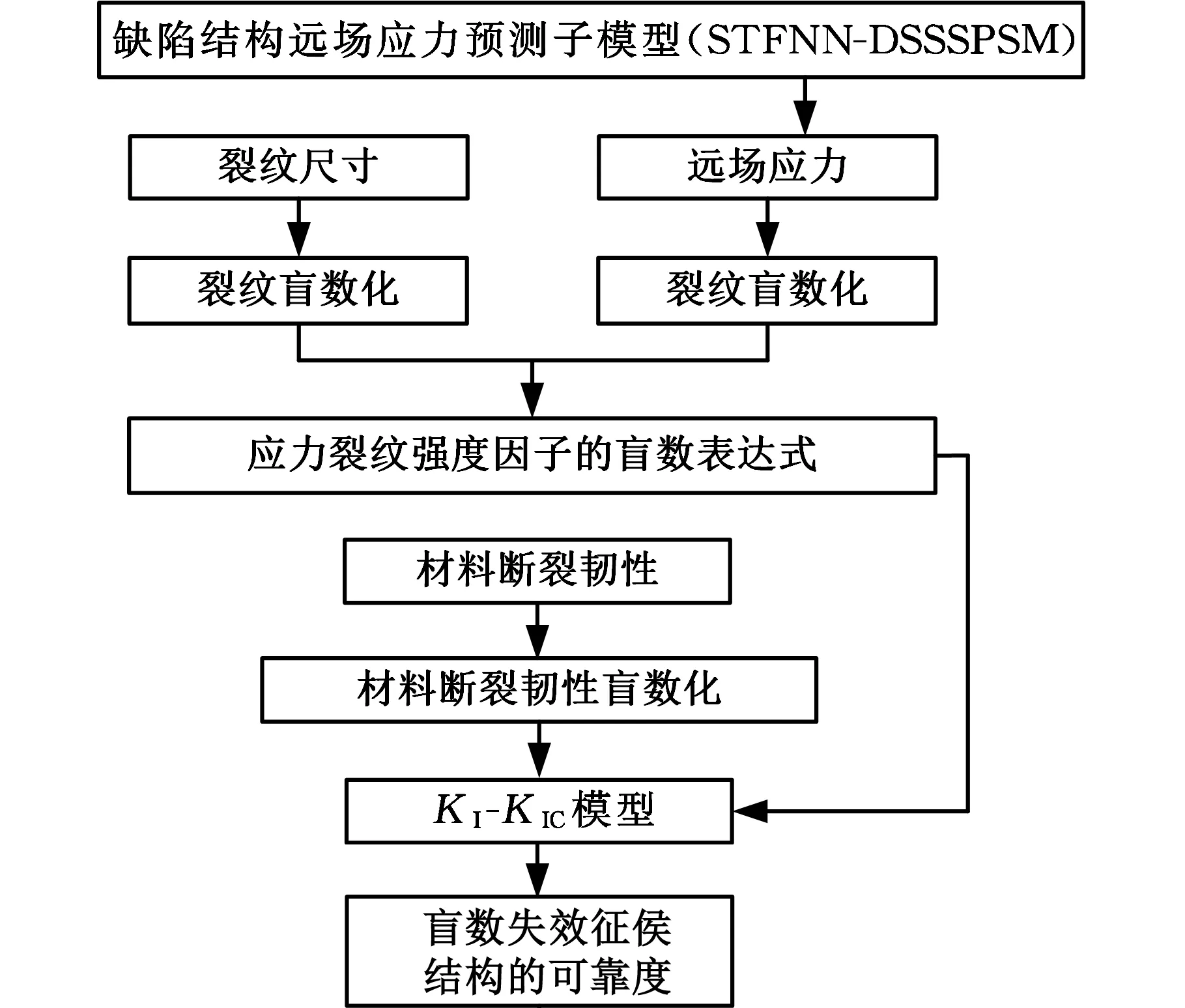
图3 盲数失效征候结构可靠度模型Fig.3 Reliability model of blind number failure symptom structure

设臂架结构裂纹尺寸为盲数f(x)，其表达式为

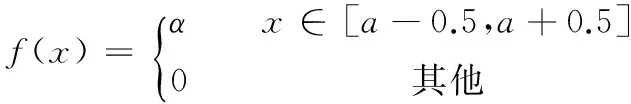
(4)

式中，a为结构裂纹尺寸，mm；α为f(x)在区间[a-0.5,a+0.5]的可信度，且α≤1。

根据试验、仿真、预测结果判断缺陷结构的远场应力分布，从而确定不同工况下远场应力的盲数表达式。假设远场应力满足标准正态分布，即σz～N(μ,σ2)，则远场应力的盲数表达式为

(5)

i=1,2,…,n-1

其中，μ为远场应力分布的期望，σ为远场应力的标准差，Φ为标准正态分布函数，且应满足:

(6)

应力裂纹强度因子计算公式为

(7)

将式(4)～式(6)代入式(7)，同时根据盲数运算规则(图1和图2)得到应力强度因子的盲数表达式:

(8)

j=1,2,…,k-1

以GH960号材料为例，设其断裂韧性为盲数f(KIC)，其表达式为

(9)

式中，β为f(x)在区间[67.5,72.5]的可信度，β≤1。

由可靠度的定义[11]，得到基于盲数理论的缺陷结构可靠度：

R=P(f(KIC)-f(KI)>0)

(10)

3 结构串行式萤火虫神经网络

萤火虫算法是由Yang[12]提出的一种新颖的群智能算法，具有良好的全局寻优特性，将该算法与神经网络相结合，可以有效地加快训练速度,减小训练误差[13]。

由于大型起重机械实物试验周期长、风险高、试验成本高昂、试验和测试手段不够全面、测试载荷与工况的选择过于单一，因而出厂前产品的原始性能参数以及使用后的退化性能参数(结构的实测强度、刚度及稳定性)难以获得。笔者以少量的试验结果为依据，结合有限元仿真技术，构建STFNN-DSSSPSM、STFNN-DSRPSM，实现任意工况下的远场应力以及不同缺陷程度下结构的可靠度预测，以此为基础，评估结构抵抗失效的能力以及不同工况退出可行性工况域的先后顺序。

3.1 萤火虫神经网络的编码方式

根据在役起重机臂架结构特征参数(图4)，包括缺陷结构原始特征和缺陷特征，确定神经网络实际输入xi(i=1,2,…,n)，其中，x1,x2,…,xn-1由缺陷结构原始特征确定，xn由缺陷特征确定(进行缺陷结构远场应力测试时，xn为0)、实际输出yj(j=1,2,…,l)(当xn为0时，实际输出为缺陷结构的远场应力；当xn不为0时，输出缺陷结构的可靠度)、目标输出tk(k=1,2,…,l)、输出误差为ek，同时根据经验公式[14]确定隐含层的节点数q，从而确定神经网络的拓扑结构为n-q-l型,如图5所示。以n-q-l型网络结构为基础，确定萤火虫的编码方式，若n=2,q=3,l=1,则编码结果如图6所示。

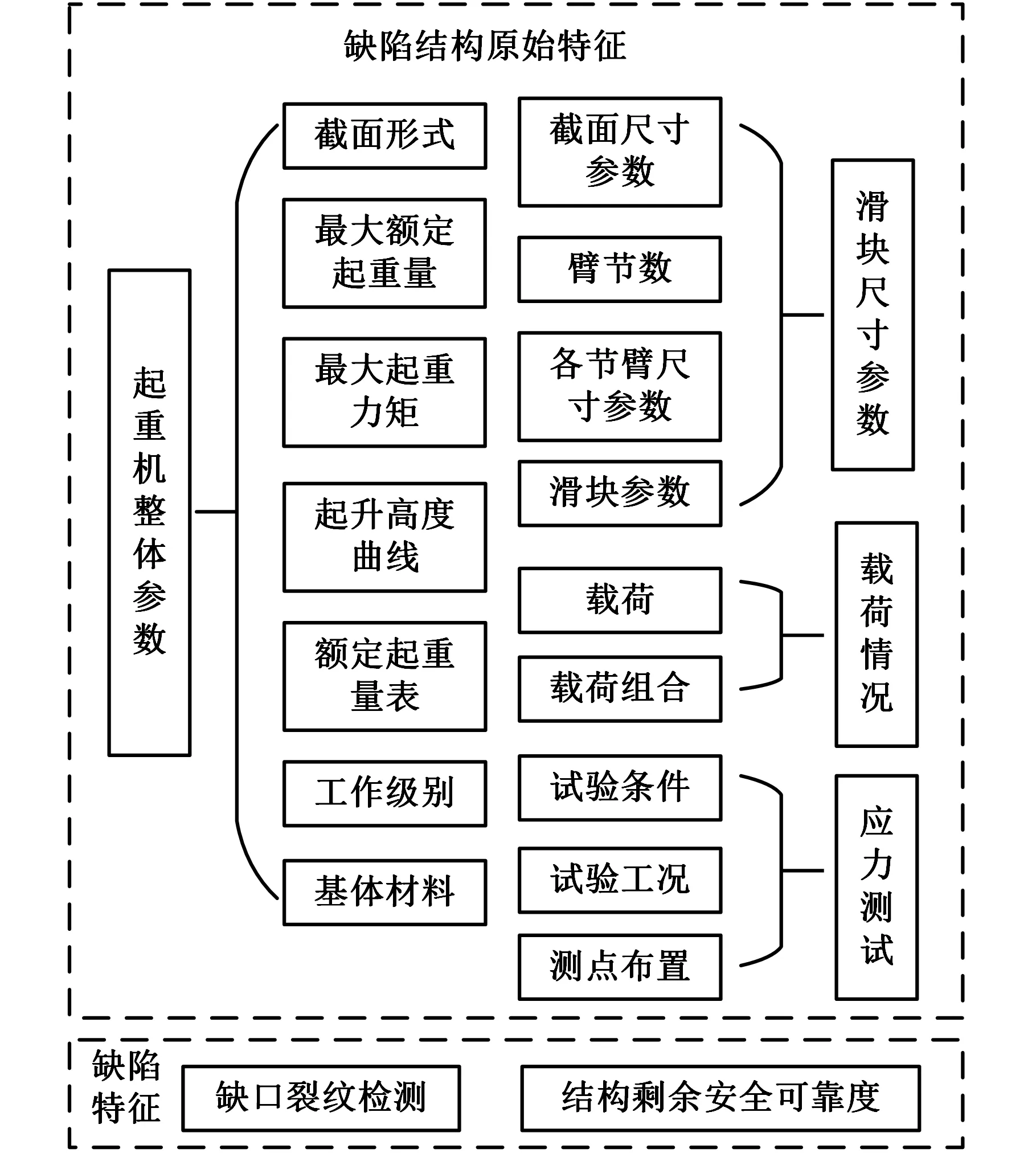
图4 在役起重机臂架结构特征参数Fig.4 Characteristic parameters of jib structure of crane in service

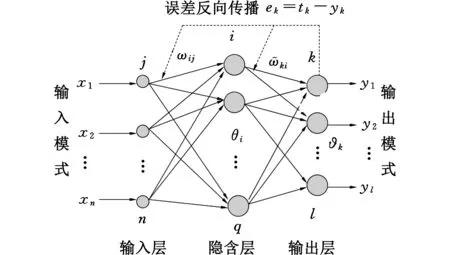
图5 神经网络拓扑结构Fig.5 Neural network topology

图6 2-3-1型网格编码方式Fig.6 2-3-1 trellis coding

3.2 萤火虫神经网络的适应度函数

萤火虫的适应度与BP神经网络训练的精度有关，且训练精度越高，适应度越大，因此，可通过神经网络的二次型误差函数来确定萤火虫的适应度，具体按下式进行计算:

(11)

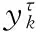
隐含层第i个节点(i=1,2,…,q)的输入-输出为

(12)

式中，zi、oi分别为隐含层第i个节点输入和输出；ωij为输入层第j个点到隐含层第i个点的连接权值；θi为隐含层第i个点的阈值。

输出层第k个节点(k=1,2,…,l)的输入-输出为

(13)

式中，pk、yk分别为输出层第k个节点的输入和输出；ϖki为隐含层第i个点到输出层第k个点的连接权值；ϑk为输出层第k个点的阈值。

3.3 结构的串行式萤火虫神经网络预测

结构失效征候的萤火虫神经网络预测过程包括两部分:缺陷结构远程应力预测和缺陷结构安全可靠性预测，预测模型如图7所示，其中路径①为STFNN-DSSSPSM，路径②为STFNN-DSRPSM。具体过程如下。

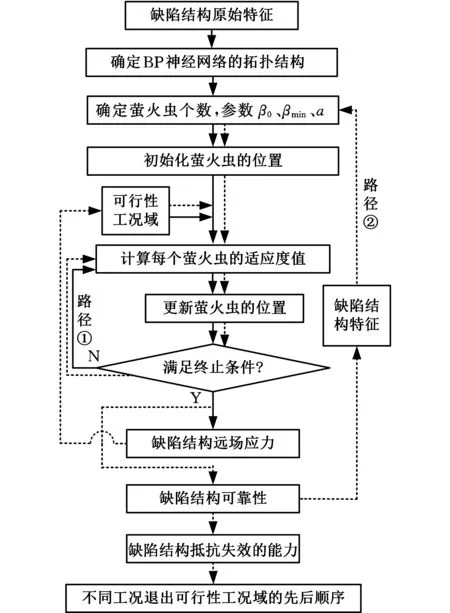
图7 失效征候结构的STFNNPMFig.7 STFNNPM of failure symptom structure

(1)以缺陷结构的原始特征为基础，确定BP神经网络的拓扑结构。

(2)确定萤火虫种群数量m，并设置参数β0、βmin、a、最大迭代次数tmax及误差精度ε。

(3)在搜索空间内初始化m个随机的萤火虫的位置：X={X1,X2,…,Xm},第i个萤火虫的位置Xi=(xi1,xi2,…,xin)T(其中，xin=0)将其作为优化问题的一个潜在解。

(4)输入缺陷结构可行性工况域的原始参数样本，根据式(10)～式(12)计算每个萤火虫的适应度，即个体的亮度。

(5)若第j个萤火虫的亮度小于第i个萤火虫的亮度(i,j=1,2,…,m且i≠j)，则Xi保持不变，Xj向Xi移动，可按下式进行计算:

b(ζ-0.5)

(14)

其中，k为迭代次数；β0为吸引力系数，通常取1；βmin为吸引力下限，βmin∈[0,1]；γ为光吸收系数，γ=0.5/L2(L为变量尺度)；b为步长因子；ζ∈[0,1]为随机系数；rij为任意两个萤火虫之间的欧氏距离，可按下式进行计算：

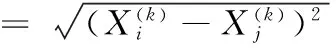
(15)

(6)第i个萤火虫随机移动:

(7)若达到最大迭代次数或满足误差精度时，迭代终止，转步骤(8)，否则转步骤(4)。

(8)当xin为0时，用训练好的网格预测缺陷结构的远场应力，同时以结构失效征候的盲数可靠性为理论基础，计算缺陷结构的安全可靠性；当xin不为0时，用训练好的网格预测缺陷结构的可靠度。

(9)将缺陷结构可靠度作为补充部分对输入样本进行更新，同时结合缺陷结构特征，更新萤火虫的位置，转步骤(2)，此时xin不为0。

(10)可行性工况域内，以缺陷结构的可靠度为依据，分析不同工况下，缺陷程度对结构抵抗失效能力的影响，以及不同工况退出可行性工况域的先后顺序。

4 工程实例

以某企业生产的在役QY130t汽车起重机为例，针对缺口裂纹这一特定失效征候，在可行工况域内，预测其主臂架结构缺陷结构的可靠度，分析不同缺口裂纹程度(裂纹扩展尺寸)对结构抵抗失效能力的影响以及不同工况退出可行性工况域的先后顺序。该起重机的整机参数:截面形式为U形，最大额定总起重质量为130 t，最大起重力矩为5056 kN·m，起升高度曲线、额定起重量表、结构尺寸可参考文献[15]，工作级别为A4，基体材料为GH960，缺口裂纹的位置如图8所示，试验工况可分为典型工况和普通工况。典型工况包括：臂架全伸下工作幅度最小(工况1)；臂架全伸下工作幅度最大(工况2)；臂架全缩下工作幅度最小(工况4)；臂架全缩下工作幅度最大(工况6)。除典型工况外，剩余的均为普通工况。对各工况的描述指标包括工作时臂架总长度、工作幅度，除基本臂外各臂节的伸出量、试验时的实际起升载荷，具体取值及对应的远场应力试验结果如图9所示，具体取值见表1(试验结果来源于企业)。

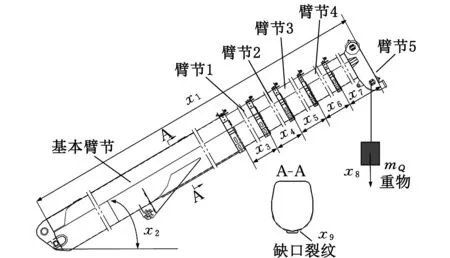
图8 主臂架基本臂节上的缺口裂纹Fig.8 Notch crack on basic arm sections of main jib

4.1 结构可行性工况下的远场应力预测

通过对在役QY130t汽车起重机臂架结构特征参数的研究，确定其主臂架基本臂节(图8)上缺口裂纹导致臂架结构失效的主要因素，包括主臂长度、幅度、各节臂的伸出长度(除基础臂外有5节伸缩臂)、载荷、缺口裂纹长度，共9个特征，即x1,x2,…,x9，其中，x9为扩展特征。由于缺口裂纹长度对结构远场应力的影响甚微[15]，故进行远场应力预测时，令扩展特征x9=0。将特征向量x=(x1，x2，…，x9)归一化[14]后作为萤火虫神经网络的输入特征，将缺口裂纹处远场应力的最大值t1与最小值t2作为目标输出向量T的元素，即T=(t1,t2)，从而确定萤火虫神经网络的拓扑结构为9-19-2型。用表1中的8组数据作为数据样本，前6组用于训练学习样本，后2组用于验证训练好的网格的有效性。

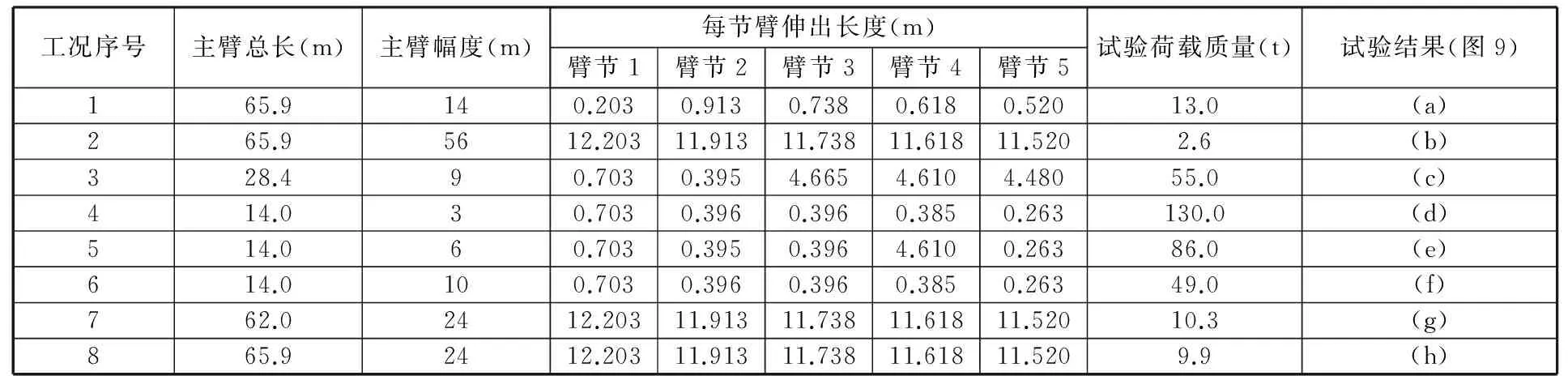
表1 缺口裂纹1处远场应力的试验结果

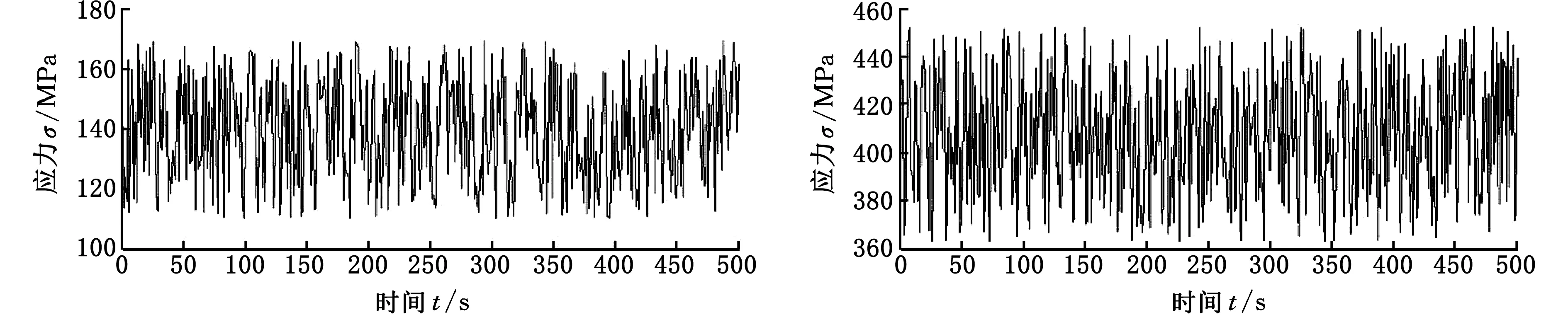
(a)工况1 (b)工况2

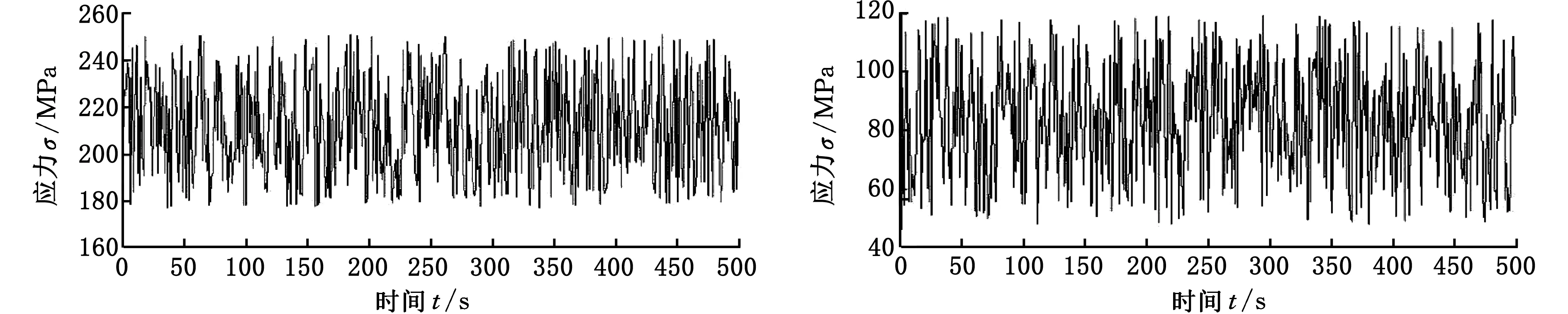
(c)工况3 (d)工况4

(e)工况5 (f)工况6

在MATLAB 2010b环境下运行萤火虫神经网络算法，进行裂纹缺陷结构远场应力预测，算法的参数如下:种群数量m=20，β0=1，βmin=0.15，a=0.1,γ=0.9，最大迭代次数tmax=5000，误差精度ε=0.005，训练结果如图10所示，实际误差为0.004 194 6，迭代时间T=1.258 s。利用表1中后3组(工况6、7、8)数据，对训练好的STFNN-DSSSPSM进行有效性验证。预测值与实际值的比较结果见表2。由表2可以看出，预测结果与实际值非常接近，表明训练后的STFNN-DSSSPSM达到预测效果。

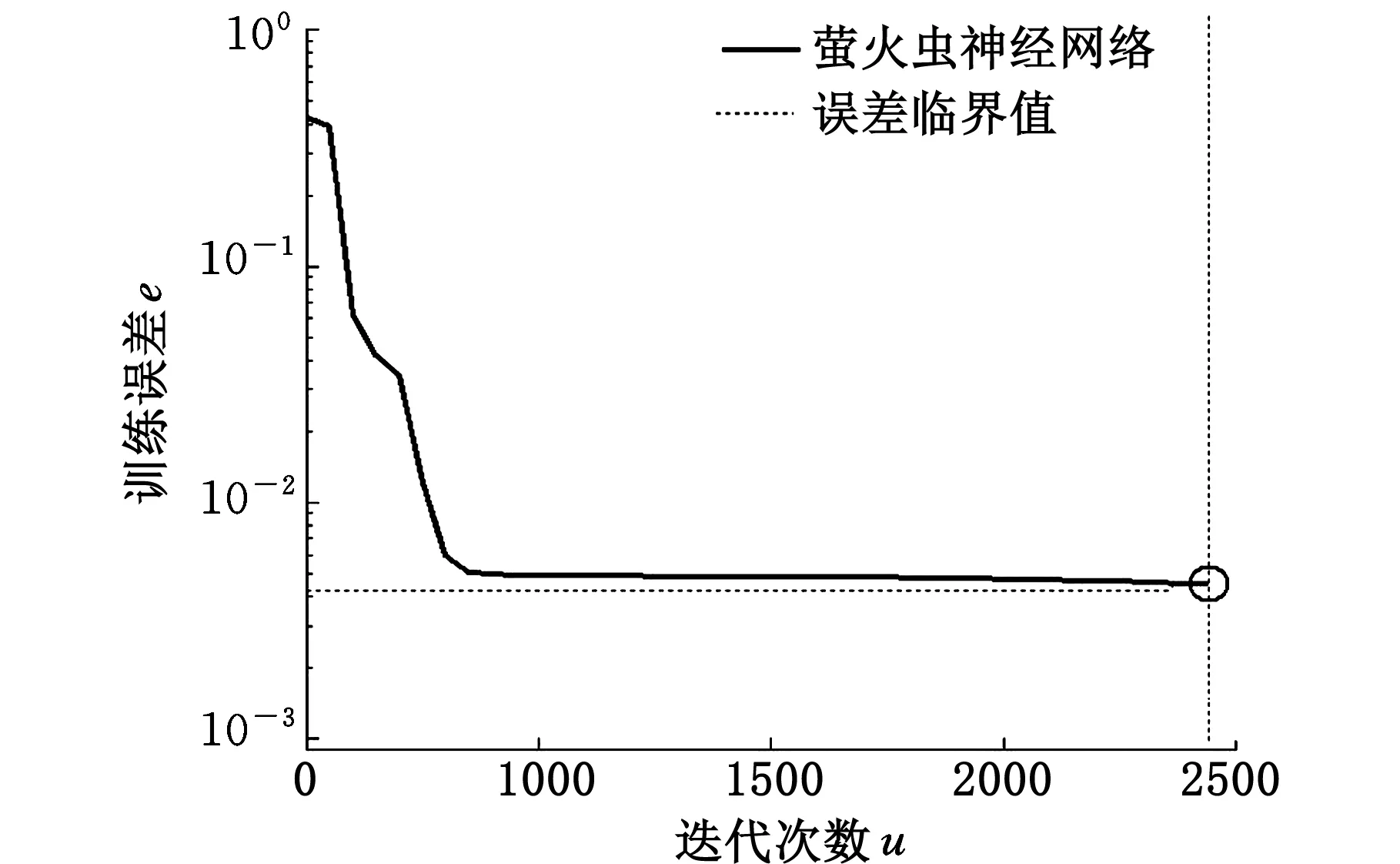
图10 远场应力的萤火虫神经网络训练曲线Fig.10 Neural network training curve of far field stress

基于STFNN-DSSSPSM，通过输入流动式起重机臂架结构的可行性工况数据(由图11所示起升高度曲线和额定起重量表获得)，可以实时预测结构在缺口裂纹处的远场应力，预测结果见表3。

将以上预测结果与有限元仿真结果进行对比，结果如图12所示。由图12可以看出，预测结果与有限元仿真结果非常接近。由此，进一步证明了STFNN-DSSSPSM的有效性与科学性。

图11 起升高度曲线Fig. 1 Lifting height curve

工况序号远场应力预测值(MPa)远场应力实际值(图9f～图9h)(MPa)相对误差(%)最大值最小值最大值最小值最大值最小值6121.70484.298120.53184.7900.97320.58037318.294290.955317.252299.3110.32842.79178291.997277.985292.354273.9830.12211.4607

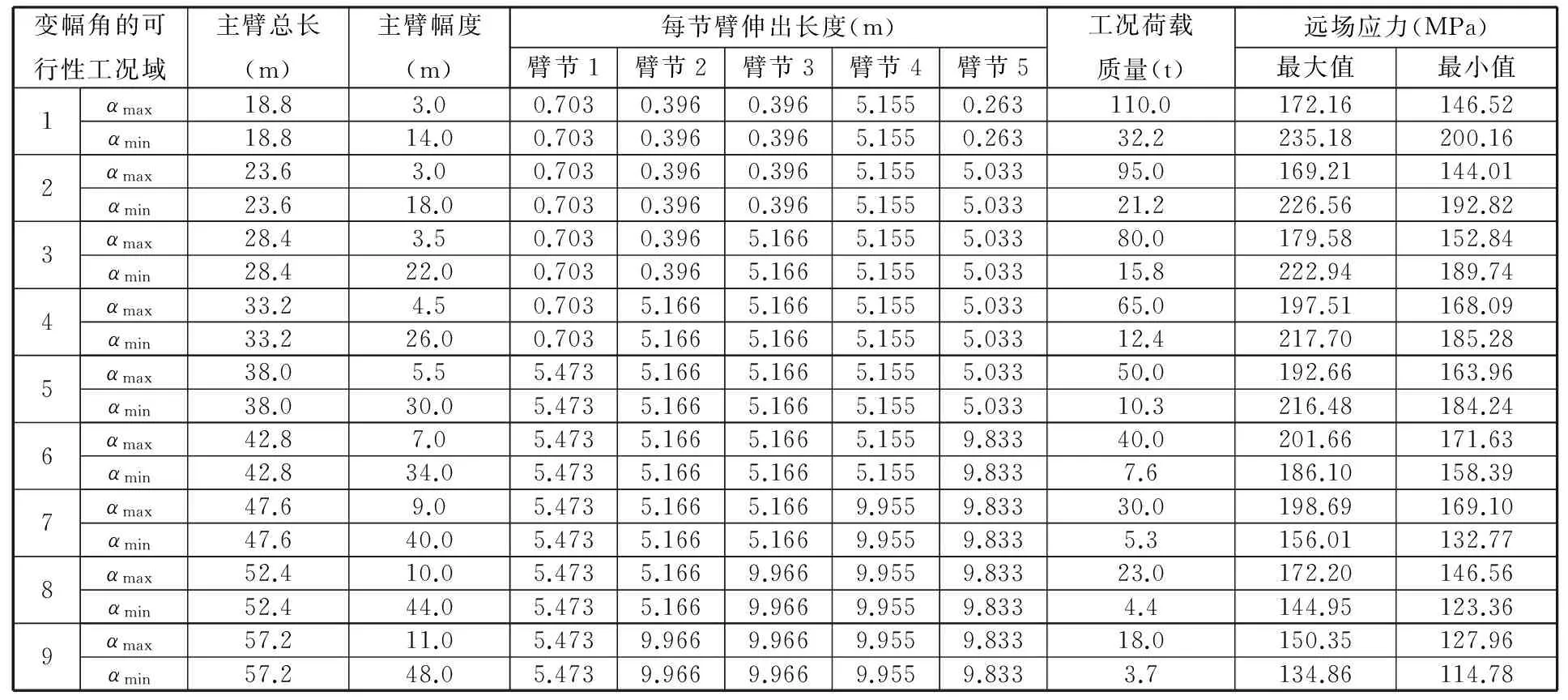
表3 可行性工况远场应力预测结果

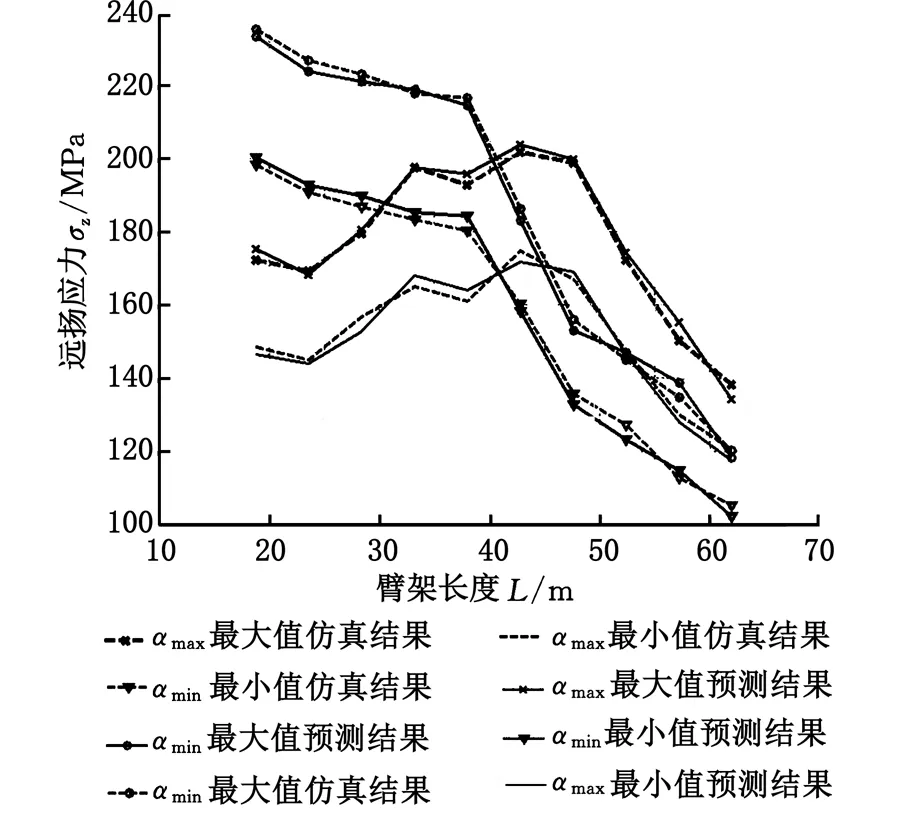
图12 远场应力的预测与有限元仿真结果Fig.12 Prediction of far field stress and finite element simulation results

4.2 盲数失效征候臂架结构可靠度

由试验仿真数据知，裂纹位置远场应力σz服从正态分布，因此，以盲数理论为基础，根据裂纹位置远场应力σz、裂纹长度a以及材料断裂韧性KIC的分布情况，确定不同工况下远场应力σz、裂纹长度a、国产GH960断裂韧性KIC的盲数表达式，以变幅角最大的前三种工况为例，给出具体的盲数表达式(其余工况与此类似，不再赘述)。

工况1下σz的盲数表达式为

(16)

工况2下σz的盲数表达式为

(17)

工况3下σz的盲数表达式为

(18)

裂纹尺寸的盲数表达式为

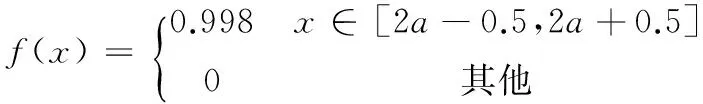
(19)

断裂韧性的盲数表达式为

(20)

根据盲数四则运算法则(图1、图2)，将可行性工况的远场应力以及裂纹长度的盲数表达式代入式(7)，得到臂架结构裂纹强度因子的盲数表达式，再将强度因子的盲数表达式与断裂韧性的盲数表达式代入式(10)，从而得到裂纹缺陷下臂架结构的可靠度，具体结果如图13～图15所示。

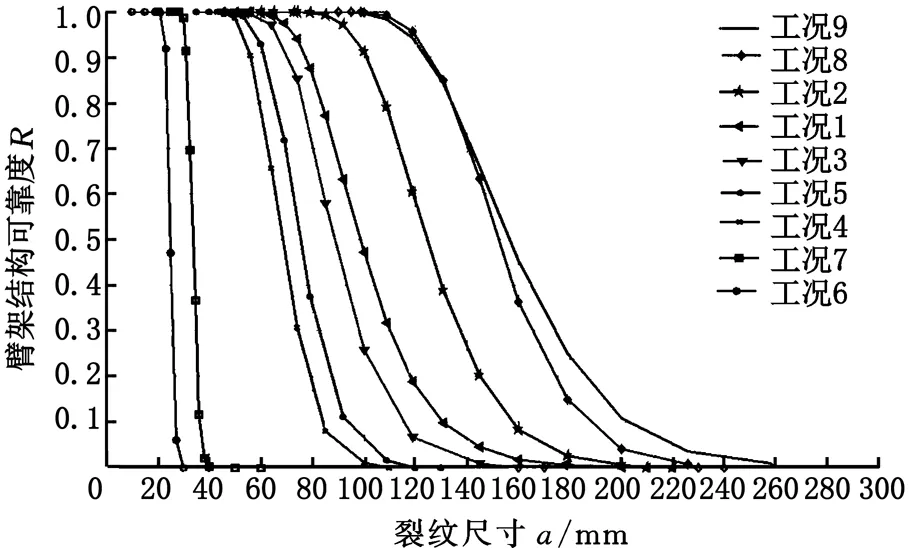
图13 最大变幅角的臂架结构可靠度Fig.13 Jib structure reliability under maximum amplitude angle

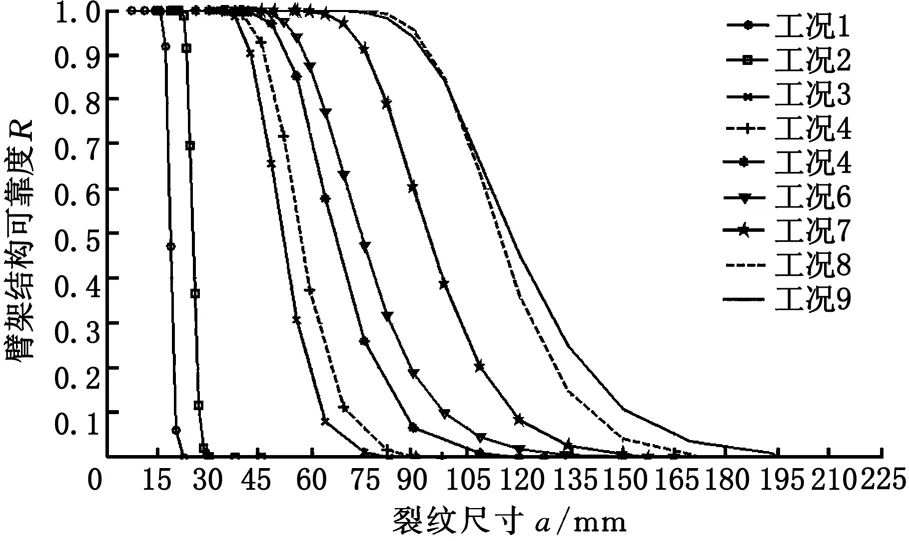
图14 最小变幅角的臂架结构可靠度Fig.14 Jib structure reliability under minimum amplitude angle

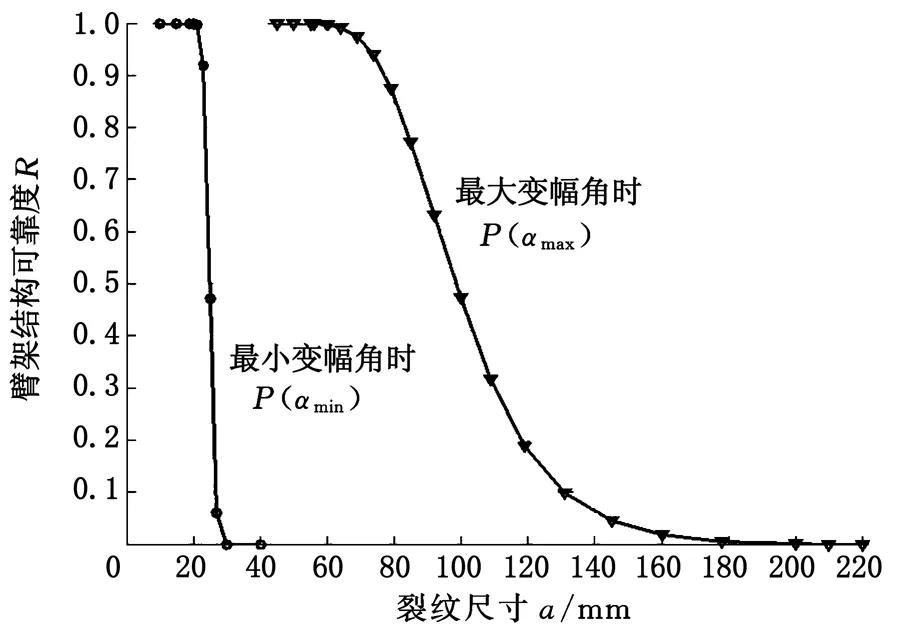
图15 极限变幅角的臂架结构可靠度曲线(工况1)Fig.15 Reliable curve of jib structure under limit amplitude angle(condition one)

由图13可以看出，臂架处于最大变幅角时，工况6、工况7受裂纹扩展影响最严重，即较小的裂纹尺寸扩展量导致臂架结构的可靠度大幅下降，说明在这两种工况下，臂架结构抵抗裂纹的扩展能力弱；随着裂纹尺寸的增大，各工况退出可行性工况域的先后顺序为:工况6-7-4-5-3-1-2-8-9。

由图14可以看出，可行性工况域内，臂架处于最小变幅角时，随着臂架长度的增加，额定起重质量减小，其自身抵抗裂纹的扩展能力逐渐变强；随着裂纹尺寸的增大，各工况退出可行工况域的先后顺序为:工况1-2-3-4-5-6-7-8-9。

由图15可以看出，以工况1为例，臂架长度保持不变，变幅角增大时，额定起重质量增大，臂架结构抵抗裂纹的扩展能力增强，且对于任意的变幅角α∈[αmin,αmax]时，总有一条可靠度曲线P(α)存在于由P(αmin)和P(αmax)所构成的闭包区域内，且变幅角越小，越先退出可行工况1。

4.3 失效征候臂架结构可靠度预测

以表3为基础样本，利用极限位置臂架结构可靠度曲线(图13和图14)对基础样本进行扩展，得到失效征候臂架结构可靠度预测样本，以工况1为例，预测样本结果见表4，其余工况与其类似。同时将某一特定裂纹尺寸作为扩展特征x9(萤火虫神经网络输入特征向量x中的元素)的输入，臂架结构可靠度作为目标输出。

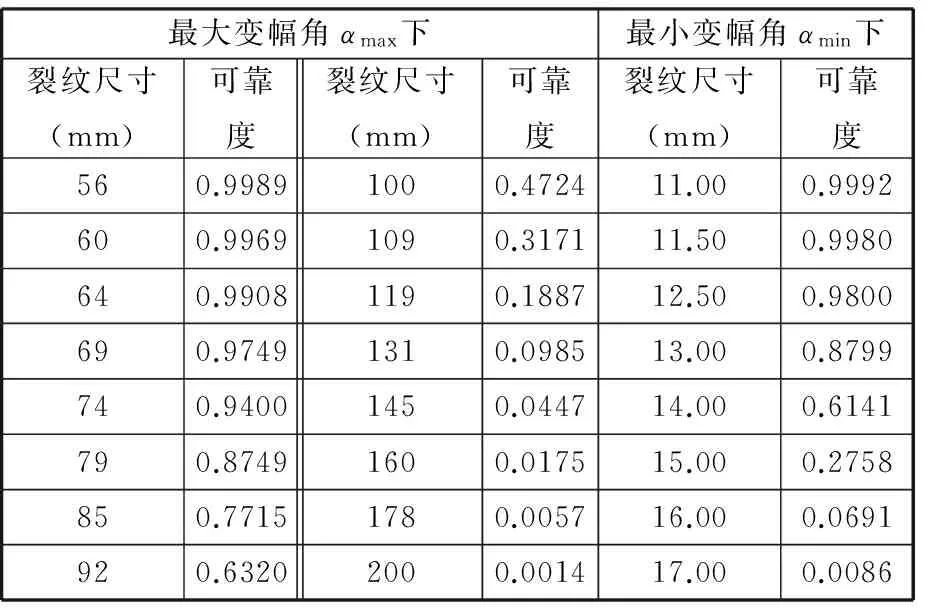
表4 工况1的失效征候臂架结构可靠性预测样本

在9种可行性工况的失效征候臂架结构可靠度预测样本数据中，前7种工况的样本数据用于训练学习样本，后2种用于验证STFNN-DSRPSM的有效性。

在进行预测时，除误差精度ε=1×10-5外，其余参数与远场应力预测算法的参数相同，训练结果如图16所示，实际误差为9.4234×10-7。用工况8、工况9的变幅角最大时的数据样本对训练好的STFNN-DSRPSM进行验证，验证结果如图17所示。

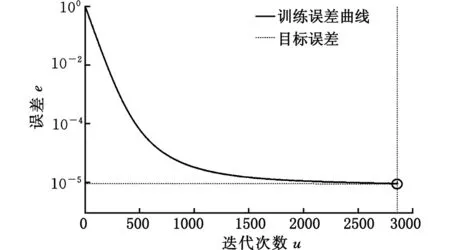
图16 结构可靠度的萤火虫神经网络训练曲线Fig.16 Neural network training curve of structural reliability

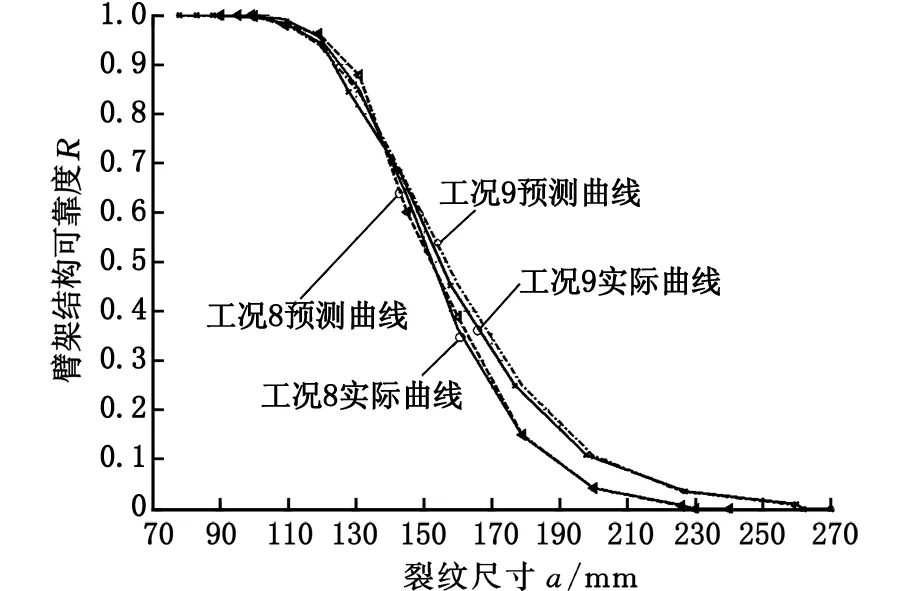
图17 预测曲线与实际曲线Fig.17 Prediction curve and actual curve

由图17可以看出，预测曲线非常接近实际曲线。因此，训练后的STFNN-DSRPSM已达到预期效果。以上述模型为基础，通过输入臂架起升工况，可实时预测不同工况、不同裂纹扩展尺寸下缺陷结构的可靠度，再以此为基础，可以得到缺陷臂架结构抵抗裂纹扩展的能力、随裂纹的扩展以及不同工况退出可行性工况域的先后顺序。

5 结论

(1)针对臂架结构裂纹缺陷的特定失效征候，将盲数理论引入裂纹尺寸、裂纹缺陷处远场应力、结构材料断裂韧性中，构建了盲数失效征候结构可靠度模型(BNFSSRM)，提出了盲数失效征候结构可靠度计算方法。

(2)针对工程机械在役产品的原始性能参数以及使用后的退化性能参数难以获得的问题，构建串行式萤火虫神经网络预测模型(STFNN-DSSSPSM与STFNN-DSRPSM串联)，提出了在役产品的串行式萤火虫神经网络预测方法，以少量的试验结果为依据，结合有限元仿真技术，通过引入萤火虫神经网络来预测缺陷结构的远场应力以及不同缺陷程度下结构的可靠度。

(3)以在役QY130t流动式起重机臂架结构为例，基于盲数失效征候结构可靠度计算方法，通过预测可行性工况下裂纹缺陷结构的远场应力，得到不同工况下裂纹扩展尺寸对臂架结构可靠度的影响。

(4)以STFNN-DSRPSM为基础，通过输入臂架起升工况，可实时预测不同工况、不同裂纹扩展尺寸下缺陷结构的可靠度，从而确定缺陷臂架结构抵抗裂纹扩展的能力，以及随着裂纹的扩展，不同工况退出可行性工况域的先后顺序。

[1] 郭朋彦,石博强,肖成勇,等.基于盲数理论的机械结构复杂时变可靠性计算方法[J].农业机械学报, 2010, 41(9):210-213. GUO Pengyan, SHI Boqiang, XIAO Chengyong, et al. Computing-algorithm for Time-dependent Reliability of Mechanical Structure Based on Blind Number[J].Transactions of the Chinese Society for Agricultural Machinery,2010, 41(9):210-213.

[2] 赵德祥, 石博强.基于盲数理论的车架结构可靠性计算[J].矿山机械, 2007(11):60-62. ZHAO Dexiang, SHI Boqiang.Reliability Calculation of Frame Structure Based on Blind Number Theory[J].Mining & Processing Equipment, 2007(11):60-62.

[3] 李海鹏,石博强, 张文明,等.基于盲数理论的机械强度可靠性优化设计[J].机械强度,2007, 29(3):425-428. LI Haipeng, SHI Boqiang, ZHANG Wenming, et al. Reliability-based on Optimization Design of Mechanical Strength Based on Blind Number Theory[J]. Journal of Mechanical Strength, 2007, 29(3):425-428.

[4] 杨恒, 徐格宁, 韩子渊. 基于盲数理论的性能退化数据可靠性分析[J].机械强度,2013, 35(6):777-782. YANG Heng,XU Gening, HAN Ziyuan. Reliability Analysis on the Data of Performance Degradation Based on the Blind Number Theory[J]. Journal of Mechanical Strength, 2013, 35(6):777-782.

[5] 王磊，张明文，王秋莎. 基于盲数理论的输电系统可靠性评估[J]. 电力科学与工程，2010，26(8):4-9. WANG Lei,ZHANG Mingwen,WANG Qiusha. Reliability Evaluation of Transmission System Based on Blind Number Theory[J]. Electric Power Science and Engineering, 2010，26(8):4-9.

[6] 陈剑勇，蔡红梅，苏浩益.盲数理论在发电系统可靠性评估中的应用[J]. 电力系统保护与控制，2012，40(13):74-77. CHEN Jianyong, CAI Hongmei, SU Haoyi. Application of Blind Number Theory in Power Generation System Reliability Evaluation[J]. Power System Protection and Control, 2012，40(13):74-77.

[7] 赵书强，王海巍. 基于盲数的配电系统可靠性评估[J]. 电力系统保护与控制，2011，39(16):8-12. ZHAO Shuqiang, WANG Haiwei. Power Distribution System Reliability Evaluation Based on Blind Number[J]. Power System Protection and Control, 2011，39(16):8-12.

[8] 刘开第，吴和琴，庞彦军，等.盲数的概念、运算与性质[J]. 运筹与管理，1998,7(3):14-17. LIU Kaidi, WU Heqin, PANG Yanjun,et al. Concept Operations and Properties of Blind Number[J].Operations Research and Management Science, 1998, 7(3):14-17.

[9] 孟衡，李建林. 基于盲数理论的关键块体稳定性分析研究[J]. 水电能源科学, 2009, 2(3):117-119. MENG Heng, LI Jianlin. Research on Key Block Stability Based on Blind Number Theory[J]. Water and Electricity Energy Science, 2009, 2(3):117-119.

[10] 赵章焰.机械承载结构裂纹诊断、控制与维修方法的研究及应用[D].武汉:武汉理工大学, 2001. ZHAO Zhangyan.Study on Mehtod of Notch-crack Diagnosing,Controlling and Maintaining and Its Application for Mechanical Loading-carrying Structure[D].Wuhan:Wuhan University of Technology, 2001.

[11] 刘惟信. 机械可靠性设计[M].北京:清华大学出版社，1996. LIU Weixin. Mechanical Reliability Design[M]. Beijing: Tsinghua University Press, 1996.

[12] YANG X S.Nature-inspired Metaheuristic Algorithms[M].Luniver Press,2008.

[13] 李国勇，杨丽娟.神经·模糊·预测控制及其MATLAB实现[M].北京:电子工业出版社,2013. LI Guoyong, YANG Lijuan. Nerve, Fuzzy, Predictive Control and MATLAB Implementation [M].Beijing: Electronics Industry Press, 2013.

[14] 翁胜龙. 基于萤火虫算法的聚类分析与神经网络诊断方法[D].广州：华南理工大学，2014. WENG Shenglong. A Clustering Method and A Neural Network Based on Firefly Algorithm in Diagnostic Analysis[D].Guangzhou：South China University of Technology, 2014.

[15] 韩晓君.在役实腹式臂架可视裂纹失效仿真及寿命评估[D]. 太原：太原科技大学, 2015. HAN Xiaojun. Solid-web Boom in Service Visual Notch-crack Failure Simulation and Life Assessment[D].Taiyuan:Taiyuan University of Science and Technology,2015.

(编辑 陈 勇)

Firefly Neural Network Failure Symptom Structure Reliability Prediction Based on Blind Number Theory

DONG Qing XU Gening

School of Machinery and Electronics Engineering,Taiyuan University of Science and Technology, Taiyuan,030024

Under any feasibility conditions, the reliability of large arm structure with failure symptoms was difficult to be determined due to various uncertain factors of load effects and resistances in notch-crack propagation. The firefly neural network prediction method of the reliability of structure with failure symptom was presented based on the blind number theory by building a blind number failure symptom structure reliability model (BNFSSRM), serial type firefly neural network prediction model consisting of far field stress prediction sub-model (STFNN-FFSPS) and reliability prediction sub-model (STFNN-RPS) of damaged structure. On the basis of the stress-strength interference model, the firefly neural network being as a forecasting method, the idea converting the uncertainty problems to blind numbers was introduced into the interference model of intensity factors of notch-crack and fracture toughness according to the rule of notch-crack instability propagation, and the reliability of notch-crack damaged structure was obtained by the experiments and finite element simulation combined with STFNN-FFSPS under typical working conditions. The reliability being taken as the target output and the notch-crack size being as the input data of expanded samples, the real-time prediction of reliability of damaged structure may be achieved by BNFSSRM and STFNN-RPS, thus realizing the evaluation of the capacity of the structure resistant to failure and determining the orders of different conditions out of the feasible condition regions. QY130 remanufacturing arm structure was taken as an example and the effectiveness of the proposed method were verified.

blind number theory; failure symptom; notch-crack damaged; firefly neural network

2016-06-20

国家高技术研究发展计划(863计划)资助项目(2013AA040203)；“十二五”国家科技支撑计划资助项目(2011BAK06B05-05)

TB114.3

10.3969/j.issn.1004-132X.2017.15.006

董 青，女，1989年生。太原科技大学机械工程学院博士研究生。研究方向为安全评估、绿色再制造、寿命预测。E-mail:dongqing1989@outlook.com。徐格宁，男，1955年生。太原科技大学机械工程学院教授、博士研究生导师。