脉动血流发生器非圆齿轮-曲柄滑块式驱动机构设计与分析

陶德华 王 英 陈建能 荣权升 周 贤 束学道

1.宁波大学机械工程与力学学院，宁波，3152112.浙江理工大学机械与自动控制学院，杭州，310018

脉动血流发生器非圆齿轮-曲柄滑块式驱动机构设计与分析

陶德华1王 英1陈建能2荣权升1周 贤1束学道1

1.宁波大学机械工程与力学学院，宁波，3152112.浙江理工大学机械与自动控制学院，杭州，310018

为使脉动血流发生器产生稳定的脉动性血流，提出了一种新型非圆齿轮-曲柄滑块式驱动机构，运用非圆齿轮副和曲柄滑块机构的组合传动来实现血流的脉动。在满足人体血流脉动前提下，为使设计的机构运行平稳，采用2段三次Hermite插值多项式来对该机构输出构件的加速度曲线进行拟合，再由加速度曲线方程及其边界条件推导出速度、位移和跃度曲线方程，运用拟合得到的输出构件运动学曲线方程推导出非圆齿轮副节曲线反求模型。根据实例求解分析得到的机构参数进行三维建模和虚拟样机实验，对比虚拟仿真实验和理论分析结果，发现所设计机构能够按照预期规律实现脉动血流，且该机构具有良好的运动学特性，同时验证了所构建的运动学曲线方程及所建立的运动学分析模型的正确性。

脉动血流发生器；非圆齿轮；曲柄滑块机构；Hermite插值；运动学特性

0 引言

人体内血液在心脏搏动的作用下呈现脉动性流动[1-2]。在进行心脏手术[3]的过程中，为保持人体血液实现正常流动，保障人体正常新陈代谢，人体血液通过体外循环[4]过程后重新流入人体。血液体外循环的设备主要是人工心肺机[5]，其中动脉泵[6]是人工心肺机的核心部分，其主要作用是代替患者的心脏维持患者正常的血液循环。目前临床上常用的有滚压泵和离心泵[7]，经过此类泵体的血液流入人体为一稳定流，非人体正常活动时的脉动流。TAKEDA[8]研究发现，若是人体血液流动为一稳定流，会造成人体内毛细血管破裂和人体内部微循环形成分流等危害。PARSONS等[9]研究表明，人体血液流动呈脉动性变化时，人体内的组织液流动速度和体内淋巴形成速度都普遍高于人体血液为稳定流时，因此为使手术时血液循环过程产生脉动性血流，需添加一辅助装置——脉动血流发生器。目前市场上常采用气动和电动的驱动方式[10]，推动活塞按设计的运动规律往复直线运动，实现血液的加速和减速，产生脉动血流，为了提供稳定的脉动血液，其气电控制系统需要具备较高的稳定性，因此此类装置通常结构复杂，控制难度较大，造价较高[11]。另外，这两种驱动方式控制脉动血流发生器工作时会产生较大噪声[12]，不适用于需要相对安静环境的手术室。

针对上述问题，本文根据人体血流脉动法则，提出一种新型脉动血流发生器驱动机构，该机构通过非圆齿轮副和曲柄滑块机构的组合传动，实现稳定可靠的脉动血流。为了得到能够实现脉动血流理想运动规律的机构参数，并使设计的机构运行平稳，本文首先采用Hermite插值多项式拟合出该驱动机构输出构件需要满足的运动曲线，然后在建立该机构运动学分析模型的基础上，推导出非圆齿轮副节曲线反求模型，并基于MATLAB编写了该机构辅助设计与分析软件，最后通过实例分析验证所建立的分析模型的正确性及该机构良好的传动特性。

1 脉动血流发生器非圆齿轮-曲柄滑块式驱动机构工作原理

人体脉动血流产生原理如图1所示，图1a表示此时血管处于舒张阶段，血管内腔容积增大，此时血量增加使得血流流速减缓；图1b表示此时血管受到外部挤压，受挤压血管处内腔容积变小，血液流速增大。这样周期性的血管舒张和收缩使得人体血流流速产生脉动性变化[1]，从而达到产生脉动血流的目的。基于此原理，脉动血流发生器通过控制活塞的直线运动来实现体外循环血液流速的变化。

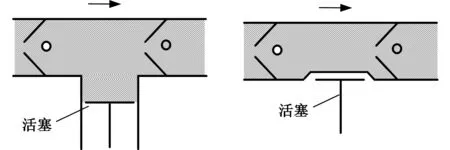
(a)血管舒张状态(b)血管收缩状态图1 血流发生脉动性变化原理图Fig.1 Schematic of pulsatile changes of blood flow

曲柄滑块机构[13]是用曲柄和滑块来实现转动和移动相互转换的机构，结构简单，加工制造方便，且易得到较高的制造精度。图1中活塞的直线运动可采用曲柄滑块机构来实现，但当曲柄匀速转动时，能够实现的滑块运动规律有限，而非圆齿轮副用以实现两轴间复杂的非线性传动，其传动规律由其非圆齿轮副节曲线向径决定[14]。在满足所要求的运动规律前提下，采用非圆齿轮传动可在很大程度上简化机构的复杂性，从而提高机构的综合性能。因此本文将非圆齿轮机构与曲柄滑块机构组合，运用非圆齿轮副的非匀速传动特性，实现曲柄的非匀速输入，并通过设计非圆齿轮节曲线来实现预定的滑块运动规律。

图2为脉动血流发生器非圆齿轮-曲柄滑块式驱动机构示意图。工作时，动力源驱动铰接于铰链O1上的主动非圆齿轮1做匀速转动，带动固连在铰链O2上的从动非圆齿轮2做非匀速转动，从动非圆齿轮2带动固连在其上的曲柄O2A转动，并通过连杆AB的传动，实现滑块的往复直线运动。

1.主动轮 2.从动轮 3.曲柄 4.连杆 5.滑块图2 脉动血流发生器非圆齿轮-曲柄滑块式 驱动机构示意图Fig.2 Diagram of non-circular gear slider-crank driver mechanism of pulsating blood flow generator

2 脉动血流发生器驱动机构运动学曲线方程的建立

2.1 运动学曲线的边界条件及构思

人体血流脉动法则[1]将血液流动划分为舒张期和收缩期两个阶段，舒张阶段血液流动较缓，收缩阶段血液流动加快，两阶段持续时间比例为2∶1，即脉动血液发生器输出构件回程时间与推程时间之比为2∶1。为此本文提出的脉动血液发生器驱动机构中滑块的运动规律需满足表1中的条件，设定该驱动机构一个周期时间为T，滑块最大位移量为smax，易知滑块在转向处速度大小为0，为使所设计的机构运动平稳、冲击小，设定滑块转向时加速度大小为ax、跃度值为jx。

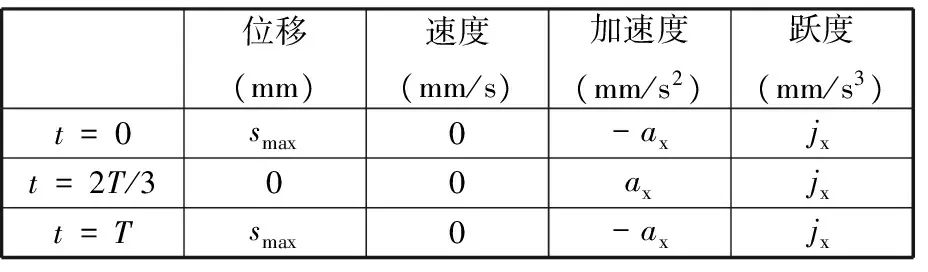
表1 脉动血流发生器驱动机构边界条件Tab.1 Boundary condition of driving mechanism ofpulsating blood generator

本文采用2段Hermite插值多项式来构建脉动血流发生器驱动机构中滑块的理想运动曲线。为使滑块运动连续，其加速度曲线必须为光滑连续曲线，但考虑到加工精度及制造费用随所采用多项式的幂次的增加而增加，本文在满足该驱动机构工作要求的情况下，选用2段三次Hermite插值多项式来对滑块加速度曲线进行拟合，然后对加速度曲线方程进行积分运算，得到滑块的速度曲线方程，再对速度曲线方程积分运算得到滑块的位移曲线方程，该加速度曲线方程对时间求一阶导数可得跃度曲线方程。

2.2 加速度方程的构建

由表1可知，所设计的非圆齿轮-曲柄滑块式驱动机构滑块运动规律按时间可分为[0,2T/3]和[2T/3,T]两个区间。

(1)当t∈[0,2T/3]，即滑块处于回程阶段时，其加速度曲线用三次Hermite多项式可表示为

(1)

(2)

(2)当t∈[2T/3,T]，即滑块处于推程阶段时，其加速度曲线方程可表示为

(3)

(4)

因此用2段Hermite三次多项式构造的滑块一个周期内加速度方程可表示为

(5)

2.3 速度方程的构建

(6)

其中，回程阶段速度方程积分常数C1=0，推程阶段速度方程积分常数C2=10axT+2jxT2。

2.4 位移方程的构建

(7)

其中，回程阶段位移方程积分常数

(8)

推程阶段位移方程积分常数

(9)

由式(8)和式(9)可知，要使所构建方程满足所设定边界条件，加速度值ax和跃度值jx需满足如下条件：

(10)

2.5 跃度方程的构建

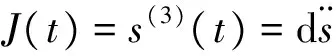
(11)

3 非圆齿轮-曲柄滑块式驱动机构运动学模型的建立

如图3、图4所示，建立以O1点为原点、水平方向为x轴、竖直方向为y轴的坐标系O1xy，建立以O2点为原点、水平方向为x′轴、竖直方向为y′轴的坐标系O2x′y′，相关参数见表2。

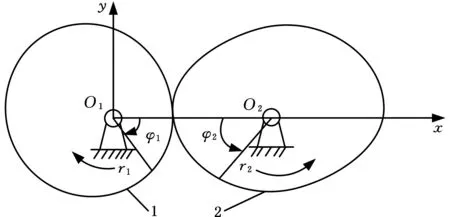
1.主动非圆齿轮 2.从动非圆齿轮图3 非圆齿轮机构Fig.3 Non-circular gears mechanism

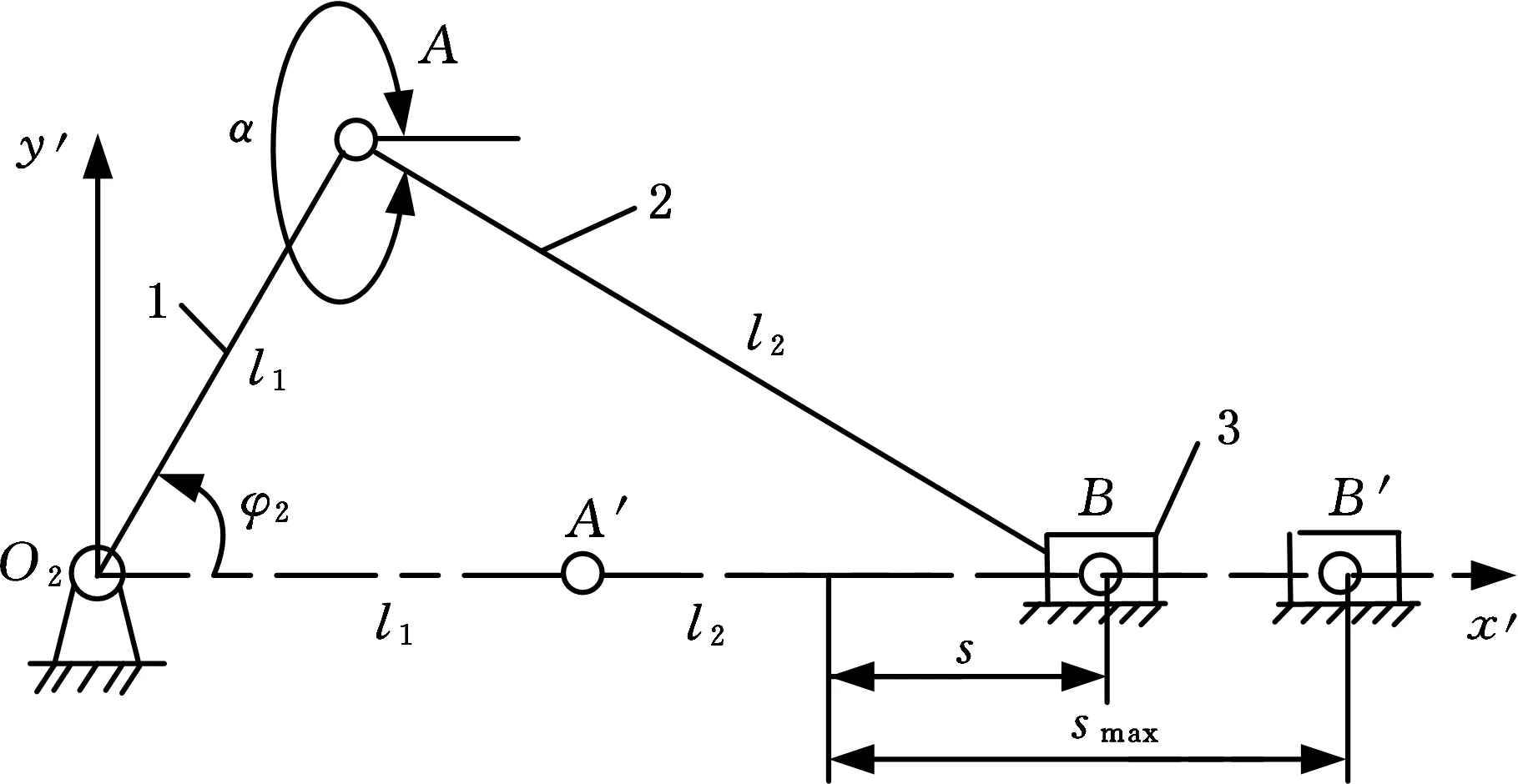
1.曲柄 2.连杆 3.滑块图4 曲柄滑块机构Fig.4 Slider-crank mechanism

3.1 非圆齿轮副运动学分析模型

表2 运动学模型相关参数Tab.2 Parameters of the kinematic model

(12)

根据非圆齿轮传动原理[14]，主动轮节曲线方程为

(13)

从动轮节曲线方程为

(14)

3.2 曲柄滑块机构运动学模型的建立

曲柄固连于非圆齿轮副的从动齿轮上，即曲柄旋转中心与从动非圆齿轮轴心为同一旋转中心，因此曲柄的角位移(和角速度)等于从动齿轮的角位移(和角速度)。为方便后续计算，设定初始时刻曲柄与水平面夹角为0，即图4中虚线位置，在坐标系O2x′y′中，由图4中几何关系可得

A点坐标：

(15)

B点坐标：

(16)

sinα=(yB-yA)/l2

由于本文驱动机构中采用对心式曲柄滑块机构，即yB=0，所以sinα=-yA/l2。

滑块位移可表示为

s=xB-(l2-l1)

(17)

由式(15)～式(17)可得

(18)

式(18)对时间t求一阶导数，得滑块速度

(19)

式(19)对时间t求一阶导数，得滑块加速度

(20)

3.3 非圆齿轮副节曲线反求设计

将第2 节构建的滑块运动学曲线方程代入第3节推导的驱动机构运动学模型，可反向求解出满足目标运动规律的非圆齿轮节曲线，具体步骤如下。

(1)整理式(18)可得从动非圆齿轮角位移

(21)

将构建的滑块位移曲线方程s(t)(式(7))代入式(21)，可求得不同时刻从动非圆齿轮角位移φ2。

(2)由式(19)可得从动非圆齿轮角速度

(22)

(23)

(4)将式(23)代入式(13)、式(14)中即可求得相应的非圆齿轮节曲线。

4 设计与分析软件及应用实例

4.1 设计与分析软件

根据前文建立的脉动血流发生器非圆齿轮-曲柄滑块式驱动机构的运动学模型，基于MATLAB开发了该驱动机构的辅助设计与分析软件，其软件界面如图5所示。

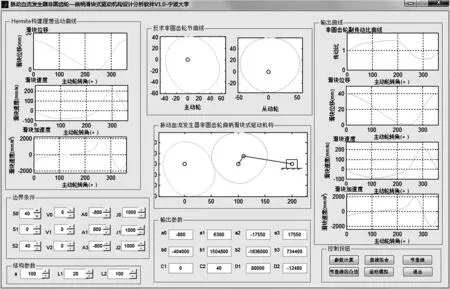
图5 脉动血流发生器非圆齿轮-曲柄滑块式 驱动机构分析设计软件Fig.5 Analysis and design software of non-circular gear slider-crank type drive mechanism of pulsating blood flow generator

该软件可根据给定的驱动机构运动学曲线边界条件构建运动学曲线方程，计算满足运动规律要求的非圆齿轮节曲线，并可进行非圆齿轮-曲柄滑块式驱动机构运动仿真和分析。

4.2 应用实例

设定该驱动机构周期T=1 s，输出构件最大位移量smax=30 mm，则主动齿轮转速为60 r/min，滑块处于行程阶段时间约为0.333 s，回程时间约为0.667 s。依据式(10)可得出该驱动机构输出机构在转角处的加速度值大小ax=1012.5 mm/s2及其相应位置的跃度值大小jx=12 150 mm/s3，则第2节中所构造的运动曲线多项式相关系数及积分常数如下。

(1)回程阶段：a0=-1012.5，a1=11 925，a2=-41 006.25，a3=41 006.25，C1=0，D1=30。

(2)推程阶段：b0=-177 187.5，b1=668 250，b2=-820 125，b3=328 050，C2=34 425，D2=-5235。

由此，采用2段三次Hermite多项式拟合而成的输出构件运动曲线及其跃度曲线见图6。

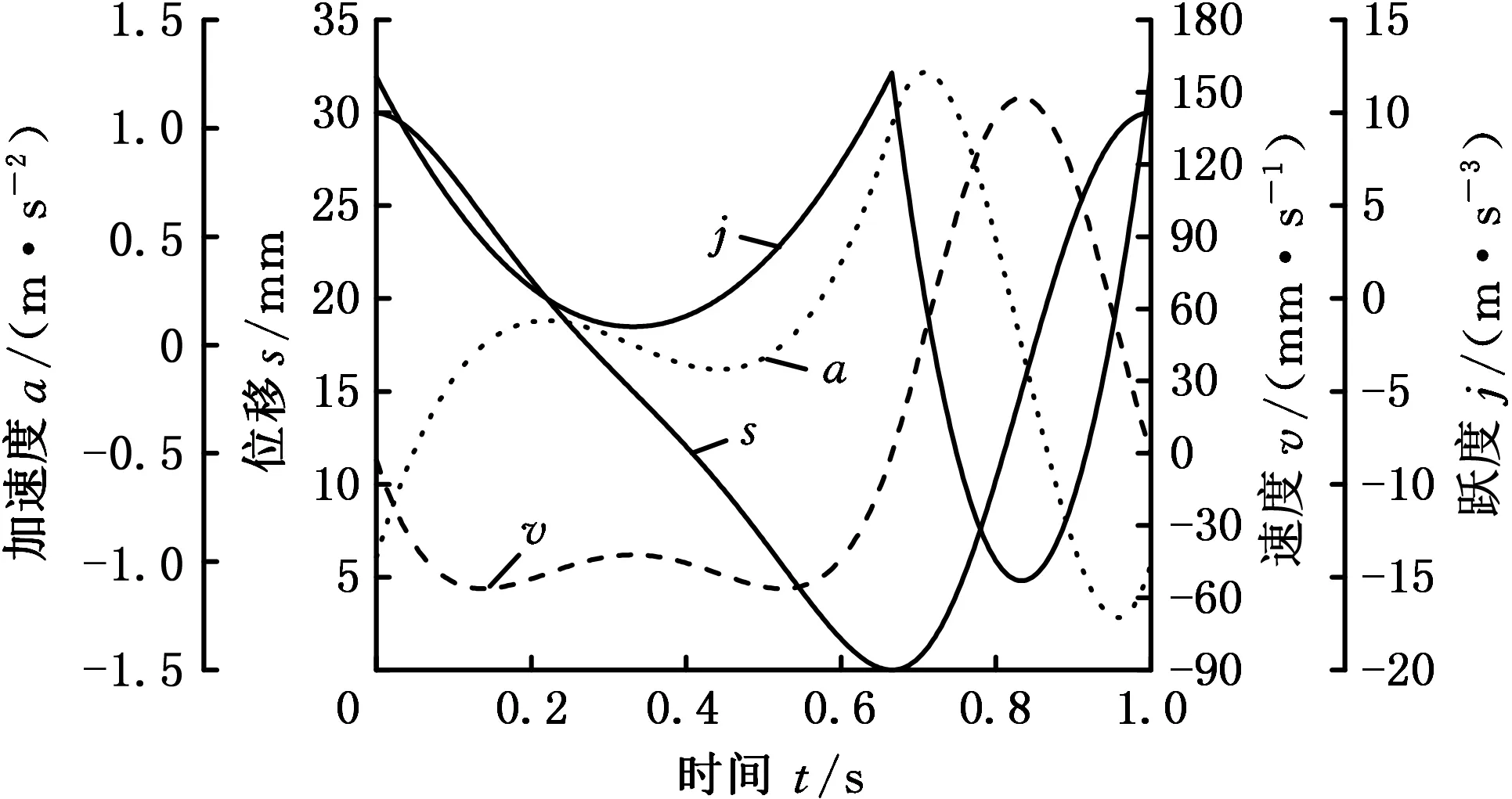
图6 Hermite多项式拟合滑块运动曲线 及其跃度曲线Fig.6 Hermite interpolation polynomials and jerk diagram of slider movement

设定该机构中l1=15 mm，l2=100 mm，a=100 mm。将上述参数输入分析软件可求得非圆齿轮副传动比如图7所示，主从动轮节曲线如图8所示。

图7 非圆齿轮副传动比函数曲线Fig.7 Non-circular gear ratio function

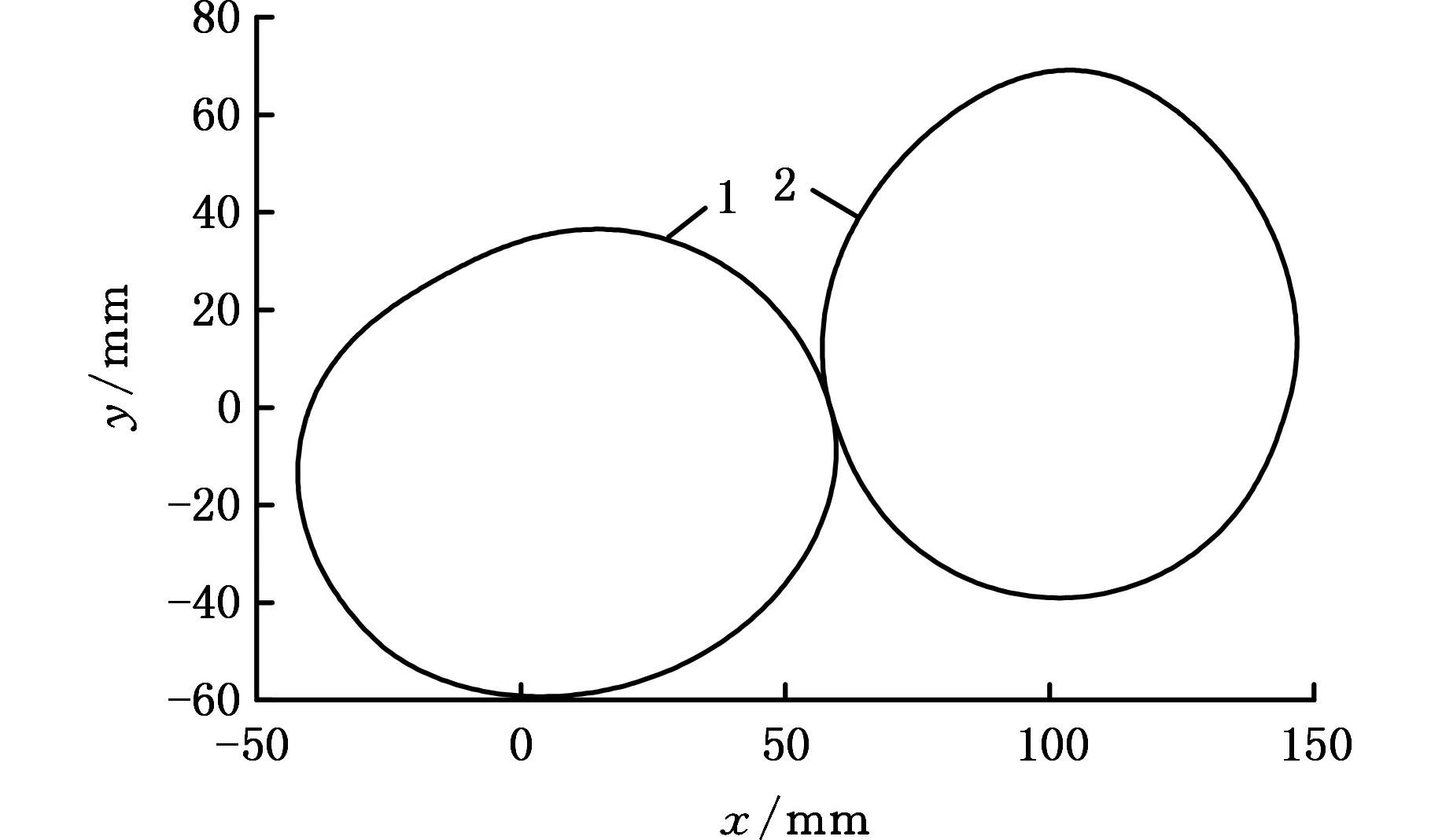
1.主动轮 2.从动轮图8 非圆齿轮副节曲线Fig.8 Computed pitch curves of non-circular gear pair

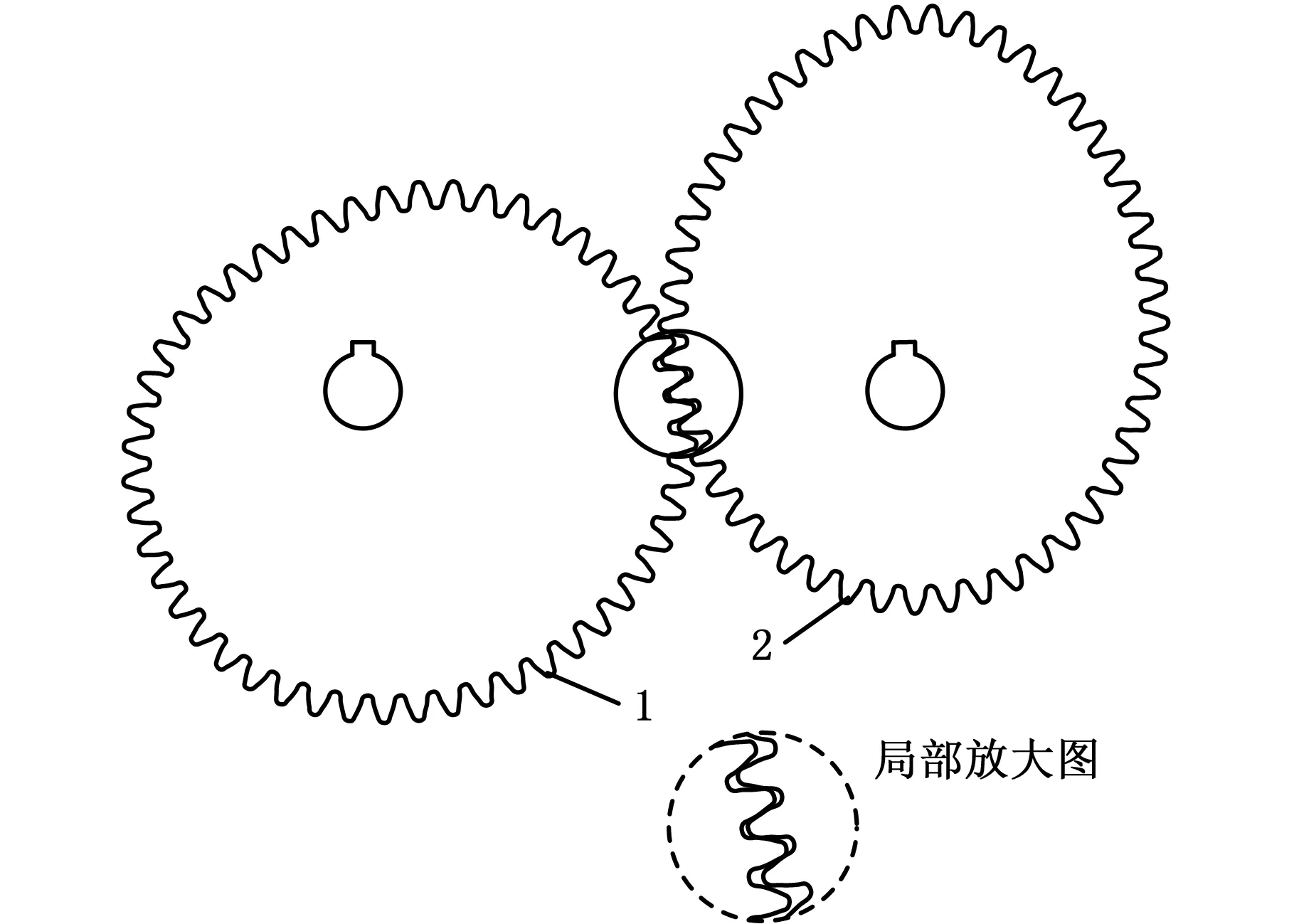
1.主动轮 2.从动轮图9 非圆齿轮副齿廓Fig.9 Tooth curves of non-circular gear pair

5 虚拟样机实验

根据实例分析得到的机构参数，基于SolidWorks三维建模软件完成该机构的实体模型的建立和虚拟装配，如图10所示。

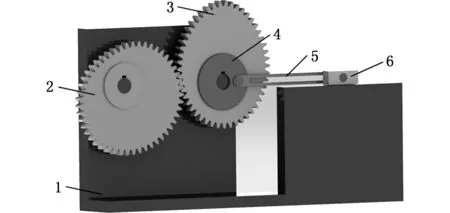
1.机架 2.主动轮 3.从动轮 4.偏心圆盘(曲柄) 5.连杆 6.滑块图10 三维实体模型Fig.10 3D solid model of mechanism

将该实体模型导入ADAMS进行虚拟样机实验。实验得到的滑块的运动学特性曲线如图11所示，仿真结果显示滑块正向速度峰值为158.365 mm/s；负向速度峰值为-70.518 mm/s，滑块加速度正向峰值为1035.633 mm/s2；负向加速度峰值为-1883.32 mm/s2，滑块位移区间为[0,30]mm。

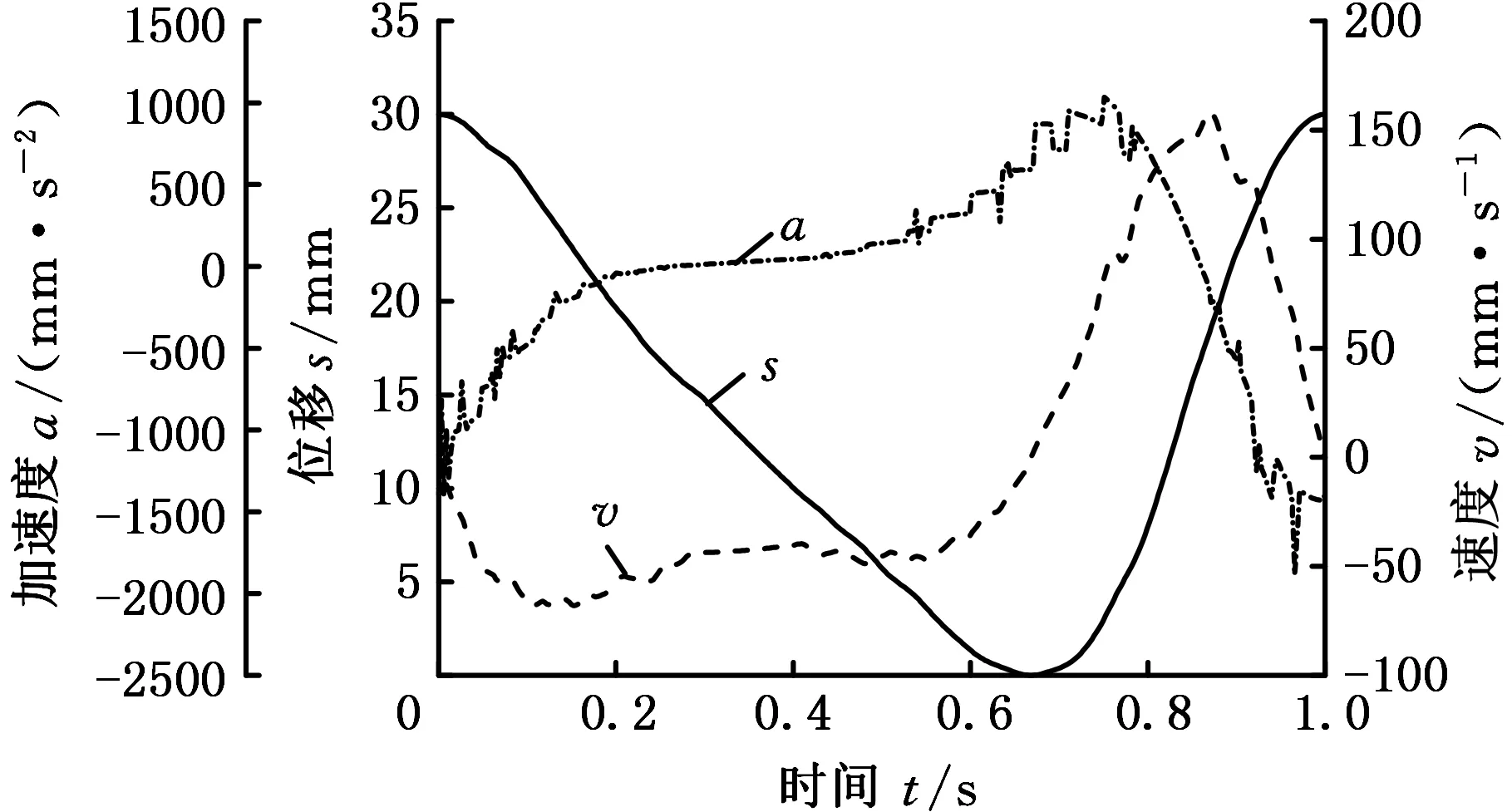
图11 运动特性曲线Fig.11 Kinetic characteristic curves

滑块位移仿真结果与用Hermite多项式拟合的位移曲线对比如图12所示，可见两曲线基本吻合，滑块到达两转折点时间基本相同，说明所设计机构能够按照预期的滑块回程阶段与推程阶段时间比为2∶1的规律运动，滑块在折返处的速度连续，加速度无较大突变，说明该机构具有良好的运动学特性。两曲线不完全重合的主要原因是虚拟实验过程中，考虑了各零件材料属性，会发生一定量的变形，而插值法拟合成的曲线是理想状态下的滑块位移，因此所构建的运动学曲线方程及所建立的运动学分析模型是正确的。

图12 理论与虚拟实验得到的滑块位移曲线对比Fig.12 A comparison between theoretical and suppositional experimental results of slider displacement

6 结论

(1)采用三次Hermite插值多项式构建滑块理想运动曲线，再代入非圆齿轮-曲柄滑块式驱动机构运动学分析模型反求出非圆齿轮副参数，此种方法适用于研究对输出构件运动规律有精确要求的机构。

(2)根据所建立的该机构数学模型，基于MATLAB软件GUI平台开发了脉动血流发生器非圆齿轮-曲柄滑块式驱动机构辅助分析设计软件，利用该软件进行参数设计，得到能够实现脉动血流的结构参数。所开发的设计软件为该驱动机构的设计分析提供了方便快捷的平台。

(3)对比虚拟样机实验和理论分析得到的结果，仿真所得输出构件运动位移曲线与理想位移曲线吻合度较高，滑块处于回程阶段与推程阶段时间比为2∶1，说明提出的非圆齿轮-曲柄滑块式驱动机构可以满足脉动血流发生器产生脉动血流的功能要求，验证了所设计机构的可行性。

[1] OKA S，蔡潮.血液脉动流[J].国际生物医学工程，1984(1)：46-51. OKA S, CAI Chao. Pulsatile Blood Flow[J]. International Journal of Biomedical Engineering， 1984(1): 46-51.

[2] 高华，胡建国，赵向东.体外循环技术临床研究和应用的进展[J].医学与哲学，2006，27(10)：59-61. GAO Hua, HU Jianguo, ZHAO Xiangdong. Development of Cardiopulmonary Bypass in Clinical Research and Application [J]. Medicine and Philosophy, 2006, 27 (10):59-61.

[3] 徐黎青.心脏手术临床用血70例探析[J].中国卫生标准管理，2015，6(29)：194-195. XU Liqing. Analysis of 70 Cases of Blood for Clinical Use of Cardiac Surgery [J]. China Health Standard Management, 2015,6 (29): 194-195.

[4] 肖颖彬.对体外循环技术的一些认识和思考[J].局解手术学杂志，2011，20(5)：471-472. XIAO Yingbin. Reflections on Techniques of Cardiopulmonary Bypass [J]. Journal of Regional Anatomy and Operative Surgery, 2011,20 (5): 471-472.

[5] 樊翔，曾繁丰.浅谈人工心肺机[J].中国医疗器械信息，2009，15(12)：34-35. FAN Xiang, ZENG Fanfeng. Discuss the Artificial Heart Lung Machine [J]. China Medical Device Information, 2009,15(12)：34-35.

[6] 钱坤喜，费青.脉动留低溶血叶轮血泵[J].中国生物医学工程学报，1990，9(2)：113-119. QIAN Kunxi, FEI Qing. Development of Pulsatile Implantable Impeller Pump with Low Hemolysis [J]. Chinese Journal of Biomedical Engineering, 1990,9(2)：113-119.

[7] 张天逸，胡兆燕.心脏辅助与替代装置中的血泵[J].中国组织工程研究，2012，16(40)：7544-7552. ZHANG Tianyi, HU Zhaoyan. Blood Pump in Heart Assistant and Replacement Devices [J]. Chinese Journal of Tissue Engineering Research, 2012, 16(40): 7544-7552.

[8] TAKEDA J. Experimental Study on Peripheral Circulation during Extracorporeal Circulation, with a Special Reference to a Comparison of Pulsatile Flow with Nonpulsatile Flow [J]. Arch. Jpn. Chir., 1960, 29:1407-1430.

[9] PARSONS R J, McMASTER P D. The Effect of the Pulse upon the Formation and Flow of Lymph [J]. The Journal of Experimental Medicine, 1938, 68:353-376.

[10] 钱晓凌，陆敢杰，卢盛.医疗设备电气安全质量控制[J].医疗卫生装备，2011,32(8)：117-119. QIAN Xiaoling, LU Ganjie, LU Sheng. Quality Control for Electrical Safety of Medical Equipment [J]. Chinese Medical Equipment Journal, 2011, 32(8): 117-119.

[11] 韩元杰，杨明.搏动型血泵驱动系统的探讨[J].中国医疗器械杂志，2009，33(1)：1-6. HAN Yuanjie, YANG Ming. A Review of Drive System for Pulsatile Blood Pump [J]. Chinese Journal of Medical Instrumentation, 2009, 33(1): 1-6.

[12] 曹云，潘钢，臧旺福，等.搏动式血泵驱动源的运动参数计算及精确实时补偿控制[J].中国医疗器械杂志，2011，35(2)：97-99. CAO Yun, PAN Gang, ZANG Wangfu, et al. Calculation of Parameters and Accurate Control with Real-time Compensator in Drive System of Pulsatile Blood Pump [J]. Chinese Journal of Medical Instrumentation, 2011, 35(2): 97-99.

[13] 孙桓，陈作模，葛文杰.机械原理 [M].7版.北京: 高等教育出版社,2006:109-138. SUN Huan, CHEN Zuomo, GE Wenjie. Theory of Machines and Mechanisms [M].7th ed. Beijing: Higher Education Press,2006:109-138.

[14] 吴序堂，王贵海.非圆齿轮及非匀速比传动 [M].北京：机械工业出版社,1997：6-8. WU Xutang, WANG Guihai. Noncircular Gear and Nonuniform Transmission [M]. Beijing: China Machine Press, 1997:6-8.

[15] 俞高红，虞佳萍，童俊华，等.一种共轭凹凸型非圆齿轮机构的设计[J].中国机械工程,2016，27(16)：2155-2159. YU Gaohong, YU Jiaping, TONG Junhua, et al. Design of a Conjugate Concave-Convex Non-circular Gear Mechanism [J]. China Mechanical Engineering, 2016, 27(16): 2155-2159.

[16] 方明辉，李革，赵匀，等.基于MATLAB的非圆齿轮副齿廓算法研究[J].农机化研究,2010,32(8)：57-60. FANG Minghui, LI Ge, ZHAO Yun, et al. Numerical Algorithm of Tooth Profile of Noncircular Gear Pair Based on MATLAB [J]. Journal of Agricultural Mechanization Research, 2010, 32(8):57-60.

[17] 陈建能，叶军，赵华成，等.高阶变性偏心共轭非圆齿轮的凹凸性及根切判别[J].中国机械工程,2014，25 (22)：3028-3033. CHEN Jianneng, YE Jun, ZHAO Huacheng, et al. Concavity and Tooth Undercutting of High-order Deformed Eccentric Conjugate Non-circular Gears [J]. China Mechanical Engineering, 2014, 25(22): 3028-3033.

(编辑 王旻玥)

Design and Analysis of Non-circular Gear Slider-Crank Mechanisms Used as Driver for PulsatingBlood Flow Generators

TAO Dehua1WANG Ying1CHEN Jianneng2RONG Quansheng1ZHOU Xian1SHU Xuedao1

1.Faculty of Mechanical Engineering and Mechanics,Ningbo University,Ningbo,Zhejiang,3152112.College of Mechanical Engineering and Automation,Zhejiang Sci-Tech University,Hangzhou,310018

A novel non-circular gear slider-crank mechanism was proposed to make pulsating blood flow generators produce stable pulsations of blood flows. The blood flow pulsations were realized by the combination of non-circular gears and slider-crank mechanisms. In order to make the designed mechanism run smoothly, the acceleration curves of the output components of the mechanism were fitted by the 2 sections of cubic Hermite interpolation polynomials under the preconditions of satisfying the law of human body blood flow pulsations, and then the equations of velocity, displacement and jerk of the output components were deduced according to the equations of the acceleration curves and the boundary conditions. The non-circular gears section curve reverse model was obtained by the output component kinematics curves equations. The 3D solid model of this mechanism was established based on mechanism parameters obtained from instance analysis and the virtual prototype test was performed after modeling. The comparison between the results of virtual simulation experiments and theoretical analyses shows that the designed mechanism may realize the pulsating blood flows according to the laws of expected, and the mechanism has fine kinematics characteristics, also verifies the correctness of the equation of kinematics curves and the kinematic analysis model.

pulsating blood flow generator; non-circular gear; slider-crank mechanism; Hermite interpolation; kinematics characteristic

2017-03-15

国家自然科学基金资助项目(51505239，51675486)；浙江省自然科学基金资助项目(LQ15E050003)；宁波市自然科学基金资助项目(2015A610099)

TH122;R318.6

10.3969/j.issn.1004-132X.2017.16.004

陶德华，男，1993年生。宁波大学机械工程与力学学院硕士研究生。主要研究方向为机构分析与综合。王 英(通信作者)，女，1989年生。宁波大学机械工程与力学学院讲师。E-mail：wangying5@nbu.edu.cn。陈建能，男，1972年生。浙江理工大学机械与自动控制学院教授、博士研究生导师。荣权升，男，1993年生。宁波大学机械工程与力学学院硕士研究生。周 贤，男，1994年生。宁波大学机械工程与力学学院硕士研究生。束学道，男，1968年生。宁波大学机械工程与力学学院教授、博士研究生导师。