SARIMA模型在湖泊水温序列中的应用

王盼盼+郭林豪+王林枝+马寨璞

摘 要：水温是影响水质的重要因素之一，为了更好地预测水温的变化趋势，为水质管理及渔业生产提供科学依据，本文以太湖梅梁湾湖区为例，选取梅梁湾1995年1月-2005年12月的水温数据，构建季节性时间序列模型，并以2006年的水温数据进行验证，结果显示了模型拟合效果较好，预测值与实测值相对误差较小，表明季节性时间序列在水温预测方面有较好的应用性。

关键词：季节性；时间序列；水温；渔业

由于自然和人为因素的影响，对湖泊的水质造成了不同形式的危害。一旦湖泊发生富营养化，就会导致藻类及其他水生生物过量繁殖，造成水质恶化。这不仅对生态环境造成一定程度的破坏，而且对渔业的生产也会产生影响。然而，水中各影响因子之间关系比较复杂并且呈非线性，各因子对影响富营养化程度的大小不一，其中水温作为影响藻类生长和繁殖的基本因子，与细胞内酶反应速率和植物的新陈代谢有密切的关系[1]。Agawin等认为水温升高对藻类数量的增加有主导作用，在其他环境条件适宜的情况下，温度每升高10 ℃都会引起藻类活动强度增加2倍[2]。所以了解水温变化趋势在一定程度上可以为预测湖泊水质提供科学依据，同时对渔业生产提供科学指导。

水温数据是随着时间的推移而记录下的一系列的数据，它们往往具有季节性和周期性。对于这种序列的数据，我们往往称为季节性序列。而处理这种序列数据的方法之一就是建立季节时间序列模型，即SARIMA模型，此模型主要应用于有长期趋势与季节性波动的时间序列的分析预测中。本文将以太湖梅梁湾湖区1995年1月-2005年12月水温数据为基础，建立季节时间序列模型，并以2006年各月水温数据为依据，对建立的SARIMA模型预测值进行验证，为水温及水质预测提供新思路。

1 SARIMA模型概述

SARIMA模型又叫季节性差分自回归移动平均模型（Seasonal Autoregressive Integrated Moving Average），存在明显的周期变化，这种周期变化主要是由于季节变化引起的。此模型的基本构成为SARIMA （p，d，q）（P，D，Q），共六个参数需要确定。其中P、D、Q主要描述季节性的变化，p、d、q用来描述去除季节性的变化，分别代表自回归、差分、移动平均。SARIMA模型在国内外不同领域均有广泛的应用，例如：Kutluk Kagan Sume等对开塞利及附近地区的电力需求应用SARIMA模型进行了预测[3]；王莹等用SARIMA模型对北京地铁进站的客流量进行了预测[4]；刘涛等将SARIMA模型应用于山东省手足口病发病趋势的研究[5]；田苗等基于条件植被温度指数，用SARIMA模型对关中平原进行了干旱预测[6]。以上模型均很好地拟合了数据趋势，预测结果与实际情况较吻合。

2 研究区概况

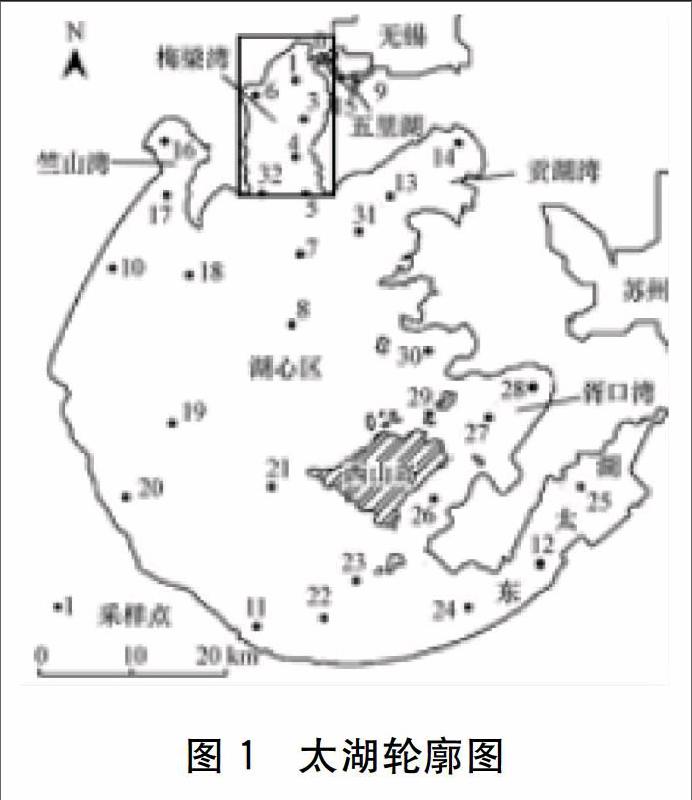
太湖是我国东部近海区域最大的湖泊，是我国第二大淡水湖泊。湖泊面积随着自然和人为因素的影响已经逐渐缩减到2 427.8 km2，位于北纬30°55'40"～31°32'58"和东经119°52'32"～120°36'10"之间。梅梁湾是太湖北部的一个湖湾，面积约129.3 km2，平均水深2.3 m，是无锡市主要水源地及旅游区。梅梁湾东北部有梁溪河、五里湖注入，西北部与武进港、直湖港有水力联系[7]。由于入湖河道及沿岸的污染影响，梅梁湾内蓝藻水华现象严重。图1为太湖区域的轮廓图，方框中的区域为梅梁湾湖区。

3 数据来源

本文选取梅梁湾监测点1995年1月-2005年12月的水温监测数据（由中国科学院太湖湖泊生态系统研究站提供）。数据为每月一次，共132个样本数据。

4 梅梁湾湖区水温季节时间序列模型建立

4.1 数据的预处理

首先我们对数据进行预处理，通过探索性分析，防止数据在建立SARIMA模型时存在由于录入错误、缺失以及不相等的观测区间或者不相关的时间等而出现的问题[8]。因为SARIMA模型是对序列相邻时期的观测值之间的相关关系进行的建模，不能应用于有缺失值的时间序列。对于数据中出现的缺失值，本文采取临近年份之间的平均值来代替。而对于间隔不等的时间序列可以用差值法来转换成等间隔的时间序列，本文中时间序列相等，为每月一次。

时间序列的确定性分析：

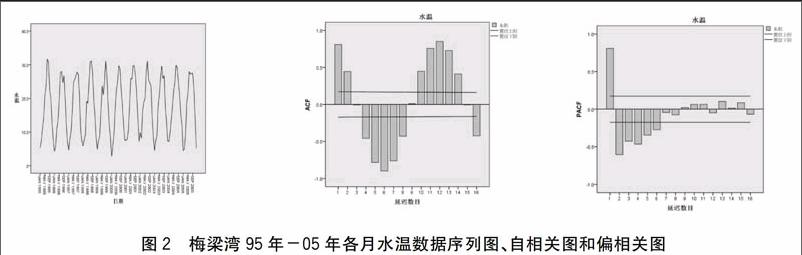
（1）对梅梁湾1995年1月-2005年12月的各月水温数据做时间序列图，如图2（左）所示，可以看出该序列存在季节性周期波动，但是趋势性并不明显。

（2）計算观测序列的样本相关系数和样本偏相关系数。在时间序列中，相邻两个时间点的观测值具有一定的相关性，即所谓的自相关；它们的相关系数则成为自相关系数（ACF）。而偏相关系数（PACF）指的是在给定中间观测值的条件下，时间序列的观测值与过去观测值的线性相关性的系数。梅梁湾样本数据的自相关函数和偏相关函数图如图2（中、右）所示，由此可以看出序列为非平稳状态，所以需要对此序列进行差分，从而转换为平稳序列，继续建立模型。

4.2 模型识别

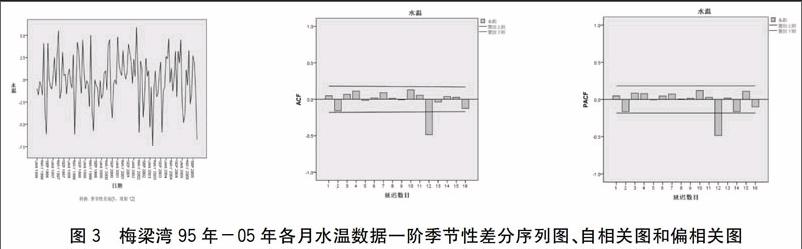
所谓差分（Difference），即是用原序列的每一个观测值减去前面一个观测值，所形成的就是对原序列的一阶差分。通过以上对梅梁湾1995年-2005年的水温数据的分析得出此序列为季节性时间序列，故需对原序列进行一阶季节性差分，从而消除其季节性因素，使序列得以平稳。差分后的序列图以及自相关和偏相关图如图3所示。一阶季节性差分后的序列图的季节性已不明显，但是自相关图和偏相关图的滞后12阶处有明显的峰值，说明此差分序列仍然存在一定周期性，故继续进行单位根检验。所得结果如图4所示，ADF值= -9.664 849，小于三个显著性水平下的值，所以拒绝原假设，此序列没有单位根，认为是平稳序列，可以建立SARIMA模型。

4.3 参数估计

模式识别之后，便可以对模型进行初步定阶。但是符合模型模式的参数并不唯一，所以要考虑到所有可能的参数值。由于一阶季节性差分后序列达到平稳状态，所以不难确定d=0，D=1。对于p，q，P，Q的可能取值，可以由低阶到高阶拟合模型，根据BIC准则来确定最终的最优模型的参数。本文经过筛选，最小的BIC的值为1.664，最优模型为SARIMA（0，0，0）（1，1，1）。该模型的统计量结果见表1，R方值为0.936，说明拟合较好，显著性的值大于0.05，表明残差错误是随机的。

4.4 模型診断与检验

根据模型SARIMA（0，0，0）（1，1，1）拟合得到的残差自相关及偏相关图见图5，从图中可以看出残差序列基本不存在相关性，位于置信区间内，可以看做白噪声序列，故本文所建立的SARIMA（0，0，0）（1，1，1）模型是比较可靠的。

4.5 模型预测结果及分析

对模型进行检验之后就可以用所建立的SARIMA（0，0，0）（1，1，1）对梅梁湾1995年1月-2005年12月的水温数据进行拟合，以及对2006年各月水温进行预测，如图6所示，从图中可以看出拟合情况与原序列较吻合。表2记录了2006年各月水温的预测值以及当年的实测值，为了更好地验证模型SARIMA（0，0，0）（1，1，1）的预测准确性，本文以相对误差的大小作为衡量标准。经计算，相对误差大都在15%以下，且误差为零的有2个，误差小于5%的有3个，误差在5%～10%的有2个，误差在10%～15%的有3个，误差在15%～20%的有1个，误差超过20%的有1个，总体来说平均相对误差为7.9%。所以本文建立的季节时间序列模型有较好的预测效果，相对误差在允许的范围内。图5 模型SARIMA（0，0，0）（1，1，1）残差序列自相关和偏相关图.

5 结论

本文对太湖梅梁湾湖区建立的季节性时间序列模型能够很好地拟合水温序列趋势，同时经过2006年实测水温数据的验证，表明SARIMA模型的预测效果较为理想，能够适用梅梁湾湖区的水温预测。

时间序列应用领域比较广泛，但是将季节时间序列应用于湖泊的管理及水质预测还不是很多，由此为研究水生态及渔业生产的科学管理提供了一种新思路。

参考文献：

[1] 田志富.基于RDA的白洋淀浮游植物群落结构动态特征分析[D].保定：河北大学，2012

[2] N S Agawin， C M Duarte， S Agusti. Nutrient and Temperature Control of the Contribution of Picoplankton to Phytoplankton Biomass and Production[J].Limnology and Oceanography，2000，45（3）： 591-600

[3] Kutluk Kagan Sumer， Ozlem Goktas， Aycan.Hepsag.The Application of Seasonal Latent Variable in Forecasting Electricity Demand as an Alternative Method[J].Energy policy，2009，37（4）：1317-1322

[4] 王莹，韩宝明，张琦，等.基于SARIMA模型的北京地铁进站客流量预测[J].交通运输系统工程与信息，2015（06）：205-211

[5] 刘涛，王显军，姜宝法，等.SARIMA模型预测山东省手足口病发病趋势[J].中国卫生统计，2013，30（05）：697-700

[6] 田苗，王鹏新，韩萍，等.基于SARIMA模型和条件植被温度指数的干旱预测[J].农业机械学报，2013，44（02）：109-116

[7] 陈鸣，陆卫鲜，郁建桥，等.太湖梅梁湾水污染及蓝藻分析计算[J].河海大学学报（自然科学版），2010，38（6）：634-638

[8] 格雷特，李洪成.时间序列预测实践教程[M].北京：清华大学出版社，2012