土压平衡盾构机多级环形刀盘设计

廖兆锦马怀祥朱齐平

土压平衡盾构机多级环形刀盘设计

廖兆锦1，2马怀祥1★朱齐平1

（1.石家庄铁道大学机械工程学院，050043，石家庄；2.中铁工程装备集团有限公司，450016，郑州//第一作者，硕士研究生）

针对盾构机施工过程中容易出现卡盘与结泥现象，设计了具有双刀盘的多级环形刀盘结构，改变了一般盾构机刀盘一体化结构，其中外环刀盘为平顶形，内环刀盘为外锥形。通过对比在锥形刀盘上安装的盘形滚刀和在平顶形刀盘上安装的盘形滚刀与岩石相互作用的力学模型，计算内环刀盘合适的外径范围和锥角区间，为今后多级环形刀盘盾构机的研发设计提供理论依据。

盾构机；多级刀盘；环形刀盘；力学模型

Author′s addressCollege of Mechanical Engineering，Shijiazhuang Tiedao University，050043，Shijiazhuang，China

土压平衡盾构机刀盘通常为一整体，与掌子面接触的土体随刀盘作同方向旋转运动。在刀盘径向，随半径的增大，刀具切削的线速度逐渐增大，在含有孤石地层容易出现刀盘中心区域卡刀盘现象，在黏土地层容易出现刀盘中心区域结泥饼现象。这两种问题是盾构施工中经常出现并难以克服的难题。

为了解决孤石卡刀盘和刀盘结泥饼的问题，需对盾构机刀盘结构进行重新设计，改变单一刀盘形式，可采用多级环形刀盘结构来解决该系列问题。多级刀盘即通过增加刀盘个数来改变原有刀盘结构，并设置内环刀盘为外锥形，增大中心区域刀盘线速度，降低盘形滚刀破岩比能，提高刀盘破碎孤石能力。本文提出一种多级刀盘设计，使得盾构机既能克服孤石地层卡刀盘，又能克服各级刀盘结泥饼现象。

1 多级环型刀盘结构

盾构机多级环形刀盘的刀盘结构由两个双环形刀盘组成，分为内环刀盘和外环刀盘。外环刀盘直径6 280 mm，内环刀盘直径2 700 mm。双环刀盘的外环与内环相分离，并且独立控制，工作时以同方向不同角速度旋转，或不同方向不同角速度旋转。在刀盘中心部分，中心刀的破碎能力提高，同时能够防止刀盘中心结泥饼、孤石卡刀盘的现象。

多级环形刀盘外环和内环机械结构如图1所示。外环刀盘和内环刀盘均由3根扭腿与刀盘主梁联接，不能安装滚刀，外环刀盘的其余3根主梁（宽度为720 mm）和副梁上可以安装滚刀和刮刀；内环刀盘完全套在外环刀盘内，后端连接法兰与外环刀盘连接法兰平齐，将通过螺栓与主轴承联接。

图1 多级环形刀盘结构

多级环形刀盘中的内环刀盘有多种类型，如平顶形刀盘和外锥形刀盘。平顶形双环形刀盘外环和内环刀盘均为平顶形；外锥形双环形刀盘外环为平顶形，内环为锥形。两者其余设计均相同（如图2所示）。

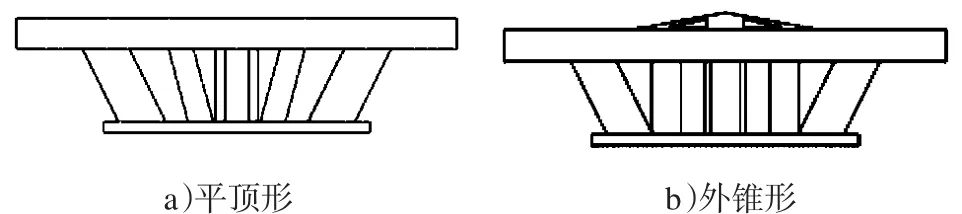
图2两种双环刀盘结构形式

图3 所示为双环形刀盘盘形滚刀安装示意图。外环刀盘为平顶形，则在外环平顶形刀盘上安装的盘形滚刀径向方向与盾构机轴线平行；内环刀盘设置为外锥形，则在刀盘上安装的盘形滚刀径向方向与盾构机轴线存在一定夹角。无论刀盘是平顶形还是外锥形，刀盘上的盘形滚刀与刀盘均是正安装，只因刀盘存在锥角而导致盘形滚刀与盾构机轴线方向存在一定的角度，该角度等于内环刀盘的锥度。

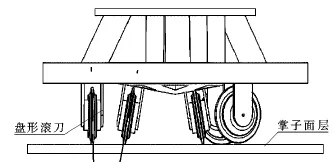
图3 双环形刀盘盘形滚刀安装简图

2 外锥形刀盘上安装盘形滚刀破岩模型

如图4所示的外锥形刀盘上，在盘形滚刀作用下岩石发生破坏而产生α滑移线和β滑移线。当岩石平面发生塑性变形时，在塑性区域内的各点其应力状态都满足屈服条件。作用区域任意一点处的两个最大剪应力方向相互垂直，且大小相等。将塑性变形区域内各点处最大剪应力的方向连接起来，绘制成的连续曲线即是二族正交曲线。一族称为α族，另一族称为β族。此正交曲线便称为滑移线网络曲线。

在图4上方的应力q是假设的盘形滚刀作用于岩石表面上的力，由于对称且是均布力，可只考虑XOY坐标系第一象限区域。

根据塑性理论，在边界OB上，当盘形滚刀作用下的岩体进入塑性状态时，可表示为：

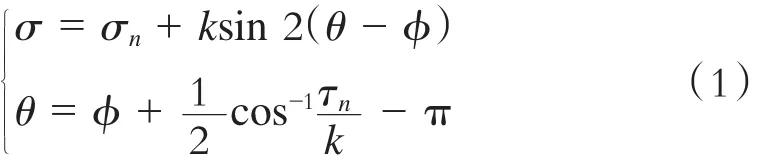
式中：

σ——作用点处的平均应力；

σn——作用点处边界上的法向应力；

k——屈服条件；

φ——边界OB的乘线与OX轴正面之间的夹角；

θ——边界OB上作用点处α滑移线切线正向与X轴正向的夹角；

τn——边界OB上作用点处的剪应力。

首先分析X轴正向OB边的受力状态。因OB边在均布应力q的作用下，有σn=-q；τn=0；对于Mises理论，k=，对于Tresca理论，k=；σS为材料的屈服强度，φ=。将上述参数代入式（1）中得：

B点既是边界上的点，B又是β滑移线上的点，根据Hencky H方程可得

式中：

Cβ，B——B点的Cβ，沿任一条β线Cβ为常数；

σB——B点的平均应力；

θB——B点的θ。

在边界OA上，σn=τn=0，在△OCB区域，α滑移线为正向，则在边界OA上存在

式（4）中δ为A点既在边界OA上，又在β滑移线上，根据Hencky H方程可得

由于Cβ，A=Cβ，B，可得

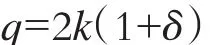
此即为盘形滚刀外倾安装破岩时的极限载荷计算公式。

3 平顶形刀盘上安装盘形滚刀破岩模型

4 两种刀盘的盘形滚刀破岩效能分析

盘形滚刀的破岩效能一般用比能Sen来衡量，即盘形滚刀破碎单位体积岩石所消耗的能量。

式中：

W——破碎V体积岩石所消耗的能量；

V——破碎岩石的体积。

对于在盘形滚刀破岩的一维模型中，破碎岩石的体积与所消耗的能量可以按式（7）计算：

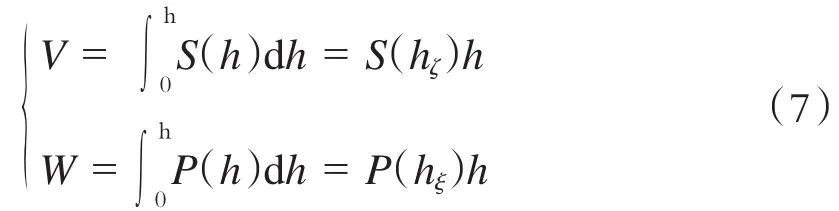
式中：

h——盘形滚刀切入岩石的深度；

P（h）——盘形滚刀切深为h时，作用在滚刀上的力；

hζ、hξ——（0，h）区间的中点；

S（h）——滚刀作用下深度为h的平面所截岩石的面积。

将式（7）代入式（6）中，得Sen=，可知比能亦可表示为单位面积下滚刀对岩石平面的作用力，即单位极限载荷。假设岩石材质相同，盘形滚刀切深深度也相同，则盘形滚刀的破岩效能可近似用盘形滚刀破岩的极限载荷来衡量，即

因此，针对盘形滚刀破碎单位面积岩石消耗比能而言，外锥形刀盘上安装的盘形滚刀比平顶形刀盘安装盘形滚刀消耗比能的减少量S△Sen为：

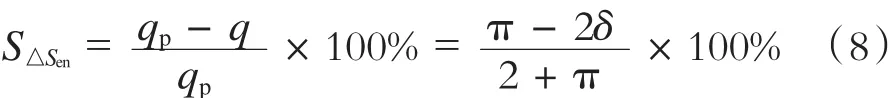
由式（8）可以看出，比能减少量为线性减函数。从理论上说，δ越小则比能减少量越少，节省能量越多。根据盘形滚刀切削岩石的实际情况，δ最小值为：

式中：

Ri——外锥形刀盘上盘形滚刀的破岩轨迹圆半径；

h——盘形滚刀切深；

r——盘形滚刀半径。

在盘形滚刀半径一定的情况下，δ存在最小值，随着盘形滚刀半径的增大，δmin增大，即盘形滚刀倾斜角度减小，如图5所示。随着切深的增加，δmin图形重合，大小基本不变，所以在其他条件不变情况下盘形滚刀切深对其破岩比能减少量没有影响。

将图5数据代入式（8），得到不同轨迹圆半径下比能曲线（见图6）。

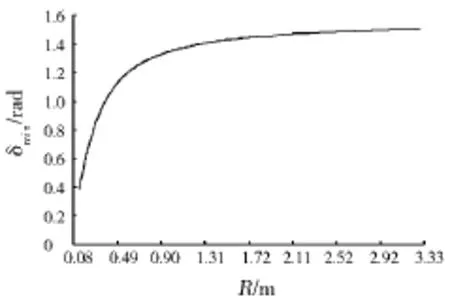
图5 盘形滚刀不同轨迹圆下最小δ

图6 盘形滚刀不同轨迹圆半径下比能曲线

从图6中可以得出，轨迹圆半径越小，比能减小量越大，因此，将内环刀盘设置为外锥形，半径小且易于制造，破碎岩石能力强且耗能低。

从图5和图6可知，半径R≤0.9 m时，δmin随R的增加急剧增加，比能减小量则急剧减小；0.9 m≤R≤2.1 m时，δmin和比能减小量变化趋于平缓，δmin范围为1.34 rad≤δmin≤1.46 rad，即76.78°≤δmin≤83.65°；随着半径的继续增加，δmin达到最大值90°。因内环刀盘外锥形的锥度为一固定值，所以δmin应在平缓区域选取，即6.35°≤γman≤13.22°。取γman= 10°，则δmin=1.39 rad（=80°），比能减少量为5.838%。

5 结语

本文提出土压平衡盾构机的多级环形刀盘结构设计，其外环刀盘为平顶形，内环刀盘为外锥形，两环形刀盘的法兰盘平行，与双环驱动主轴承联接。

在一定切深条件下，锥形刀盘半径小的滚刀破岩效率高，因此，设计内环刀盘为外锥形，外环刀盘为平顶形。通过对比平顶形刀盘上安装的滚刀和锥形刀盘上安装的滚刀破岩效能，确定锥形刀盘半径为0.9 m≤R≤2.1 m、锥度为6.35°≤γman≤13.22°是最为适宜的。最终设计多级环形刀盘内环半径为1.7 m，内环刀盘锥角为10°。

［1］张照煌，户秀妹，孟亮.盘形滚刀破岩效能理论分析［J］.应用基础与工程科学学报，2012，20（增刊1）：199-205.

［2］ROXBOROUGH F F，PHILLIPS H R.Rock excavation by disc cutter［J］.International Journal of Rock Mechanics and Mining Sciences，1975，12（12）：361-366.

［3］纪昌明，张照煌，叶定海.盘形滚刀刀间距对岩石跃进破碎参数的影响［J］.应用基础与工程科学学报，2008，16（2）：255-263.

［4］尹超旅.日本隧道盾构新技术［M］.武汉:华中理工大学出版社，1999.

Design of Earth Pressure Balance Shield with Multi-stage Ring Cutter-head

LIAO Zhaojin，MA Huaixiang，ZHU Qiping

Aiming at shield lining mud phenomenon in tunnel construction，a multi-stage ring cutter-head is designed，which has the outer flat cutter-head and the inner cone cutter-head. By comparing the mechanical model of the respective interactions between cutter and rock，the suitable diameter of the inner cutter-head and the angle range of cone cutter-head are calculated to provide a theoreticalbasis for future shield design.

shield；multi-stage cutter-head；ring cutterhead；mechanical model.

U455.3+1

10.16037/j.1007-869x.2017.08.027

2015-11-15）

*马怀祥为本文通讯作者