基于谐波小波和去趋势波动分析的摩擦振动信号研究
2017-08-30李精明魏海军魏立队杨智远
李精明, 魏海军, 魏立队, 杨智远, 刘 冲, 刘 竑
(1. 上海海事大学 商船学院, 上海 201306; 2. 大连海事大学 轮机工程学院, 大连 116026)
基于谐波小波和去趋势波动分析的摩擦振动信号研究
李精明1,2, 魏海军1, 魏立队1, 杨智远1, 刘 冲1, 刘 竑1
(1. 上海海事大学 商船学院, 上海 201306; 2. 大连海事大学 轮机工程学院, 大连 116026)
为实现摩擦振动信号的降噪和摩擦振动信号特征提取,在往复式摩擦磨损试验机上进行了摩擦副摩合磨损试验。应用谐波小波对获得的非线性、非平稳的摩擦振动信号进行分解,实现摩擦振动信号的降噪。应用去趋势波动分析算法对摩擦振动信号进行分析,获得不同阶数下的Hurst指数,判别数据序列的属性及其趋势增强的程度。研究结果表明,随着磨合磨损试验的进行,摩擦振动信号的标度指数呈现逐渐增大的变化趋势,去趋势波动分析算法能够实现摩擦振动信号特征提取,摩擦振动信号的标度指数变化能够用于摩擦副的磨合磨损状态监测和识别。
谐波小波; 去趋势波动分析; 标度指数; 摩擦振动
摩擦振动是机械运动摩擦副在摩擦磨损过程中产生的现象,蕴含着许多反映系统摩擦学特征和摩擦状态的信息[1]。摩擦学系统的输出信息包括摩擦振动、摩擦力矩、摩擦因数、磨粒形貌、磨损表面形貌[2]等。许多学者从这些摩擦学参数来研究摩擦副摩合磨损状态以及摩擦副相关的机械故障诊断,但通过摩擦力矩、摩擦因数、磨损表面形貌来提取摩擦学特征存在一定的困难[3]。而通过磨粒形貌来分析则程序繁琐和低效,且分析结论与研究人员的经验有密切关系[4]。机械设备的摩擦振动信号可以通过加速度传感器获得,可在机械设备运行的情况下实时在线采集,因此可以通过提取机械设备的摩擦振动信号的特征来实时监测机械设备摩擦副的状态。亦可通过分析摩擦副相关机械各状态摩擦振动信号的特征,实现摩擦副相关机械的故障诊断。
谐波小波(Harmonic Wavelet, HW)理论[5]是Newland于1993年提出的信号处理方法。谐波小波是一种复小波,在频域紧支,有明确的函数表达式,谐波小波函数具有频域盒形紧支谱特性及良好的相位定位能力,在信号分解过程中数据信息量不变,频域成分不相交,在频域具有良好的细化能力,可以将信号细分到任意频段,广泛应用于信号去噪[6],机械故障诊断[7]地震波分析[8]等领域。基于分形自相似理论发展起来的去趋势波动分析(Detrended Fluctuation Analysis, DFA)是Peng等[9]生物物理学家于1994年探测DNA内部分子链的相关可能性程度时首先提出的。通过对信号累积和的分段去趋势运算来突出信号中的弱相关成分,能够检测非平稳信号中的长程相关信息,被成功应用到信号去噪[10]、故障诊断[11]、医学数据分析[12]等领域,取得很好的效果。
通过摩擦振动信号来进行摩擦副状态识别和摩擦磨损行为研究的核心是摩擦振动信号的特征提取。有学者应用时频谱图[13]、谐波小波、奇异值分解[14]、混沌吸引子[15]、多重分形[16]等提取摩擦振动信号的特征,取得了较好的效果。本文针对以船用柴油机缸套和活塞环为材质的摩擦副摩擦磨损试验过程中获得的摩擦振动信号进行谐波小波分解,重构获得降噪的摩擦振动信号。应用去趋势波动分析算法对降噪后的摩擦振动信号进行分析,得到去趋势波动分析谱图及不同阶数下Hurst指数,实现特征参数对摩擦副摩擦磨损状态的表征,为基于摩擦振动信号的摩擦副状态识别和摩擦磨损行为研究提供了新的方法。
1 分析方法
1.1 谐波小波算法
摩擦振动信号振幅小、能量微弱,常规的短时傅里叶变换、魏格纳维尔分布会因为摩擦振动信号的谱峰微弱而不易分辨。谐波小波(Harmonic Wavelet, HW)是Newland提出的信号处理方法,具有频域盒形紧支谱特性及良好的相位定位能力,能有效提取信号中的奇异成分。图1为信号采用谐波小波变换后的频域分布。作为谐波小波变换的拓展,谐波小波包变换可以将信号分解到任意频段,获得信号所有的低频分量和高频分量,准确地显现微弱信号。
在谐波小波分析过程中,设信号的最高分析频率为fh,则第j(j=1, 2, 3,…)层频段的带宽B可以表示为:
B=2-jfh
(1)
s为频段数,分析频带的上限m和下限n分别为:
m=sB
n= (s+1)Bs=0,1,2,…,2j-1
(2)
根据谐波小波包变换原理,摩擦振动信号的谐波小波包变换过程如下:
(1) 根据摩擦振动信号的特点确定谐波小波包的分解层数,确定频带的上下限m,n;
(2) 计算信号的离散时间傅里叶变换;
(3) 计算m,n确定尺度下的频域;
(4) 求离散傅里叶逆变换FFT,对所需频段的信号进行时域分析。
1.2 去趋势波动分析理论及算法
DFA是一种计算长程相关性的方法,能定量地描述时间序列标度不变性,可用于非静态、非平稳数据分析。与重标极差法(Rescaled range analysis)相比[17],DFA 分析法消除了序列的局部趋势,避免了将时间序列的短程相关、非平稳性虚假地检测为长程相关性。

图1 谐波小波包分解的频域分布图
对于一个非平稳时间序列{xi}(i=1,2,…,N),应用DFA方法分析的主要步骤如下:
(1) 计算时间序列{xi}(i=1,2,…,N)的离差序列Y(i):

(3)
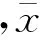
(2) 把Y(i)等分成Ns个不重叠的等时间长度s的区间,其中Ns=[N/s](即取整数)。由于序列长度并不总是时间长度s的倍数,使得有小部分序列数据剩余. 因此,对Y(i)的进行逆序的同样操作,这样共有2Ns个等长度的区间。
(3) 对每个区间v,用最小二乘法拟合数据,得到局部趋势,拟合多项式的阶数可以是一次的、二次的、更高次的,拟合的阶数反映了“趋势”被消除的程度,阶数越高,“趋势”消除的效果越好,但计算时间也相应增加。滤去该趋势后的时间序列记为Ys(i),表示原序列与拟合值之差,即:
Ys(i)=Y(i)-Pv(i)i=1,2,…,N
式中,Pv(i)是第v区间的拟合多项式。拟合多项式采用线性、二次、三次,可以是更高阶m的多项式,则分别记为DFA1,DFA2,DFA3,…,DFAk等。显然k阶的DFA 滤去了累积离差中的m阶趋势成分以及原始序列中的k-1阶趋势成分。
(4) 计算每个区间滤去趋势后的方差,以区间(v=1,2,…,2Ns)为例,进行k阶多项式拟合:
yv(i)=a1ik+a2ik-1+…+ak+1k=1,2,…
(4)
对于区间(v=1,2,…,Ns):
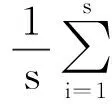
(5)
对于区间(v=N+1,N+2,…,2Ns)
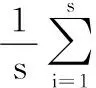
(6)
(5) 确定数据序列的q阶波动函数:
(7)
(6) 通过分析双对数坐标图s~Fq(s)的关系,确定波动函数的标度指数h(q),即存在幂率关系:
Fq(s)∝sh(q)
(8)
不同阶数q下的Hurst指数即标度指数h(q),可考察数据DFA波动函数的标度行为,通过标度不变性来刻画时间序列的长程相关特性,即可通过数据序列不同阶数q下的Hurst指数数值来判别数据序列的属性及其趋势增强的程度。
1.3 标度指数的含义
标度指数h(q)存在于一定标度区间,可用于表征数据序列的相关性,能将时间序列区分为随机序列与非随机序列。q为2时,对于一个时间序列[18]:
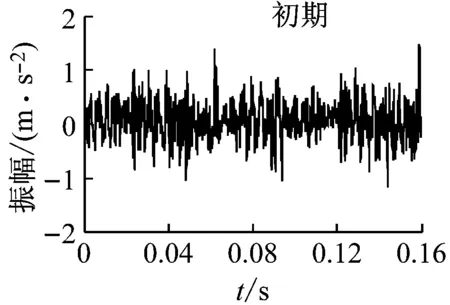
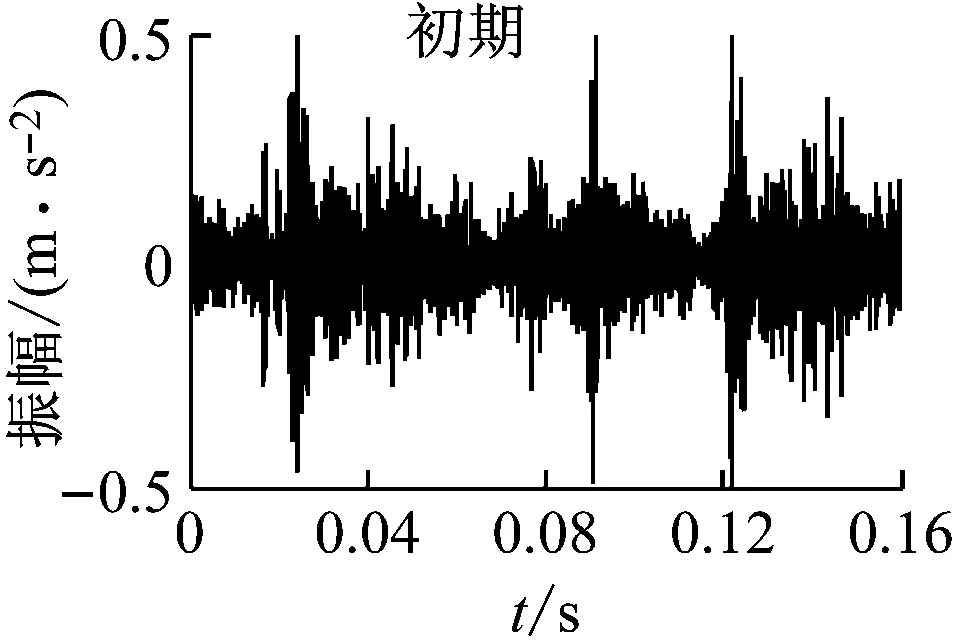
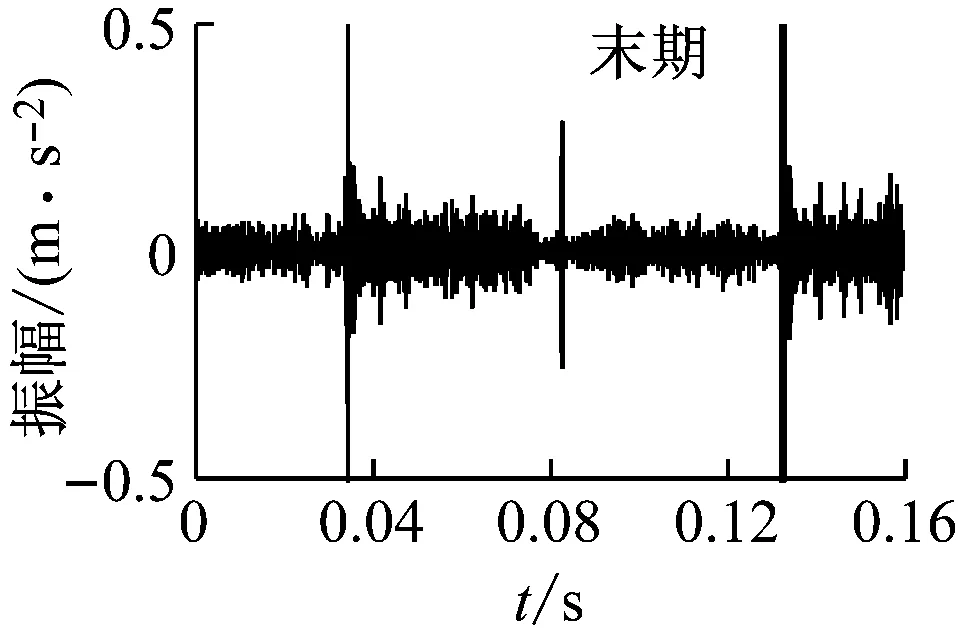
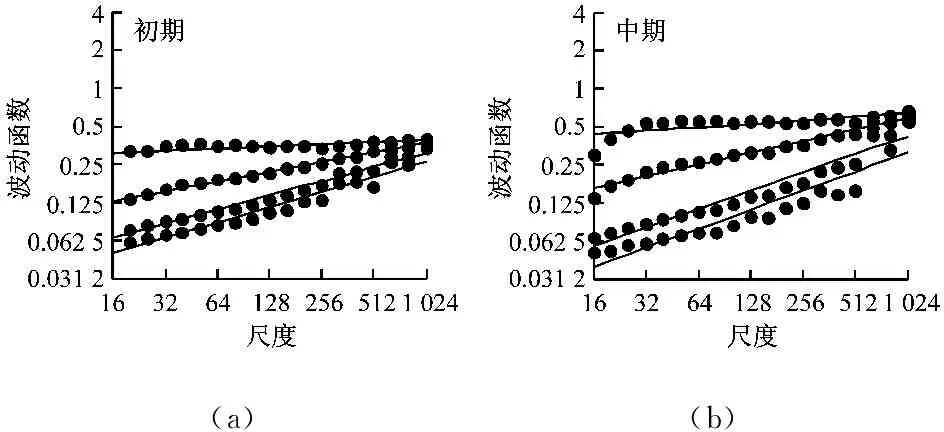
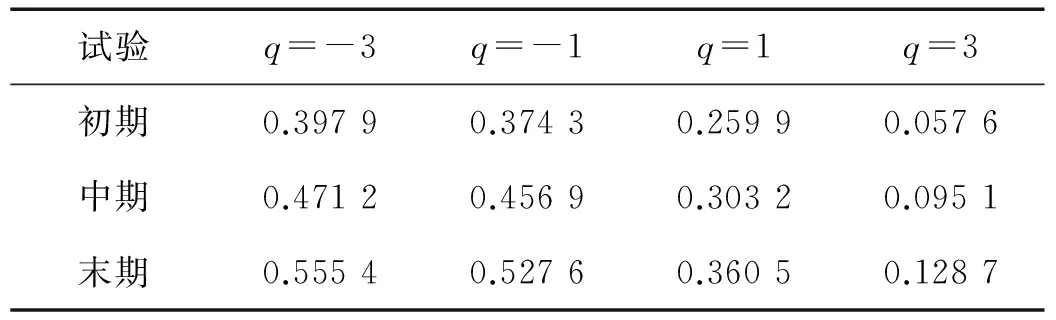
当0 当h(q)=0.5时,标志着所研究的数据序列是一个随机序列,即过去的增量与未来的增量不相关,序列具有标度不变性。 当0.5 2.1 试验方法与材料 摩擦副摩擦磨损试验的设备采用CFT-I型摩擦磨损试验机,图2为该试验机的原理。 图2 CFT-I型摩擦磨损试验机原理图 销试样和盘试样为采用线切割方法从船用柴油机的活塞环和缸套上截取。销试样固定在主轴下端部,盘试样固定在台架上,电机驱动的偏心轮连杆机构使台架和盘试样作往复运动。载荷由加载机构经销试样施加于盘试样,摩擦振动信号采用美国压电公司生产的356A16型三轴加速度传感器来测量,灵敏度为100 mV/g,量程为±50 g,检测位置在盘试样下方。销试样材质为合金铸铁,主要成分为Fe、C、Si、Mo、P等,硬度HV600~680,原始表面粗糙度Ra=0.687 μm,截面尺寸3 mm×4 mm。盘试样接触表面为弧面,材质为合金铸铁,主要成分为Fe、C、Si、Mn、P等,硬度HV320~420,原始表面粗糙度Ra=1.641 μm,尺寸φ30 mm×10 mm。施加的试验力为50 N,驱动电机转速为600 r/min,销试样-盘试样相对运动的平均速度为0.1 m/s,试验时间为480 min。润滑方式为滴油润滑,润滑介质为Mobilgard 412船用润滑油,黏度141 cSt(40 ℃)。 2.2 摩擦振动信号的采集 摩擦振动信号的采集装置为比利时LMS公司生产的SCADAS(Supervisory Control and Data Acquisition System)型前端数据采集系统,采样频率25 600 Hz,采样点数4 096。采集的数据每0.16 s自动生成一个文本文件,存入计算机。 图3 摩擦振动信号的时域波形 图3为摩擦磨损试验过程中,传感器在初期、中期、末期采集的摩擦振动信号时域波形,即对于试验获得的数据,在第1 min、240 min、480 min附近各选取一个0.16 s的数据。从图3可以看出,所获得的摩擦振动信号是非线性、非平稳信号,信号波动复杂,无规律可循,微弱的摩擦振动信号堙没于背景噪声之中,需要去噪才能正确提取摩擦振动信号特征。 3.1 摩擦振动信号的谐波小波降噪 应用谐波小波实现摩擦振动信号的降噪,文献[5]指出摩擦振动信号的特点是振幅小、频率高,其中蕴含着有价值的信息。文献[14]应用谐波小波包变换对摩擦振动信号进行降噪,提取能够反映系统摩擦学特征和摩擦状态的摩擦振动信号,指出低频信号不含有反映摩擦磨损状态的摩擦振动信号,验证5 000~6 000 Hz的摩擦振动信号能够反映摩擦副摩擦磨损状态。 本文应用谐波小波,将采集的摩擦振动信号分解成7层64个频带,带宽度为100 Hz,重构第51~60频带,降噪后的摩擦振动信号时域波形见图4。从图4可以看出,降噪后摩擦振动信号幅值显著减小,周期成分减弱,摩擦振动的冲击信息清晰出现。随着磨合磨损试验的进行,摩擦振动信号的振幅呈现减小的变化趋势。 图4 重构的摩擦振动信号时域波形 3.2 摩擦振动信号的去趋势波动分析 应用去趋势波动分析算法分析去噪后的摩擦振动信号,对试验初期的摩擦振动信号,当尺度s取16,阶数q分别取-3,-1,1,3时,分析得到的波动函数如图5所示。从图中可以看出,不同阶数对信号的小振幅和大振幅有不同的分辨能力。阶数为负时,波动函数敏感地反映摩擦振动信号的小振幅变化,阶数为正时,波动函数敏感地反映摩擦振动信号的大振幅变化。可以通过不同阶数下的波动函数值来考察摩擦振动信号的振幅分布情况。 图5 摩擦振动信号的q阶波动函数 图6(a)、6(b)、6(c)所示为摩擦磨损试验初期、中期、末期摩擦振动信号应用去趋势波动分析,在不同尺度s、不同阶数q下的波动函数值,在某一阶数q下,波动函数的回归线斜率即标度指数h(q)。从图6(a)、6(b)、6(c)可以看出,不同阶数q下的波动函数值在小尺度较大尺度更为明显。由于小尺度能够更好地嵌入数据的局部周期,因此小尺度能够更明显地区分数据局部周期的大波动和小波动。随着磨合磨损试验的进行,图6(a)、6(b)、6(c)呈现出渐进的变化规律,表现在波动函数的回归线斜率的变化。图6(d)为摩擦磨损试验初期、中期、末期摩擦振动信号在不同阶数q下的Hurst指数即标度指数h(q),随着磨合磨损试验的进行,标度指数h(q)呈现增大的趋势。 (a)(b) (c)(d) 图6 摩擦振动信号的幂率关系谱图 Fig.6 Power-law relationship of frictional vibration signals 表1为摩擦振动特征信号的不同阶数q下的Hurst指数即标度指数h(q)。从表1可以看出,随着磨合磨损试验的进行,标度指数h(q)呈现增大的趋势变化,表明摩擦磨损试验获得的摩擦振动信号是反持久性数据序列,摩擦振动未来的趋势表现为与之前的相反。摩擦振动信号回归线的斜率呈现逐渐增大的变化,表明反持续性逐渐较小,数据序列的突变跳跃逆转性趋于缓和,表征摩擦副的摩擦磨损逐渐趋于稳定。 表1 摩擦振动特征信号的q阶Hurst指数 3.3 机理分析 摩擦振动信号标度指数的变化与摩擦副磨合磨损过程中磨损表面变化密切相关。摩合磨损试验摩擦副磨合初期,摩擦副表面粗糙度较大,摩擦副往复运动过程中产生的能量较大,摩擦振动信号剧烈,摩擦振动的主峰明显,平均振幅较大,摩擦副磨损过程处于不稳定的状态。随着磨合磨损试验的进行,摩擦副表面粗糙度逐渐减小。磨合磨损试验初期的摩擦振动信号标度指数数值最小,反持续性最强。随着磨合磨损试验的进行,摩擦副表面的粗糙度逐渐下降,激发的摩擦振动也减弱,磨合过程摩擦表面消耗的能量减弱,摩擦磨损逐渐趋于稳定,标度指数数值增大。第240 min时,盘试样粗糙度从最初的1.641 μm降至1.263 μm,激发的摩擦振动强度减小,振幅明显减小,主峰减少,摩擦振动信号的变化表明磨合过程损耗的能量减小,摩擦磨损趋于稳定。在磨合磨损试验的中后期,标度指数进一步增大,摩擦磨损逐渐进入稳定磨损阶段,盘试样表面粗糙度进一步减小为1.093 μm,摩擦副表面粗糙度减小的幅度减弱,表面磨损轻微,激发的摩擦振动减弱。摩擦副进入稳定磨损状态,摩擦振动主峰不明显,平均振幅减小,摩擦振动标度指数数值增大,反持续性减弱。 上述分析表明,标度指数能够参数化摩擦振动信号的特征。摩擦振动信号去趋势波动分析幂率关系谱图及其参数能体现摩擦振动的特征,反映摩擦副摩合磨损过程中所处的摩擦振动状态。 摩擦振动蕴含着反映系统摩擦学特征和摩擦状态的信息,本文利用谐波小波和去趋势波动分析研究摩擦副摩合磨损过程中的摩擦振动信号,结论如下: (1) 应用去趋势分析算法能有效地分析摩擦振动信号的非线性特征,反映摩擦副摩合磨损过程中摩擦振动渐变过程,可以用摩擦振动信号去趋势波动分析幂率关系谱图及其参数表征摩擦振动信号的特征。 (2) 去趋势分析标度指数能够参数化摩擦振动信号的特征,随着磨合磨损试验的进行,摩擦振动信号的标度指数呈现逐渐增大的变化趋势。 [1] 葛世荣,朱华. 摩擦学复杂系统及其问题的量化研究方法[J]. 摩擦学学报,2002, 22(5): 405-408. GE Shirong, ZHU Hua. Complicate tribological system and quantitative study methods of their problems[J]. Tribology, 2002, 22(5): 405-408. [2] ZHU Hua, GE Shirong, CAO Xucheng, et al. The Changes of fractal dimensions of frictional signals in the running-in wear process[J]. Wear, 2007, 263(7): 1502-1507. [3] SUN Di, LI Guobin, WEI Haijun, et al. Investigation on frictional vibration behavior of tribological pairs under different wear states[J]. Journal of Tribology, 2015, 137(4): 74-81. [4] MACIAN V, PAYRI R, TORMOS B, et al. Applying analytical ferrography as a technique to detect failures in diesel engine fuel injection systems[J]. Wear, 2005, 260(2):562-566. [5] 李国宾,任宗英,王宏志,等. 摩擦振动信号谐波小波包特征提取[J]. 摩擦学学报,2011, 31(5): 452-456. LI Guobin, REN Zongying, WANG Hongzhi, et al. Characteristics extraction of friction vibration singal using harmonic wavelet packet transforms[J]. Tribology, 2011, 31(5): 452-456. [6] 李舜酩,徐庆余.微弱振动信号的谐波小波频域提取[J].西安交通大学学报,2004, 38(2):51-55. LI Shunming, XU Qingyu. Harmonic wavelet extraction for weak vibration signal in frequency domain[J]. Journal of Xi’an Jiaotong University, 2004, 38(2): 51-55. [7] 李方,李友荣,王志刚.谐波小波时频图在齿轮故障诊断中的应用[J]. 振动与冲击,2007, 26(3): 128-134. LI Fang, LI Yourong, WANG Zhigang, Harmonic wavelet time-spectrum plot with applications in gear fault diagnosis[J]. Journal of Vibration and Shock, 2007, 26(3): 128-134. [8] CECINI D, PALMERI A. Spectrum-compatible accel-erograms with harmonic wavelets[J]. Computers and Structures, 2014, 147(10): 26-35. [9] ECHEVERRIA C, RODRIGUEZ E, AGUILAR-CORNEJO M, et al. Linear combination of power-law functions for detecting multiscaling using detrended fluctuation analysis[J]. Physica A: Statistical Mechanics and its Applications, 2016, 460(15): 283-293. [10] 何文平,吴琼,成海英,等.不同滤波方法在去趋势波动分析中去噪的应用比较[J]. 物理学报,2011, 60(2): 45-53. HE Wenping, WU Qiong, CHENG Haiying, et al. Comparison of applications of different filter methods for de-noising detrended fluctuation analysis[J]. Acta Phys. Sin., 2011, 60(2): 45-53. [11] 李力,彭中笑,彭书志,等.去趋势波动分析在齿轮故障诊断中的应用研究[J].中国机械工程,2009, 20(19): 2311-2314. LI Li, PENG Zhongxiao, PENG Shuzhi. Detrended fluctuation analysis for gear fault diagnosis[J]. China Mechanical Engineering, 2009, 20(19): 2311-2314. [12] LIM J H, KHANG E J, LEE T H, et al. Detrended fluctuation analysis and Kolmogorov-Sinai entropy of electroencephalogram signals[J]. Physics Letters A, 2013, 377(38): 2542-2545. [13] 黄朝明,于洪亮,关德林,等. 摩擦振动时频图像特征提取[J]. 振动与冲击,2012, 31(7): 45-49. HUANG Chaoming, YU Hongliang, GUAN Delin, et al. Feature extraction of frictional vibration based on time-frequency image[J]. Journal of Vibration and Shock, 2012, 31(7): 45-49. [14] 孙迪,李国宾,魏海军,等. 磨合磨损过程中摩擦振动变化规律研究[J]. 哈尔滨工程大学学报,2015,36(2): 166-170. SUN Di, LI Guobin, WEI Haijun, et al. Study on variation rules of friction vibration in the process of friction and wear[J]. Journal of Harbin Engineering University, 2015, 36(2):166-170. [15] SUN Di, LI Guobin, WEI Haijun, et al. Experimental study on the chaotic attractor evolvement of the friction vibration in a running-in process[J]. Tribology International, 2015, 88(3): 290-297. [16] 李精明,魏海军,魏立队,等. 摩擦振动信号的经验模式分解和多重分形研究[J]. 振动与冲击,2016, 35(3): 198-203. LI Jingming, WEI Haijun, WEI Lidui, et al. Empirical mode decomposition and multifractal of frictional vibration signal[J]. Journal of Vibration and Shock, 2016, 35(3): 198-203. [17] 吴建军,徐尚义,孙会君. 混合交通流时间序列的去趋势波动分析[J].物理学报,2011, 60(1):78-85. WU Jianjun, XU Shangyi, SUN Huijun. Detrended fluctuation analysis of time series in mixed traffic flow[J]. Acta Phys. Sin., 2011, 60(1): 78-85. [18] KANTELHARDT J W, ZSCHIEGNER S A, KOSCIELN Y, et al. Multifractal detrended fluctuation analysis of nonstationary time series[J]. Physical A, 2002, 316(2): 87-114. Frictional vibration signals based on harmonic wavelet and detrended fluctuation analysis LI Jingming1,2, WEI Haijun1, WEI Lidui1, YANG Zhiyuan1, LIU Chong1, LIU Hong1 (1. Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China;2. Marine Engineering College, Dalian Maritime University, Dalian 116026, China) For the purpose of de-noising and characteristic-extracting of frictional vibration signals,the friction and wear tests of friction pairs were conducted on a reciprocating pin-on-disc tester. The nonlinear and non-stationary frictional vibration signals were decomposed with the harmonic wavelet to realize their de-noising. Then the frictional vibration signals were analyzed with the detrended fluctuation analysis (DFA) to get Hurst exponents under different orders and judge the attribute of data series and their trend enhancement level. The results showed that with friction and wear tests going on, the scaling exponents of the frictional vibration signals reveal a gradual increase trend; the characteristics of the frictional vibration signals can be extracted with the detrended fluctuation analysis; the changing of the scaling exponents of the frictional vibration signals can be used to monitor and identify friction and wear states of friction pairs. harmonic wavelet; detrended fluctuation analysis; scaling exponent; frictional vibration 国家高技术研究发展计划(863计划)(2013AA040203) 2016-01-29 修改稿收到日期:2016-06-12 李精明 男,博士生,讲师,1981年5月生 魏海军 男,博士,教授,博士生导师,1971年7月生 TH117.2 A 10.13465/j.cnki.jvs.2017.15.0352 实验部分

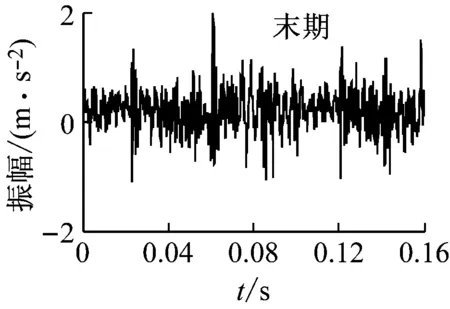
3 试验数据分析
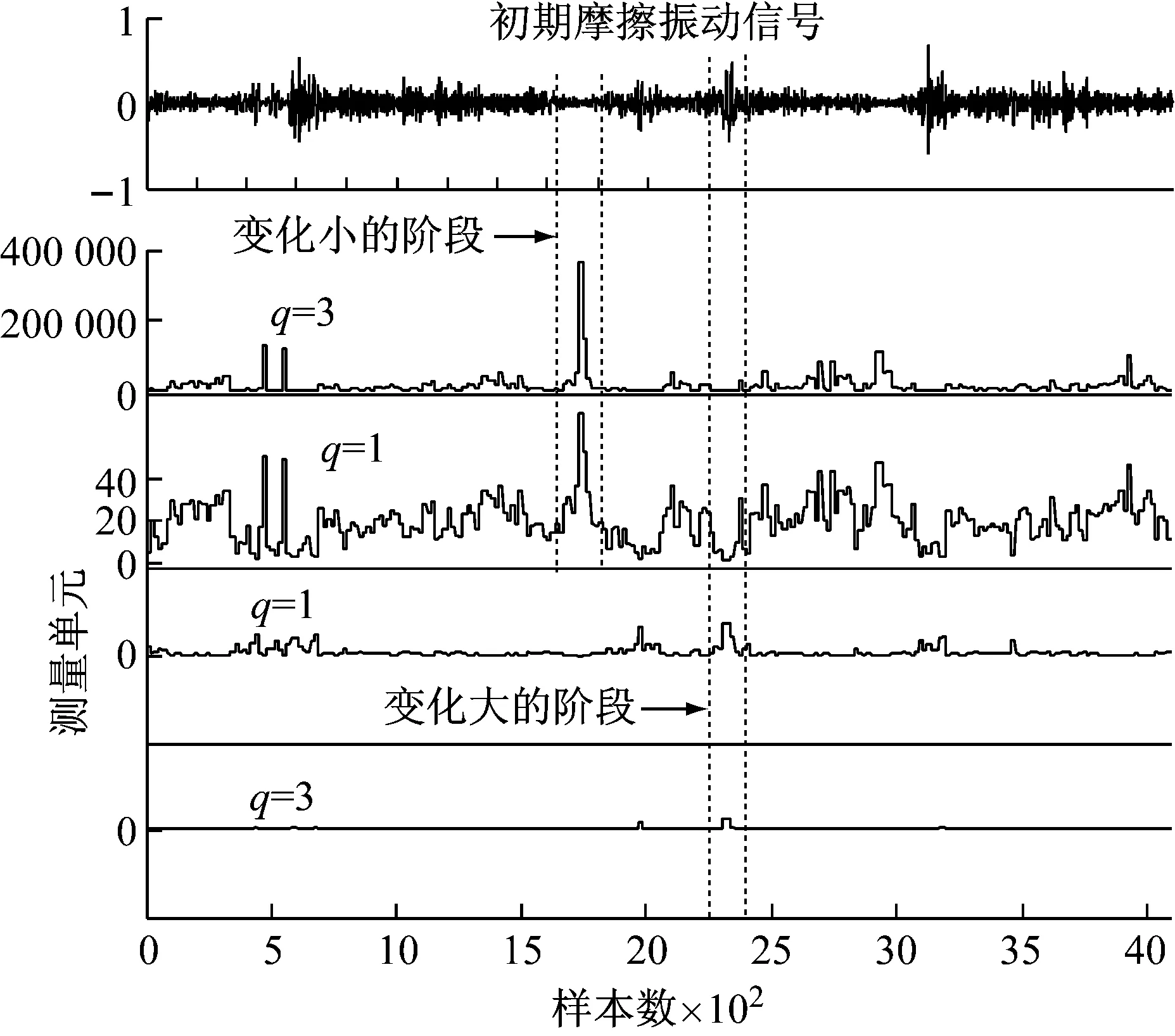

4 结 论
