基于混合人工蜂群和人工鱼群优化的LSSVM脉动风速预测

张永康， 李春祥， 郑晓芬， 徐化喜

(1. 上海大学 土木工程系， 上海 200072； 2. 同济大学 建筑工程系， 上海 200092；3. 上海飞虹钢结构工程有限公司， 上海 200090)

基于混合人工蜂群和人工鱼群优化的LSSVM脉动风速预测

张永康1， 李春祥1， 郑晓芬2， 徐化喜3

(1. 上海大学 土木工程系， 上海 200072； 2. 同济大学 建筑工程系， 上海 200092；3. 上海飞虹钢结构工程有限公司， 上海 200090)

考虑人工蜂群(ABC)和人工鱼群(AFS)算法的各自优势，提出混合智能算法(ABC+AFS)优化选择最小二乘支持向量机(LSSVM)参数的方法，以提高其脉动风速预测模型的性能。AFS算法有较强的全局寻优能力，混合智能算法以AFS算法中的人工鱼寻优方式代替ABC算法中的引领蜂寻优方式，克服ABC算法易陷入局部最优的问题。同时，ABC算法中的正负反馈机制可以克服AFS算法的后期盲目寻优、收敛速度下降的问题。运用基于混合ABC、AFS优化的LSSVM对脉动风速进行了预测，并与基于ABC、AFS和粒子群(PSO)算法优化的LSSVM脉动风速预测结果进行了比较。数值结果表明，基于混合ABC+AFS优化的LSSVM脉动风速预测模型有更好性能，具有工程应用前景。

人工蜂群算法； 人工鱼群算法； 混合智能优化； 最小二乘支持向量机； 脉动风速； 预测性能

在台风作用下，大跨桥梁和高柔结构(例如：超高层建筑)会产生剧烈的抖振。为确保大跨桥梁和超高层建筑的正常运行以及在极端风事件下的安全，现在基本上都在这些结构上安装结构健康监测(SHM)系统来是实时监测台风风速风向和结构的动力响应。尽管如此，布置用于实测此类工程风速风向的风速仪是相当少的，绝大多数位置处的风速需根据少数点的实测记录来进行条件模拟或预测获得，以建立全尺度的实测风荷载信息。因此，发展先进的工程结构风速预测方法至关重要。

预测工程结构的脉动风速时程主要有持续预测法、支持向量机、时间序列法、人工神经网络等方法[1]。其中的基于最小二乘支持向量机(Least Square Support Sector Machine，LSSVM)脉动风速预测模型最近有较大的发展[2-5]。但参数选择直接影响LSSVM的预测性能。为减小参数选择对LSSVM预测性能的影响，学者提出了使用粒子群优化(Particle Swarm Optimization，PSO)[6]、人工鱼群(Artificial Fish Swarm, AFS)算法[7]和人工蜂群(Artificial Bee Colony, ABC)算法[8]等来优化LSSVM的参数。

然而，在上述智能算法中，PSO收敛速度快、参数设置少、实现简单，但易于过早收敛，搜索精度较低；AFS算法对初值和参数选择不敏感、鲁棒性强、能克服局部极值，但后期搜索的盲目性较大，寻优精度较低；ABC算法具有正负反馈机制、参数设置简单、协作能力强，但易于陷入局部最优。本文考虑到ABC和AFS算法的各自优势，提出混合智能算法(ABC+AFS)来优化LSSVM的参数。在ABC算法中，引领蜂在邻域搜索后，跟随蜂在邻域搜索。但两者邻域搜索没有本质差别，属重复工作，是ABC算法易陷入局部最优的根本原因。提出的混合智能算法(ABC+AFS)，以AFS中的人工鱼寻优方式代替ABC中的引领蜂寻优方式，能在可行解范围内全局搜索，增加了ABC种群的多样性，克服了ABC易于陷入局部最优的问题。而且，ABC的正负反馈机制可以克服AFS的后期寻优盲目性。

另一方面，现场实测风速数据是验证预测算法的最直接资料。然而，实测风速数据耗时、耗力，且易受天气和地形条件等因素的影响，还常常出现测出的数据不能用问题。因此，本文运用ARMA模型数值模拟出研究所需的脉动风速时程样本数据库来代替实测风速数据库，并把模拟的脉动风速时程样本数据库划分为训练集和测试集。对训练集学习训练，而对测试集进行预测。根据测试集的预测值与测试集值的平均绝对误差、均方根误差以及相关系数，评价基于混合人工蜂群和人工鱼群优化LSSVM的脉动风速预测性能，以验证基于混合ABC和AFS优化LSSVM的高预测性能。

1 最小二乘支持向量机

最小二乘支持向量机(LSSVM)是在支持向量机(SVM)的基础上，采用误差的二次平方项代替SVM中的不敏感损失函数，将不等式约束改成等式约束，把二次规划问题转化为求解线性方程组问题，以提高求解速度和收敛精度，并成功地应用于函数逼近、分类以及时间序列预测等方面。LSSVM原理如下：

f(x)=ωTφ(x)+b

(1)

根据结构风险最小化原理,此线性回归问题可表示为一个等式约束优化问题。LSSVM目标函数为：

(2)

s.t.yi=ωTφ(xi)+b+ei(i=1,2,…,n)

(3)

式中:J为损失函数;γ为正则化参数且γ>0,ei为误差变量。

将约束优化问题转化为无约束优化问题的拉格朗日等式为：

(4)

将L分别对ω,b,ei,αi求偏导数，并令等于0得方程：

(5)

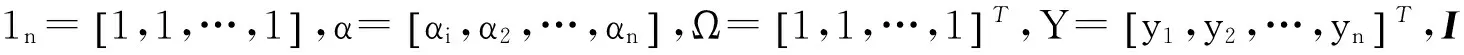
(6)

由式(6)求出α和b, 得到LSSVM回归模型：

(7)

2 人工蜂群和人工鱼群算法

2.1 人工蜂群(ABC)算法

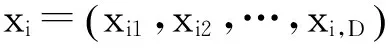
(8)

(9)

依据选择概率大小，跟随蜂选择引领蜂跟随。选择概率越大，引领蜂被选中的概率越大，可表示为：

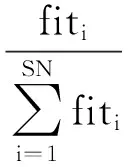
(10)

在ABC算法中，Limit是一个重要的控制参数。若某一个解xi被更新的次数达到Limit时，表明这个解陷入了局部最优。此时，需要放弃该食物源，把该食物源所对应的引领蜂变成侦察蜂，并根据式(11)随机产生一个新解代替xi：

xi=xmin+φij(xmax-xmin)

(11)

式中：xmax,xmin是待优化参数的最大、最小值。

2.2 人工鱼群(AFS)算法

(12)

(1) 觅食行为：设人工鱼的当前状态为Xi，在其感知范围内随机选择一个状态Xj。若Xj的状态优于Xi，则根据式(13)向Xj的方向前进一步；否则重新随机选择状态Xj。若尝试try_number次后，仍然不满足前进条件，则根据式(14)随机移动一步。

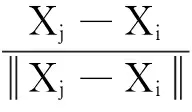
(13)

Xi,next=Xi+rand()·step

(14)

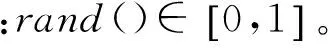
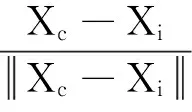
(15)

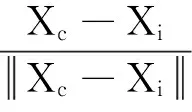
(16)

(4) 随机行为：设人工鱼的当前状态为Xi，在视野中随机选择一个状态。随机行为是觅食行为的一个缺省行为，即：

Xi,next=Xi+rand()·step

(17)

在标准的人工鱼群算法中，公告板是用来记录当前迭代次数下的最优解，并在每次迭代结束后，每条人工鱼(可行解)将自身状态与公告板进行比较，若优于公告板，则更新公告板。在觅食行为中，人工鱼随机选择一个状态，若该状态优于当前状态，则向该方向前进一步，这种方式导致算法收敛过慢；而在聚群和追尾行为中，如果前进条件不满足，则要重新执行觅食行为，导致算法计算量大，运行时间长。为加快AFS算法收敛以及运行速度，王联国等[9]提出了一种简化的人工鱼群算法。在觅食行为中，人工鱼直接移动到在感知范围内能找到的最优位置以加快算法收敛。在聚群和追尾行为中，分别用整个鱼群的中心位置代替邻域中心位置以及用鱼群最优代替邻域最优，避免了对邻域极值以及当前鱼与所有邻域个体鱼之间距离的计算，降低了算法的运行时间。

3 基于ABC+AFS优化LSSVM的脉动风速预测

3.1 基于ABC+AFS优化LSSVM算法

混合ABC和AFS(ABC+ AFS)算法的基本思路简述为：在ABC算法中，引领蜂和跟随蜂皆根据式(8)进行邻域搜索，两者的行为无本质差别，这样会导致人工蜂群开采能力的下降，使算法易于陷入局部最优。以AFS算法中人工鱼代替ABC算法中引领蜂的作用将增加ABC算法种群的多样性，可以克服ABC算法易于陷入局部最优的问题。同时，在ABC算法中，引领蜂、跟随蜂和侦察蜂在群体协作过程中有正、负反馈机制，能克服AFS算法收敛速度慢、算法后期寻优盲目而致使精度下降的问题。

图1给出了基于ABC+AFS优化的LSSVM脉动风速预测流程图，具体阐述如下：

步骤1 设置ABC+AFS算法中人工鱼数量NAF、跟随蜂数量NC、人工蜂群阈值Limit、人工鱼群感知范围初始值以及最小值Visual和Visualmin、步长初始值以及步长最小值Step和Stepmin、人工鱼群拥挤度δ、最大重复尝试次数try_number以及算法最大迭代次数MCN。确定LSSVM参数σ和γ的范围，随机生成N个食物源(初始解)，且N=NAF=NC。表1给出了ABC+AFS算法的参数初始值以及LSSVM参数的范围。

表1 ABC+AFS算法的参数初始值以及LSSVM参数的范围

步骤2 基于ARMA模拟脉动风速时程样本，划分为训练集和测试集，并根据式(18)进行归一化处理；

(18)

式中：xmin和xmax分别为输入的最大值最小值。

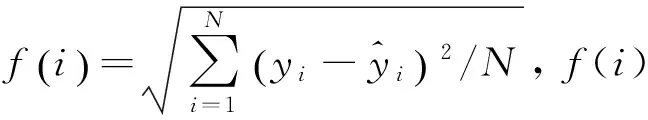
步骤4 以人工鱼代替引领蜂在可行解的范围内进行觅食行为，并根据简化的人工鱼群模型更新自己的位置。计算每个人工鱼适应度，并与公告板中最优值比较，更新公告板信息。

步骤5 跟随蜂依据式(10)计算选择概率以选择食物源，并根据式(8)进行邻域搜索，再根据贪婪原则更新食物源。计算食物源的适应度，更新公告板。

步骤6 判断是否有食物源未被更新的次数达到了阈值Limit。若达到阈值，则放弃该食物源，并将与该食物源对应的跟随蜂转换为侦察蜂，根据式(11)产生新的食物源；否则，转到步骤7。

步骤7 判断是否达到最大迭代次数MCN(本文MCN=200，依据如图2所示)。若达到MCN，输出公告板记录的最优解，算法结束；否则，转步骤4。

3.2 数值比较验证

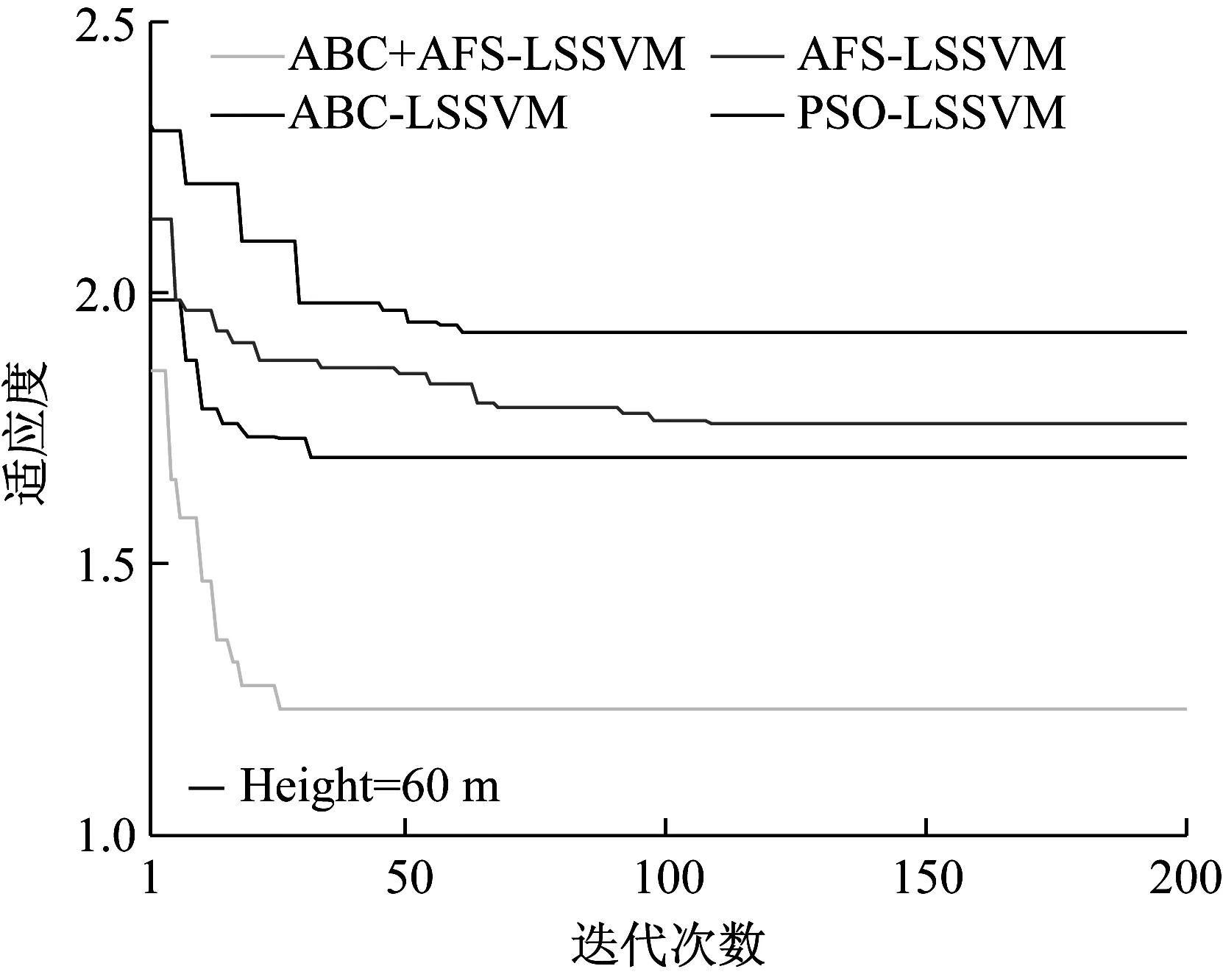
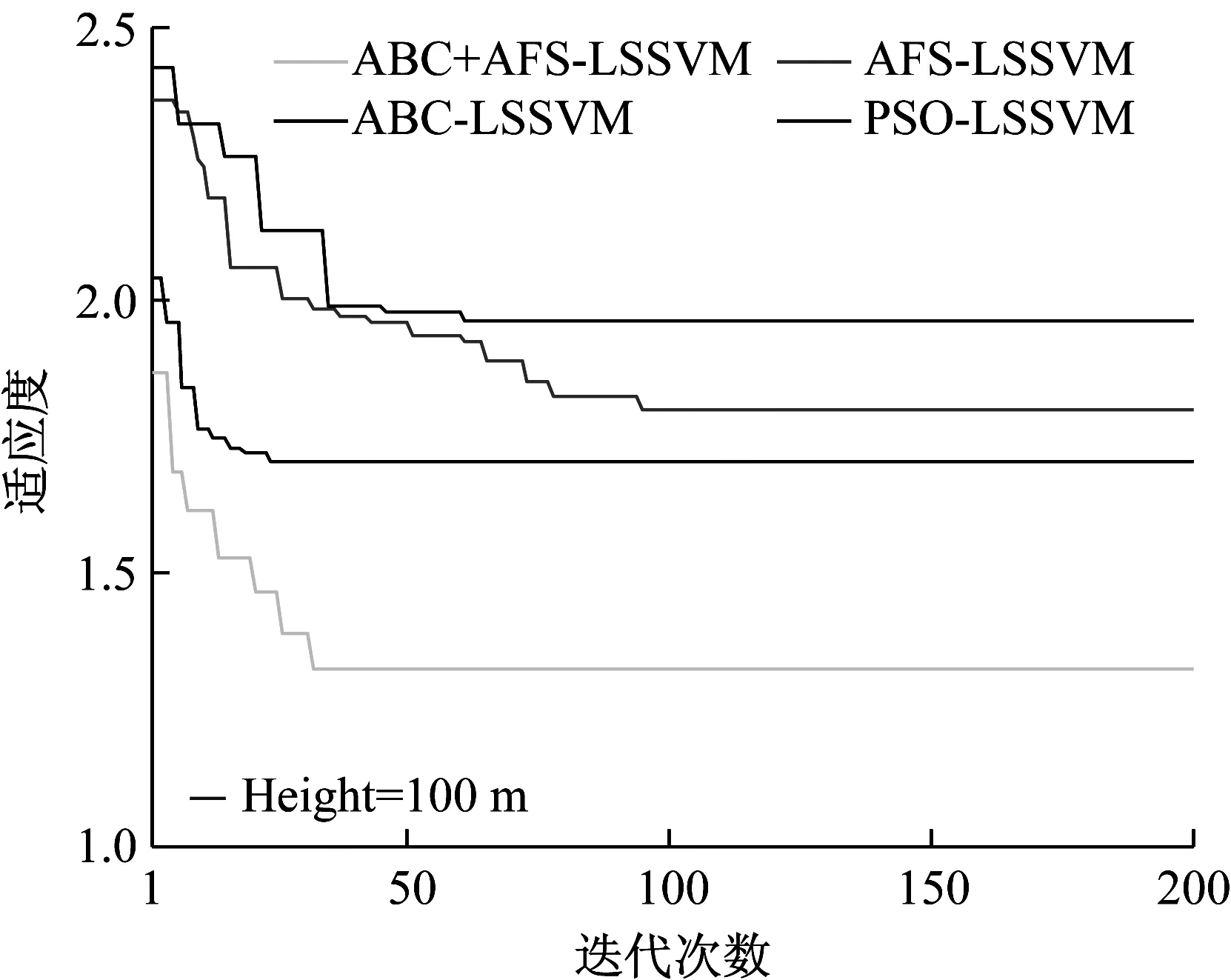
图2 迭代次数和适应度值的关系

表2 数值模拟参数

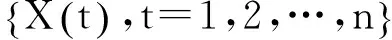
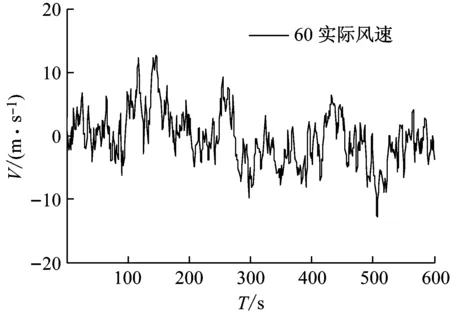
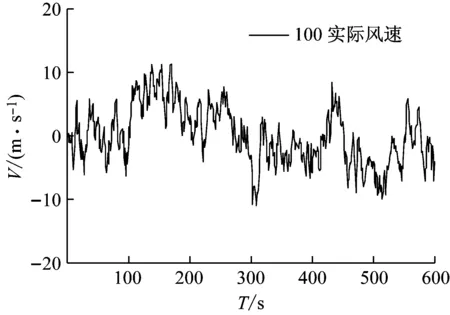
图3 60 m和100 m处模拟脉动风速时程

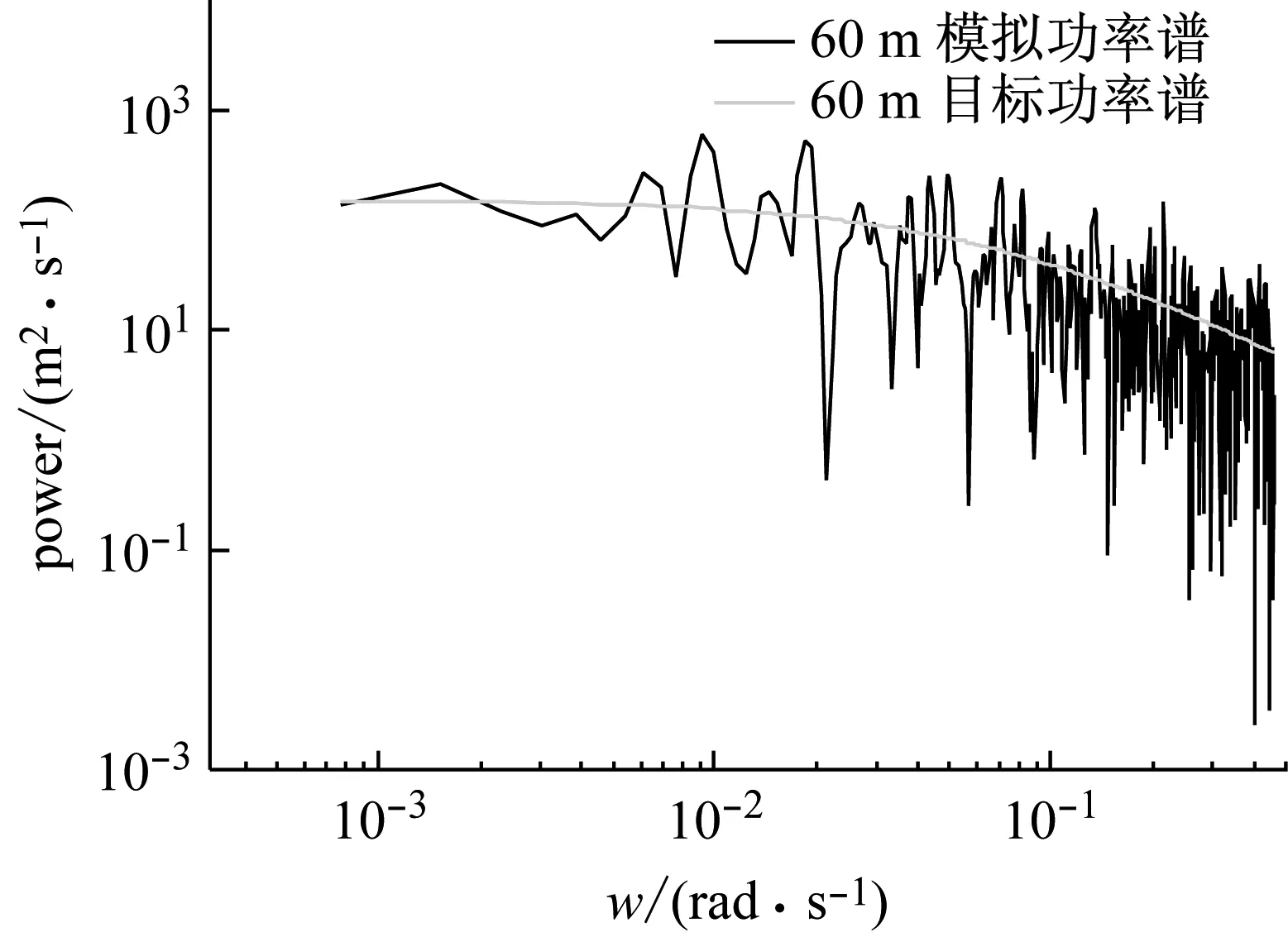
图4 60 m和100 m模拟值和目标值功率谱的对比图

由图4可看出，在60 m和100 m处，脉动风速的模拟功率谱与目标功率谱基本吻合。图5表明，自相关函数的模拟值和目标值也能很好地吻合；在延迟时间为零时，相关性达到最大，表明原始脉动风速样本的可靠性。现分别取60 m和100 m高度处的前500 s风速数据为训练集，后100 s为测试集，嵌入维数m=10，建立基于ABC+AFS优化LSSVM的脉动风预测模型，以对测试集进行预测。为了比较，分别给出了基于ABC、AFS和PSO优化LSSVM的脉动风速预测结果。图6为基于ABC+AFS、ABC、AFS和PSO优化LSSVM的预测风速幅值与实际风速幅值对比。图7为基于ABC+AFS、ABC、AFS和PSO优化LSSVM的预测风速与实际风速自相关函数对比。

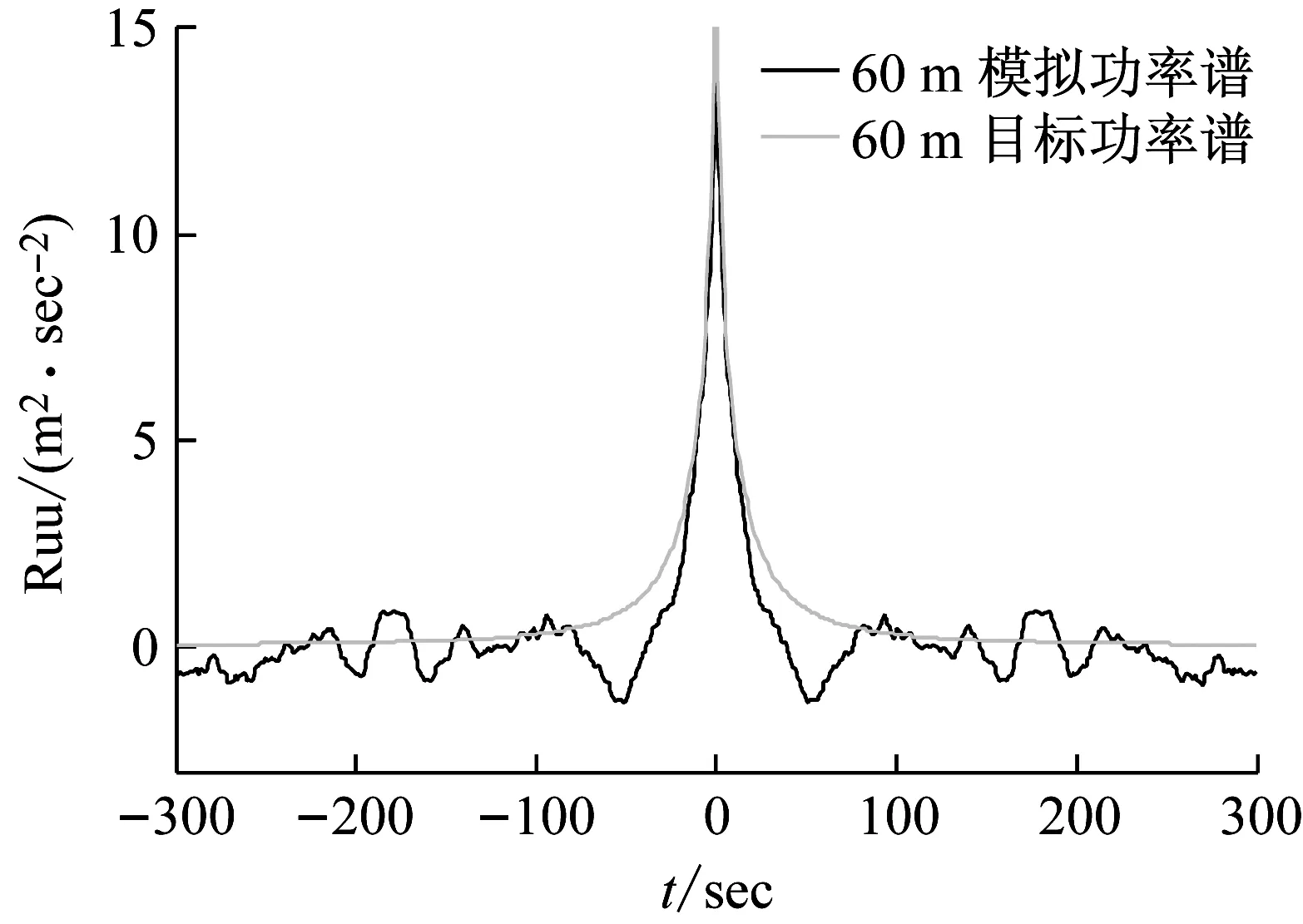
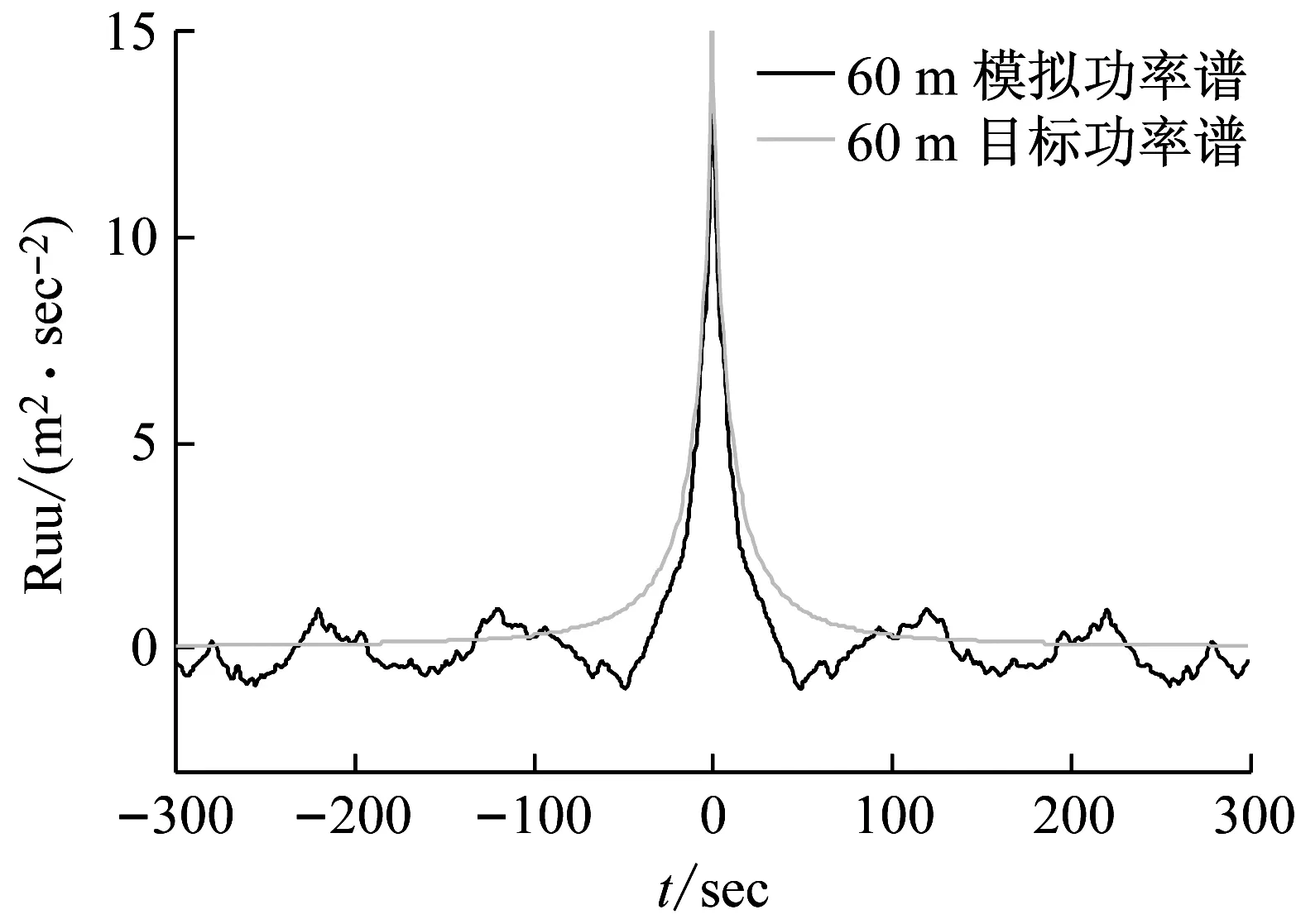
图5 模拟值和目标值自相关函数的对比图

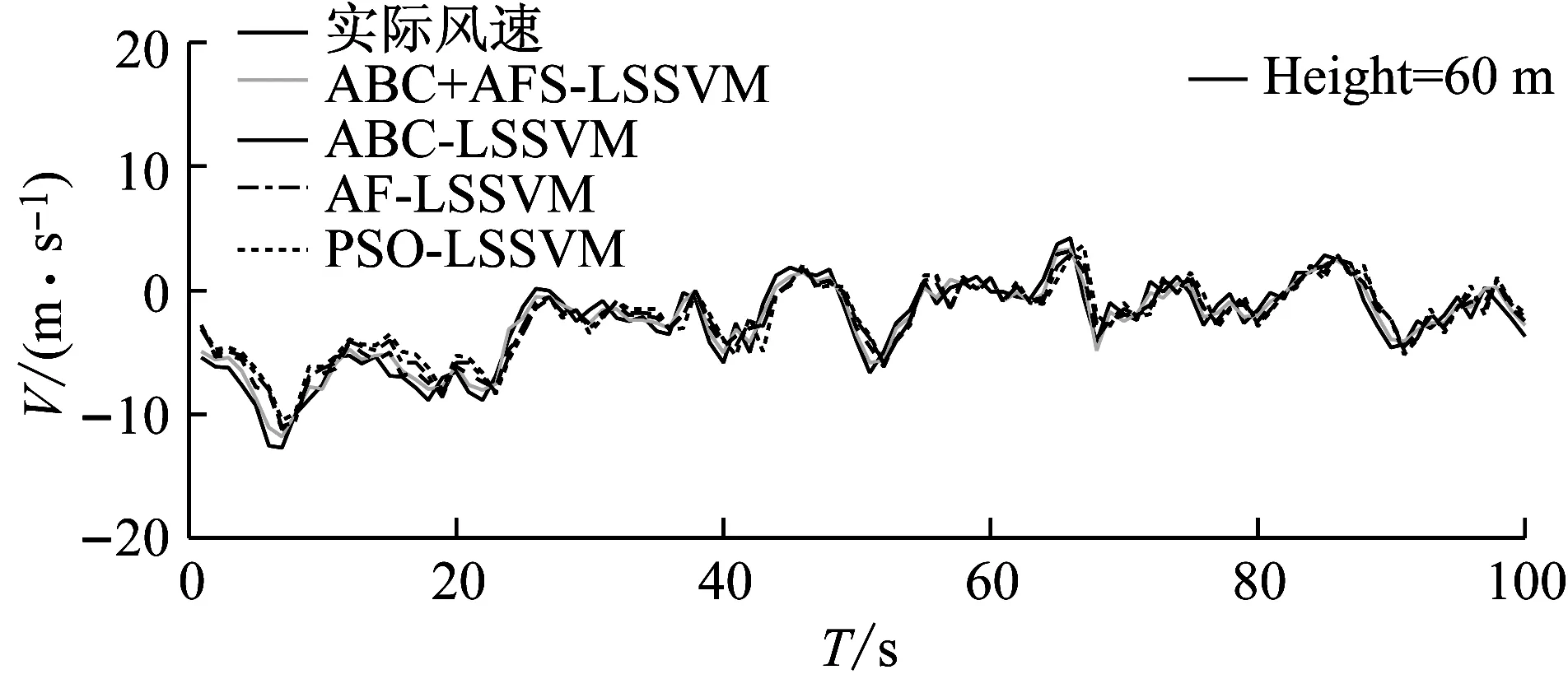
图6 在60 m和100 m处, 预测风速与实际风速的幅值对比

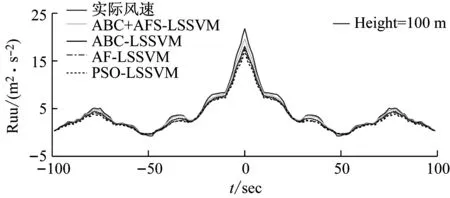
图7 在60 m和100 m处，预测风速与实际风速自相关函数的对比

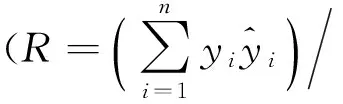
从表3和表4可看出，在预测精度方面，在60 m和100 m高度处ABC+AFS-LSSVM模型对脉动风速预测值与实际值的平均绝对误差(MAE)以及均方根误差(RMSE)最小，且较PSO-LSSVM、AFS-LSSVM和ABC-LSSVM模型的预测精度有明显的提高。在相关性方面，ABC+AFS-LSSVM模型在60 m和100 m高度处脉动风速预测值与实际值的相关系数值(R)均大于0.9(相关系数R>0.8表示相关性较强)，表明预测值与实际值具有很强相关性。在训练时间方面，PSO-LSSVM、ABC-LSSVM模型耗时短，但预测精度不高；ABC+AFS-LSSVM模型耗时较AFS-LSSVM模型有较大的改善，且能保证预测精度。

表3 测试集性能指标

表4 ABC+AFS-LSSVM预测模型测试集性能指标提高的百分比

Tab.4 Increased percentage of prediction performance index of ABC+AFS algorithm based LSSVM for testing data set

预测模型ABC+AFS-LSSVMMAERMSERMAERMSERPSO-LSSVM41%36%13%40%33%14%AFS-LSSVM34%30%11%26%22%8%ABC-LSSVM30%27%8%22%20%6%60m100m

4 结 论

提出一种基于混合ABC+AFS优化LSSVM的脉动风速预测算法。混合优化结合ABC和AFS两种智能优化算法的优势，克服了ABC算法易于陷入局部最优以及AFS算法训练时间长、收敛速度慢的问题。数值结果表明，ABC+AFS-LSSVM的脉动风速预测模型在MAE、RMSE、R三个性能指标方面均优于ABC-LSSVM、AFS-LSSVM和PSO-LSSVM模型；在训练时间和收敛速度上，ABC+AFS-LSSVM模型比AFS-LSSVM模型有较大的改善。因此，基于混合ABC+AFS优化LSSVM的脉动风速预测算法可应用于实际脉动风速预测，可根据历史脉动风速数据预测未知的脉动风速，为结构抗风设计提供完整的脉动风速时程。

[1] MONFARED M, RASTEGAR H, KOJABADI H M. A new strategy for wind speed forecasting using artificial intellingent methods[J]. Renewable Energy, 2002, 27(2):163-174.

[2] SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing, 1999, 9(3): 293-300.

[3] YING D U, LU J P, LI Q. Short-term wind speed forecasting of wind farm based on least square-support vector machine[J]. Power System Technology, 2008, 32(15):62-66.

[4] 李春祥, 迟恩楠. 基于优化组合核和Morlet小波核的LSSVM脉动风速预测方法[J]. 振动与冲击, 2016,35(18):52-57.

LI Chunxiang, CHI Ennan. Forecasting fluctuating wind velocity using optimized combination kernel and Morlet wavelet kernel based LSSVM[J]. Journal of Vibration and Shock, 2016,35(18):52-57.

[5] 李春祥, 迟恩楠, 何亮, 等. 基于时变ARMA和EMD-PSO-LSSVM算法的非平稳下击暴流风速预测[J]. 振动与冲击, 2016，35(17)：33-38.

LI Chunxiang, CHI Ennan, HE Liang, et al. Prediction of nonstationary downburst wind velocity based on time-varying ARMA and EMD-PSO-LSSVM algorithms[J]. Journal of Vibration and Shock, 2016,35(17):33-38.

[6] 张弦, 王宏力. 基于粒子群优化的最小二乘支持向量机在时间序列预测中的应用[J].中国机械工程, 2011, 22(21): 2572-2576.

ZHANG Xian, WANG Hongli. The application of least squares support vector machine based on Particle Swarm Optimization in the forecasting of time series[J]. China Mechanical Engineering, 2011, 22(21): 2572-2576.

[7] NESHAT M, SEPIDNAM G, SARGOLZAEI M, et al. Artificial fish swarm algorithm:a survey of the state-of-the-art, hybridization, combinatorial and indicative applications[J]. Artificial Intelligence Review, 2014, 42: 965-997.

[8] KARABOGA D, AKAY B. A comparative studay of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(14): 108-132.

[9] 王联国,洪毅,赵付清,等.一种简化的人工鱼群算法[J]. 小型微型计算机系统, 2009, 30(8): 1663-1667.

WANG Lianguo, HONG Yi, ZHAO Fuqing, et al.Simplified artificial fish swarm algorithm[J]. Journal of Chinese Computer Systems, 2009, 30(8): 1663-1667.

Fluctuating wind velocity prediction using LSSVM based on hybrid intelligent optimization of ABC and ABF

ZHANG Yongkang1， LI Chunxiang1， ZHENG Xiaofen2， XU Huaxi3

(1. Department of Civil Engineering, Shanghai University, Shanghai 200072, China；2. Department of Structural Engineering, Tongji University, Shanghai 200092, China；3. Shanghai Feihong Steel Structure Engineering Co. Ltd.，Shanghai 200090, China)

Considering advantages of the artificial bee colony(ABC)and the artificial fish swarm (AFS) algorithms, a hybrid intelligent optimization algorithm called ABC+AFS algorithm was used to optimize parameters of the least square support vector machine (LSSVM) in order to improve its performance of predicting fluctuating wind velocity. Due to AFS algorithm having a better ability of skipping over local optima, the searching optima mode of artificial bees in ABC algorithm was replaced with that of artificial fishes in AFS algorithm to overcome problems of ABC algorithm being easily to fall into local optima. Concurrently, the positive and negative feedback mechanism in ABC algorithm was used to overcome problems of blindly searching optima and convergent speed dropping in the late period of AFS algorithm. LSSVM based on the ABC+AFS algorithm was used to predict fluctuating wind velocity. The results were compared with those using LSSVM based on ABC, AFS, and PSO algorithms, respectively. The numerical results showed that LSSVM based on the ABC+AFS algorithm has a better performance of predicting fluctuating wind velocity and a bright prospect of engineering application.

artificial bee colony (ABC); artificial fish swarm (ABF); hybrid intelligent optimization; least square support vector machine (LSSVM); fluctuating wind velocity; prediction performance

国家自然科学基金(51378304)

2016-03-04 修改稿收到日期：2016-08-22

张永康 男，硕士生，1990年10月生

郑晓芳 女，博士，1963年1月生

TU311

A

10.13465/j.cnki.jvs.2017.15.030