基于增广SVM的结构动力学模型修正方法研究
2017-08-30陈国平
陈 喆, 何 欢, 陈国平
(南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016)
基于增广SVM的结构动力学模型修正方法研究
陈 喆, 何 欢, 陈国平
(南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016)
研究了基于代理模型的有限元模型修正方法,针对支持向量机(Support Vector Machine, SVM)在处理非线性程度不高函数时容易出现过拟合,提出了一种采用混合基函数形式的增广SVM方法。该方法首先是在结构动力学试验结果和结构有限元模型计算分析结果的基础上,根据设计要求、灵敏度计算或工程经验选择适合的待修正参数、修正范围来确定修正样本空间,并给出样本点,其次采用增广SVM方法构造每组样本点和与之对应的目标函数之间的代理模型,采用基于Pareto最优解的多目标优化方法,以代理模型输出为目标,样本空间为变量,寻找待修正参数在修正区间内的全局最优解。用代理模型代替原有的有限元模型进行相关的计算分析,避免在模型修正过程中反复调用原有限元模型进行计算带来的高昂计算成本。通过算例一表明,增广SVM的预测结果较传统SVM方法精度更高,而算例二、三则说明所提出的基于增广SVM方法的结构动力学模型修正方法具有实际应用价值,同时计算结果具有很高的精度。
代理模型; 多目标优化; 增广SVM; 模型修正
由于有限元建模过程中会根据建模要求、工程经验和计算规模限制等对结构进行简化,再加上结构几何尺寸、材料特性、以及边界条件等因素的影响,使有限元模型与真实结构之间不可避免的存在误差[1-2],在某些情况下,有限元模型无法满足实际问题的精度要求。为了提高有限元模型计算精度,Rodden等[3]提出了模型修正的观点,利用试验数据对有限元模型进行修正,使修正后的有限元模型拥有更高精度,并且能够更加真实的反映结构的动力学特性[5-6]。本文针对当前主流的基于代理模型的有限元模型修正问题进行讨论。
代理模型的实质是以拟合精度或预测能力为约束,利用近似技术对离散数据进行回归或插值的数学模型,通过有限的已知点响应构造近似函数表达式对未知区域进行预测[7-8]。目前常用构造代理模型的方法有:经典响应面法(Response Surface Method, RSM)[9]、移动最小二乘法(Moving Least Squares, MLS)[10]、人工神经网络[11]、径向核函数法(Radial Basis Function, RBF)[12]、Kriging差值[13-14]以及支持向量机(SVM)[15]等,其中SVM在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势,近年来得到广泛应用。
SVM是基于统计学习理论的通用机器学习方法,其思想源于Vapnik等[16]在1963年提出的用于解决模式识别问题的支持向量方法。Clarke等[17]采用支持向量机作为代理模型,通过典型的工程实例与响应面、径向核函数、多变量回归和Kriging模型的性能进行比较,结果表明支持向量回归机代理模型的准确性和鲁棒性均优于其他四种模型;Ayestaran等[18]采用支持向量回归机完成了阵列天线设计;Yun等[19]利用支持向量回归机模型成功用于结构多目标优化中Pareto解的求取;Saqlain等[20]将支持向量回归机代理模型引入的多学科领域,实现了考虑节流效应时运载火箭的多学科优化;Wang等[20]采用smooth-支持向量机代理模型,实现了结构优化;Qazi等[22]研究了不同样本策略对支持向量回归机性能的影响,提出了一种新的样本策略,实现了运载火箭的优化;Wang等[23]采用最小二乘支持向量机,实现了钣金结构有优化;朱跃等[24-25]针对模型确认中有限元模型的不确定性建模问题,提出了一种基于支持向量回归机的不确定性建模方法;费庆国等[26]提出了一种基于方差分析的参数筛选、基于回归分析的响应面拟合以及利用响应面的模型修正方法,该方法适用于线性、低频情况,且易于推广到非线性、冲击等领域,同时具有计算量小,适合工程应用等特点;张冬冬等[27]结合Kriging理论构造响应面代理模型和有限元模型确认思想,以Garteur benchmark飞机结构瞬态响应分析为例,证明了Kriging响应面能准确对有限元模型响应进行预测;此外,Ren等[28]将基于响应面的模型修正方法运用到以简化模型预测实际结构响应的问题上,结果表明,该方法具有良好的精度和预测效果。
本文将对基于SVM的代理模型在模型修正中的应用展开讨论,并在此基础上提出一种改进的SVM方法。
1 一种改进的SVM方法
1.1 SVM回归基本原理
支持向量机(SVM)方法的基本思想是:定义最优线性超平面,并把寻找最优线性超平面的算法归结为求解一个最优化的问题。进而基于Mercer展开定理,通过非线性映射φ,把样本空间映射到一个高维乃至于无穷维的特征空间,使在特征空间中可以应用线性学习机的方法解决样本空间中的高度非线性分类和回归等问题。简单的说就是实现升维和线性化。
y=f(x)
(1)
可以用来模拟样本输入与输出之间的关系,输入样本如图1所示。
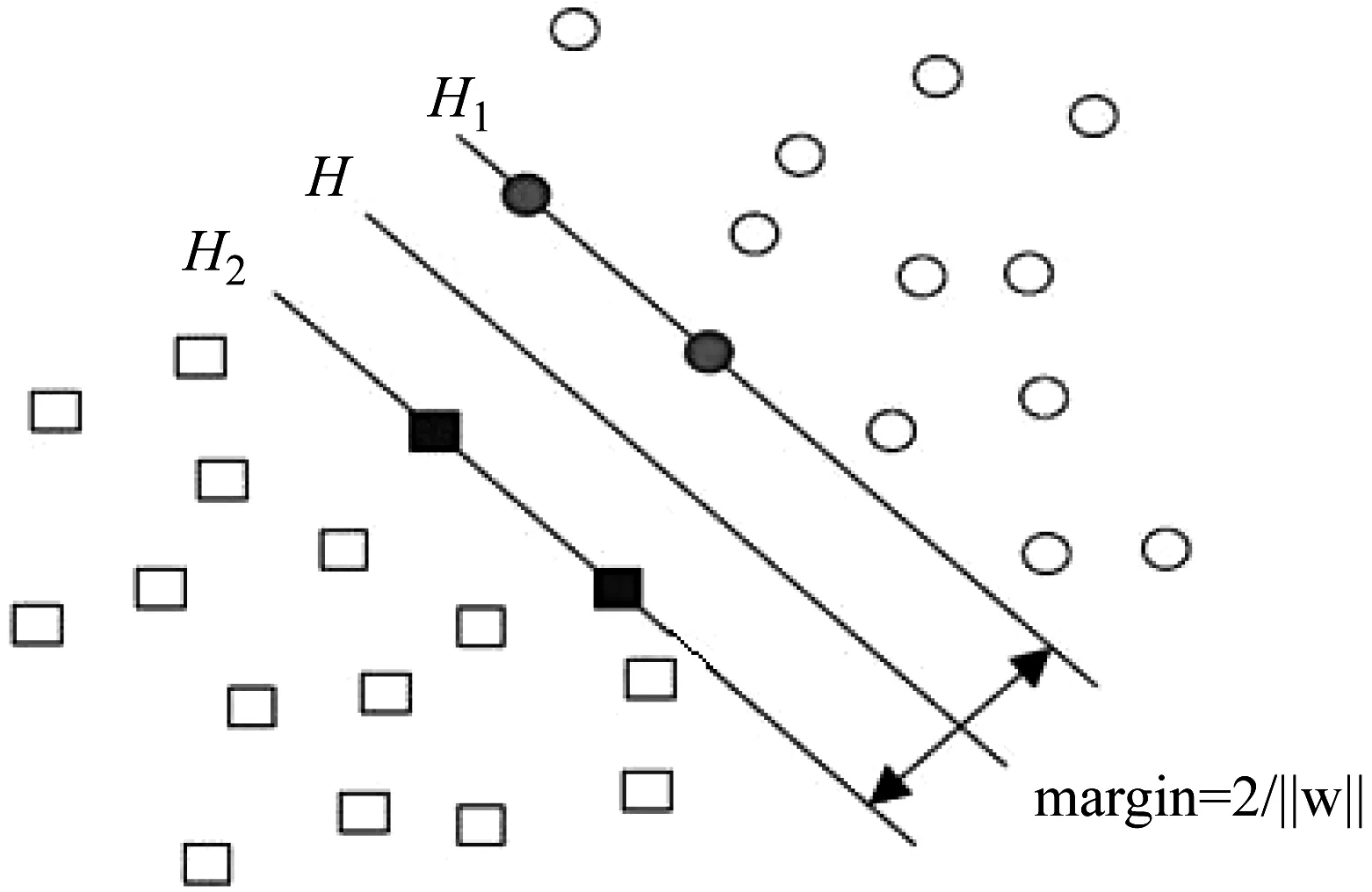
图1 支持向量机线性可分模型
引入ε-不敏感损失函数[29]
(2)
则支持向量机回归问题可以用如下的优化问题表达
(3)
可以通过构造Lagrange函数解决上述的优化问题:
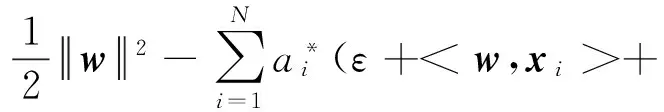
(4)

(5)
式(4)和(5)的求解问题实际上可以转化为一个凸二次优化问题
(6)
(7)

1.2 增广SVM
考虑到允许拟合误差存在的情况,引入松弛变量ξ≥0和ξ*≥0来改善其泛化性能,纳入松弛变量的支持向量回归机的数学模型为:
(8)
式中,C>0为正则化参数,通常称为惩罚因子,用来平衡回归函数的平滑程度和偏差大于ε的样本点个数。
求解上述形式的支持向量机问题一般采用对偶理论,将其转化为二次规划问题。建立Lagrange方程

(9)


(10)
根据KKT条件,在最优解处存在
(11)
和
(12)
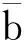
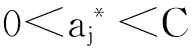
(13)
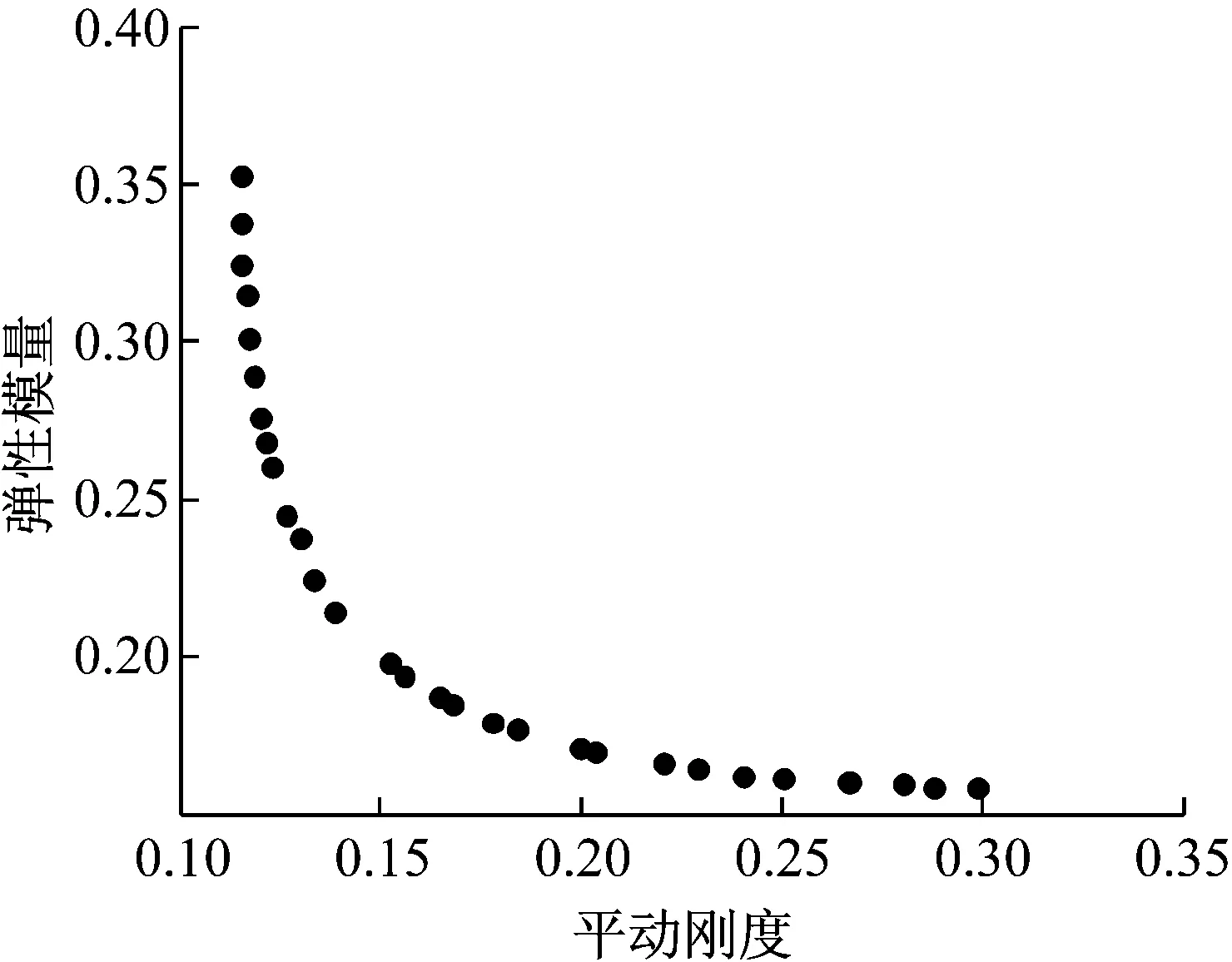
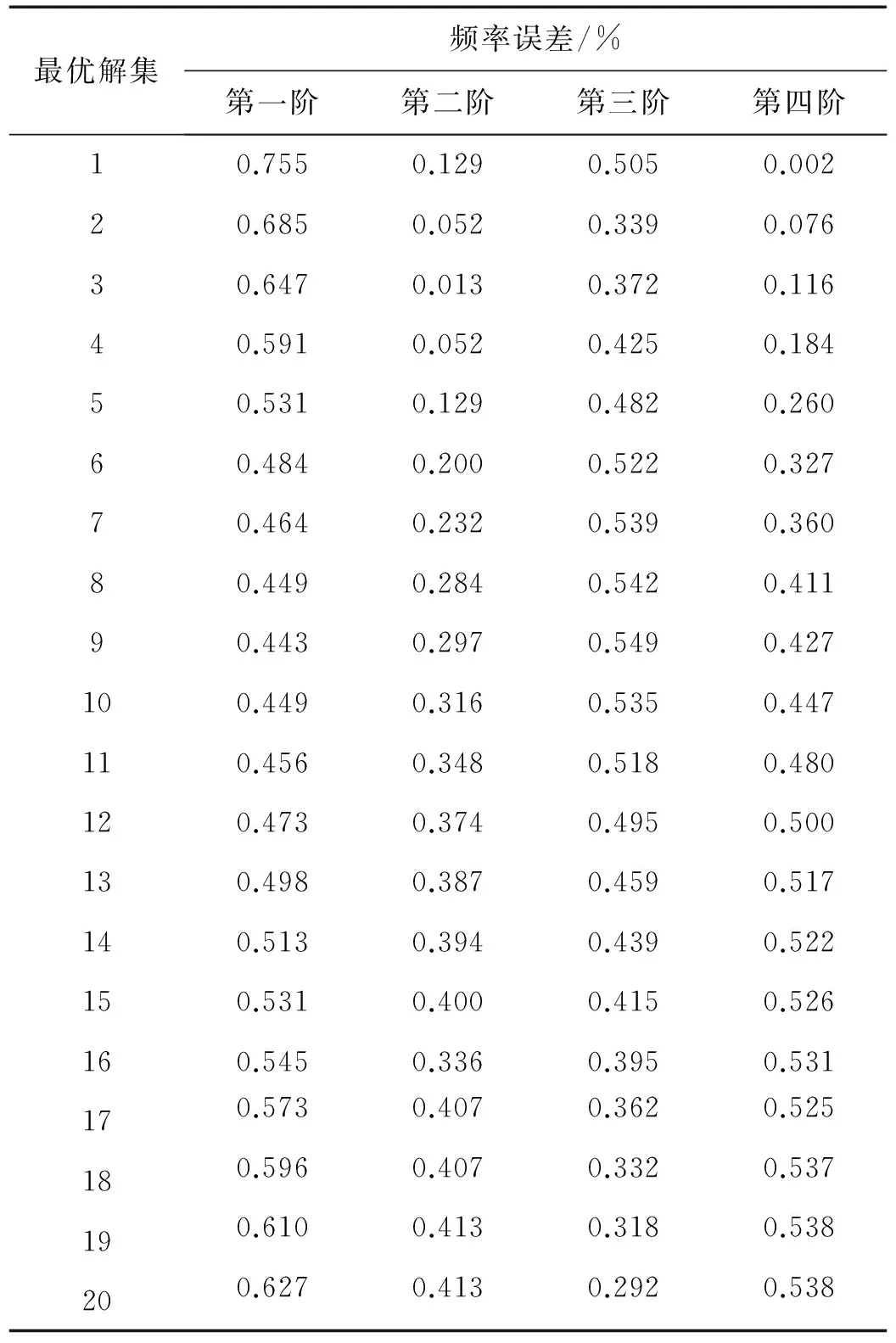
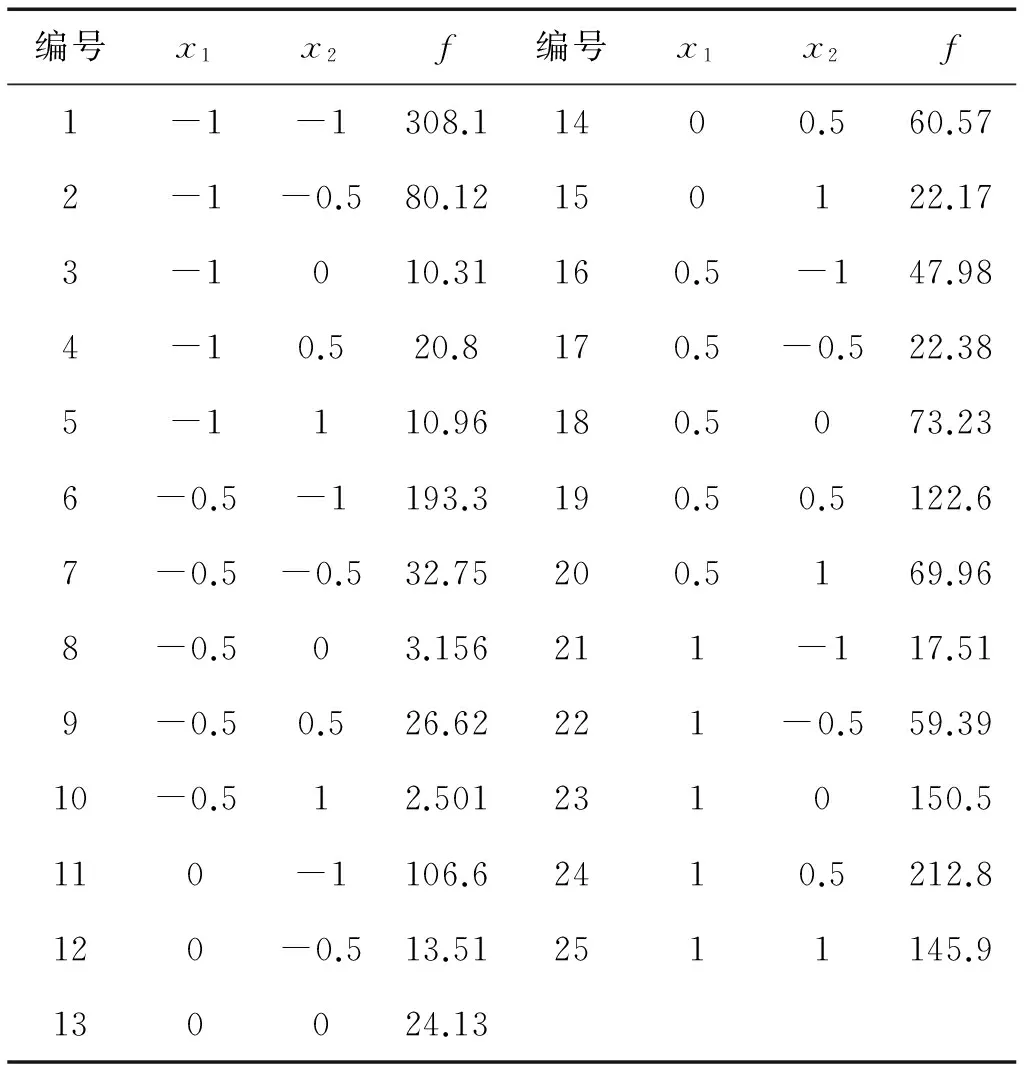
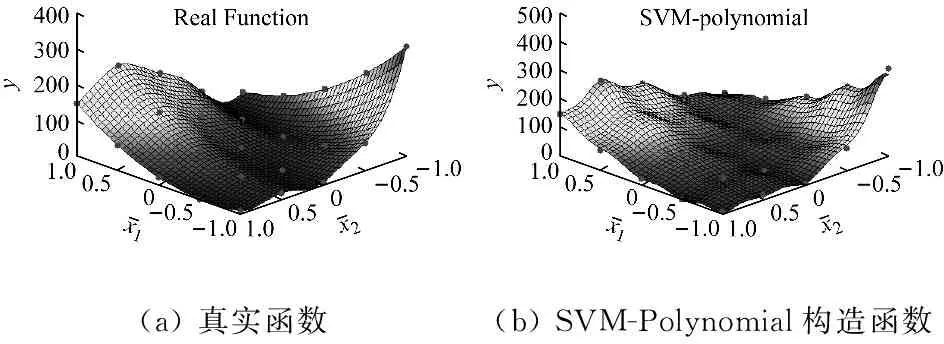
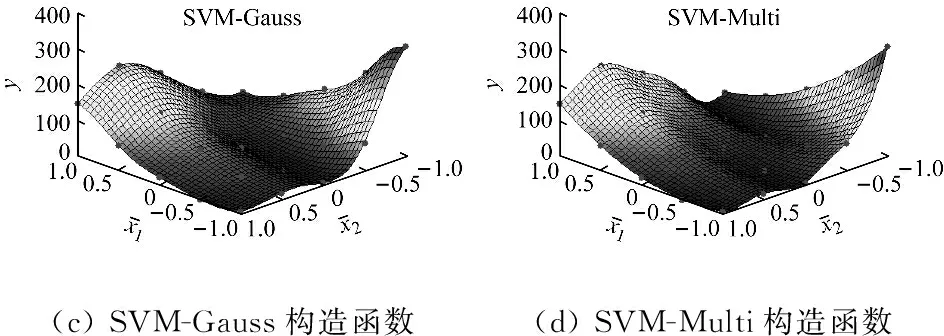
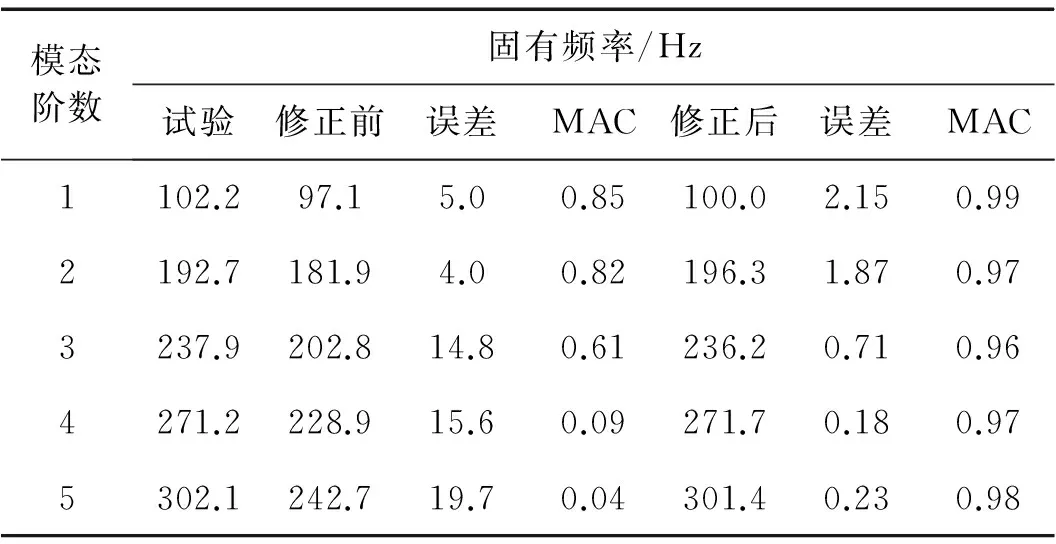
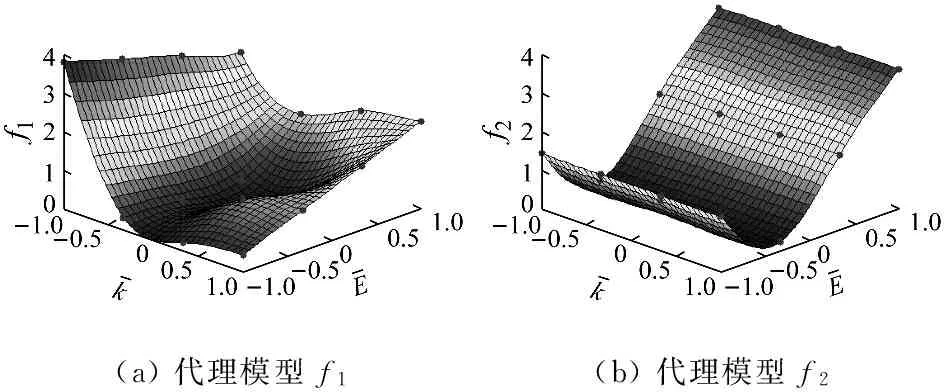
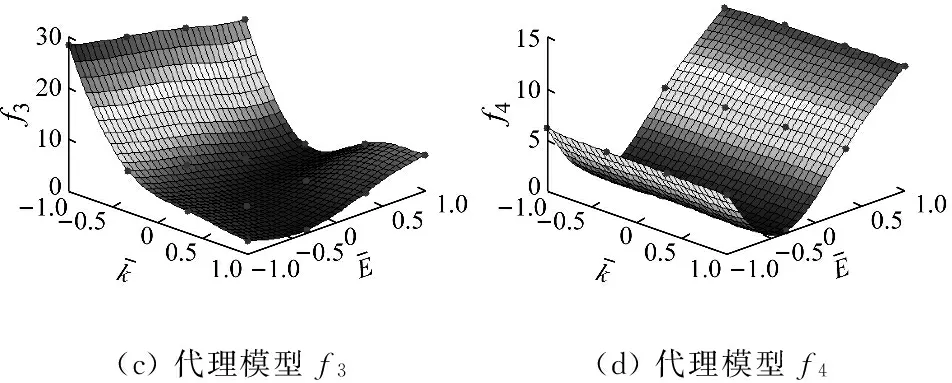
当0 (14) 如果样本是线性不可分的,那么在求解回归问题时会陷入无限循环而导致问题不可解,一般采用的方法是引入非线性映射φ,将原始样本输入空间映射到高维的特征空间,然后在特征空间中进行线性逼近。则式(10)可以改写为 (15) 为了简化回归问题的求解过程,引入核函数(Kernel function),核函数满足 k(x,x′)=<φ(xi),φ(xi)> (16) 则式(15)变为 (17) 式中:k(x,x′)为实对称矩阵,且满足Mercer条件。 (18) 式中,ur=[1,…,1]1×r。 基函数的选取对SVM的泛化能力有很大影响。采用Quad基和Gauss基的SVM适用于构造具有强非线性特征的代理模型问题。若真实函数非线性程度较低,或表现出较为显著的线性特征,考虑到ε的影响,采用这两类基函数的SVM会出现明显的过拟合现象。对于这个问题,采用多项式基函数的SVM会获得更好的拟合效果。由于不同基函数的选取对待拟合函数自身的非线性特征有关,仅仅采用单一的基函数对一般性函数的拟合存在困难。针对这一问题,本文将Gauss基函数或Quad基函数与常规的多项式基函数相混合,采用这种新的混合基函数来对传统SVM进行改进。改进后的SVM模型的增广形式表达式为 (19) 由于待求的参数数目要多余方程数目,因此式(19)无法定解,为此可引入正交性条件: (20) 值得注意的是,增广形式的SVM基函数矩阵是非正定矩阵。而在SVM构造代理模型的过程中采用二次规划求解最优系数时要求核函数矩阵必须是正定矩阵,因此,需要构造适合的响应函数用于二次规划求解问题。 定义新的响应函数表示为: g(x)=(k(x)-f)T(k(x)-f) (21) 式中:k(x)表示核函数,f表示原始响应值。因此,新的二次规划问题描述为: (22) 对于模型修正问题,可以利用增广SVM构造修正目标的代理模型。假设x为修正变量,y为修正目标函数。设修正变量与修正目标函数之间的真实映射关系可表示为: y=f(x) (23) 表达式(14)的反函数为: x=f-1(y) (24) 由于目标函数y可以通过结构动力学模型试验实际之间或者间接得到,将y作为增广SVM的输入,用增广SVM来描述函数关系式f-1,则结构设计参数x将作为增广SVM的输出,从而达到模型修正的目的。 利用增广SVM构造代理模型进行结构动力学模型修正的具体步骤如下: (1) 目标函数的选取。可以根据试验结果或者实际需求选择目标函数,通常可以选择模态频率、频响函数、模态频率残差或者频响函数残差等作为增广SVM的输入。本文以模态频率残差作为目标函数。 (25) 则模型修正问题的目标函数可以表示为: (26) (2) 样本空间的选择。样本点的选取需要采用合理的试验设计方法,试验设计方法实际上就是有关如何合理安排试验的数学方法,它是代理模型的取样策略,决定了构造代理模型所需样本点的个数和样本点的空间分布情况。现阶段常用的试验设计方法包括:全面析因试验设计、中心复合试验设计、正交试验设计、均匀试验设计、随机投点设计和拉丁方方法等。本文主根据设计参数数量的不同,分别采用全面析因试验设计和中心复合试验设计方法构造样本点。 (3) 代理模型精度检验。对代理模型采用R2判定系数和相对均方差(RMSE)检验其精度,其计算式分别为 R2=1-SSE/SST (27) (28) 式中:p为代理模型中非常数项的个数;SSE是误差平方和;SST是总误差平方和。SSE与SST的计算公式分别如下 (29) (30) (4) 结构动力学模型修正。当有限元模型参数和试验模型参数完全一致时,目标函数值在理论上为零。因此,可以通过优化计算,得到修正区间内的最优解,即为修正后的设计参数值。将修正后的设计参数值代入有限元模型进行计算和精度检验,若精度满足要求,则可以通过有限元模型进行后续的计算分析。 模型修正过程的流程图如图2所示。 3.1 两参数数值算例 以一个非线性数学函数——Branin rcos函数来比较由SVM-Quad、SVM-Gauss和SVM-Multi构造的全局近似函数的精度。Branin rcos函数有两个设计变量,形式如下: (31) 定义x1∈[-5,10],x2∈[0,15]。 采用不同的代理模型构造得到的代理模型及真实函数曲面的对比如图3所示,其中SVM-Gauss表示Gauss基SVM,SVM-Polynomial表示多项式基SVM,SVM-Multi表示增广SVM。 图2 基于代理模型的结构动力学模型修正方法流程图 编号x1x2f编号x1x2f1-1-1308.11400.560.572-1-0.580.12150122.173-1010.31160.5-147.984-10.520.8170.5-0.522.385-1110.96180.5073.236-0.5-1193.3190.50.5122.67-0.5-0.532.75200.5169.968-0.503.156211-117.519-0.50.526.62221-0.559.3910-0.512.5012310150.5110-1106.62410.5212.8120-0.513.512511145.9130024.13 对比上图可以明显发现,基于不同基函数的SVM都可以根据样本点对真实函数进行拟合。但不同的是, 基于SVM-Polynomial的构造函数的拟合结果和精度都相对较差,存在严重的过拟合现象。基于SVM-Gauss的构造函数虽然在一定程度上可以比较准确的对真实函数进行描述,但从图3(c)中可以看出,在某些区域,构造函数与真实函数之间仍存在明显偏差。而基于SVM-Multi的构造函数则可以最准确的描述真实函数,精度最高。为了更加直观的说明这一问题,同样采用全面析因试验设计方法构造一系列的检验样本点来检验构造函数的精度,检验样本点如表2所示。 (a)真实函数(b)SVM-Polynomial构造函数 (c)SVM-Gauss构造函数(d)SVM-Multi构造函数 图3 基于不同基函数的构造函数与真实函数对比情况 Fig.3 The contraction between the constructor function and the real function based on different basis function 表2 检验样本点 根据式(27)和(28)计算得到R2和RMSE,如表3所示。 表3 R2和RMSE 从表3中可以明确看出,在SVM-Quad、SVM-Gauss和SVM-Multi三种方法中,SVM-Multi的R2值最大,RMSE值最小,这进一步说明在这三种代理模型构造方法中,增广SVM方法在处理一般函数问题中,其构造函数的精度比传统SVM方法更高,对真实函数的描述更准确。 3.2 某机翼模型结构动力学模型修正 本算例选用某机翼结构为研究对象,机翼有限元模型如图4所示。 图4 机翼整体结构有限元模型 试验结果和初始有限元计算结果列于表6中,其中误差和MAC(Modal Assurance Criteria)可以分别由下式得到 (32) (33) 将机翼蒙皮和翼肋的弹性模量、厚度作为待修正参数,其修正区间取值范围见表4。 表4 机翼有限元模型修正参数的修正区间 通过MSC.NASTRAN对表5中每组样本点对应的有限元模型进行固有振动频率计算,定义F为结构前五阶固有频率测量值和计算值之间残差的绝对值与对应权系数乘积的总和: (34) (35) 表5 基于中心复合试验设计的机翼模型计算样本点和目标函数值 Tab.5 The calculate sample points and objective function values of wing model based on central composite experimental design 编号E1t-1E2t-2F1-1-1-1-134.42-1-0.33-0.33-0.3322.163-10.330.330.3311.24-11113.15-0.33-1-0.330.3333.526-0.33-0.330.33121.97-0.330.331-198-0.331-1-0.333.0490.33-1-0.330.3332.88100.33-0.330.33120.56110.330.331-18.74120.331-1-0.333.44131-1-0.330.3331.62141-0.330.33119.261510.331-17.31611-1-0.334.461711113.961810.330.330.338.14191-0.33-0.33-0.3318.28201-1-1-146.56210.3310.33-0.333.6220.330.33-0.33-18.66230.33-0.33-1121.16240.33-110.3332.4825-0.3310.33-0.333.226-0.330.33-0.33-19.5227-0.33-0.33-1122.4428-0.33-110.3333.7429-110.33-0.333.0230-10.33-0.33-110.3831-1-0.33-1123.7632-1-110.3335.02 最终得到的修正参数需要满足 (36) 根据式(19)构造代理模型,采用高斯基,并且增加一组多项式函数作为SVM-Multi的基函数,然后通过遗传算法计算获得最优解。由于权系数的大小会对修正结果产生直接影响,因此定义wi=1/n,使各阶固有频率对结果的影响是均匀的。修正前后有限元计算固有频率和试验测量固有频率的对比情况如表6所示。 表6 机翼结构前五阶固有频率试验值与计算值的相关性分析 Tab.6 The Correlation Analysis of experimental and calculated values of the first five natural frequencies 模态阶数固有频率/Hz试验修正前误差MAC修正后误差MAC1102.297.15.00.85100.02.150.992192.7181.94.00.82196.31.870.973237.9202.814.80.61236.20.710.964271.2228.915.60.09271.70.180.975302.1242.719.70.04301.40.230.98 通过对比可以发现,修正后结构的前五阶固有频率误差明显降低,特别是第三、四、五阶固有频率误差变化尤为明显,对应的MAC值也明显增大。 (a)修正前的MAC矩阵(b)修正后的MAC矩阵 图5 修正前后MAC矩阵对比图 Fig.5 The modal assurance criteria before and after model updating 图5为试验模型分别与修正前后的有限元模型前5阶振型的MAC图,从图中可以看出,修正前的MAC矩阵对角元数值不大,某些非对角元数值较大,说明修正前的有限元模型与试验模型相关性不好;而修正后的MAC矩阵对角元几乎为1,非对角元也相对较小,说明修正后的有限元模型与试验模型相关性比较好。 3.3 典型连接结构动力学模型修正 本算例选取一种典型的螺栓联接结构——板搭接件作为研究对象进行研究,试验装置如图6(a)所示,采用bush单元模拟螺栓,有限元模型如图6(b)所示。 (a) 搭接板锤击试验 (b) 搭接板有限元模型 图6 搭接板锤击试验与搭接板有限元模型 Fig.6 The lap board hammer test and finite element model of lap board 将 bush单元的轴向平动刚度k作为模型修正参数之一,将材料的弹性模型E作为另一个修正参数。表7给出了修正参数的修正区间。 表7 搭接板结构修正参数的修正区间 本算例采用全面析因试验设计方法构造样本点,将各阶试验测量固有频率与有限元计算固有频率之间的残差fi作为目标函数 (37) 本算例采用Pareto优化算法,将结构动力学模型修正问题转化成对优化问题(38)的求解过程 (38) 通过SVM-Multi构造代理模型,搭接板前四阶弯曲模态频率残差绝对值的代理模型,如图7所示。 通过MATLAB优化工具箱计算可以得到一组的最优解集,这些最优解构成的Pareto前缘,如图8所示。 通过多目标优化得到一组最优解集,根据各个解计算得到的固有频率与测量值之间的偏差列于表9中,可以看出,固有频率的最大偏差不超过0.76%,最小偏差仅有0.002%,这表示修正后搭接板有限元模型的动力学特性与真实结构具有良好的一致性。 表8 基于全面析因试验设计的搭接板计算样本点和目标函数值 Tab.8 The calculate sample points and objective function values of lap board based on central composite experimental design 样本点kEf1f2f3f41-1-13.811.4828.436.162-1-0.333.340.2225.920.163-10.332.871.8923.455.934-112.423.5521.0111.645-0.33-10.341.458.075.876-0.33-0.330.230.245.040.147-0.330.330.801.922.056.088-0.3311.363.580.9111.9690.33-10.231.454.275.82100.33-0.330.810.251.130.19110.330.331.401.931.986.13120.3311.983.585.0512.01131-10.471.452.645.80141-0.331.070.250.560.211510.331.661.933.716.1516112.253.596.8312.04 (a)代理模型f1(b)代理模型f2 (c)代理模型f3(d)代理模型f4 图7 前四阶代理模型 Fig.7 The first four agent model 本文对传统SVM进行改进,提出了一种基于混合基函数的增广SVM方法,并以此为基础构造代理模型来实现结构动力学模型修正。通过Branin rcos函数的数值算例来对比验证增广SVM的预测精度,并通过机翼模型仿真算例和搭接板动力学试验算例来证明基于增广SVM的结构动力学模型修正方法的实用性,算例结果表明: 图8 Pareto前缘 最优解集频率误差/%第一阶第二阶第三阶第四阶10.7550.1290.5050.00220.6850.0520.3390.07630.6470.0130.3720.11640.5910.0520.4250.18450.5310.1290.4820.26060.4840.2000.5220.32770.4640.2320.5390.36080.4490.2840.5420.41190.4430.2970.5490.427100.4490.3160.5350.447110.4560.3480.5180.480120.4730.3740.4950.500130.4980.3870.4590.517140.5130.3940.4390.522150.5310.4000.4150.526160.5450.3360.3950.531170.5730.4070.3620.525180.5960.4070.3320.537190.6100.4130.3180.538200.6270.4130.2920.538 (1) 本文提出的混合基增广SVM有效解决了传统SVM存在的过拟合或者拟合精度不足的问题,可用于构造具有良好预测精度的代理模型; (2) 算例分析结果表明,在增广SVM的基础上提出的模型修正方法对试验样本数的需求较少,可以在少量试验数据样本的条件下获得具有高计算精度的修正模型; (3) 由于增广SVM具有很好的泛化能力,可以准确逼近含有显著非线性特征的真实响应,因此本文提出的模型修正方法也适用于具有较高非线性特征的结构动力学模型修正问题。 [1] MOTTERSHEAD J E, FRISWELL M I. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration, 1993, 167(2): 347-375. [2] BROWNJOHN J M W, DUMANOGLU A A, SEVERN R T. Ambient vibration survey of the Fatih Sultan Mehmet (Second Bosporus) suspension bridge[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(10): 907-924. [3] RODDEN W P. A method for deriving structural influence coefficients from ground vibration tests[J]. AIAA Journal, 1967, 5(5): 991-1000. [4] BERMAN A, FLANNELLY W G. Theory of incomplete models of dynamic structures[J]. AIAA Journal, 1971, 9(8): 1481-1487. [5] BALCI O.Verification validation and accreditation for simulation models[C].Proceedings of the 29th Conference on Winter Simulation,1997. [6] AESCHLIMAN D P,OBERKAMPF W L.Experimental methodology for computational fluid dynamics code validation[R].Sandia National Laboratories,Albuquerque,NM,1997. [7] KHURI A I, CORNELL J A. Response surface designs and analysis[M]. Marcel Dekker, Inc,1987. [8] MYERS R H, MONTGOMERY D C, ANDERSON-COOK C M. Response surface methodology: process and product optimization using designed experiments[M]. John Wiley & Sons, 2016. [9] MARWALA T. Finite-element-model updating using the response-surface method[J]. Finite-element-model Updating Using Computional Intelligence Techniques: Applications to Structural Dynamics, 2010: 103-125. [10] KRISHNAMURTHY T. Comparison of response surface construction methods for derivative estimation using moving least squares, kriging and radial basis functions[C]//Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conference, AIAA-2005-1821. 2005: 18-21. [11] KUMER S. Neural networks[M]. Beijing: Tsinghua University Press, 2006. [12] BUHMANN M D. Radial basis functions:Theory and Implementations[M]. Cambridge University Press, Cambridge, UK, 2003. [13] VAN BEERS W C M, KLEIJNEN J P C. Kriging interpolation in simulation: a survey[C]∥Simulation Conference, 2004. Proceedings of the 2004 Winter Simulation Conference:107-115. [14] CRESSIE N A C. Statistics for spatial data[M]. revised edition. New York:Wiley, 1993. [15] GUNN S R. Support vector machines for classification and regression[R]. ISIS technical report, 1998, 14. [16] VAPINK V. Statistical learning theory[M]. New York: Wiley,1998. [17] CLARKE S M, GRIEBSCH J H, SIMPSON T W. Analysis of support vector regression for approximation of complex engineering analyses[J]. Journal of Mechanical Design, 2005, 127(6): 1077-1087. [18] AYESTARAN R G, HERAS F L. Support vector regression for the design of array antennas[J]. IEEE Antennas and Wireless Propagation Letters, 2005, 4:414-416 [19] YUN Y, YOON M, NAKAYAMA H. Multi-objective optimization based on meta-modeling by using support vector regression[J]. Optimization and Engineering, 2009, 10(2):167-181. [20] SAQLAIN A, HE L S. Support vector regression-driven multidisciplinary design optimization for multi-stage space launch vehicle considering throttling effect[J]. 44th AIAA. Aerospace Sciences Meeting, 2006, 6:4089-4102. [21] WANG B P, DIVIJA O, LEE Y J. Structural optimization using FEMLAB and smooth support vector regression[C]. 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2007, 3:2568-2577. [22] QAZI M U D, HE L, MATEEN P. Hammersley sampling and support-vector-regression-driven launch vehicle design[J]. Journal of Spacecraft and Rockets, 2007, 44(5): 1094-1106. [23] WANG H, LI E, LI G Y. The least square support vector regression coupled with parallel sampling scheme metamodeling technique and application in sheet forming optimization[J]. Materials & Design, 2009, 30(5): 1468-1479. [24] 朱跃,张令弥,郭勤涛.基于SVR 方法的有限元模型确认中不确定性建模研究[J].振动与冲击,2010,29(3):190-196. ZHU Yue, ZHANG Lingmi, GUO Qintao. SVR based uncertainty modeling m ethod for structures finite element model validation[J]. Journal of Vibration and Shock, 2010,29(3):190-196. [25] 朱跃,张令弥.基于确定性计算响应面的复杂工程结构不确定性建模研究[J].计算力学学报,2011,28(3):412-416. ZHU Yue, ZHANG Lingmi. Deterministic computer simulation response surface research on complex engineer structure uncertainty[J]. Chinese Journal of Computational Mechanics, 2011,28(3):412-416. [26] 费庆国, 张令弥, 李爱群, 等. 基于统计分析技术的有限元模型修正研究[J]. 振动与冲击, 2005, 24(3): 23-26. FEI Qingguo, ZHANG Lingmi, LI Aiqun,etal. Finite element model updating using statistics analysis[J]. Journal of Vibration and shock, 2005,24(3):23-26. [27] 张冬冬, 郭勤涛. Kriging响应面代理模型在有限元模型确认中的应用[J]. 振动与冲击, 2013, 32(9): 187-191. ZHANG Dongdong, GUO Qintao. Application of Kriging response surface in finite element model validation[J]. Journal of Vibration and Shock, 2013, 32(9): 187-191. [28] REN W X, CHEN H B. Finite element model updating in structural dynamics by using response surface method[J]. Engineering Structures, 2010, 32(8): 2455-2465. [29] VAPNIK V N. An overview of statistical learning theory[J]. IEEE Transactions on Neural Networks,1999,10(5):988-999. Structural dynamic model updating based on augmented SVM CHEN Zhe, HE Huan, CHEN Guoping (The State Key Lab of Mechanics and Control for Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China) Here, the FE model updating method based on surrogate model was studied. An augmented support vector machine (SVM) based on hybrid basis functions was proposed for solving over-fitting results when SVM was used to deal with weak nonlinear functions. Based on dynamic test results measured and calculated results with a structural finite element model, according to design requirements, sensitivity analysis or engineering experience, appropriate parameters to be modified and modification ranges were chosen to determine the modification sample space and sample points. Then, the surrogate model for each group of sample points and corresponding objective function was constructed adopting the augmented SVM. The multi-objective optimization algorithm based on Pareto optimal solution was introduced to find the global optimal solution to parameters to be modified within the modification interval taking the output of the surrogate model as the objective and the sample space as variables. Example 1 showed that the prediction results with the augmented SVM have a higher accuracy than those with the traditional SVM do. Example 2 and 3 showed that the structural dynamic model updating based on the proposed augmented SVM is valuable in actual application and its results have a higher precision. surrogate model; multi-objective optimization; augmented SVM; model updating 国家自然科学基金(11472132); 江苏省研究生培养创新工程(KYLX_0223);中央高校基本科研业务费资助(NS2014002); 江苏高校优势学科建设工程 2015-11-30 修改稿收到日期:2016-06-16 陈喆 女,博士生,1989年6月生 何欢 男,博士,副教授,1978年2月生 O327 A 10.13465/j.cnki.jvs.2017.15.029

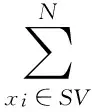
2 基于增广SVM的模型修正
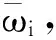
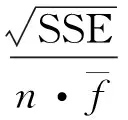
3 数值仿真验证

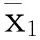















4 结 论