复杂移动轮胎力作用下沥青路面黏弹性力学行为模拟研究
2017-08-30王丽娟路永婕司春棣
王 扬, 王丽娟, 路永婕, 司春棣
(1. 石家庄铁道大学 土木工程学院, 石家庄 050043;2. 河北省交通安全与控制重点实验室, 石家庄 050043)
复杂移动轮胎力作用下沥青路面黏弹性力学行为模拟研究
王 扬1, 王丽娟2, 路永婕2, 司春棣2
(1. 石家庄铁道大学 土木工程学院, 石家庄 050043;2. 河北省交通安全与控制重点实验室, 石家庄 050043)
对复杂移动轮胎力作用下的沥青路面黏弹性有限元建模进行了分析与探讨,在此基础上对路面的黏弹性力学行为进行了仿真,并分析了轮组形式和轴组形式对路面响应的影响。研究表明,在移动轮胎力作用下的路面有限元模型中,沥青混合料的蠕变法则宜采用应变硬化率关系式;在轮胎力反复作用下,路面内部的应力分布趋于均匀,中面层承受较大的Tresca应力;在轮胎工作状态相同的条件下,单轮组对路面永久变形的贡献与双轮组同等重要,双轴组对路面的破坏效应比单轴组更加显著。
沥青路面; 黏弹性力学行为; 复杂移动轮胎力; 有限元分析
路面在车辆荷载作用下的力学行为是其结构设计和材料设计的基础。长期以来,路面力学行为分析多以静态垂向轮胎力作用下的路面结构为研究对象进行研究,在一定程度上揭示了路面结构的力学行为特征。但是,实际的轮胎力是移动的三向荷载,将其简化为静态垂向轮胎力进行分析,难以准确反映路面力学行为的真实状态[1]。因此,研究移动复杂荷载重复作用下的路面力学行为,推动路面结构设计从静态向动态转化,已成为目前道路工程领域的热点问题之一[2]。
Al-Qadi等[3]基于有限元分析得到了三向复杂轮胎力的空间分布,并将其施加于路面模型,分析了车辆轴载和轮胎胎压对路面的影响。Wang等[4]建立了非线性各向异性的路面有限元模型,分析了移动车辆荷载作用下黏弹性路面的力学响应。
董泽蛟等[5]对非均布移动荷载作用下沥青路面的动力响应进行了有限元分析,并结合现场实测结果,分析了路面动力响应的空间分布和时程变化规律。胡小弟等[6]采用实测的垂向轮胎力对路面模型进行加载,分析了车辆在不同运动状态下相关因素对路面响应的影响。
Wollny等[7]、Xia等[8]、Wang等[9]分别建立了轮胎-路面耦合模型,实现了轮胎对路面的直接作用,并基于耦合模型进行了路面的力学响应分析。
部分学者针对移动荷载作用下的车辙预估方法进行了探索。Zhu等[10]提出了基于两阶段黏弹塑性损伤本构模型的沥青路面车辙预测方法,Zopf等[11]采用一个Maxwell单元和两个分数Maxwell单元描述沥青混合料的黏弹性行为,对车辙进行了预测。
以上研究成果针对不同的轮胎力形式进行了路面响应及永久变形的仿真,获得了一系列有意义的研究结论。但是,上述成果没有针对车辆的特征进行具体分析。本文通过建立移动轮胎力作用下的三维路面模型,在分析路面黏弹性力学响应的基础上,揭示车辆轮组形式和轴组形式对路面力学行为的影响。
1 有限元模型的建立
1.1 路面结构
以G45高速公路某段的路面结构为原型,基于ABAQUS软件建立路面模型,如图1所示。考虑到面层分为三层铺筑,并且各层沥青混合料的组成互不相同,因此将模型中的面层划分为三个结构层,即上面层、中面层、下面层。模型X轴方向为行车方向,Y轴方向为路面横向,Z轴的负方向为深度方向。
模型X,Y,Z三个方向的长度分别为4 m、4 m、3 m,在YOZ平面内的网格化分如图1(b)所示。路面结构采用位移边界条件,即:纵向两侧X方向位移为0,横向两侧Y方向位移为0,底部Z方向位移为0。

(a) 模型外观

(b) 模型网格
1.2 材料模型的选择及参数设置
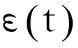
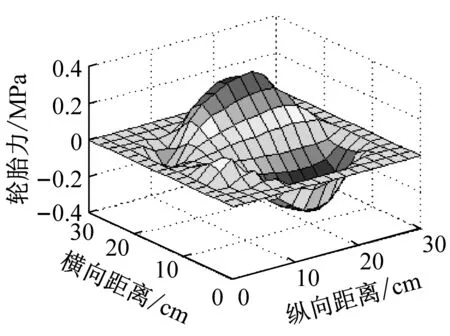
ε(t)=εe+εc
(1)
式中:εe与时间无关,εc是时间t、温度T及应力σ的函数。假设在车辆荷载作用下,沥青混合料处于主蠕变区,在温度固定的条件下,εc可表示为[12]

(2)
式中:A,m,n均为材料的蠕变参数。
将式(2)对时间微分可获得蠕变应变率

(3)
式(3)即为时间硬化率关系式,一般用于恒定负载下的蠕变分析。对于非恒定负载下的蠕变分析,通常采用与时间无关的应变硬化率关系式,即
可见,式(4)中的蠕变应变率与应力和蠕应变的累积量相关,而与时间无关。
本文所建立的模型中,轮胎力为移动荷载,故应采用应变硬化率关系式描述沥青混合料的力学行为。对于其他路面材料,均选用线弹性本构关系。路面结构参数及材料参数,如表1所示。

表1 路面结构参数及材料参数
1.3 轮胎荷载的施加
本文针对单轴单轮组、单轴双轮组、双轴双轮组等三种形式的轮胎力进行分析,双轮组的轮胎间距为346 mm,双轴组的轴距为1.3 m。根据文献[13],当货车或挂车的轴组形式为单轴时,每侧单胎和每侧双胎的车轴最大允许轴荷分别为60 kN和100 kN;并装双轴车辆装配的轮组形式为双轮组,当轴距为1.3 m时,双轴组的最大允许轴荷为190 kN。我国路面设计以双轮组单轴载100 kN作为标准轴载,其中每个轮胎承重25 kN[14-15]。以路面设计的标准轴载为参照,综合考虑车辆设计规范,确定本文中的单胎承重25 kN,则三种轮胎力对应的车辆荷载分别为25 kN、50 kN、100 kN。进一步假定轮胎充气胎压为0.72 MPa、以80 km/h自由滚动,文献[16]对此工况下的单轮组轮胎进行了稳态滚动分析,得到的三向轮胎力空间分布形式,如图2所示。假定单轴单轮组、单轴双轮组、双轴双轮组中单个轮胎的工作状态完全相同,故文中的三种轮胎力中,单个轮胎的轮胎力形式均与图2相同。

(a) 垂向轮胎力
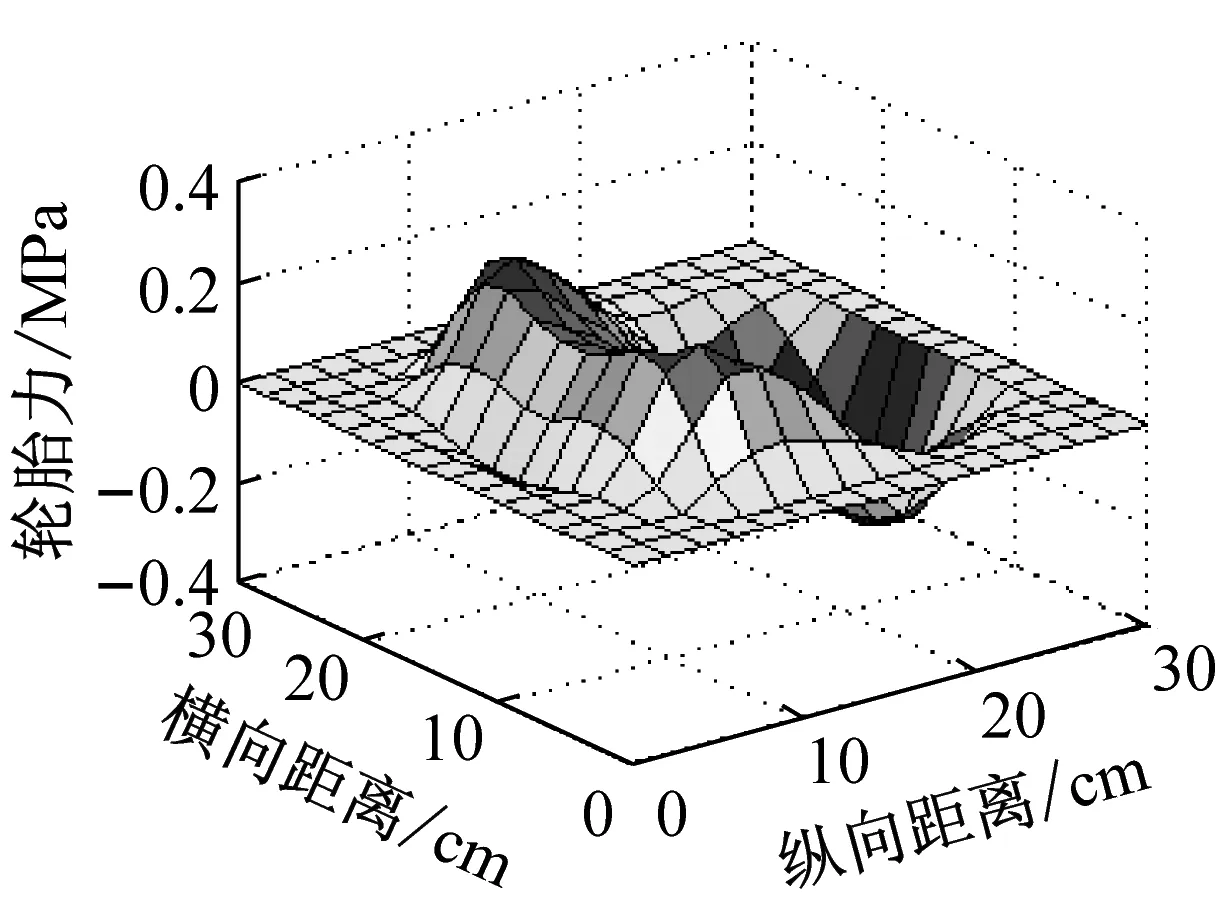
(b) 纵向轮胎力
(c) 侧向轮胎力
采用ABAQUS软件的用户子程序实现轮胎力对路面的反复作用,其中垂向接触力通过DLOAD加载,水平向接触力通过UTRACLOAD加载。在此以单轴双轮组轮胎力为例,说明轮胎力的加载过程。轮胎力关于X轴对称,在每一个加载过程内,轮胎力沿X轴正方向在路表移动,如图3所示。在X方向距路面边界0.5 m以内为轮胎力加载区域,轮胎力由路面左侧以80 km/h的速度匀速运动至右侧完成一次加载,耗时t1。轮胎力加载结束后,仿真仍继续一段时间t2,使路面材料变形充分恢复。单次加载过程的时间长度T=t1+t2,综合考虑求解效率及实际轮胎力的加载时间间隔,确定T=0.25 s。

图3 加载过程中轮胎力的平面位置及特征剖面
2 仿真结果与分析
以图3中的A-A剖面和B-B剖面作为特征剖面,其中A-A剖面是轮胎-路面接触区中心点移动轨迹所在的断面,B-B剖面是路面x=2 m处的模型横断面。以路面各结构层底部与A-A剖面及B-B剖面的交点作为特征点,上面层、中面层、下面层、基层、底基层底部的特征点依次记为a,b,c,d,e。上述特征剖面和特征点用于输出路面的应力,另将路表与A-A剖面及B-B剖面的交点记为f,用于输出路表的垂向位移。
2.1 单轴双轮组轮胎力作用下的路面力学响应
采用单轴双轮组轮胎力对路面加载20次,路面特征点所在单元的Tresca应力时程变化如图4所示,图4表明,路面在轮胎力反复作用下的力学响应呈现出如下特征:① 总体上,a点自加载初期至卸载到0.1 MPa之前、b点和c点自加载初期至卸载到0.05 MPa之前,应力的变化率处于较高水平,d,e两点在整个加载-卸载过程中的应力变化率均处于较高水平。在以上应力变化范围内,a,b两点的应力变化率差别不大,b,c,d,e四点的应力变化率依次降低,即应力的变化率随深度的增加而减小。② 在每次加载-卸载过程中,各特征点在相同时刻出现应力的峰值。除初期的加载过程外,各特征点的应力峰值基本稳定,且应力峰值随深度的增加而减小。a点和b点的应力峰值在0.4 MPa左右,c,d,e三点的应力峰值分别为0.2 MPa、90 kPa和60 kPa。考虑到d,e两点应力幅值相对较低,且其材料为线弹性,故在以下的分析中不再对其进行讨论。③ 总体上,a点卸载到0.1 MPa之后、b点和c点卸载到0.05 MPa之后,应力的变化率逐渐减小。当卸载结束后,材料内部仍存在残余应力。越靠近路表,残余应力的消散越缓慢。在此阶段的力学行为特征,是由于材料的黏弹性导致的。

(a) a点
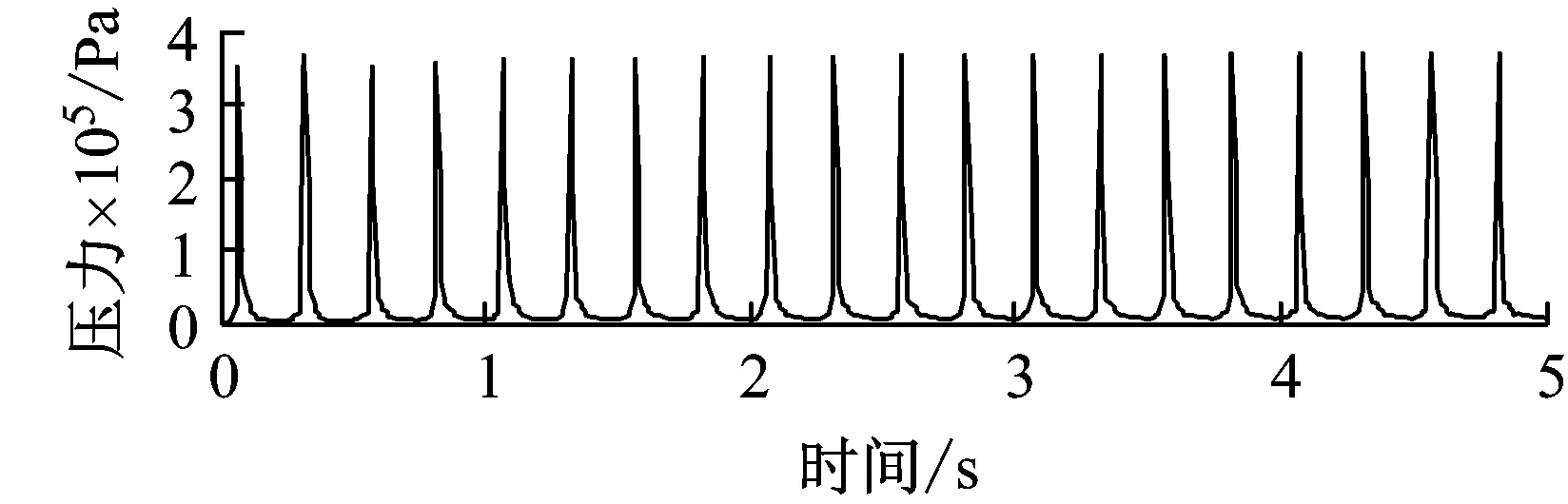
(b) b点
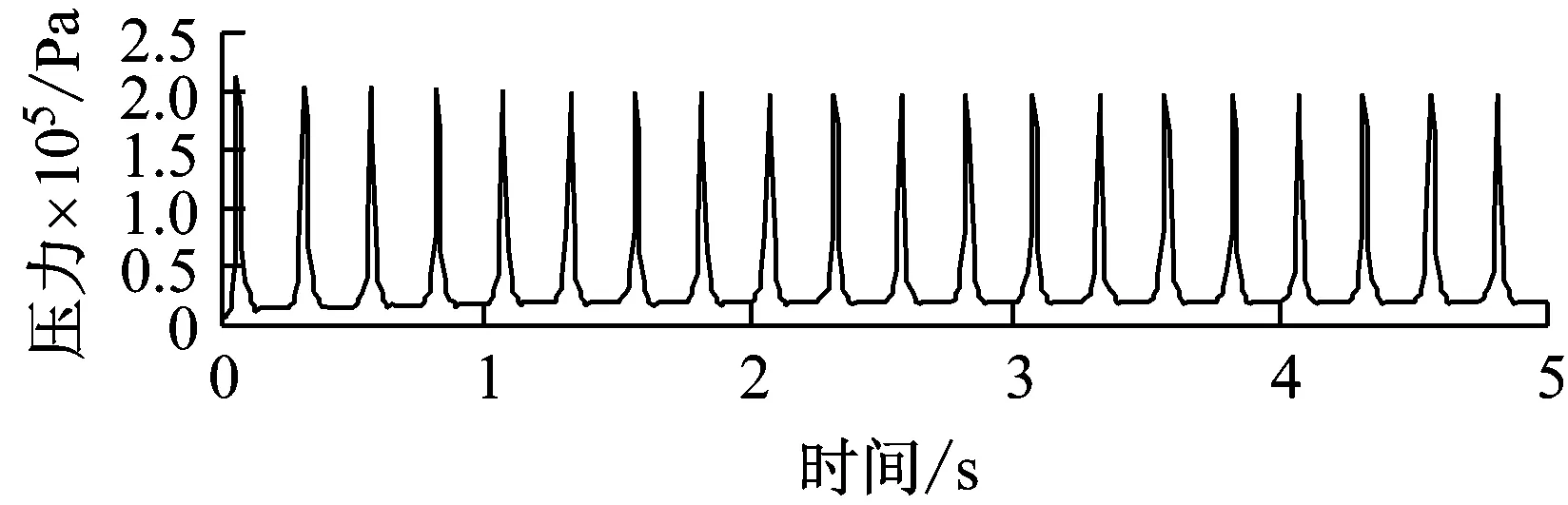
(c) c点

(d) d点

(e) e点
Fig.4 Time history variation of Tresca stress for characteristic points under wheel load of a daul-wheel set
仿真结果显示,随着轮胎力加载次数的增加,路面内部Tresca应力的空间分布逐渐变化。在此选取第1、5、10、20次加载进行分析,当轮胎力作用在特征点上方时,特征剖面Tresca应力的空间分布如图5所示。图5表明,在轮胎力多次快速作用下,面层材料的黏弹性导致Tresca应力的空间分布呈现以下特征:① 在加载初期,Tresca应力的空间分布明显不均匀,上面层底部承受了较大应力。随着荷载作用次数的增多,Tresca应力的空间分布才逐渐趋于均匀。图4中面层材料Tresca应力峰值在加载初期的波动特征即与此有关。② 在加载初期,上面层底部存在明显的残余应力,在第5次加载过后,上面层的残余应力即降低至较低值。③ 轮胎力第20次加载时,路面内部Tresca应力的分布接近均匀材料的Tresca应力分布特征。可以预见,在轮胎力长期反复作用下,中面层将承受较大Tresca应力,必将导致中面层发生显著的永久变形。
轮胎力加载过程中,f点垂向位移的时程曲线如图6所示。图6显示,在轮胎力的加载-卸载过程中,路表迅速发生垂向位移;轮胎力卸载后,大部分垂向位移发生回弹,但路表存在残余变形;随着轮胎力加载次数的增加,位移的峰值及残余变形均逐步增大。
2.2 轮组形式对路面力学响应的影响
采用单轮组轮胎力对路面加载20次,其他参数保持不变,特征点所在单元的Tresca应力时程变化如图7所示。对比图4和图7可以发现,两种工况下,a,b,c三点的应力时程变化差异不明显。
在第20次加过程中,当轮胎力作用在特征点上方时,特征剖面Tresca应力的空间分布如图8所示。对比图5和图8可以发现,两种工况下,A-A剖面的应力空间分布差异不明显;B-B剖面中的应力云图有所差异,但其中应力集中部位的应力分布差别不大。
综上,轮组形式的变化既没有显著改变特征点的应力状态,也没有改变其荷载历史。因此可以认为,对于单轴车辆,面层的力学行为由单个轮胎的轮胎力决定,轮组形式对面层没有影响。

(a) 第1次加载
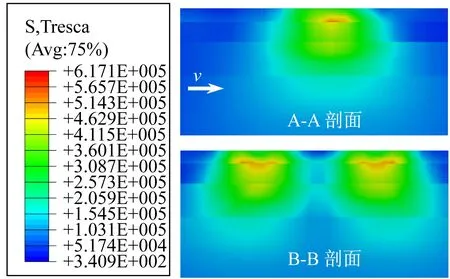
(b) 第5次加载
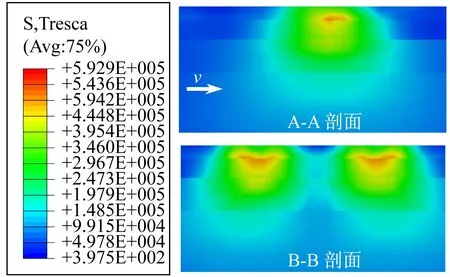
(c) 第10次加载
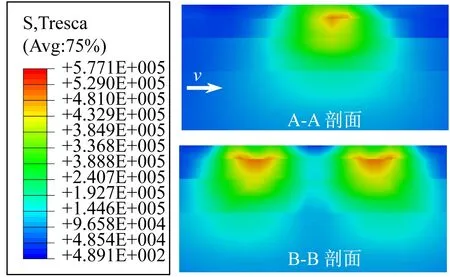
(d) 第20次加载
Fig.5 Spatial distribution of Tresca stress in characteristic sections under wheel load of a daul-wheel set
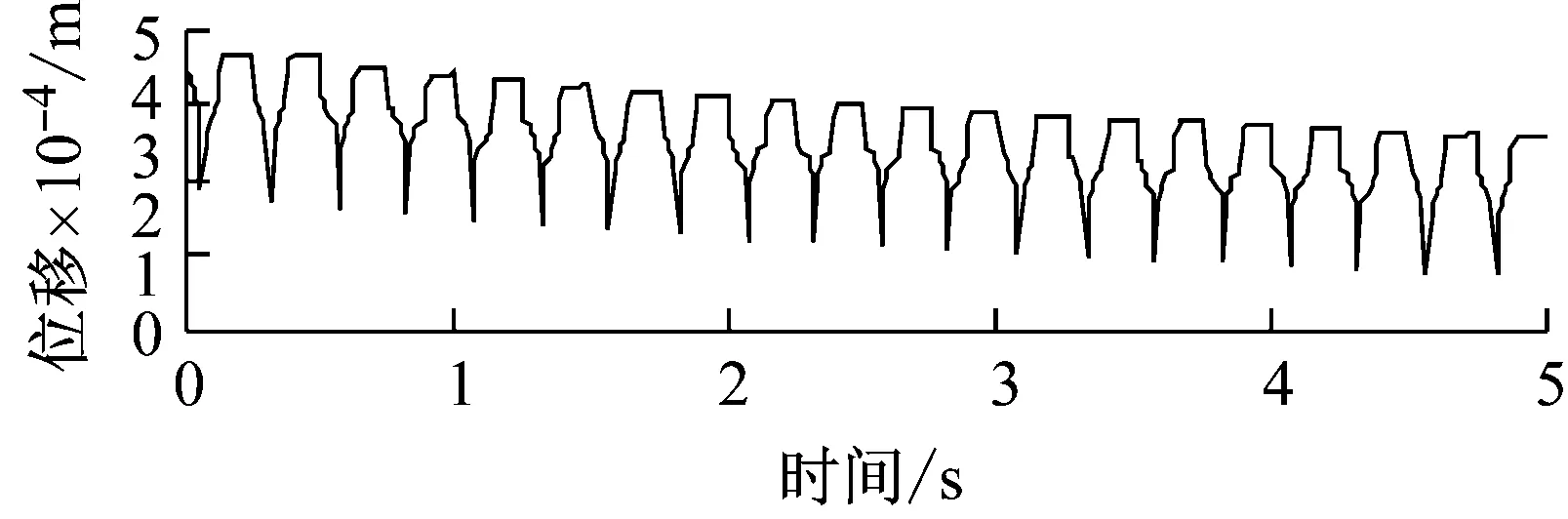
图6 单轴双轮组轮胎力作用下f点垂向位移的时程变化

(a) a点

(b) b点
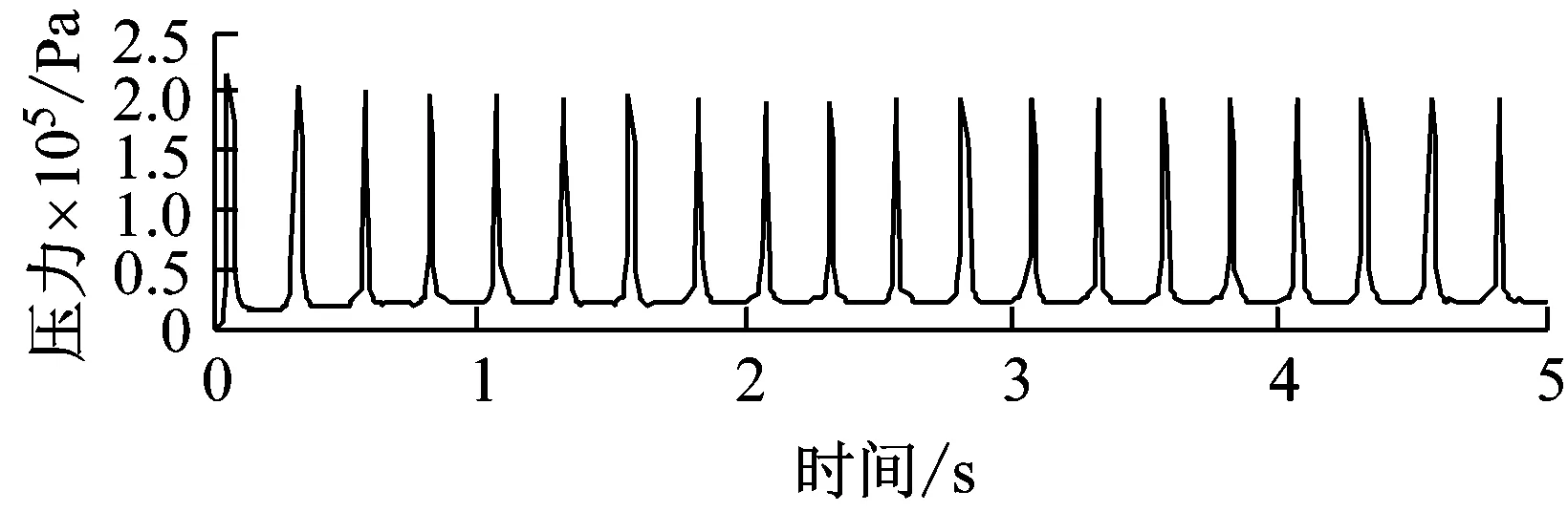
(c) c点
Fig.7 Time history variation of Tresca stress for characteristic points under wheel load of a single-wheel set

图8 单轮组轮胎力作用下特征剖面Tresca应力的 空间分布(第20次加载)
Fig.8 Spatial distribution of Tresca stress in characteristic sections under wheel load of a single-wheel set (the 20th loading)
轮胎力加载过程中,f点垂向位移的时程曲线如图9所示。对比图6和图9可以发现:① 单轮组作用下路表垂向位移的峰值较低。这是由于单轮组和双轮组轮胎力对应的车辆荷载分别为25 kN、50 kN,存在显著差异,故可以预见,单轮组作用时道路结构的弹性变形较小,最终表现为f点垂向位移的减小。② 图6和图9中的残余变形没有显著差异。由于蠕变应变仅与材料的应力状态和蠕应变的累积量相关,在两种工况下,材料应力和蠕应变的累积量均没有显著差异,残余变形也因此不会产生显著变化。
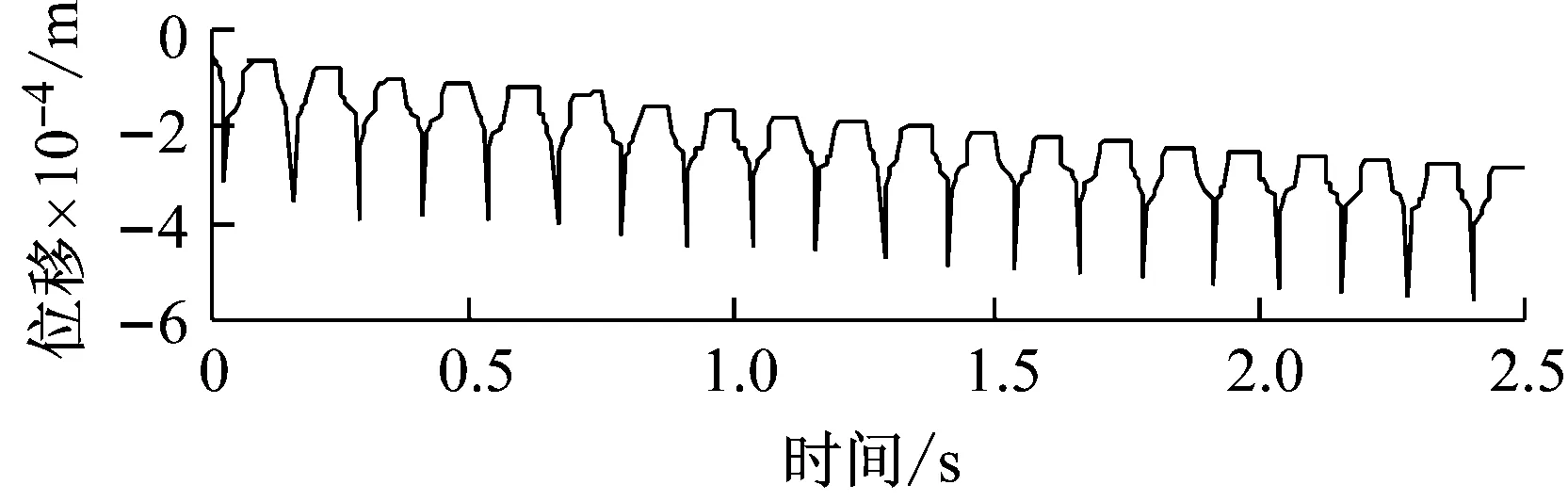
图9 单轮组轮胎力作用下f点垂向位移的时程变化
Fig.9 Time history variation of vertical displacement for pointfunder wheel load of a single-wheel set
2.3 轴组形式对路面力学响应的影响
采用双轴组轮胎力对路面加载10次,其他参数保持不变,特征点所在单元的Tresca应力时程变化如图10所示。对比图4和图10可以发现,轴组形式对路面力学响应具有显著影响,具体表现在以下方面:① 双轴组前轴轮胎力作用后,各点的应力尚未回复至平稳状态时,后轴轮胎力即进行了加载。路面承受双轮组轮胎力作用时,荷载历史与单轴组存在显著差异,因此导致了材料黏弹性力学响应的差异。② 双轴组前轴轮胎力作用下,a,b,c三点的应力峰值与单轴组作用时基本相同。③ 双轴组后轴轮胎力作用下,a,b两点的应力峰值显著增加,其中a点应力峰值的增加尤为显著;后轴轮胎力作用下,c点的应力峰值略有减小。
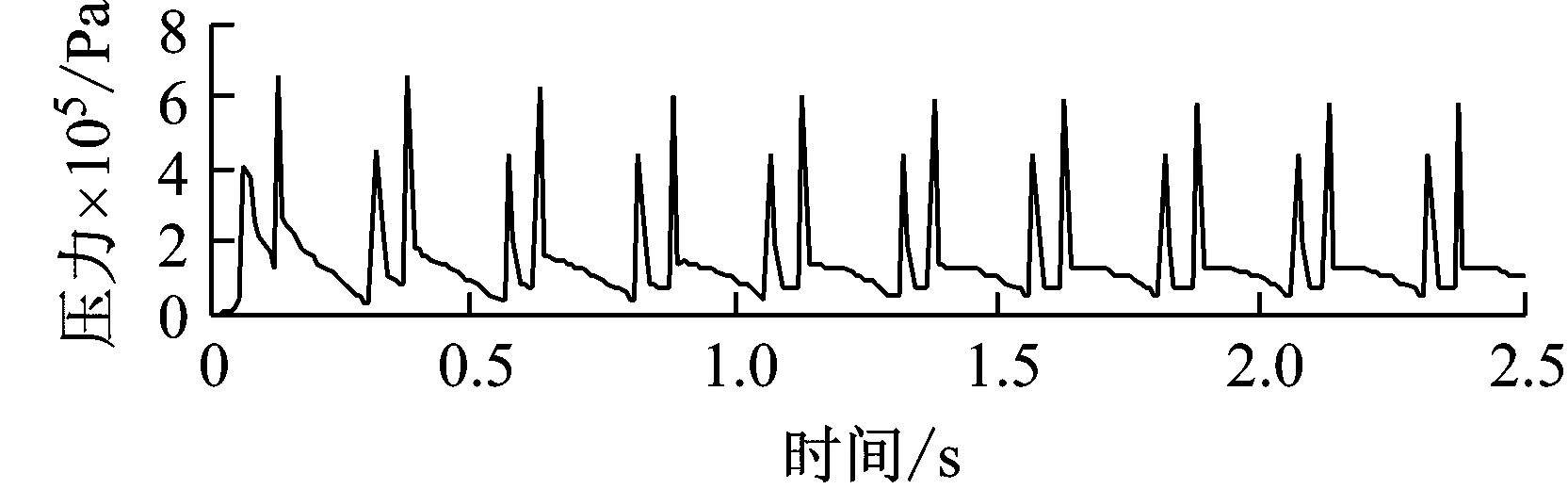
(a) a点

(b) b点

(c) c点
Fig.10 Time history variation of Tresca stress for characteristic points under wheel load of a daul-axle set
在第10次加过程中,当后轴轮胎力作用在特征点上方时,特征剖面Tresca应力的空间分布如图11所示。对比图5和图11可以发现:图11中的应力分布不如图5均匀,图11中A-A剖面上面层的残余应力明显大于图5。
轮胎力加载过程中,f点垂向位移的时程曲线如图12所示。对比图6和图12可以发现:① 双轴组后轴轮胎力作用时,前轴产生的应力尚未完全消散,因此导致图12中的残余变形高于图6。② 在产生较高的残余变形的同时,由于双轴组对路面施加了更大的车辆荷载,还导致了弹性变形的增加,故图12中的垂向位移峰值也高于图6。

图11 双轴组轮胎力作用下特征剖面Tresca应力的空间分布(第10次加载)
Fig.11 Spatial distribution of Tresca stress in characteristic sections under wheel load of a daul-axle set (the 10th loading)
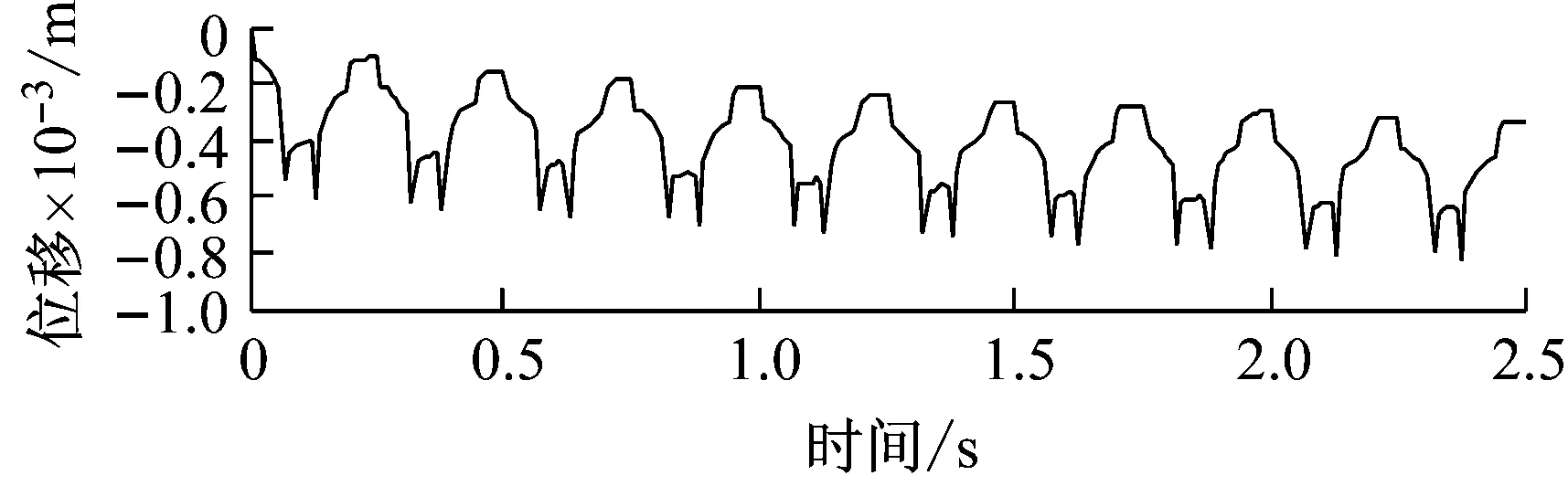
图12 单轮组轮胎力作用下f点垂向位移的时程变化
Fig.12 Time history variation of vertical displacement for pointfunder wheel load of a daul-axle set
3 结 论
基于复杂移动轮胎力作用下的沥青路面有限元模型,分析了路面的黏弹性力学行为,并进一步探讨了轮组形式和轴组形式对路面响应的影响,研究结论如下:
(1) 应变硬化率关系式中的蠕变应变率与时间无关,适用于非恒定荷载条件下的蠕变分析。由于移动轮胎力属于非恒定荷载,故路面模型中沥青混合料的蠕变法则宜采用应变硬化率关系式。
(2) 在轮胎力反复作用下,路面内部的应力分布趋于均匀,中面层承受较大的Tresca应力。
(3) 在轮胎工作参数相同的条件下,单轮组轮胎力与双轮组轮胎力作用下的路面黏弹性响应没有本质上的差异,表明单轮组对路面永久变形的贡献与双轮组同等重要。
(4) 在轮胎工作参数相同的条件下,相对于单轴组,双轴组使路面产生了更大的残余变形,表明双轴组车辆比单轴组车辆对路面的破坏效应更加显著。
[1] 裴建中, 吴浩, 陈勇, 等. 多轴移动荷载下沥青路面的动态响应特性[J]. 中国公路学报, 2011, 24(5): 26-31.
PEI Jianzhong, WU Hao, CHEN Yong, et al. Dynamic response characteristics of asphalt pavement under multi-axle moving load[J]. China Journal of Highway and Transport, 2011, 24(5): 26-31.
[2] YANG S P, CHEN L Q, LI S H. Dynamics of vehicle road coupled system[M]. Springer-Verlag, Berlin, 2015.
[3] AL-QADI I L, WANG H. Prediction of tire pavement contact stresses and analysis of asphalt pavement responses: A decoupled approach[J]. Journal of the Association of Asphalt Paving Technologists, 2011, 80: 289-316.
[4] WANG Hao, AL-QADI I L. Importance of nonlinear anisotropic modeling of granular base for predicting maximum viscoelastic pavement responses[J]. Journal of Engineering Mechanics, 2013, 139(1): 29-38.
[5] 董泽蛟, 谭忆秋, 欧进萍. 三向非均布移动荷载作用下沥青路面动力响应分析[J]. 土木工程学报, 2013, 46(6): 122-130.
DONG Zejiao, TAN Yiqiu, OU Jinping. Dynamic response analysis of asphalt pavement under three-directional nonuniform moving load[J]. China Civil Engineering Journal, 2013, 46(6): 122-130.
[6] HU X,WALUBITA L F. Modeling mechanistic responses in asphalt pavements under three-dimensional tire-pavement contact pressure[J]. Journal of Central South University of Technology, 2011, 18(1): 250-258.
[7] WOLLNY I, BEHNKE R, VILLARET K, et al. Numerical modelling of tyre-pavement interaction phenomena: coupled structural investigations[J]. Road Materials and Pavement Design, 2016, 17(3): 563-578.
[8] XIA K, YANG Y. Three-dimensional finite element modeling of tire/ground interaction[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(4): 498-516.
[9] WANG Y, LU Y J, SI C D, et al. Tire-pavement coupling dynamic simulation under tire high-speed-rolling condition[J]. International Journal of Simulation Modelling, 2016, 15(2): 236-248
[10] ZHU H, SUN L. Mechanistic Rutting prediction using a two-stage viscoelastic-viscoplastic damage constitutive model of asphalt mixtures[J]. Journal of Engineering Mechanics, 2013, 139(11): 1577-1591.
[11] ZOPF C, GARCIA M A, KALISKE M. A continuum mechanical approach to model asphalt[J]. International Journal of Pavement Engineering, 2015, 16(2): 105-124.
[12] PERL M, UZAN J, SIDES A. Visco-elasto-plastic constitutive law for a bituminous mixture under repeated loading[C]// McLaughlin M. Asphalt Materials, Mixtures, Construction, Moisture Effects and Sulfur. Washington, D. C.: Transportation Research Board, National Research Council, National Academy of Sciences, 1983. 20-27.
[13] 道路车辆外廓尺寸、轴荷及质量限值:GB 1589—2004[S].北京: 中国标准出版社, 2004.
[14] 公路沥青路面设计规范:JTG D50—2017[S]. 北京: 人民交通出版社, 2017.
[15] 城镇道路路面设计规范:CJJ 169—2011[S]. 北京:中国建筑工业出版社, 2011.
[16] 王扬. 复杂轮胎力作用下沥青路面力学行为研究[D]. 北京:北京交通大学, 2017.
Simulation on viscoelastic behavior of asphalt pavement under complex moving wheel load
WANG Yang1, WANG Lijuan2, LU Yongjie2, SI Chundi2
(1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. Key Laboratory of Traffic Safety and Control in Hebei, Shijiazhuang 050043, China)
A finite element model of pavement under the complex moving wheel load was established. Subsequently, viscoelastic behavior simulation of pavement was conducted, and the influence of wheel set and axle set on pavement response was analyzed. Results indicate that the strain-hardening formulation is suitable for the creep rule of asphalt mixture in the proposed model. Under the repeated impact of moving wheel load, the distribution of stress in the pavement tends to be uniform, and the intermediate pavement layer is subjected to a large Tresca stress. Under the same tire operating condition, the single-wheel set makes the same contribution to the permanent deformation of pavement with the dual-wheel set, and the damage effect of daul-axle set on pavement is more significant than that of single-axle set.
asphalt pavement; viscoelastic behavior; complex moving wheel load; finite element analysis
国家自然科学基金(11302138;11572207;11472180)
2017-04-06 修改稿收到日期:2017-05-07
王扬 男,博士,副教授,1979年8月生
TH212; TH213.3
A
10.13465/j.cnki.jvs.2017.15.027
