高温环境下结构动力学模型修正方法研究
2017-08-30袁昭旭于开平
袁昭旭, 于开平
(哈尔滨工业大学 航天学院,哈尔滨 150001)
高温环境下结构动力学模型修正方法研究
袁昭旭, 于开平
(哈尔滨工业大学 航天学院,哈尔滨 150001)
提出了一种新的基于贝叶斯参数估计的高温环境动力学模型修正方法,利用此方法对一复合材料层合板模型进行了修正。该方法的主旨在于,利用高温环境下的模态频率试验数据修正有限元模型。该方法的特点在于,可以通过参数和响应的离散度来描述其不确定性,从而更加合理地解决实际问题。在研究中,进行了高温环境下复合材料结构的动力学试验,通过试验得到其高温环境下的模态频率。以此为基础,对复合材料有限元模型进行修正。在修正前,对模型进行了灵敏度分析,探讨了参数与高温环境动力学响应之间的关系。根据试验所得数据和对待修正参数的预估设置其对应的离散度。利用自编译程序进行修正计算。通过修正,模型的温度-固有频率对应关系得到了明显的改善,证明了方法的有效性,可以适用于工程实际问题。
高温环境结构动力学;模型修正;复合材料;灵敏度分析
近几十年来,高超声速飞行器的动力学问题一直为研究者们所关注。文献[1-7]高超声速飞行所带来的高温环境对于结构的动力学特性有着较大的影响,故高温环境结构动力学是一项重要的研究课题。本文提出了一种新的基于贝叶斯参数估计的模型修正方法,并将其应用于复合材料层合板模型的修正工作中。
对于高温环境下的动力学问题,学者们进行了很多基础性的研究。Bailey[8]研究了当存在热应力影响时不同边界条件下板的振动问题,他考虑了在非耦合情况下各向异性板的情况。Chang等[9-10]进一步研究了耦合情况下考虑大变形非线性的热弹性动力学问题。Brown[11]通过实验和数值仿真的手段,研究了X-34 FASTRAC复合材料喷嘴的高温动力学特性。针对复合材料板、壳结构的研究也有很多进展[12-13]。
在反问题领域,学者们对高温环境结构的参数辨识也进行了大量的研究。这些研究分为两个主要方面,一方面是对热物理参数的辨识[14-18],一方面是对高温环境下热弹性参数的辨识[19-21]。其中,前者主要是针对研究热传导问题,并不是本文的重点。
热弹性动力学问题,其实质是热与弹性的耦合问题。但是在实际研究中,可以简化为热对弹性的单向耦合,即所谓高温结构动力学问题。高温环境对于结构动力学特性的影响主要来自两个方面:①温度对材料属性的影响,主要是材料的弹性模量受较高温度的影响会减小,随之改变的是结构的整体刚度;②温度梯度引起的结构的热应力会造成一定的结构附加刚度。结构刚度受热环境的影响往往会造成结构固有频率的下降,并在一定程度上缩小各阶固有频率之间的差距,进而影响结构的振动特性[22-23]。
在实际工程中,常常使用有限元等数学模型来对系统的动力学特征及相应进行预示。但是由于数学模型本身以及建模者的因素总会造成一定的误差,这种误差体现在数学模型与试验模型之间的不吻合。为了提高有限元模型的预示精度,学者们提出了模型修正的概念。利用试验数据对模型进行修改,从而使有限元模型与试验模型更加吻合。从20世纪80年代开始,模型修正的基础理论开始逐步形成,并延伸出大量的方法。 Mottershead等[24-25]对这些方法进行了系统的总结,在此不再复述。近些年来,模型修正问题的一个热门方向是基于不确定性的模型修正方法的研究[26-29]。这一方面研究方法有很多,包括概率型的[30]、非概率型的[31-32]。其中基于贝叶斯参数估计的方法,由于可以将试验与仿真二者的不确定性同时考虑入模型修正流程,被广泛使用于模型修正问题的研究[33-36]。
对于高温环境下的模型修正方法,目前的研究还很少[41]。Humbert等[37]提出了基于热弹性场的修正方法,这种方法强调了热应力对结构动特性的影响,但是由于热弹性场本身的测试有一定难度,故工程应用价值有限。Cheng等[38-39]提出了高温环境分级模型修正方法,将温度场参数和结构物理参数分为两个级别进行修正。Sun等[40]利用模型修正的方法,对结构热参数进行了辨识,在他的研究中考虑了材料热物理参数随温度变化的特性。在这些研究中,都没有将参数和试验响应的不确定性考虑进去,而本文提出的基于贝叶斯理论的修正方法弥补了这项空白。同时,现有的方法都是针对传统各向同性材料的,本文研究了在复合材料结构的高温环境模型修正方法,其响应和参数特性更加复杂。
1 高温环境结构动力学基础
从原理上来讲,高温环境对结构振动特性的影响归根结底是对结构整体刚度矩阵的影响。考虑结构整体刚度受温度影响主要有两方面:一方面在高温环境下,材料弹性模量E将随温度的改变而发生较大幅度的变化,进而改变了结构本身的整体刚度。在高温环境下,结构的刚度矩阵与常温刚度矩阵具有相同的形式:
(1)
式中:B为几何常数矩阵,由结构及其约束形式确定;D是结构的弹性常数矩阵,只与结构材料弹性模量E以及泊松比μ有关。当温度变化时弹性模量随之变化,则矩阵D也将随之改变。
另外,结构在高温环境下不可避免的会在内部产生温度梯度,这将会引起结构内部一定的热应力,进而产生附加的初始应力刚度矩阵改变结构整体刚度分布。以下简单介绍附加刚度矩阵的形成。
弹性体受温度载荷将产生初应变ε0,在弹性应力的作用下产生弹性应变D-1σ,弹性体的总应变ε是这两者的和,即
ε=D-1σ+ε0
(2)
式中,{σ}是考虑变温影响的弹性应力,也就是热应力。
σ=D(ε-ε0)
(3)
综上,结构的热刚度矩阵为:
K=KT+Kσ
(4)
该式即为结构热振动问题的有限元计算中所用到得结构受温度及温度梯度影响存在预应力情况下的总刚度矩阵。
从数学方法上,传统的模型修正方法多为基于灵敏度的方法。即通过微分方法或有限差分方法找到待修正参数与目标响应之间的微分关系,然后通过建立修正方程求解待修正参数的改变量。基于灵敏度的方法关键是要寻找修正参数与动力学响应之间的关系。即修正方程:
ΔR=SΔP
(5)
式中:S为灵敏度矩阵;ΔP为修正参数改变量向量;ΔR为有限元与试验响应之间的残差向量。对于高温环境模型修正,修正参数可以选择为材料刚度随温度改变率、材料热膨胀系数等热物理参数,也可以选择为温度场分布、应变场等热载荷变量。对于修正目标响应,可以选择为热模态频率及对应的模态振型。需要注意的是,在求解灵敏度方程过程中,刚度阵对于热物理参数的微分关系应该分为两部分:
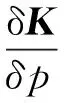
(6)
式中:γ=(ET-E0)/ΔT为材料刚度随温度变化率,α=(LT-L0)/ΔT为材料热膨胀系数。这两个参数为材料本身的物理属性,不会随外界条件所改变,可以作为修正参数。
2 基于贝叶斯参数估计的高温环境模型修正方法
对于修正方程的求解,学术界进行了大量的研究。比较适合本研究的是贝叶斯参数估计方法,现介绍其理论基础:
对于一个模型修正问题,可以写为如下修正方程的形式:
Re=Ra+S(Pu-Po)
(7)
或简写为:
ΔR=SΔP
(8)
式中:Re为参考系统响应向量(试验数据);Ra在参数向量{Po}情况下计算得到的响应向量;Pu为待求的修正后的参数向量;S为灵敏度矩阵。
这是基于灵敏度的模型修正方法的一般公式,其中对于灵敏度矩阵的求解一般是通过待求参数和响应之间的微分关系获得的。当待求参数和关心响应之间不易获得理论微分关系时,可以使用有限差分法获得对应灵敏度方程。
这个方程在一般情况下是超定的,对于传统的参数估计理论一般使用广义逆(最小二乘)方法求解。但是当需要考虑参数的不确定时,则可以使用贝叶斯参数估计方法。
根据贝叶斯参数估计理论,需要对待估计参数和响应同时进行加权处理,对应的加权误差可以写成如下形式:
E=ΔRTCRΔR+ΔPTCPΔP
(9)
这个误差可以通过如下算法得到最小值:
Pu=Po+G(-ΔR)
(10)
其中增益矩阵
G=(CP+STCRS)-1STCR
(11)
这个公式在响应个数多于参数个数时是有效的,当参数个数多于方程个数时,可以使用如下公式:
(12)
这个方程可以适用于参数个数多于方程个数的欠定方程的求解。
在上述方程中,权系数矩阵CP和CR分别表征了参数和响应的置信程度。在贝叶斯估计理论中称之为离散度(Scatter Value)。一般来讲,离散度可以通过统计量进行定义,这里使用定义公式:
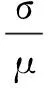
(13)
式中:μ为平均值;σ为标准差。对于离散度的选择可以按照如下原则:对于你认为置信程度低的参数设置较高的离散度,这样在方程求解过程中此参数可以发生较大改变;对于你认为置信程度高的参数设置较低的离散度,这样在方程求解过程中此参数不会发生较大改变。对于响应也是同样的道理。
贝叶斯方法的优点在于,可以同时引入待求参数和响应的不确定性。在此基础上,对式(10)进行反复迭代计算,以各阶计算固有频率与试验结果误差的平均值作为收敛标准,最终求解得到合理的修正结果。算法的整体流程如图1所示。
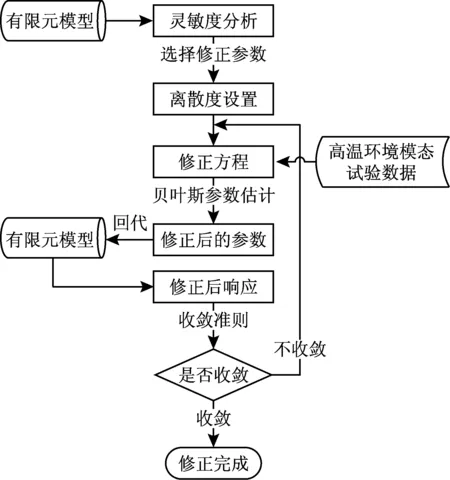
图1 修正算法流程
修正具体算法流程如下:
步骤1 初始化收敛系数ε>0,初始参数向量Po,离散度矩阵CP、CR;
步骤2 调用Nastran,计算响应残差向量ΔR;
步骤3 计算响应对参数的灵敏度矩阵S;
步骤4 根据式(10)计算修正方程,得到修正后参数向量Pu;
步骤7 输出Pu。
对于修正算法流程,做如下几点说明:
(1) 在模型修正流程开始之前,先要进行灵敏度分析,通过灵敏度分析的结果来选择合适的修正参数;
(2) 离散度的设置需要根据实际工程情况,其中参数的离散度是根据对参数的认识进行设定,试验数据的离散度是通过试验数据通过统计算法计算而得;
(3) 对于步骤3中灵敏度方程的求解,可以根据相关理论公式计算,或者利用有限差分方法进行计算;
(4) 对于步骤4的修正方程求解,可以根据参数与响应之间的个数关系来决定使用式(11)或式(12)进行参数估计。
对于一个模型修正算法,除了算法本身的性能之外,如何将其实现并应用于工程实际也是一项重要挑战。本文通过商用有限元模型修正软件FEMTools的二次开发功能,将所提出的算法嵌入到FEMTools修正流程中。
其中,对于FEMTools的自定义算法实现,有如下几个重点问题:
(1) 由于待修正参数中,有一些并不在FEMTools的标准库中,需要自定义修正参数,这可以通过parameter text path 'modal.bdf' line 1254 column 17 length 8 label 'TSM_E11' script 'bulk_format_8.bas'命令来实现;
(2) 对于自定义参数的实现,实质上是读取bdf文件中的对应行,但是需要注意的是,bdf中由于参数位数只能为8字节,需要自行编写一个脚本来处理卡片的数据,使其尽量不丢失精度;
(3) 由于热模态计算使用了Nastran的SOL106模块,需要编写自定义脚本,令FEMTools读取其计算结果op2文件,可以使用FEMTools的Ft_Import "mode", "nastran.bin", sOP2File命令来实现op2文件的读取。
(4) 具体实现方法,请参考FEMTools官方手册二次开发部分。
3 复合材料层合板高温环境振动试验
本研究的修正对象为碳纤维/双马树脂基复合材料层合板,采用试件由16层纤维铺设而成,铺层顺序[02/±45/02/90/0]s。尺寸为400 mm×300 mm,厚度2.4 mm。这是一种典型的层合板结构,被广泛应用于飞行器结构。
如图2,3所示,试验边界条件为单边固支。利用专用夹具将试验件固定在工作台面上,一面采用石英灯阵进行加热,另一面采用激振器进行激励。传感器与激振器均处于灯阵加热阴影中,这样可以保护设备。由于本实验关心高温环境下热应力对结构的影响,为了防止激振杆带来的连接刚度,采用随机脉冲载荷进行激励。随机脉冲激励是指,在传统冲击载荷的基础上,利用随机信号发生器创造连续的随机脉冲激励信号。当信号的功率谱能够完整覆盖所关心频段时,即可通过这种信号进行基于频响方法的模态参数辨识。其优点在于,相对传统脉冲激励,能够获得更加宽的激励频带,同时在安装上不需要跟试件连接,减小了连接刚度的影响。根据板型结构的模态振型特点,对于测试前三阶模态,在中线位置均匀布置三个传感器。所采用的传感器为PCB高温环境传感器,适用温度环境-60 ℃~240 ℃。
为了适应高温环境下的操作,采用耐高温胶对传感器进行粘贴安装。采用的耐高温胶温度适应范围为-60 ℃~300 ℃,可以满足本试验的需求。采用德国M+P振动测试仪进行试验数据的采集、处理。同时,利用M+P数字信号生成功能产生随机信号,经过功率放大器(江苏联能)放大后由激振器输出随机脉冲激励。通过石英灯阵的控制程序,输入设置温度对结构进行加热。同时打开激振器对结构进行激励,采集相关振动信号,对结构振动特性进行分析。

图2 试验概况

图3 试验概况
试验温度采用梯度增加的形式,在每个梯度段采集相关振动信号,温度曲线,如图4所示。
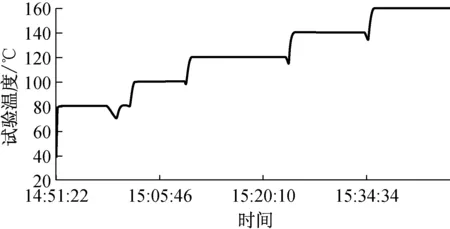
图4 试验温度曲线
本试验每个温度工况下至少进行五次数据采集,其中温度由常温最高升至180℃。利用M+P的基于频响函数的模态参数辨识方法进行模态参数辨识。如图5,其中三个颜色的频响曲线分别代表三个传感器得到的对应频响函数。
将识别出的各阶模态频率取平均数绘制曲线,如图6所示。

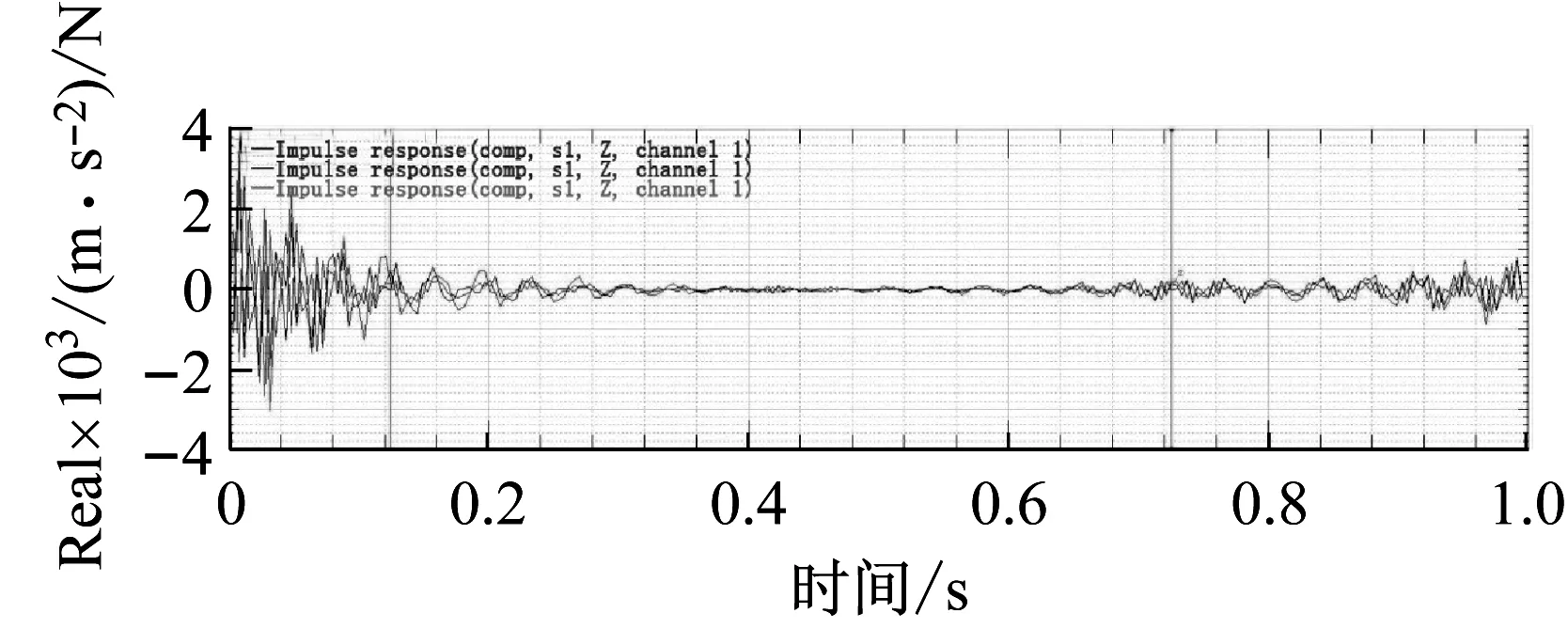
图5 在M+P中利用试验得到的频响函数进行模态辨识
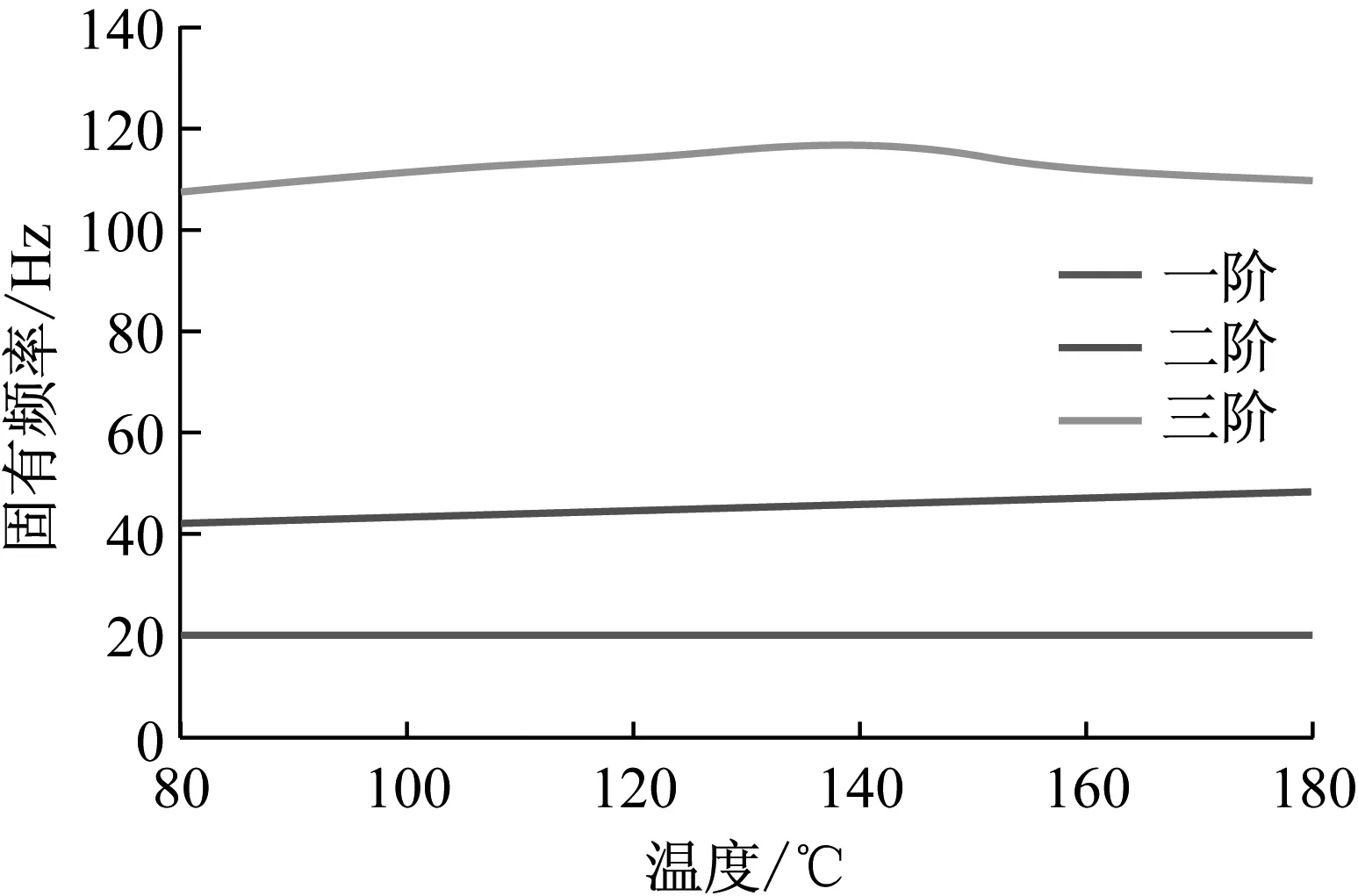
图6 模态频率变化曲线
4 复合材料层合板高温环境结构动力学建模
利用MSC Patran/Nastran建立目标结构的有限元模型,如图7所示。

图7 有限元模型
其中,使用四节点壳单元(QUAD4)作为板结构的单元,使用质量点单元来对传感器质量进行建模。边界条件方面,在对应约束边界处添加弹簧单元作为约束条件,从而满足在边界上的热应力情况。
材料属性上,首先使用二维各向异性材料建立单层板的材料属性,然后使用基于层合板理论的Laminate模块建立层合板材料,其中铺层形式按照TSM材料设计角度进行铺层,如图8所示。
热环境的建模方面,对板面整体施加均一的温度场。需要注意的是,由于是单边加热,所以板的两面温度并不一致。所以在建模过程中,需要考虑版中的温度梯度分布问题。故建立温度场时,采用了Element Variable类型建立对应的温度场。
模型建立完成后,使用MSC Nastran的SOL106非线性静力计算模块进行计算,此计算模块会首先计算其热应力场,然后形成对应的几何微分刚度阵添加到系统刚度阵中,最后计算高温环境下的结构模态频率及振型。得到的热应力场及前四阶振型,如图9所示。
5 高温环境结构参数灵敏度分析
先对常温环境下的参数灵敏度进行计算,得到结果如图11所示。
其中,parameter代表不同物理参数,response代表不同阶次的模态频率。这里的参数编号对应,见表1。


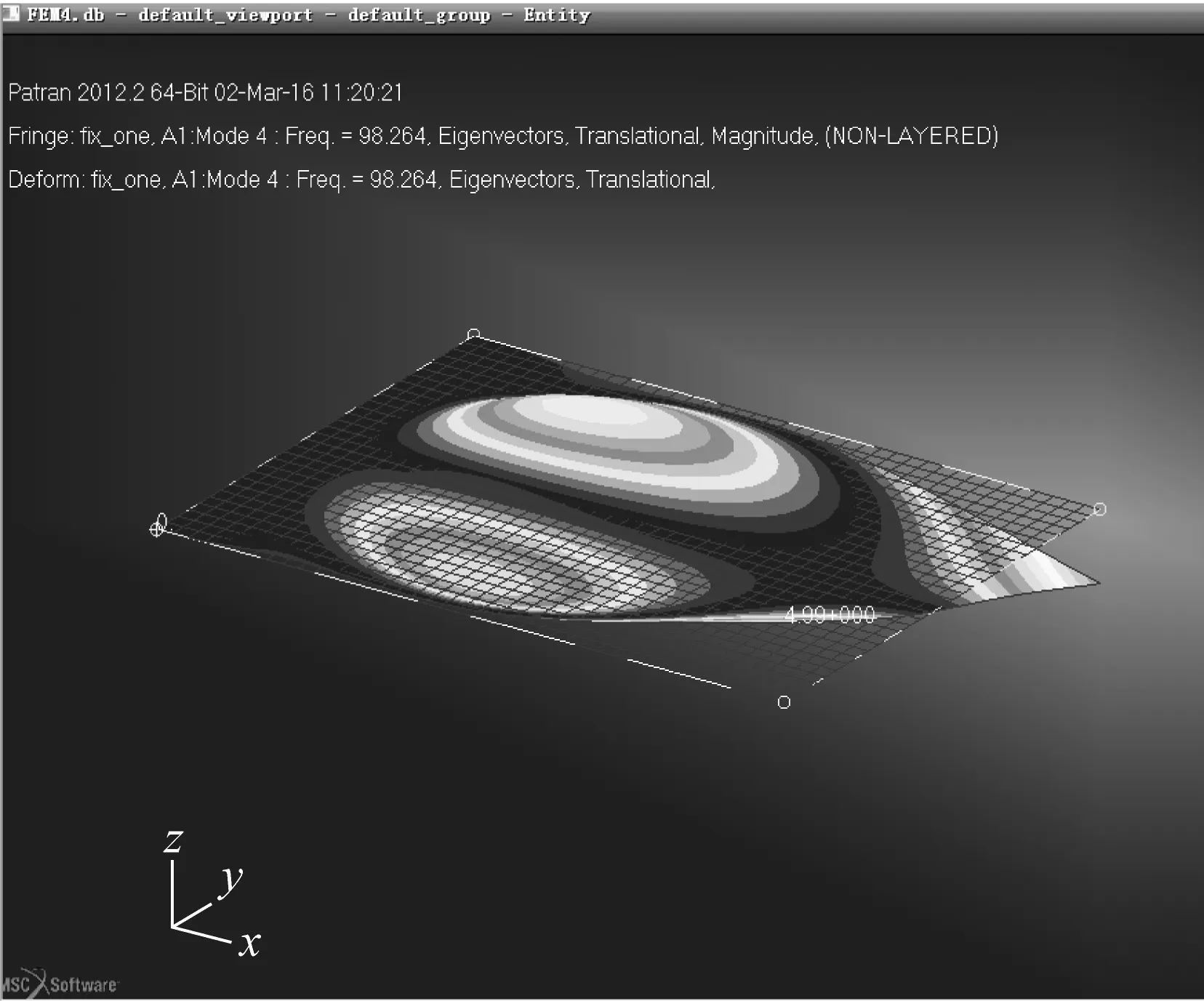
图10 前四阶模态振型(左上:一阶,右上:二阶,左下:三阶,右下:四阶)
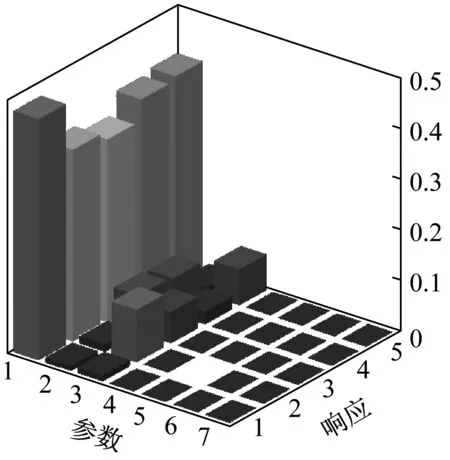
图11 常温环境灵敏度分析结果
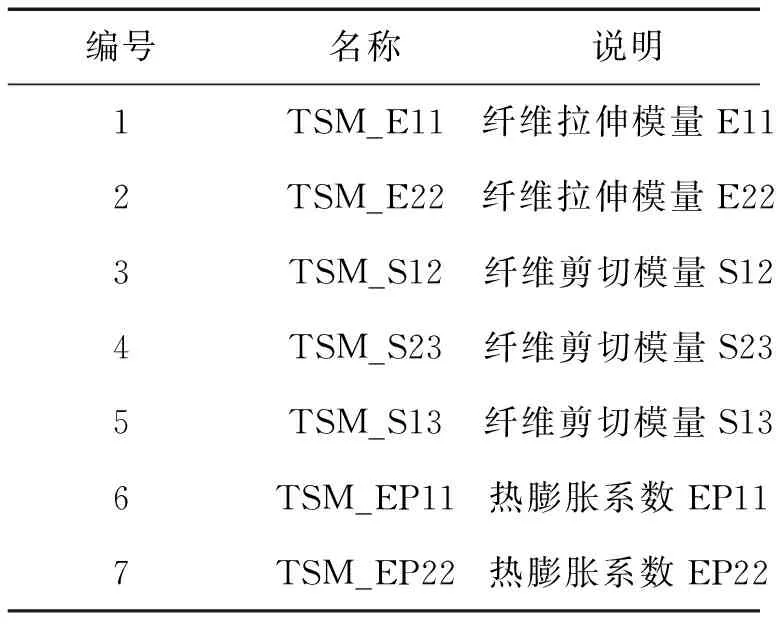
编号名称说明1TSM_E11纤维拉伸模量E112TSM_E22纤维拉伸模量E223TSM_S12纤维剪切模量S124TSM_S23纤维剪切模量S235TSM_S13纤维剪切模量S136TSM_EP11热膨胀系数EP117TSM_EP22热膨胀系数EP22
可以看到,在常温环境下热膨胀系数对固有频率的影响基本为0。而影响最大的为E11即沿着约束方向的拉伸模量。而对于高温环境,灵敏度分析的结果与传统的灵敏度分析有所区别。
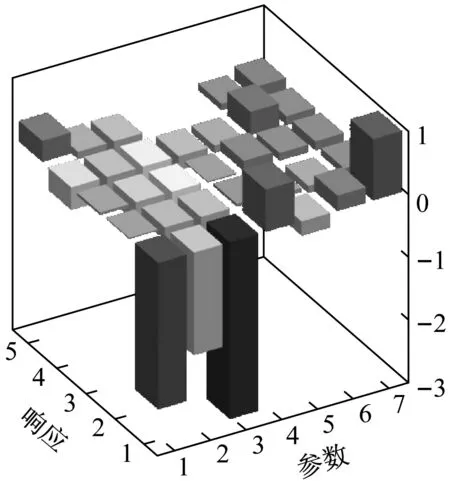
图12 高温环境灵敏度分析
可以看到,在高温环境下,各参数的影响发生了巨大的变化。本来灵敏度数值为正的弹性模量等参数变为负数,而热膨胀系数的影响逐渐加强,这是由于高温动力学问题本身的非线性特征所带来的。
随着温度的升高,各个参数呈现出非常复杂的变化规律,如图13所示。

图13 灵敏度随温度变化曲线(一阶固有频率)
根据本节的分析,所选择的各项参数均有着不同的物理意义,且对模型计算响应都有较大影响。其中,各向拉伸模量TSM_E11、TSM_E22和剪切模量TSM_S12 对于常温环境固有频率的影响较大。另一方面,随着温度的变化,这些弹性参数也会发生变化,这也将带来误差。而对于高温环境模态计算,热膨胀系数决定了热应力的计算结果,其对于高温环境模态计算结果的影响是非常重要的。而之前影响不大的TSM_S23、TSM_E13也体现出了影响。所以,在后续的模型修正工作中,将继续沿用本节灵敏度分析所使用的参数作为修正参数。
6 模型修正
在进行高温环境模型修正之前,首先对模型进行验证,利用试验得到的前三阶固有频率与有限元模型预示结果进行对比,情况如表2所示。

表2 常温环境下试验结果与有限元结果对比
可以看到结果对应良好,说明结构的常温物理参数以及边界条件建模准确。
然后,先根据之前的离散度计算公式(13),计算各阶固有频率测试结果离散度,并代入修正参数。从实验结果离散度的设置可以看出,二阶模态试验结果不确定性较低,故其在修正计算中的占比也较低。
另一方面,按照对各个参数的预估,设置修正参数的离散度。其中,拉伸模量E11在测量上本身比较准确,不确定性较小,故离散度设置较低。剪切模量S23与S13对响应的影响较小,为保证计算效果设置较低,其他参数离散度设置相对较高,使其在修正计算中的占比更高。离散度的设置相当于对参数和响应的加权处理,这种处理描述了各个未知量的不确定性,从而更加合理地描述实际物理情况。离散度设置情况如表3所示。
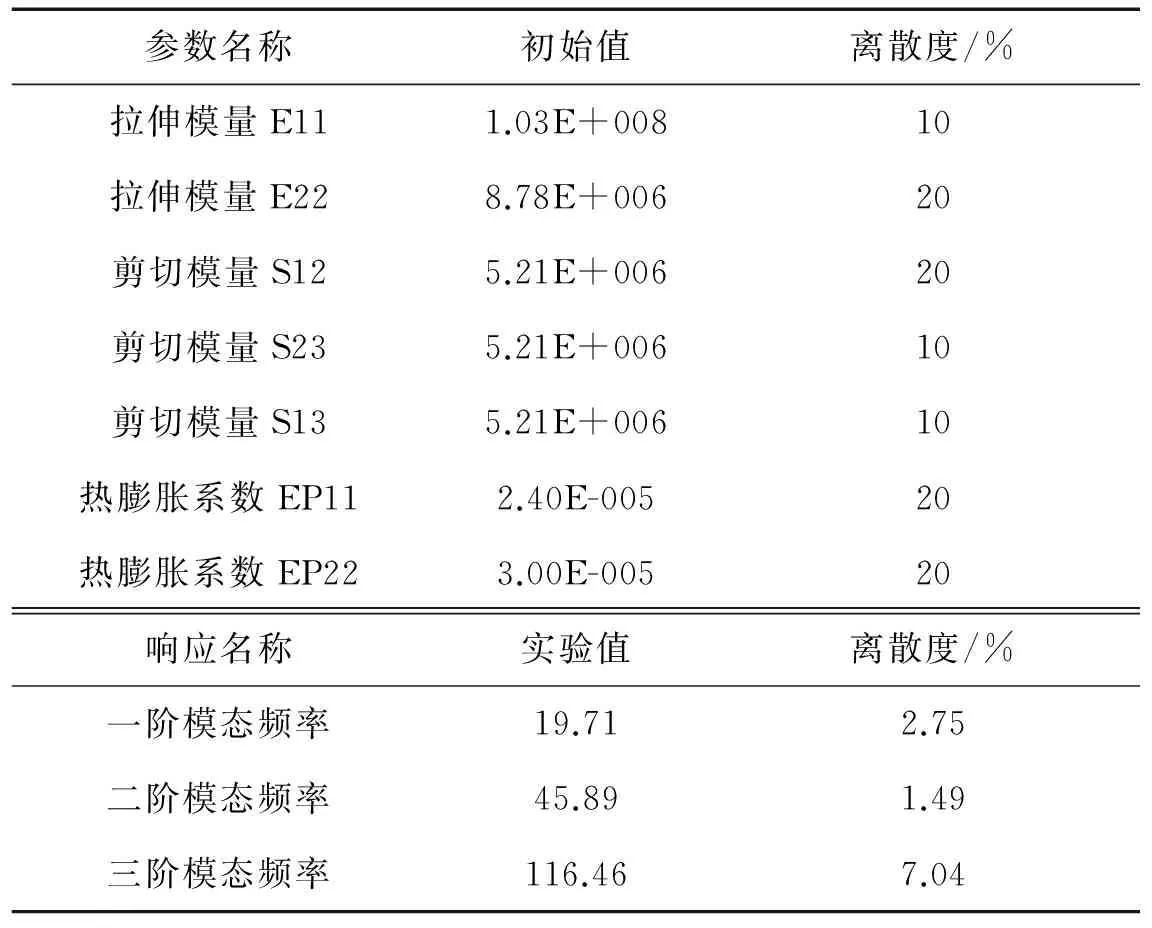
表3 参数及响应离散度设置
应用本研究设计的方法,利用FEMtools软件的二次开发功能编译自定义求解序列。分别对各个温度下的模型参数进行修正,以140℃为例,依然选择灵敏度分析时选择的七个参数作为修正参数。修正计算收敛准则采用前三阶计算固有频率与试验值之间误差的平均值作为收敛目标函数,当目标函数小于设定的标准时,迭代计算停止,修正完成。收敛曲线如图14所示。
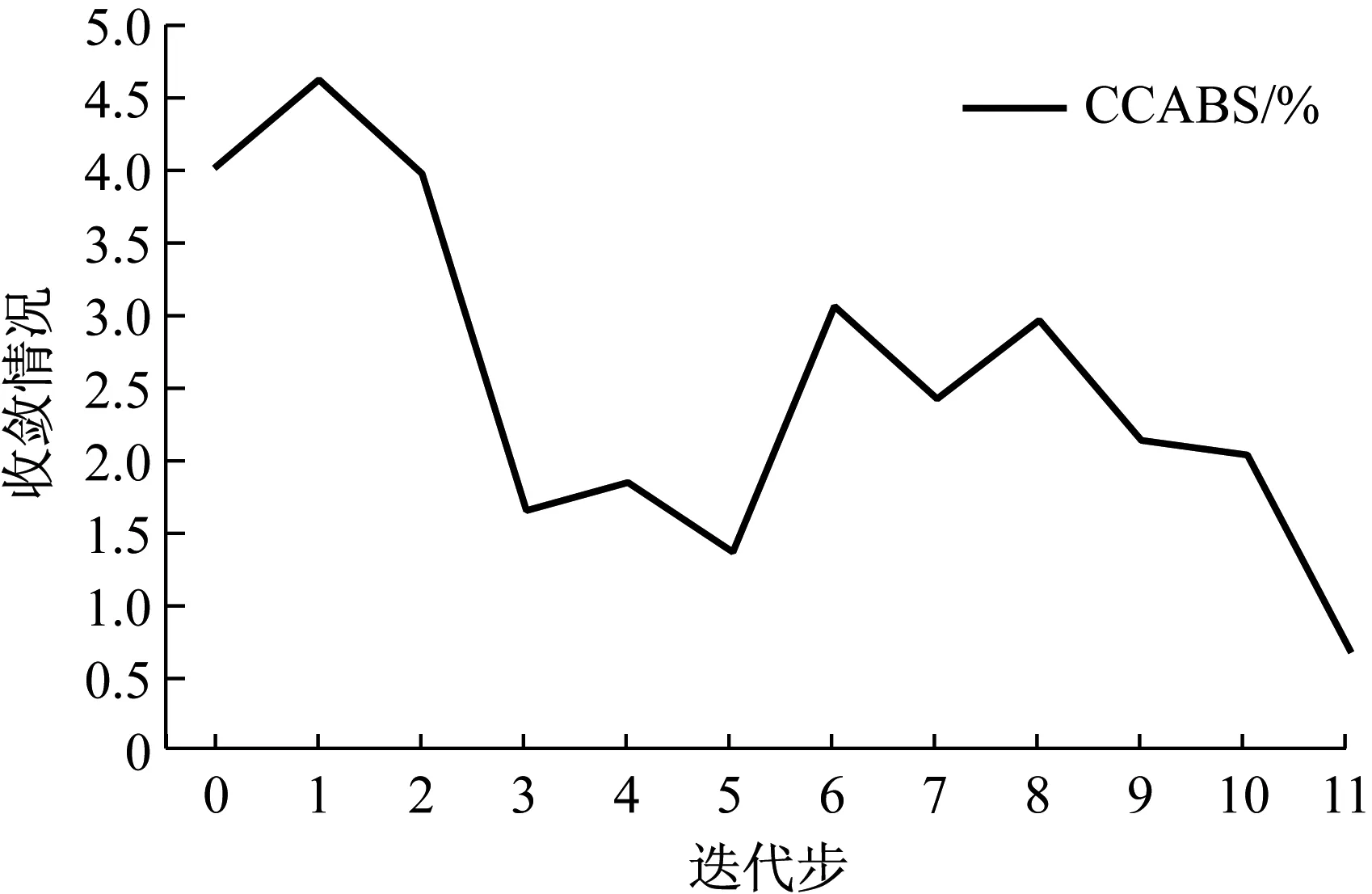
图14 修正计算收敛曲线
从收敛曲线的情况来看,虽然整体上达到了所设定的误差目标,计算结果也比较合理,但是收敛情况并不是非常理想的单一方向下降。这是由于问题的非线性导致的,想要解决这一问题还需要进一步研究适用于非线性问题的算法。目前的方法能够解决现有问题,但还有改进的空间。修正前后结果的对比情况,见表4和表5。
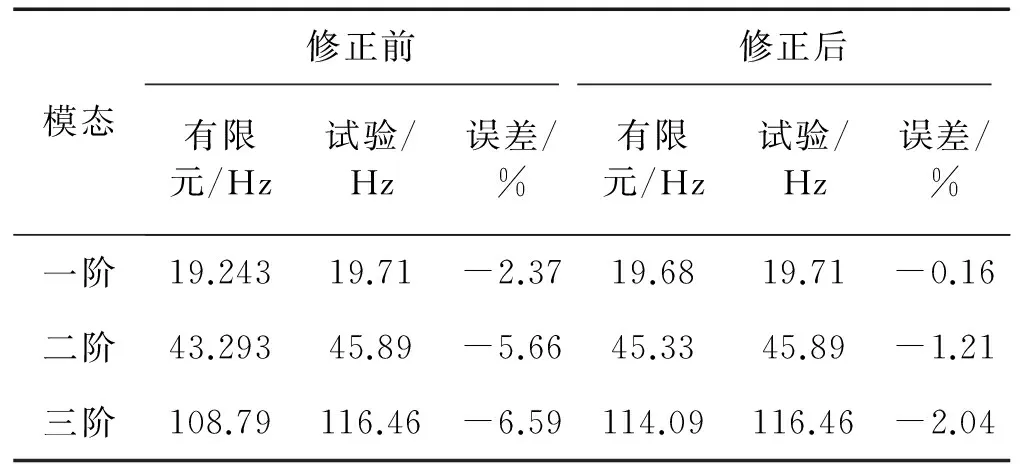
表4 修正前后结果对比情况(140 ℃)
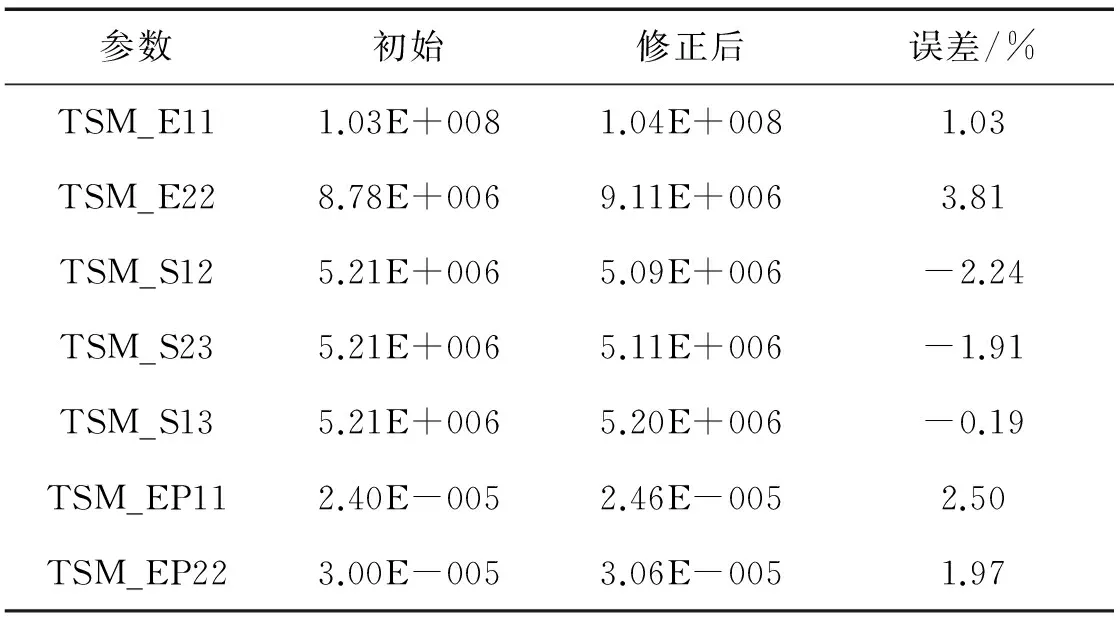
表5 修正前后参数对比(140 ℃)
可以看到,经过修正模态频率误差有了明显下降。同时,参数改变主要集中在弹性模量和热膨胀系数上。参数改变量合理,符合预期。
按照这种方式,对各个温度下的物理参数均进行修正,修正后各阶频率误差对比情况,如表6所示。
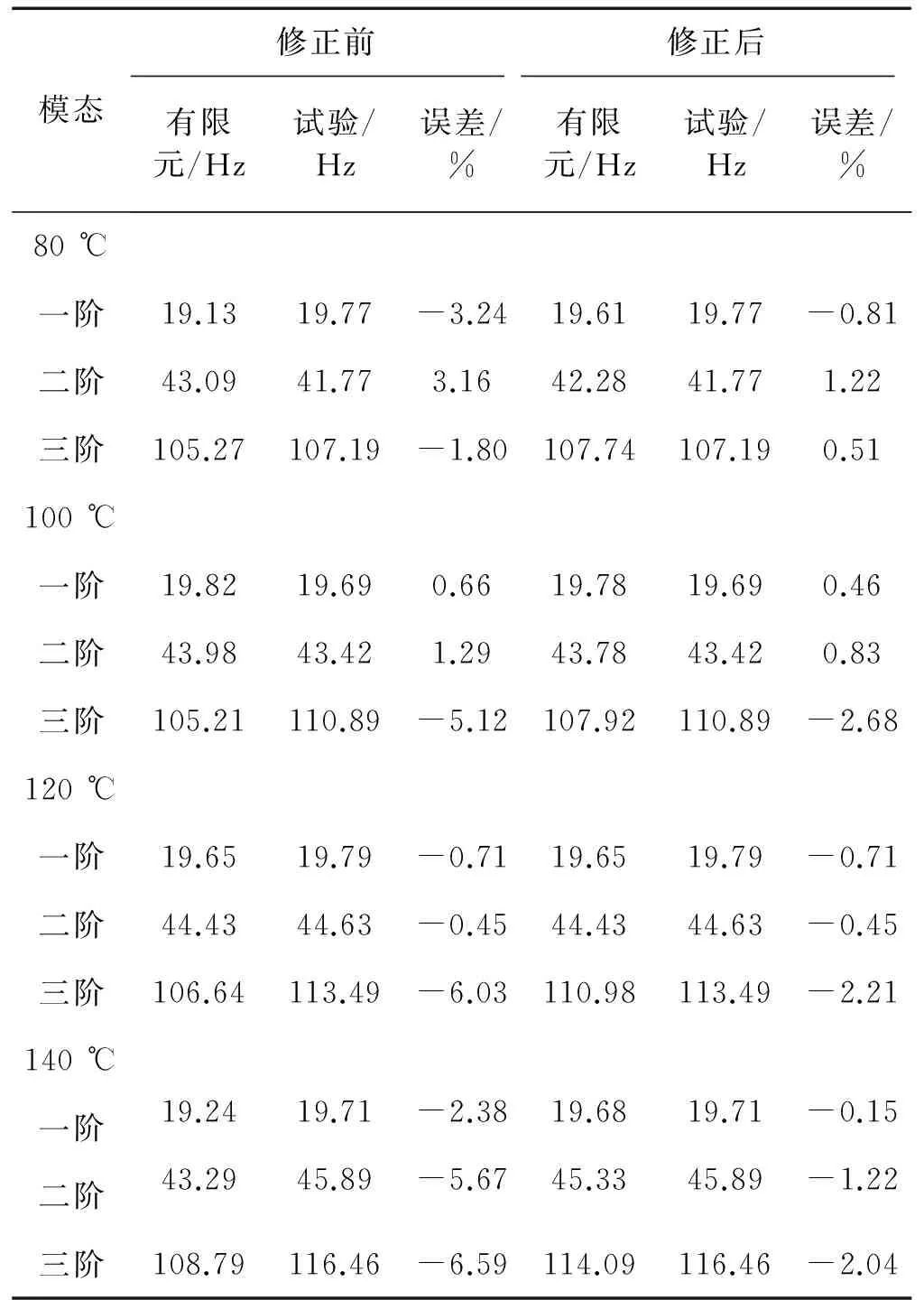
表6 修正前后误差对比
修正前后对应一阶、二阶固有频率的温度变化曲线,如图15~17所示。
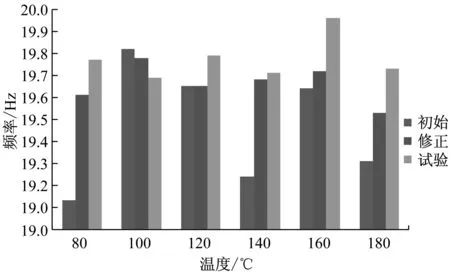
图15 温度-固有频率对比(一阶固有频率)
可以看到,经过修正各个温度下固有频率的对应情况均有所改善,误差最大控制在2.68%。修正结果合理,修正有效。
7 结 论
本文提出了一种新的基于贝叶斯参数估计的高温环境结构动力学模型修正方法。通过贝叶斯参数估计,可以将测试和参数的不确定性考虑入修正计算,从而更加准确地描述实际问题。利用本方法,对一复合材料层合板结构进行了模型修正研究,通过修正改善了在高温环境下模型的动力学特性预示结果。

图16 温度-固有频率对比(二阶固有频率)

图17 温度-固有频率对比(三阶固有频率)
本方法中一个重要的特征是需要设定响应和参数的离散度。其中,参数的离散度可以通过对参数的预估来设置。而对于响应的离散度,可以按照试验情况进行设置,或者按照离散度公式进行计算而得到。
在本研究中,进行了高温环境下复合材料结构的动力学试验。得到的结果基本合理,温度与固有频率之间呈现线性对应关系。但是,这类试验有很多需要注意的地方,包括试件的夹持与安装需要符合对应的工艺,高温环境下部分模态会出现混叠现象等。
相对于传统各项同性材料,复合材料在高温环境下有着更加复杂的特性。从灵敏度分析可以看到,参数灵敏度和温度之间呈现非线性的对应关系。这代表参数和高温动态响应之间也呈现一种非线性的关系。这对参数的设置和迭代计算的过程提出了更高的要求。在后续的研究中,可以考虑通过智能优化算法来提升修正运算的计算性能。
[1] THORNTON E A. Thermal structures-four decades of progress[J]. J. Aircr, 1992, 29(3):485-498.
[2] THORNTON E A. Thermal structures for aerospace applications[J]. AIAA, Reston, VA, 1996(2):153:161.
[3] 杨亚政,杨嘉陵,方岱宁. 高超声速飞行器热防护材料与结构的研究进展[J]. 应用数学和力学,2008(1):47-56.
YANG Yazheng, YANG Jialing, FANG Daining. Research progress on the thermal protection materials and structures in hypersonic vehicles[J]. Applied Mathematics and Mechanics, 2008(1):47-56.
[4] 孟松鹤, 杜善义, 韩杰才. 热防护系统及材料的研究进展[C]//复合材料——基础, 创新, 高效: 第十四届全国复合材料学术会议论文集 (上). 2006.
[5] 苏芳, 孟宪红. 三种典型热防护系统发展概况[J]. 飞航导弹, 2006(10): 57-60.
SU Fang, MENG Xianhong. Research progress on three classical thermal protection systems[J]. Winged Missiles Journal, 2006(10): 57-60.
[6] 郭朝邦,李文杰. 高超声速飞行器结构材料与热防护系统[J]. 工艺与材料, 2010(4):88-94.
GUO Chaobang, LI Wenjie. A research on structural materials and thermal protection systems of hypersonic vehicles[J]. Processing and Materials, 2010(4):88-94.
[7] 夏德顺.重复运载器金属热防护系统的评述[J].导弹与航天运载技术,2002(2):21-26.
XIA Deshun. A review on thermal protection systems for reusable vehicles[J]. Missiles and Astronautical Technology, 2002(2):21-26.
[8] BAILEY C D. Vibration of thermally stressed plates with various boundary conditions[J]. Am. Inst. Aeronaut. Astronaut, 1973,11(1):14-19.
[9] CHANG W P, SHOOU-CHIAN J. Nonlinear free vibration of heated orthotropic rectangular plates[J]. Int. J. Solids Struct., 1986, 22(3):267-281.
[10] CHANG W P, WAN S M. Thermomechanically coupled non-linear vibration of plates[J]. Int. J. Non-Linear Mecha. 1986, 21(5):375-389.
[11] BROWN A M. Temperature-dependent modal test/analysis correlation of X-34 FASTRAC composite rocket nozzle[J]. J. Propuls. Power, 2002, 18(2):284-288.
[12] 刘芹, 任建亭, 姜节胜, 等. 复合材料层合板非线性热振动分析[J]. 动力学与控制学报, 2005, 3(1): 78-83.
LIU Qin, REN Jianting, JIANG Jiesheng, et al. Nonlinear thermal vibration characteristic analysis composite laminated plates[J]. Journal of Dynamics and Control, 2005, 3(1): 78-83.
[13] 刘芹, 任建亭, 姜节胜, 等. 复合材料薄壁圆柱壳热振动特性分析[J]. 机械强度, 2006, 28(5): 643-648.
LIU Qin, REN Jianting, JIANG Jiesheng, et al. Nonlinear thermal vibration characteristic analysis of composite thin-cylindrical shells[J]. Journal of Mechanical Strength, 2006, 28(5): 643-648.
[14] DANTAS L B, ORLANDE H R B. A function estimation approach for determining temperature-dependent thermo-physical properties[J]. Inverse Probl. Eng., 1996, 3(4): 261-279.
[15] YANG C. Determination of the temperature dependent thermophysical properties from temperature responses measured at medium’s boundaries[J]. Int.J. Heat Mass Transf, 2000, 43(7): 1261-1270.
[16] LIU C. An efficient simultaneous estimation of temperature-dependent thermophysical properties[M]. CMC-Tech science press, 2006, 77.
[17] CZÉL B, GRF G. Simultaneous identification of temperature-dependent thermal properties via enhanced genetic algorithm[J]. Int. J. Thermophys, 2012, 33(6): 1023-1041.
[19] MAHNKEN R. An inverse finite-element algorithm for parameter identification of thermoelastic damage models[J]. Int. J. Numer. Methods Eng., 2000, 48(7): 1015-1036.
[20] MERAGHNI F, CHEMISKY Y, PIOTROWSKI B, et al. Parameter identification of a thermodynamic model for superelastic shape memory alloys using analytical calculation of the sensitivity matrix, Eur[J]. J. Mech. -A/Solids, 2014, 45: 226-237.
[21] POTTIER T, TOUSSAINT F, LOUCHE H, et al. Inelastic heat fraction estimation from two successive mechanical and thermal analyses and full-field measurements[J]. Eur. J. Mechan.-A/Solids, 2013, 38: 1-11.
[22] 邢晶晶, 张能辉, 王明禄. 黏弹性薄板的热振动[J]. 振动与冲击, 2005, 24(5): 23-25.
XING Jingjing, ZHANG Nenghui, WANG Minglu. Thermal vibration of thin viscoelastic plates[J]. Journal of Vibration and Shock, 2015, 24(5): 23-25.
[23] 刘芹, 任建亭, 郭运强, 等. 埋入形状记忆合金丝的复合材料圆柱壳壁板的热振动特性分析[J]. 振动与冲击, 2007, 26(7): 18-21.
LIU Qin, REN Jianting, GUO Yunqiang, et al. Thermal vibration characteristics analysis of a composite thin-cylindrical panel embedded with shape memory alloy wires[J]. Journal of Vibration And Shock, 2007, 26(7): 18-21.
[24] MOTTERSHEAD J E, FRISWELL E. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration, 1993, 167(2): 347-375.
[25] MICHAEL F, MOTTERSHEAD J E. Finite element model updating in structural dynamics[M]. Springer, 1995,38.
[26] 姜东,费庆国,吴邵庆. 基于摄动法的不确定性有限元模型修正方法研究[J]. 计算力学学报,2014(4):431-437.
JIANG Dong, FEI Qingguo, WU Shaoqing. Perturbation based uncertain finite element model updating method[J]. Journal of Computational Mechanics, 2014(4):431-437.
[27] 方圣恩,林友勤,夏樟华. 考虑结构参数不确定性的随机模型修正方法[J]. 振动.测试与诊断,2014(5):832-837.
FANG Shengen, LIN Youqin, XIA Zhanghua. Stochastic model updating method for structural parameters considering uncertainty[J]. Journal of Vibration,Measurement & Diagnosis, 2014(5):832-837.
[28] 陈学前,杜强,冯加权. 基于结构参数不确定性的有限元模型修正[J]. 机械科学与技术,2007(8):965-968.
CHEN Xueqian, DU Qiang, FENG Jiaquan. Modification of Finite Element Model (FEM) considering the uncertainty of structural parameters[J]. Mechanical Science And Technology For Aerospace Engineering, 2007(8):965-968.
[29] 房长宇,张耀庭. 基于参数不确定性的预应力混凝土梁模型修正[J]. 华中科技大学学报(自然科学版),2011,11:87-91.
FANG Changyu, ZHANG Yaoting. Model updating of prestressed concrete beams using parameters uncertainty[J]. Journal of Huazhong University of Science And Technology Nature Science, 2011,11:87-91.
[30] 张秋虎. 考虑结构参数不确定性的有限元模型修正方法研究[D].合肥:合肥工业大学,2014.
[31] 姜东,费庆国,吴邵庆. 基于区间分析的不确定性结构动力学模型修正方法[J]. 振动工程学报,2015(3):352-358.
JIANG Dong, FEI Qingguo, WU Shaoqing. Updating of structural dynamics model with uncertainty based on interval analysis[J]. Journal of Vibration Engineering, 2015(3):352-358.
[32] 何成,陈国平,何欢. 径向基模型的不确定性模型区间修正与确认[J]. 机械工程学报,2013,11:128-134.
HE Cheng, CHEN Guoping, HE Huan. Interval model updating and validation with uncertainty based on the radial basis function[J]. Journal of Mechanical Engineering, 2013,11:128-134.
[33] 张建新. 基于贝叶斯方法的有限元模型修正研究[D].重庆:重庆大学,2014.
[34] 韩芳,钟冬望,汪君. 基于贝叶斯法的复杂有限元模型修正研究[J]. 振动与冲击,2012,31(1):39-43.
HAN Fang, ZHONG Dongwang, WANG Jun. Complicated finite element model updating based on Bayesian method[J]. Journal of Vibration and Shock, 2012,31(1):39-43.
[35] 张明亮. 基于贝叶斯理论的材料非线性桥梁结构模型修正与损伤识别[D].长春:吉林大学,2011.
[36] 万华平,任伟新,黄天立. 基于贝叶斯推理的随机模型修正方法[J]. 中国公路学报,2016(4):67-76.
WAN Huaping, REN Weixin, HUANG Tianli. Stochastic model updating approach by using bayesian inference[J]. China Journal of Highway and Transport, 2016(4):67-76.
[37] HUMBERT L, THOUVEREZ F, JÉZÉQUEL L. Finite element dynamic model updating using modal thermoelastic fields[J]. Journal of Sound and Vibration, 1999, 228(2): 397-420.
[38] HE C, CHEN G, HE H, et al. Model updating of a dynamic system in a high-temperature environment based on a hierarchical method[J]. Finite Elements in Analysis and Design, 2013, 77: 59-68.
[39] 何成. 高温环境下结构动力学建模关键技术研究[D].南京:南京航空航天大学,2014.
[40] SUN Kaipeng, ZHAO Yonghui, HU Haiyan. Identification of temperature-dependent thermal-structural properties via finite element model updating and selection[J]. Mechanical Systems and Signal Processing, 2015, 52: 147-161.
[41] 张保强. 热结构不确定性动力学仿真及模型确认方法研究[D].南京:南京航空航天大学,2012.
Structural dynamic model updating under high temperature environment
YUAN Zhaoxu, YU Kaiping
(School of Aeronautics, Harbin Institute of Technology, Harbin 150001, China)
A new Bayesian parametric estimation-based model updating method for structures under high temperature environment (HTE) was proposed here. It was used to update the dynamic model of an actual composite laminate structure. The main idea of this method was to update the FE model of a structure with its modal frequencies test data under HTE. The feature of this method was using the dispersion of parameters and responses to describe their uncertainty and then to solve actual problems more reasonably. The dynamic tests of the composite structure were conducted under HTE to obtain its modal frequencies under HTE. The test data were used to update the FE model of the composite structure. Before updating, a sensitivity analysis was performed for the model to explore relations among its parameters and the structure’s dynamic responses. Test data and pre-estimations of parameters to be updated were used to set up their dispersions. Finally, the updating computation was done with a self-programmed algorithm. After updating, the relations among temperature and modal frequencies of the model were improved obviously to verify the effectiveness of the proposed method and its applicability for actual engineering problems.
structural dynamics under high temperature environment; model updating; composite material; sensitivity analysis
国家自然科学基金(11172078)
2016-03-08 修改稿收到日期:2016-06-28
袁昭旭 男,博士生,1988年生
于开平 男,博士,教授,1968年生
O327
A
10.13465/j.cnki.jvs.2017.15.026
