用于非线性动力分析的一种高效精细积分单步法
2017-08-30王海波李少毅
王海波, 陈 晋, 李少毅
(中南大学 土木工程学院,长沙 410075)
用于非线性动力分析的一种高效精细积分单步法
王海波, 陈 晋, 李少毅
(中南大学 土木工程学院,长沙 410075)
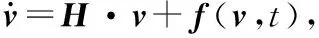
非线性动力方程;精细积分法;Romberg数值积分;龙格库塔法;单步法
传统数值积分方法,如中心差分法、Wilson法、Newmark法、Houbolt法等,在求解非线性动力方程中有着广泛的应用,但上述方法存在能量耗散及相位误差。基于上述原因,为更好满足工程实际的需求,求解非线性动力问题的高精度算法得到了发展。1994年前后,钟万勰等[1-2]提出精细积分方法,为非线性系统的时程分析开辟了崭新的途径。赵秋玲等[3-4]提出了一种非线性系统线性化的精细积分法,但计算结果精度不高;张洵安等[5]提出了一种精度较高的线性化迭代精细积分方法;裘春航等[6]将非线性部分用j次多项式来近似,然后借助于分段直接积分法进行求解,通过确定j值,可获得一系列具有不同精度的近似解,但需对状态矩阵求逆。
为避免对状态矩阵求逆,克服病态矩阵或逆矩阵不存在的缺点,张素英等[7]采用增维的方法,将非齐次动力方程化为齐次动力方程,然后假设各时间段状态矩阵为常矩阵,再利用精细积分求解;葛根等[8]对文献[7]进行了改进,提高了增维精细积分法的计算效率,但计算结果精度不高;李金桥等[9]先将非线性部分在tk时刻展开成泰勒级数形式,然后将非线性积分项泰勒展开法或高斯-勒让德数值积分法与精细积分法结合进行求解,一定程度上提高了计算结果的精度;任传波等[10]提出了一种不论是线性激励还是非线性激励都具有较高求解速度和精度的计算格式,但仅讨论了线性动力系统;向宇等[11]提出了一种较高精度的齐次扩容精细积分法,但显著增加了计算量;王海波等[12]将精细积分法和Adams-Bashforth-Moulton多步法相结合,提出了一种高精度、高效率的精细积分多步法,但需要使用单步法计算表头;谭述君等[13]基于Duhamel项精细积分方法,构造了几种求解非线性微分方程的数值算法;江小燕等[14]根据Hamilton变作用定律构造时空有限元矩阵,并结合传递矩阵原理和精细积分思想提出了精细时空有限元方法;李炜华等[15]利用改进的欧拉法对状态未知量进行预估及校正,然后结合辛时间子域法对非线性方程进行求解。
本文将精细积分法和Romberg数值积分结合,对计算过程中待求的vk+j/m(j=1,2,…,m),利用当前时刻vk,通过二阶龙格库塔法进行预估,提出了一种避免状态矩阵求逆的高效精细积分单步法。数值算例验证了算法的有效性。
1 高效精细积分单步法
讨论非线性动力方程:

(1)
利用指数矩阵将其转化为如下同解积分方程:
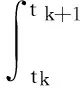
(2)
式中,vk+1、vk分别表示所求解向量在时刻tk+1和tk的值。
令
T=eHΔt
(3)
G(τ)=eH(tk+1-τ)f(v,τ)
(4)
式(2)变为:
vk+1=Tvk+v*(tk+1)
(5)
其中
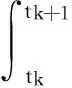
(6)
这样,将vk+1的表达式分解成了2项,第1项可直接采用精细积分精确得到,下面讨论第2项的数值求解方法。
本文采用Romberg积分对第2项进行数值直接积分。
由文献[10]可知,式(6)的Romberg积分格式为:
(7)
(j=1,2,…,m)(m=1,2,3,…)
其中
(8)
(9)
式(7)中,m的取值要视问题的求解精度而定,m取值越大精度越高。本文取m=2对式(6)进行计算,由式(4)、式(7)~式(9)可以得到如下计算步骤:

(10)
(11)
(12)
(13)
(14)
(15)
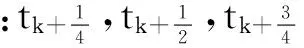

T1/2=T1/4·T1/4,T=T1/2·T1/2
(16)
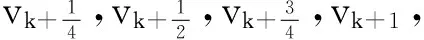

(17)
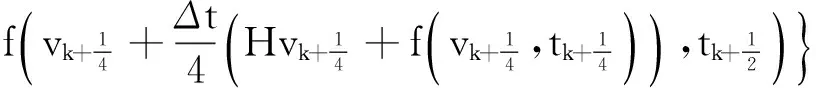
(18)
(19)
(20)
2 算例分析
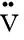
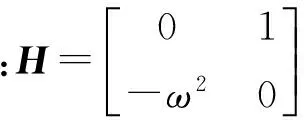
各种方法的前5 s分析结果及前40 s位移绝对误差(误差的绝对值,用R()表示,在下文中除另加说明外,误差均采用绝对误差表示)时程曲线分别见表1、图1。

表1 v1的数值结果比较(Δt=0.1 s)
从本例Δt=0.1 s计算结果(表1和图1)可知:本文单步法计算误差明显小于一次预-校法[12]和单步法1[6](按文献[6]中公式(23)计算),随着时间的增大,这种优势越来越明显。
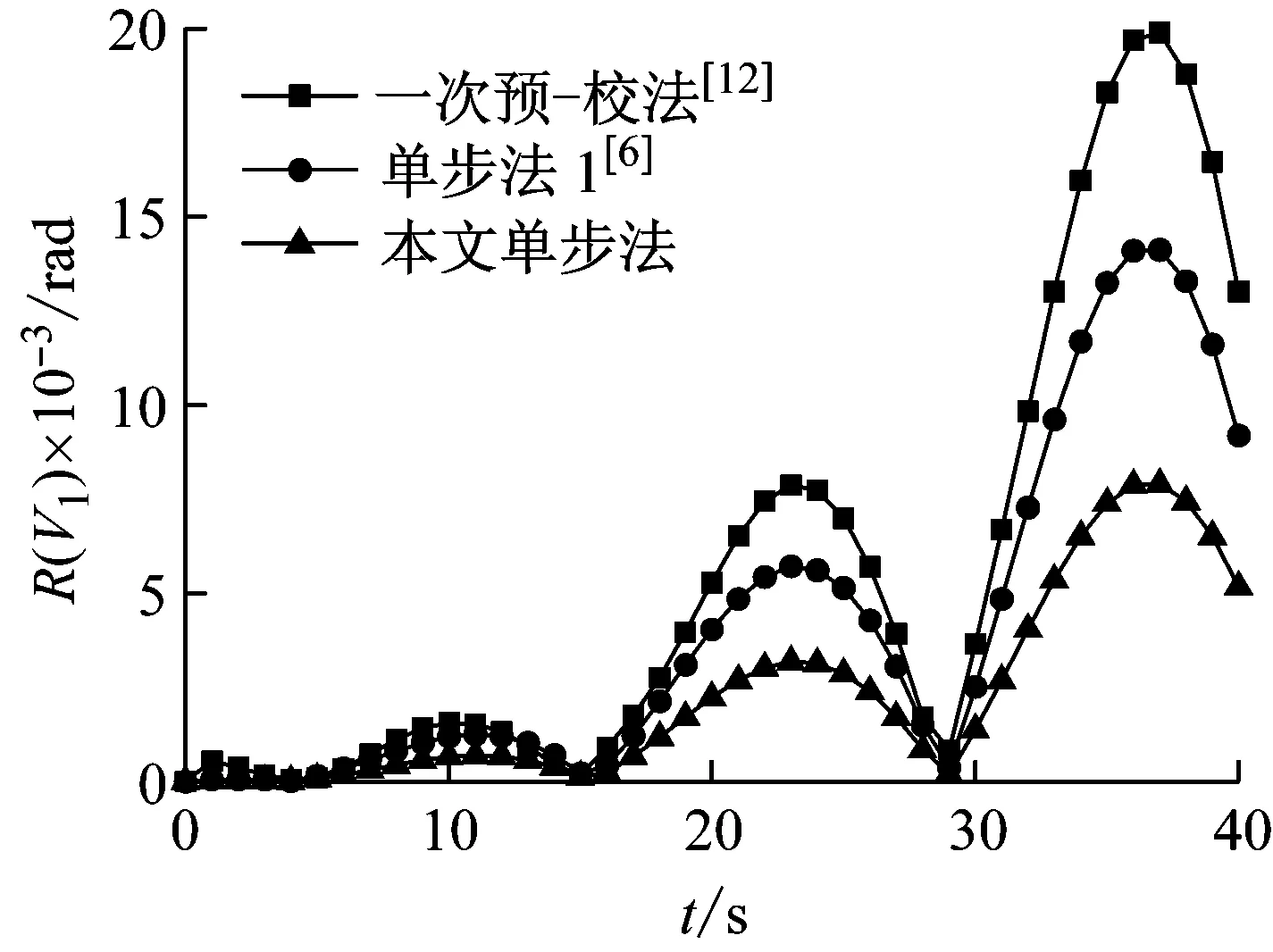
图1 三种方法解的误差R(v1)
算例2 考虑带参数a和b的Duffing方程[6]
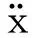
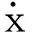
取初值v1(0)=0.3,v2(0)=0.5,采用Matlab编程计算,图2(a)、图2(b)分别给出了当线性阻尼系数a较小,b=2、b=45时,前20 s内3种方法的位移误差时程曲线(所取点为1 s的整数倍)。从图2中可知:随着激励幅值b的增加,本文单步法的误差有增加趋势,但误差值均较小;本文单步法与单步法2[6](按文献[6]中公式(16)计算)相比,误差稍大,但避免了状态矩阵求逆且无需对非齐次项进行求导运算,计算效率较高,两者计算时间比较见表2;本文单步法的误差明显小于一次预-校法[12],计算精度较高。

(a) a=0.3,b=2,Δt=0.2 s
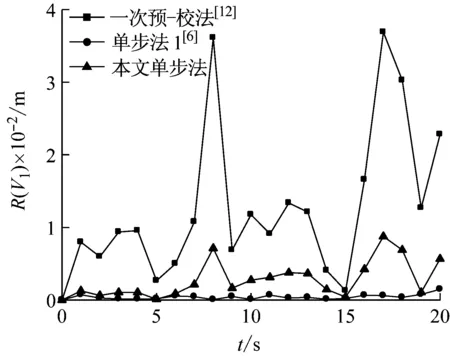
(b) a=0.3,b=45,Δt=0.05 s
表2 单步法2[6]与本文单步法计算时间比较
Tab.2 Comparisons of computation time for the single-step method 2 in Ref.[6]and proposed algorithm

时间步数执行10次的平均CPU时间/s单步法2[6]本文单步法1000.18410.132610000.60060.3744100003.81731.6770注:两种算法的计算条件:a=0.3,b=2,Δt=0.2s
以前述初值为起点,计算到200 s为止,轨迹线从100 s开始绘制,如图3所示。
由图3(a)和图3(b)可见,当暂态结束后,所有轨迹线都集中在一起,形成周期吸引子图形;而图3(c)则显示了轨迹线仍分散的混沌吸引子。一般地说,当线性阻尼系数a较小时,随着激励幅值b的增加,周期解可能分支为对称解,再经过一系列倍周期过程而进入混沌解。本例的收敛性和数值稳定性都较好,本文单步法在Δt=0.1 s和Δt=0.02 s算出的结果相近,对图3(a)的问题,即使采用步长Δt=0.5 s,本文单步法和单步法2[6]也能算出误差较小的结果,而一次预-校法[12]的结果已发散。
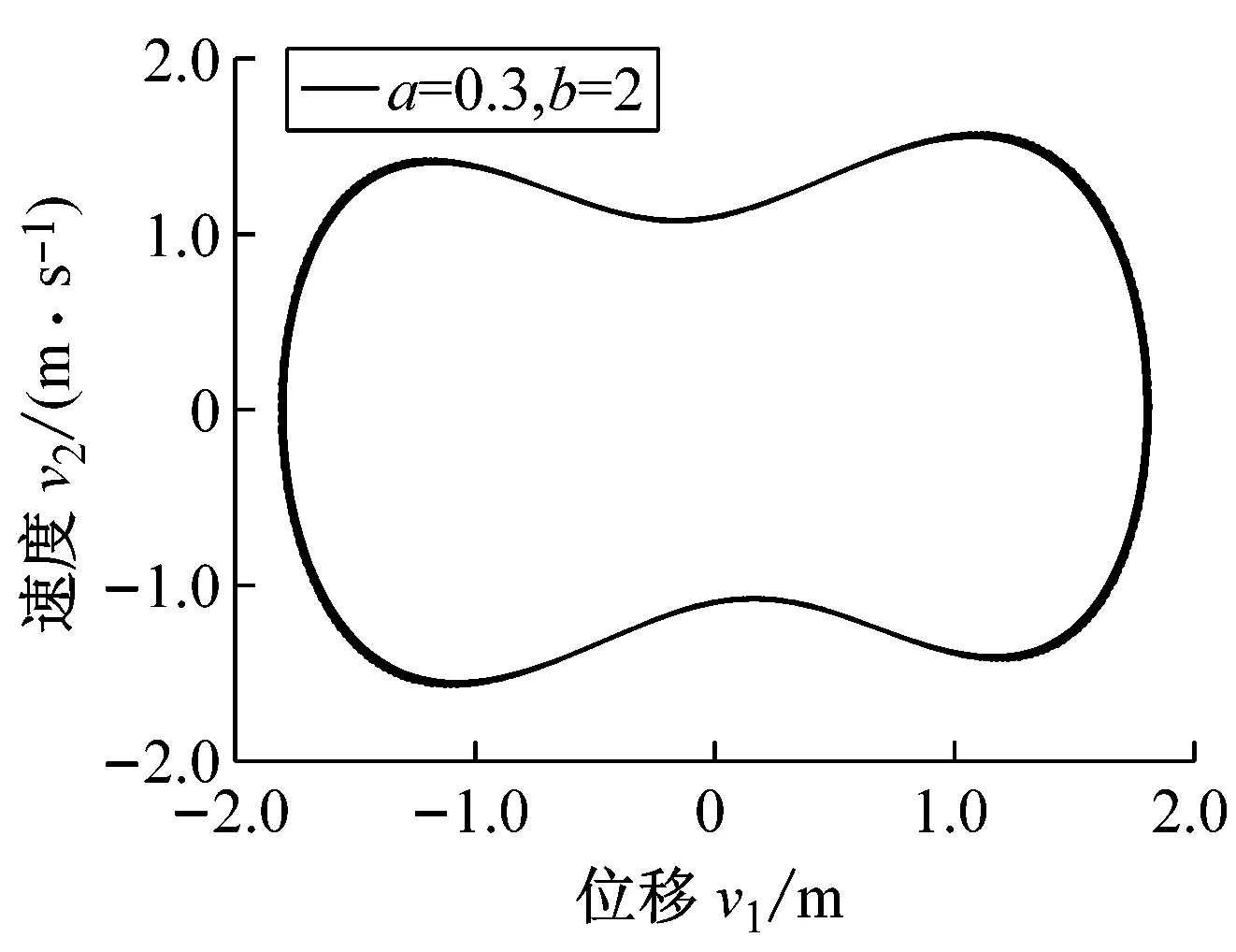
(a) a=0.3,b=2
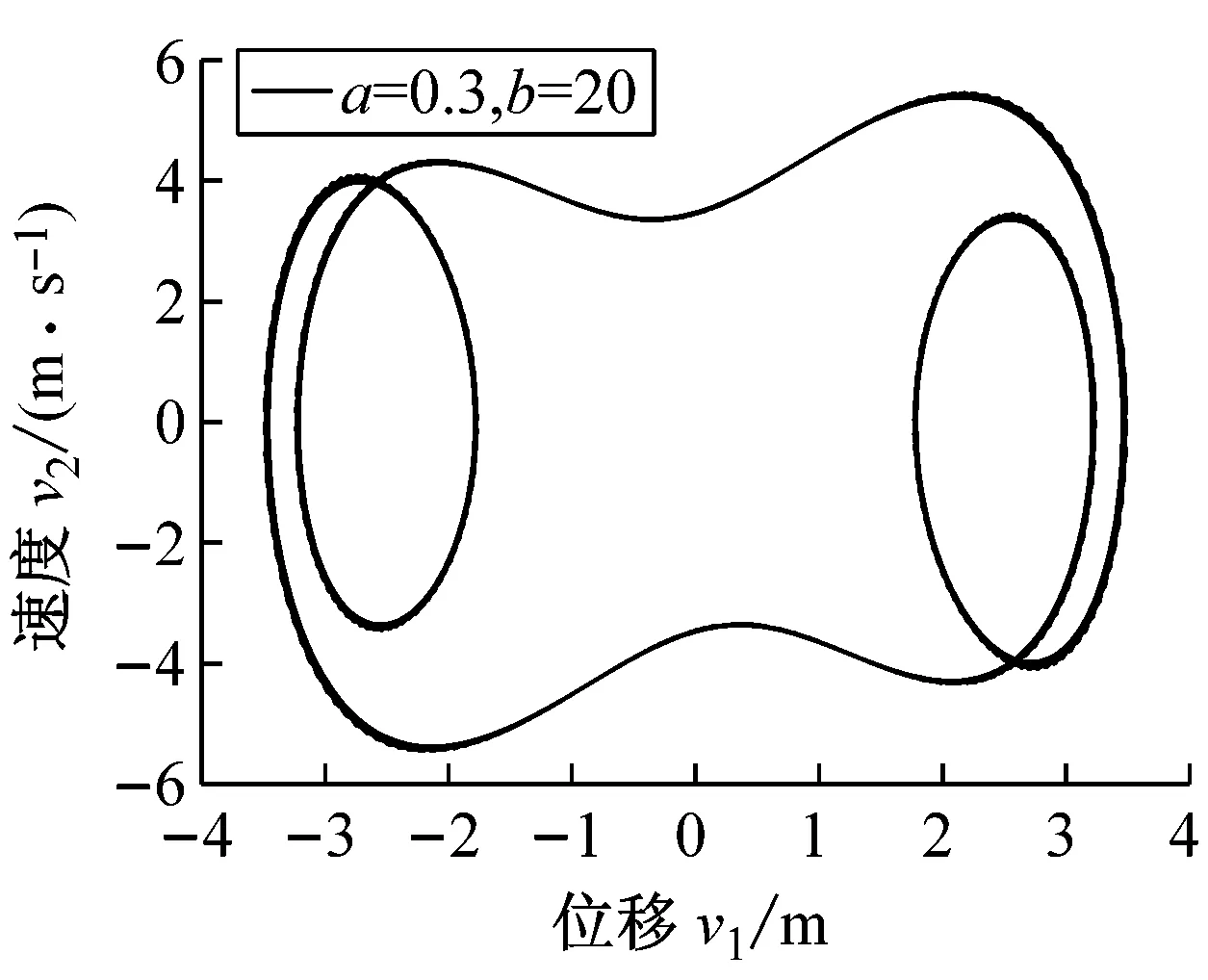
(b) a=0.3,b=20
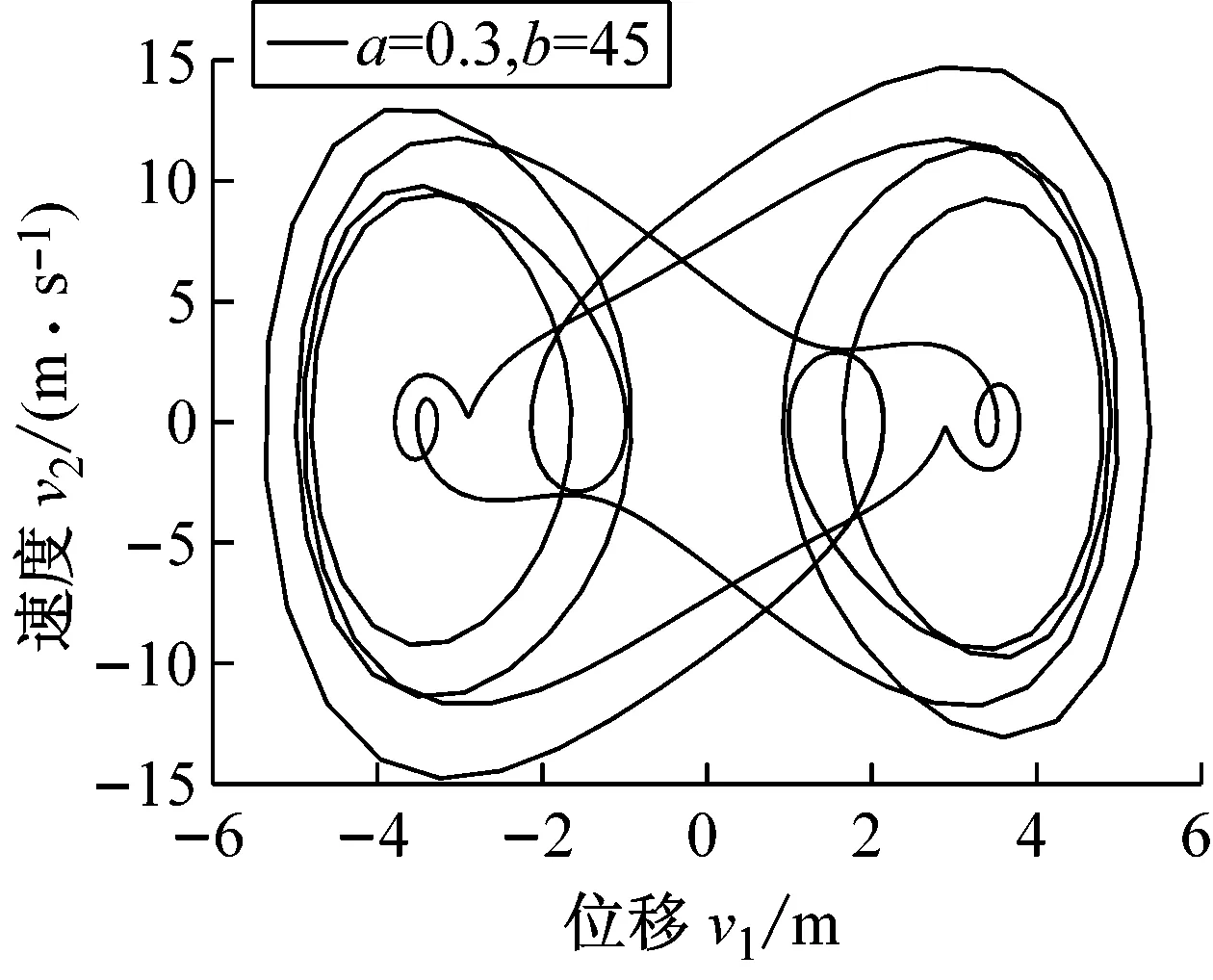
(c) a=0.3,b=45
算例3 受迫Van der Pol方程[15]为
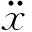
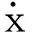
取α=1,β=0.2,ω=1.2,f=1.0,时间步长Δt=0.1 s,初始条件为:v1(0)=1.5,v2(0)=0.5,采用预估校正-辛时间子域法[15]及本文单步法,通过Matlab编程计算,前5 s分析结果及两种方法计算时间比较分别见表3、表4。从表3及表4可知:本文单步法与预估校正-辛时间子域法的计算结果均具有较高的精度,虽然前者精度略低于后者,但前者计算效率却远高于后者,且随着计算步数的增加,这种优势更加明显。

表3 v1的数值结果比较(Δt=0.1 s)
算例4 考虑平方非线性的二自由度动力学方程[8]
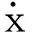
取初值v1(0)=v2(0)=0.1,v3(0)=v4(0)=0,本文单步法在时间步长Δt=0.1 s、0.5 s、1.0 s前15 s分析结果见表5。
表4 预估校正-辛时间子域法[15]与本文单步法计算时间比较
Tab.4 Comparisons of computation time for the predictor-corrector symplectic time-subdomain algorithm in Ref.[15] and the proposed algorithm

时间步数执行10次的平均CPU时间/s预估校正-辛时间子域法[15]本文单步法10013.75340.105220025.34020.149350059.79210.2109
由表5可知:随着时间步长的增大,本文单步法的精度逐渐降低;本文单步法在较大步长(Δt=1.0 s)情况下仍具有较理想的计算结果。
3 结 论

表5 v1、v2的数值结果比较
(2) 本文单步法是一种高精度、高效率和稳定性较好的方法。数值计算结果表明:取m=2时,本文单步法比单步法1[6]及一次预-校法[12]计算精度要高;与单步法2[6]、预估校正-辛时间子域法[15]相比,本文单步法在保持相同高精度计算结果的基础上,计算效率更高,在求解多自由度、强非线性动力响应问题中具有较大优势。
[1] 钟万勰. 结构动力方程的精细时程积分法[J]. 大连理工大学学报, 1994, 34(2): 131-136.
ZHONG Wanxie. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994, 34(2): 131-136.
[2] LIN Jiahao, SHEN Weiping, WILLIAMS F W. A high precision direct integration scheme for structures subjected to transient dynamic loading[J]. Computer & Structures, 1995, 6(1): 120-130.
[3] 赵秋玲. 非线性动力学方程的精细积分法[J]. 力学与实践, 1998, 20(6): 24-26.
ZHAO Qiuling. An accurate integration method for solving nonlinear dynamic problems[J]. Mechanics in Engineering, 1998, 20(6):24-26.
[4] 吕和祥,蔡志勤,裘春航. 非线性动力问题的一个显式精细积分算法[J]. 应用力学学报, 2001, 18(2): 34-40.
LÜ Hexiang, CAI Zhiqin, QIU Chunhang. An explicit precise integration algorithm for nonlinear dynamics problems[J]. Chinese Journal of Applied Mechanics, 2001, 18(2): 34-40.
[5] 张洵安,姜节胜. 结构非线性动力方程的精细积分算法[J]. 应用力学学报, 2000, 17(4): 164-168.
ZHANG Xunan, JIANG Jiesheng. The precise integration algorithm for nonlinear dynamics equations of structures[J]. Chinese Journal of Applied Mechanics, 2000, 17(4): 164-168.
[6] 裘春航,吕和祥,钟万勰. 求解非线性动力学方程的分段直接积分法[J]. 力学学报, 2002, 34(3): 369-378.
QIU Chunhang, LÜ Hexiang, ZHONG Wanxie. On segmented-direct-integration method for nonlinear dynamics equations[J]. Acta Mechanica Sinica, 2002, 34(3): 369-378.
[7] 张素英,邓子辰. 非线性动力方程的增维精细积分法[J]. 计算力学学报, 2003, 20(4): 423-426.
ZHANG Suying, DENG Zichen. Incremental-dimensional precise integration method for nonlinear dynamic equation[J]. Chinese Journal of Computational Mechanics, 2003, 20(4): 423-426.
[8] 葛根,王洪礼,谭建国. 多自由度非线性动力方程的改进增维精细积分法[J]. 天津大学学报, 2009, 42(2): 113-117.
GE Gen, WANG Hongli, TAN Jianguo. Improved increment-dimensional precise integration method for the nonlinear dynamic equation with multi-degree-of-freedom[J]. Journal of Tianjin University, 2009, 42(2): 113-117.
[9] 李金桥,于建华. 非线性动力方程避免状态矩阵求逆的级数解[J]. 四川大学学报(工程科学版), 2004, 36(4): 26-30.
LI Jinqiao, YU Jianhua. Series solution of nonlinear dynamics equations avoiding calculating the inversion of the state matrix[J]. Journal of Sichuan University(Engineering Science Edition), 2004, 36(4): 26-30.
[10] 任传波,贺光宗,李忠芳. 结构动力学精细积分的一种高精度通用计算格式[J]. 机械科学与技术, 2005, 24(12): 1507-1509.
REN Chuanbo, HE Guangzong, LI Zhongfang. A high precision and general computational scheme in precise integration of structural dynamics[J]. Mechanical Science and Technology, 2005, 24(12): 1507-1509.
[11] 向宇,黄玉盈,袁丽芸,等. 非线性系统控制方程的齐次扩容精细积分法[J]. 振动与冲击, 2007, 26(12): 40-44.
XIANG Yu, HUANG Yuying, YUAN Liyun,et al. Extended homogeneous capacity high precision integration method for control equation of nonlinear systems[J]. Journal of Vibration and Shock, 2007, 26(12): 40-44.
[12] 王海波,余志武,陈伯望. 非线性动力分析避免状态矩阵求逆的精细积分多步法[J]. 振动与冲击, 2008, 27(4): 105-108.
WANG Haibo, YU Zhiwu, CHEN Bowang. Precise integration multi-step method for nonlinear dynamic equations to avoid calculating inverse of state matrix[J]. Journal of Vibration and Shock, 2008, 27(4): 105-108.
[13] 谭述君,高强,钟万勰. Duhamel项的精细积分方法在非线性微分方程数值求解中的应用[J]. 计算力学学报, 2010, 27 (5): 752-758.
TAN Shujun, GAO Qiang, ZHONG Wanxie. Applications of Duhamel term’s precise integration method in solving nonlinear differential equtions[J]. Chinese Journal of Computational Mechanics, 2010,27(5):752-758.
[14] 江小燕,王建国. 非线性动力方程的精细时空有限元方法[J]. 工程力学, 2014, 31(1): 23-28.
JIANG Xiaoyan, WANG Jianguo. The precise space-time finite element method for nonlinear dynamic equation[J]. Engineering Mechanics, 2014, 31(1): 23-28.
[15] 李炜华,王堉,罗恩. 求解非线性结构动力方程的预估校正-辛时间子域法[J]. 计算力学学报, 2014, 31(4): 453-458.
LI Weihua, WANG Yu, LUO En. Predictor-corrector symplectic time-subdomain algorithm for nonlinear dynamic equations[J]. Chinese Journal of Computational Mechanics, 2014, 31(4): 453-458.
An efficient precise integration single-step method for nonlinear dynamic analysis
WANG Haibo, CHEN Jin, LI Shaoyi
(College of Civil Engineering, Central South University, Changsha 410075, China)
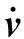
nonlinear dynamic equations; precise integration method; Romberg numerical integration; Runge-Kutta method; single-step method
国家自然科学基金(50908230)
2016-03-14 修改稿收到日期:2016-06-15
王海波 男,博士,副教授,1974年4月生
陈晋 男,硕士生,1993年7月生
O322; TU311.3
A
10.13465/j.cnki.jvs.2017.15.024
