一种基于声阵列信息融合及改进EEMD的信号降噪方法
2017-08-30顾晓辉
邸 忆, 顾晓辉, 龙 飞
(1. 南京理工大学 机械工程学院, 南京 210094;2. 贵州大学 智能信息处理研究所, 贵阳 550025)
一种基于声阵列信息融合及改进EEMD的信号降噪方法
邸 忆1, 顾晓辉1, 龙 飞2
(1. 南京理工大学 机械工程学院, 南京 210094;2. 贵州大学 智能信息处理研究所, 贵阳 550025)
针对声阵列多通道信号的去噪问题,提出一种基于多传声器信息融合辅助的改进总体平均经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)的被动声信号去噪方法。对标准EEMD进行改进,通过多通道信号频谱分析,选取多传声器信号最小有效频率作为各通道信号EEMD分解的筛选截止频率,采用改进的EEMD算法将原始信号快速分解为完备的IMF分量,有效抑制了模态混叠现象并提高信号分解效率;引入声阵列时延矢量封闭准则(Time Delay Vector Close Rule, TDVCR)概念,结合多传声器数据一致性融合及信号相关性理论,对各IMF分量进行相应的权重计算,再由已确定权值对各IMF分量进行加权重构得到去噪信号;最终通过半实物仿真试验以及同传统EMD去噪的比较验证了该算法在多通道信号去噪中的有效性和实用性。
声阵列;信号去噪;总体平均经验模态分解;数据一致性融合;时延矢量封闭准则
在现代战争中,声传感器阵列以其被动式探测、全天候工作和探测性能良好的优势被广泛应于反直升机地雷、防坦克智能雷、BAT子弹药等武器装备中[1]。随着信息化战争的发展,战场信号复杂化对声目标探测提出了更高的要求,信号预处理作为目标识别及跟踪的重要步骤之一,是优化目标识别效果,提升目标跟踪精度的前提,因此,高效的信号去噪方法显得尤为重要。
战场声信号具有较强的随机性和非平稳性特点,采用传统去噪方法[2-3]能够在一定程度上抑制噪声,但对包含尖峰或突变的非平稳信号的降噪性能有较大局限性。小波去噪[4-5]克服传统去噪方法的弱点,能够有效处理非平稳信号的噪声,然而小波去噪方法无法摆脱小波基选择及小波系数的复杂计算。Huang等[6]提出的经验模态分解(Empirical Mode Decomposition,EMD)同样能够较好地处理非平稳信号,而且无需考虑基函数选择,可以根据信号自身特点自适应地分解不同尺度的本征模态函数(Intrinsic Mode Function,IMF),因而被广泛应用于战场声目标探测[7]、地震信号降噪[8-9]、机械故障诊断[10]等领域。但是由于实测信号的非平稳性和复杂性,传统EMD信号分解常伴随着模态混叠现象,该现象会在信号去噪中引入不合理的信号分量,从而影响信号降噪效果,甚至造成降噪失效。国内外学者针对模态混叠现象提出了一些卓有成效的改进方法[11-14],其中最有效的方法是Wu提出的集合平均经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)算法。然而随后的研究[15-17]发现,EEMD在信号分解过程中引入白噪声,再通过传统EMD进行循环分解,这样虽抑制了模态混叠效应,但白噪声的引入会降低信号分解效率,产生“过分解”,甚至在原有IMF分量中带入虚假成分,那么,在使用EEMD进行信号去噪时需要先考虑算法本身的“过分解”和“虚假分解”问题,提高信号分解的效率和可靠性。
目前,大部分信号去噪方法主要以单传感器信号为处理对象,而针对阵列信号或多通道信号的去噪方法相对较少,文献[18]提出了一种多传声器小波多尺度信息融合的去噪方法,定义了声阵列信号的时延矢量封闭性,将多传感器信息融合理论与小波去噪相结合,采用信号多尺度分解及重构方法实现了阵列信号的自适应去噪。本文针对声阵列对被动声信号的去噪问题,借鉴时延矢量封闭准则,结合声阵列数据一致性融合理论[19]及多通道信号相关性,改进已有的EEMD算法,提出一种基于多传声器信息融合及最小频率截止EEMD的多通道信号去噪方法,通过半实物仿真试验验证了该方法的有效性。
1 声阵列信息融合及时延矢量封闭性
1.1 声阵列数据一致性融合理论
声阵列是将多个传声器按照一定排列规则分布于探测空间,通过观察每两个传声器接收到相同目标声波的时间差来估算声目标的重要信息。多传声器信息融合技术是声阵列探测的关键技术之一,综合利用多传声器信息,通过各传声器之间的性能互补,克服单个传声器的局限性,进而提高阵列整体性能。然而在声阵列中部分传声器可能会因损坏或者外界干扰而造成信号失真,从而导致其测量数据无效,那么有必要通过多传声器数据融合算法对声阵列中的各传声器进行甄别,剔除失效器件,确定最优传声器组,确保各传声器具有良好的数据一致性和真实性,再通过集中式数据融合实现有效信号重构和消噪信号的输出。
1.2 声阵列时延矢量封闭准则
假设阵列中各传声器分别为i,j,k,l,如图1所示,根据声信号传播的时延估计特性可知,信号到达各传声器的时间存在一定的时延,由于弹载声阵列中各传声器之间距离远小于声源到达阵列的距离,因此,以某一传声器为基准,各传声器时延矢量按逆时针可形成一种矢量封闭的四边形,该四边形就代表了时延矢量封闭准则,即:
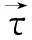
(1)
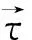
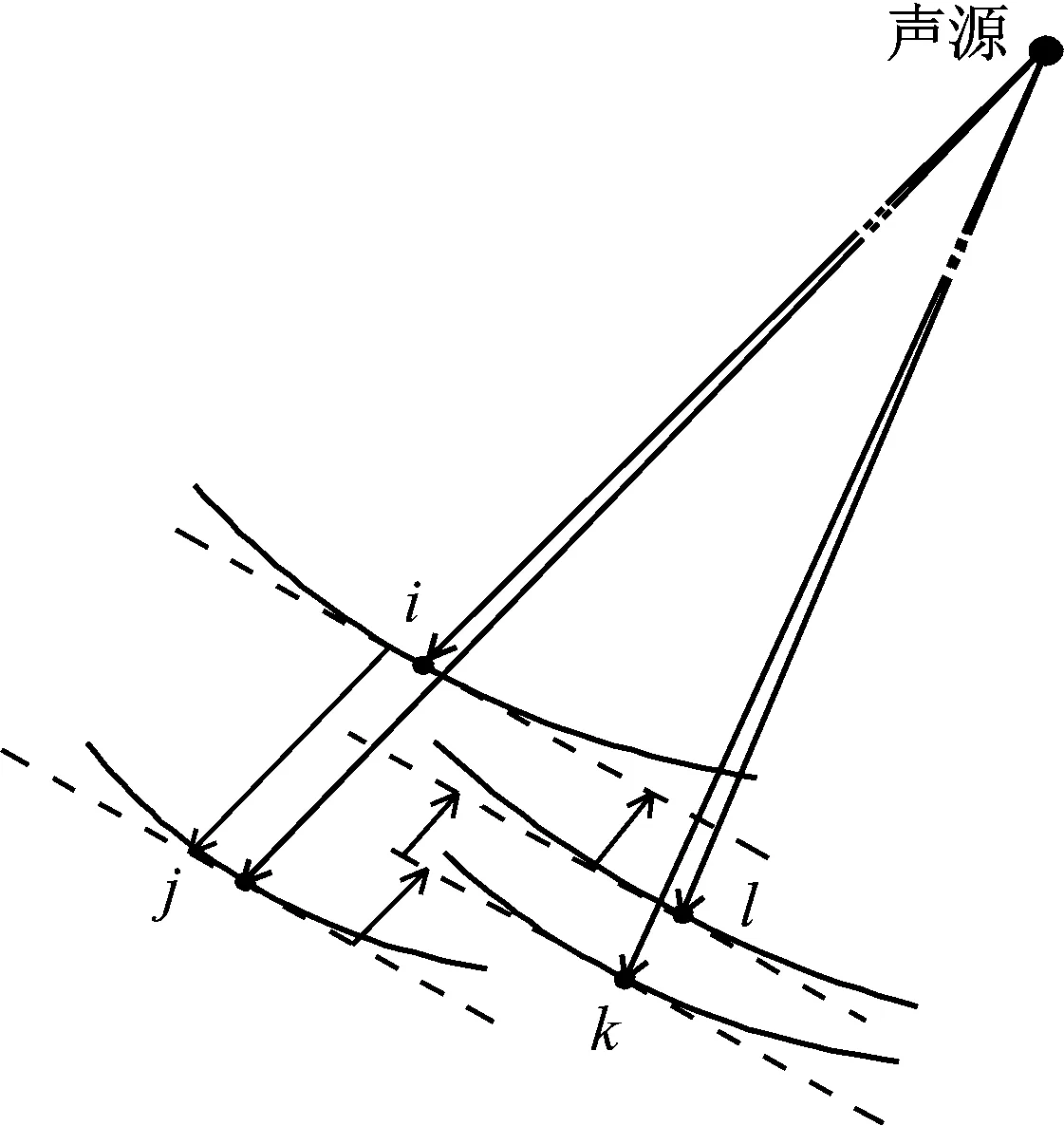
图1 声信号时延矢量封闭示意图
2 EEMD算法及其改进
2.1 EMD及EEMD理论
EMD方法是一种自适应信号处理方法,根据非线性、非平稳信号的自身特征时间尺度,将复杂信号分解为若干有限固有模态函数(Intrinsic Mode Function,IMF)和一个余项之和,各阶IMF相邻零点之间的每一个波动周期中只有一个单纯的波动模式,反映了原始信号中包含的不同频率成分,表征信号所包含的真实物理意义,而余项表示信号的趋势。设声信号为x(t),则EMD分解成n阶IMF分量后可表示为:
(2)
式中:ci(t)表示第i个IMF分量;rn(t)为余项;各IMF分量按频率从高到低顺序排列。
然而,在被动声信号检测过程中,由于信号频率分布的间歇性或非平稳信号与噪声之间的耦合作用,EMD在实测信号分解时常伴有模态混叠现象,即单个或多个IMF分量中会包含差异极大的特征时间尺度,或相近的特征时间尺度被划分到不同IMF中。以文献[18]的坦克声信号为例,采用传统EMD方法进行分解的结果如图2(a)和(b),原始信号经EMD分解为11个IMF分量,图3(a)和(b)给出各分量归一化功率谱,信号主要频率成分已被全部分解出来,但分量IMF2、IMF3以及IMF4均包含了多种频率成分,此外,185.5 Hz、29.3 Hz和9.77 Hz低频成分有同时出现在多个IMF分量中,可以判定该信号EMD分解过程中出现了较为严重的模态混叠效应,会增加实测信号分析的错误发生率,应当尽量避免。
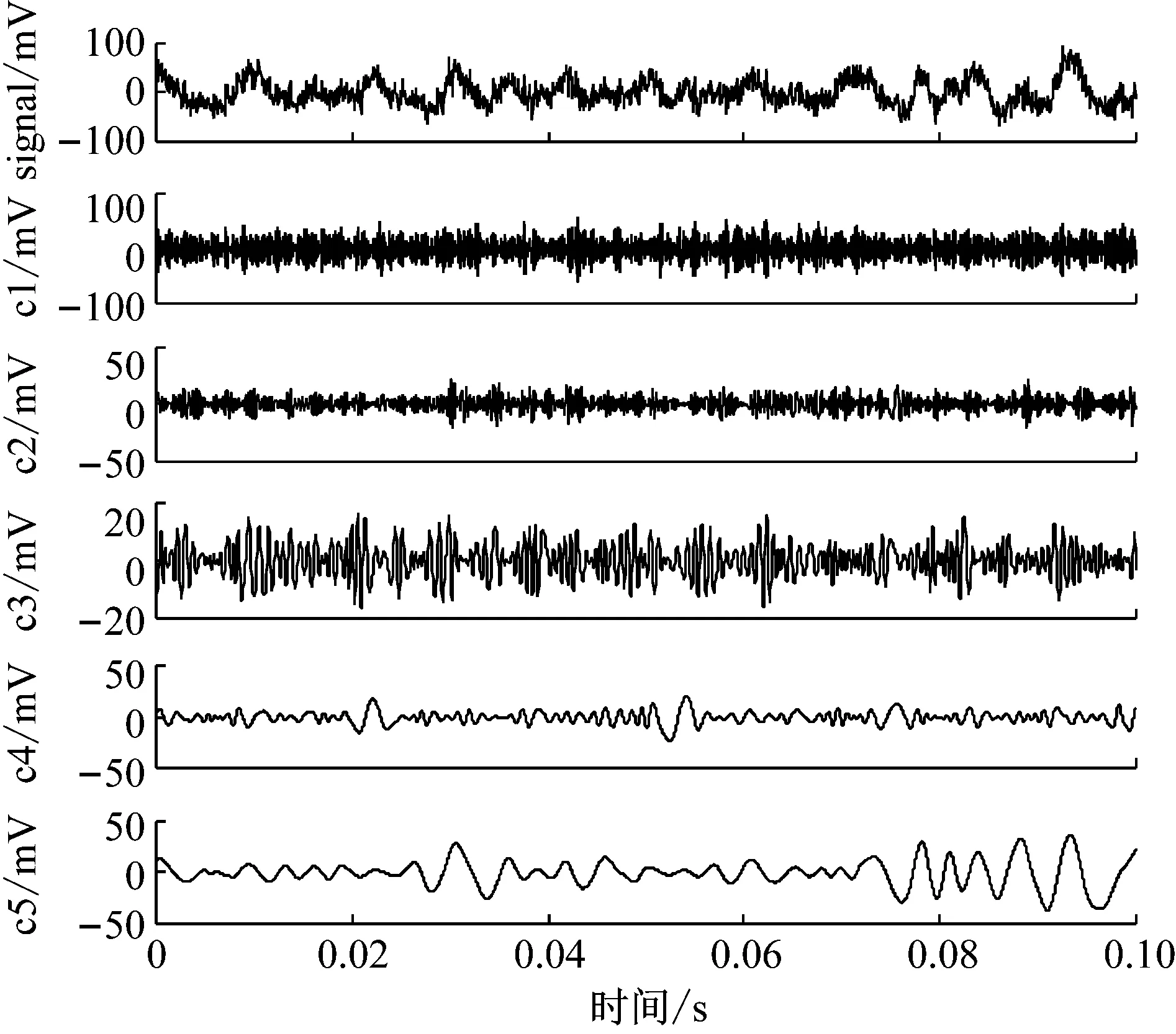
(a) 某坦克声信号及其EMD分量IMF1-IMF5
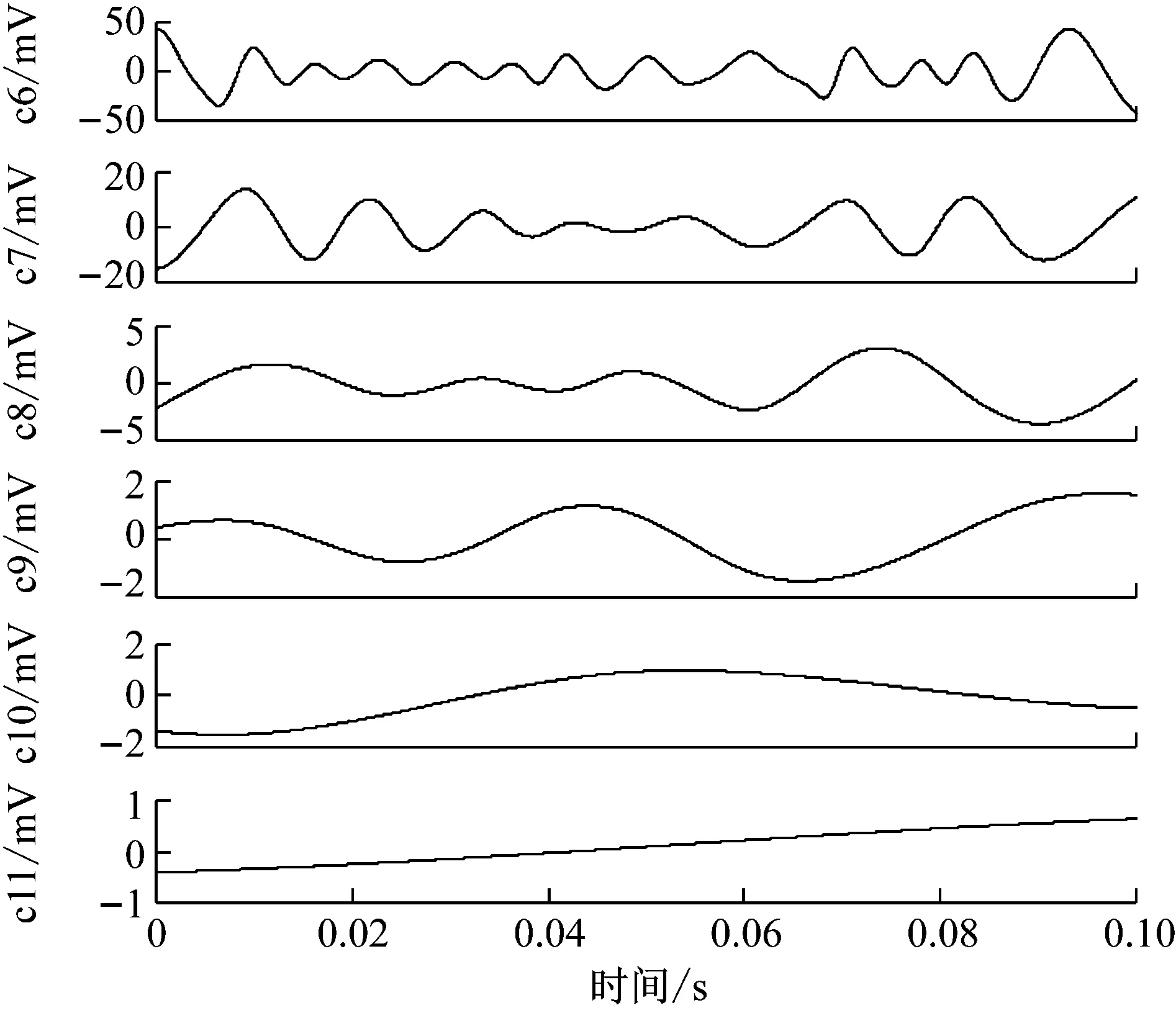
(b) EMD分量IMF6-IMF11
Wu在2009年提出了集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD),利用高斯白噪声具有频率均匀分布的特性,使得含噪信号在不同频率尺度上具有连续的特性,有效抑制EMD分解造成的模态混叠现象。声信号EEMD分解具体步骤为:
(1) 在原始信号x(t)中加入均值为0,标准差为常数的高斯白噪声后得到总体信号X(t),对X(t)进行EMD分解,得到n′阶IMF分量:
(3)

(a) 分量IMF1-IMF6对应归一化频谱
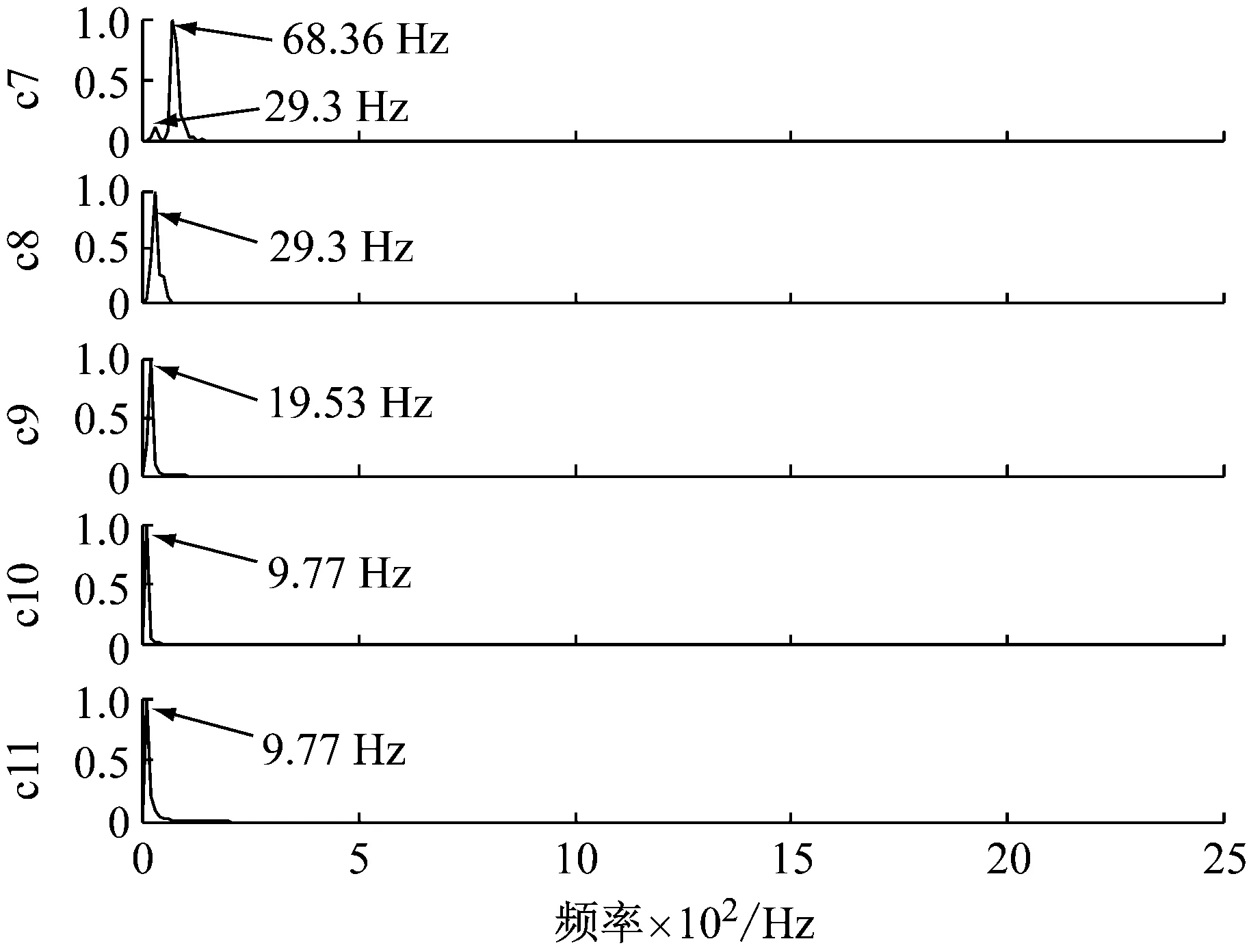
(b)分量IMF7-IMF11对应归一化频谱
(2) 给原始信号x(t)加入不同高斯白噪声hj(t),重复步骤(1)M次,得到第j次分解结果:

(4)
(3) 根据高斯白噪声频谱具有的零均值原理,减弱白噪声作为时域分布参考结构所产生的影响,原始声信号的各阶IMF分量可表示为:
(5)
根据张雪英等的研究,EEMD中加入高斯白噪声的次数服从式(6)的统计规律

(6)
式中:M为加入高斯白噪声的测试;ε为噪声幅值系数;εn′为原始声信号与各IMF分量之间的误差。
(4) 原始声信号x(t)分解为:
(7)
EEMD方法主要利用高斯白噪声具有频率均匀分布的统计特性来解决模态混叠问题。由于白噪声具有在各个频段能量一致和均值为零的特性,通过在原始信号中引入白噪声后再进行EMD分解可以保证分解得到每阶IMF分量在时域上的连续性。在原始信号中循环引入足够多组不同的白噪声后,经过EMD分解可以得到多组IMF分量,对各组IMF分量分别求取平均值后作为最终分解结果。
2.2 基于多传声器最小有效频率的EEMD算法
由于EEMD是在EMD基础上进行改进,需要进行循环导入高斯白噪声并反复分解,难免造成信号“过分解”或引入虚假成分,因此,必须考虑EEMD方法的信号分解效率,即:IMF筛分终止条件问题。陈仁祥等在标准EEMD的基础上针对单传感器信号提出了一种考虑频率截止的EEMD方法,以原始信号本身的最小频率作为终止条件,该方法可有效减少IMF分量的过分解,提高EEMD的分解效率,那么本文将引入最小频率截止思想,提出一种针对多传声器阵列信号的多通道最小有效频率的EEMD算法。具体步骤如下:
(1) 假设声阵列包含N个传声器,对多传声器信号xi(t),i=1,2,…,N分别进行功率谱分析,得到各个通道信号频谱中的最小频率,并以其中最小者作为各通道信号分解的截止频率,记为fmin;
(2) 给各信号xi(t)分别加入一定幅值的高斯白噪声υk(t),即
Xi,k(t)=xi(t)+υk(t)
(8)
(3) 对各通道信号Xi,k(t)进行EMD,每分解出一个IMF分量ckji(t),对ckji(t)作频谱分析,并确定其主要频率fkji,比较该分量主要频率和fmin的大小,若fkji小于fmin,停止分解,否则继续。由此得到一次加噪EMD的IMF分量组c11i,c12i,…,c1ji,其中,j表示IMF分量的阶数;
(4) 对各通道信号连续进行K次加噪EMD,得到K组IMF分量,计算K次分解的IMF的总体均值,得到M层IMF分量,即为传声器信号xi(t)经过EEMD分解的最终IMF分量,即:

(9)
需要说明的是,目标信号的最小有效频率选取应适当结合目标振动信号的主要频率成分和信号能量谱的主要分布来确定,防止因噪声干扰造成的虚假频率成分所产生的影响。
3 信息融合辅助改进EEMD的多传声器信号去噪
假设传声器组有N(N≥4)个传声器,首先进行声阵列初始化,根据多传声器信号数据一致性,对所用传声器分别进行性能评估,给出多传声器综合支持度λ=[λ1,λ2,…,λN],进而确定最优传声器组。
令各传声器信号为xi(t),对所有信号进行功率谱分析,得到最小频率fmin作为EEMD的筛分截止频率,对所有传声器信号进行最小频率EEMD分解,所得各通道信号的IMF分量阶数为M=[M1,M2,…,MN],取M=min(M1,M2,…,MN)层IMF分量进行去噪处理。
将相邻传声器的对应层IMF进行互相关时延计算,那么所有传声器信号的第j层IMF分量引起的时延差为:
τj=τ12+τ23+…+τN-1,N+τN,1,j=1,2,…,M
(10)
由式(10)进一步得出传声器组M层IMF分量的时延差向量τ:
τ=[τ1,τ2,…,τM]
(11)
由于环境噪声的普遍存在性,则其一定不满足矢量封闭准则,因此,矩阵可以有效反映出EEMD分解后,多传声器信号在不同尺度上的信号相关程度。结合多传声器综合支持度向量λ,确定各阶IMF的权重阈值θ,
(12)
定义各层IMF权重为:
(13)
得到总体IMF分量对应的权值矩阵为:
R=[r1,r2,…,rM]
(14)
由该矩阵可以发现,目标信号应为满足时延矢量封闭性的信号,而权重趋于零的IMF分量即为噪声。最后,将各阶IMF乘以相应权值,再按式(15)进行信号重构,便能够得出真实信号估计值,即降噪信号。

(15)
4 试验信号分析
为了验证对本文所提算法的可行性和有效性,进行了相应的半实物仿真试验,采用同类同介质传声器,设计平面四元声阵列,图4为声阵列试验设计图。阵列半径为25 cm,四个传声器S1、S2、S3和S4对称分布于圆形平面,对称阵元连线相互垂直。以某坦克目标声信号作为声源样本S,平面四元声阵列水平放置于测试点M,声源距离阵列中心333 cm,方向角为90°,声源及声阵列均保持静止。
声阵列实物结构如图5所示,阵面平台分为均匀的12个区域,相邻区域辐射角度为30°。四个双模预极化自由场传声器(型号:CHZ-213)对称分布于圆形平面,对称阵元连线相互垂直。采用PXI数据采集系统对声信号进行采集,采样频率为62.5 kHz,量程为-4 V~+4 V,声阵列中四个阵元分别对应于PXI测试仪的四个信号采集通道,因此所采集到的声信号为四通道信号。
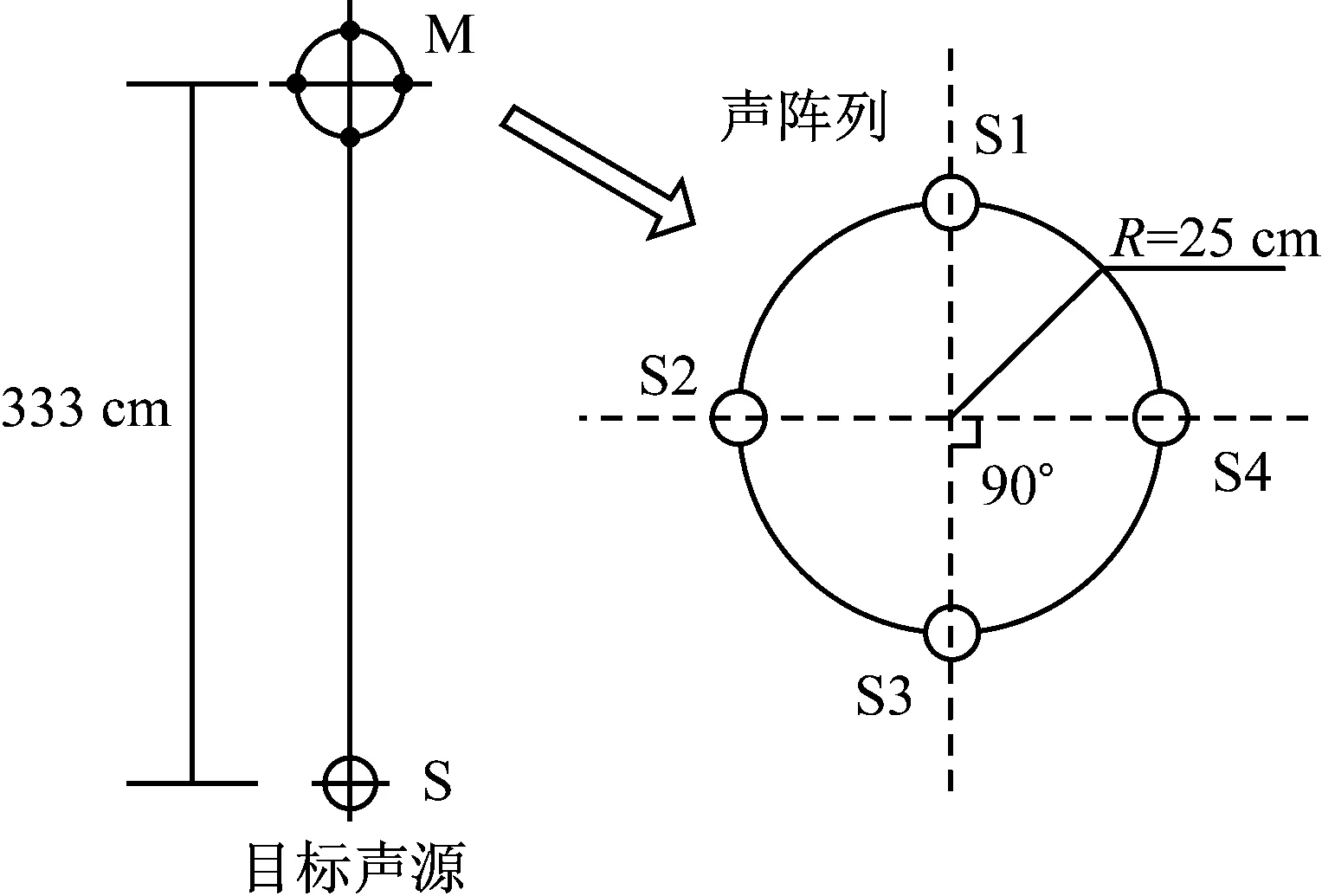
图4 声阵列试验原理图

图5 平面四元声阵列实物图
原始四通道信号及各通道信号对应频谱如图6所示,chn1~chn4分别来自于传声器1~传声器4的测量信号,可以明显发现传声器1的测量信号曲线及其频谱与其他测量信号明显不同,初步估计为传声器1特性不同于其他传声器或传声器1失效,通过传感器数据一致性计算各传声器综合支持度,可以确定最优传声器组为传声器2、3和4,传声器1作为备选。
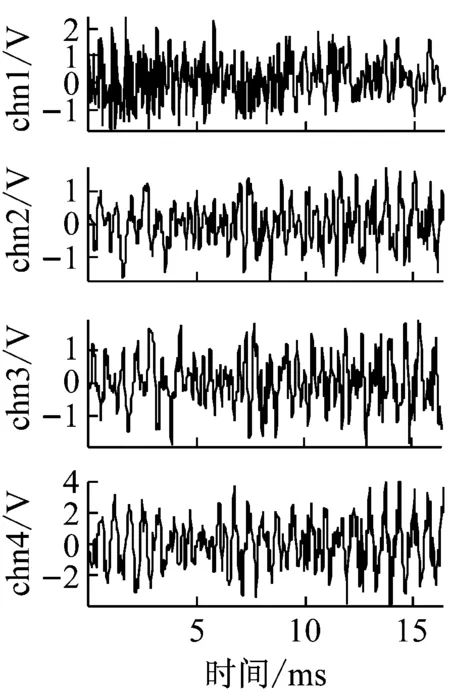
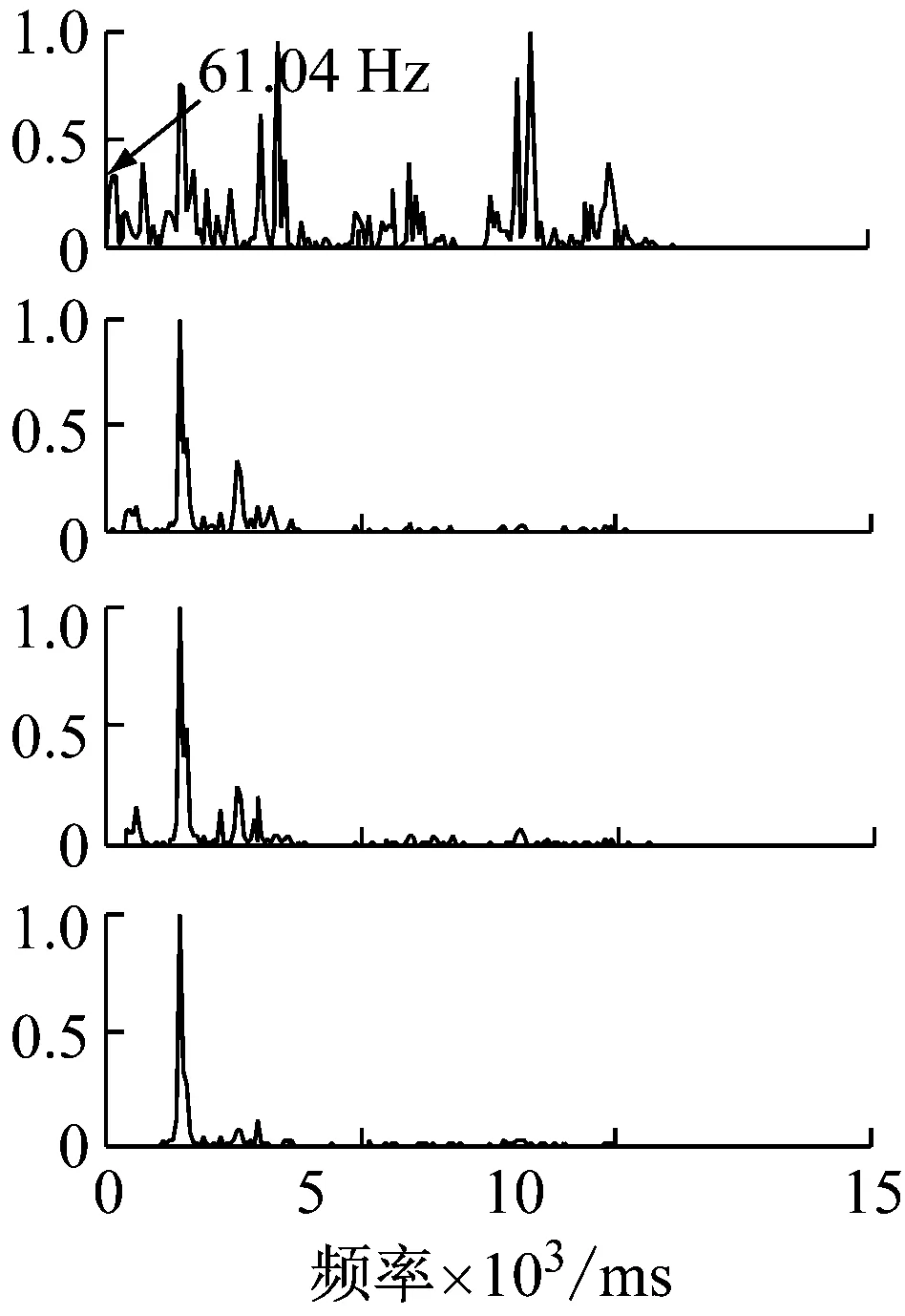
图6 四通道信号及其归一化频谱
由于目标声信号为某坦克辐射声信号,相关研究表明,坦克声信号主要有空气动力噪声和机械振动噪声组成,其中机械振动为主要噪声源。坦克信号一般为宽带信号,其能量谱为中低频连续谱,主要能量集中于1 000 Hz以内,发动机噪声的周期性在频域表现为一组窄带的谐波线。另外根据能量谱中各频率成分的统计发现,振动信号在200 Hz以下的低频段仍有较为明显的特征峰值,中频噪声则由基频的高次谐波延伸所致。
因此,结合坦克目标的振动特征,统计四通道信号的最小有效频率分别为61.04 Hz、122.1 Hz、183.1 Hz和122.1 Hz,则选取通道1的61.04 Hz作为EEMD多通道信号分解的终止频率,对通道1、2、3和4的信号进行分解,图7~图14分别为通道1~通道4信号经过
多传声器最小有效频率截止的EEMD分解结果及各通道分量频谱。由图7~图10可以看出,经过本文改进EEMD算法的分解各通道信号IMF分量数为6~7个,分量个数较EMD分解减少近一半。
再由图11~图14中各分量归一化频谱发现,改进EEMD已将多通道信号的主要频率成分分解出来,由于坦克主要频率成分分布于2 000 Hz以内,则各通道IMF1分量可视为高频噪声,在各阶分量互相关及权重计算时可不作考虑。着重考察最优传声器组2、3和4的信号分解频谱,如图12、图13和图14所示,各通道信号分解余量均为61.04 Hz,而通道2最小频率分量为IMF7=122.6 Hz,通道3为IMF6=183 Hz以及通道4为IMF7=122 Hz,该结果与原始信号谱分析结果相吻合。

图7 通道1信号最小有效频率截止EEMD分解结果
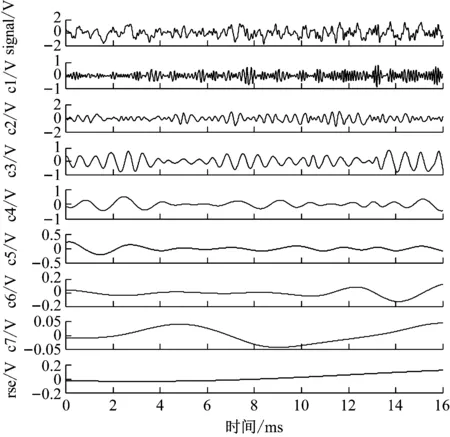
图8 通道2信号最小有效频率截止EEMD分解结果

图9 通道3信号最小有效频率截止EEMD分解结果
经过改进EEMD的信号分解后,计算相邻传声器的对应层IMF互相关时延,结合多传声器综合支持度向量λ=[0.246 0,0.251 9,0.252 0,0.250 1],确定各阶IMF的权重阈值θ=0.25,进而得到总体IMF分量对应的权值矩阵R=[0,0,0,1,1,1,1],最后将各阶IMF乘以相应权值,得到各通道信号的重构信号,如图15所示。
为了方便分析本文算法去噪效果,规定降噪信号与原始信号能量比、算法运行时间及信号分量阶数作为算法降噪效果的衡量参量,其中能量比是降噪信号能量与原信号能量的比值,衡量去噪信号中所包含信息量,直接反映算法去噪水平,若能量比过大,则表明去噪后信号中尚有噪声成分可能未能滤出;若能量比过小,则表明去噪后信号中不仅滤除了噪声成分,也抑制了部分有用信号。运行时间及分量阶数则反映了算法计算速度及效率。

图10 通道4信号最小有效频率截止EEMD分解结果
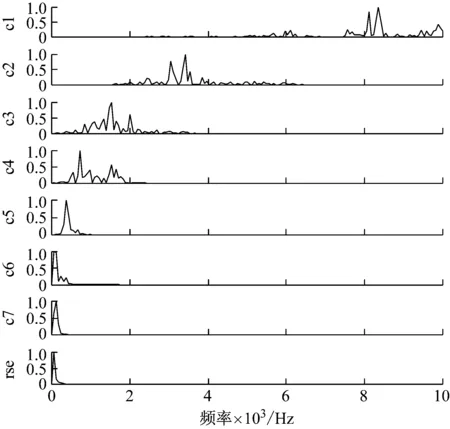
图11 通道1信号最小有效频率截止EEMD分量归一化频谱
Fig.11 Normalization frequency spectrum of channel 1 signal IMFs by minimum frequency cut-off EEMD
图15为坦克四通道信号及其基于信息融合辅助改进EEMD的降噪结果,图16为仅采用传统EMD的降噪结果。表1给出了两种方法在降噪水平及降噪效率方面的量化对比。表2为本文算法对声阵列各传声器信号去噪的基本特征量化统计。
由表1可以看出,传统EMD的信号分解阶数和算法运算时间都明显大于本文所提的信息融合辅助改进EEMD算法;在平均能量比方面,传统EMD降噪能量比大于改进EEMD的降噪能量比,但实际上传统EMD降噪能量比值过大,而本文算法降噪后能量比为合理值。通过图15和图16比较同样能够发现,传统EMD在多传声器实测信号降噪中去噪效果并不明显,说明未能有效滤除噪声,而本文算法实现了对原信号的有效降噪,此外,结合目标振动信号的能量分布状况[1]可知,坦克声信号的能量主要集中于100 Hz~500 Hz的中低频段内,这也同样表明了本文所提算法也最大限度的保留了原始信号中的有用信息。
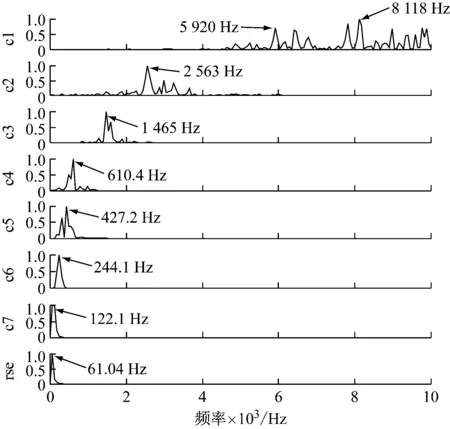
图12 通道2信号最小有效频率截止EEMD分量归一化频谱
Fig.12 Normalization frequency spectrum of channel 2 signal IMFs by minimum frequency cut-off EEMD

图13 通道3信号最小有效频率截止EEMD分量归一化频谱
Fig.13 Normalization frequency spectrum of channel 3 signal IMFs by minimum frequency cut-off EEMD
将本文所提算法的多通道信号去噪结果与原始信号进行对比统计,结果如表2所示,通道Chn2、Chn3以及Chn4原始信号经信息融合辅助的改进EEMD方法去噪后的重构信号分别在均值、最大值及最小值三个因素的相对误差均小于5%,并且这三个通道的重构信号相对剩余能量均保持在90%左右,说明重构信号较好地保留了目标信号的基本特征(均值、最大值、最小值及能量值)。
Fig.14 Normalization frequency spectrum of channel 4 signal IMFs by minimum frequency cut-off EEMD


图15 四传声器原始信号及改进EEMD去噪信号
Fig.15 Original signal and the relevant de-noising results of four sensors by improved EEMD
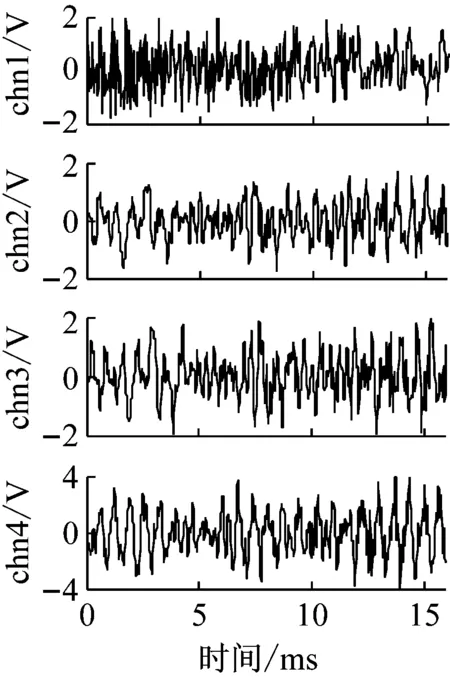
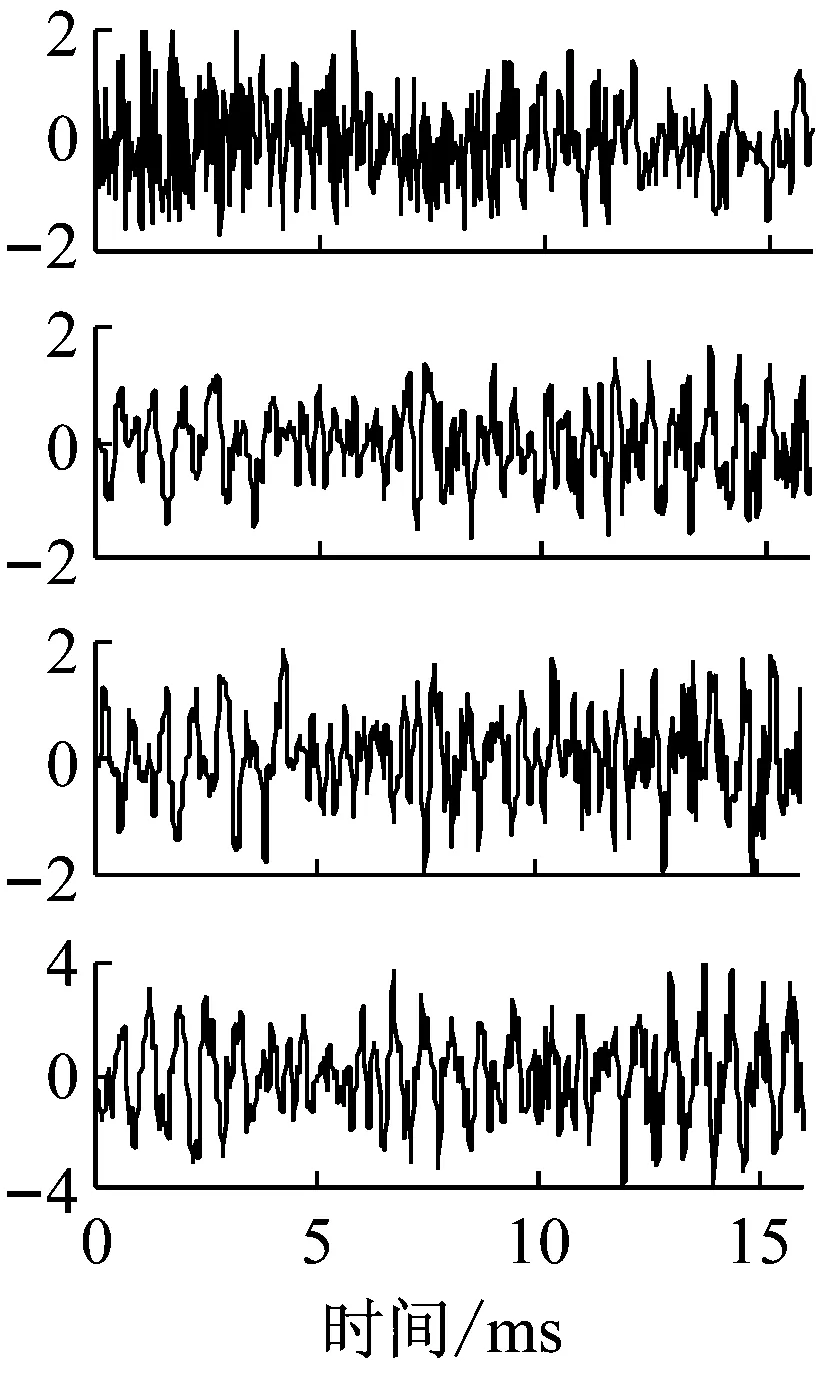
图16 四传声器原始信号及传统EMD去噪信号
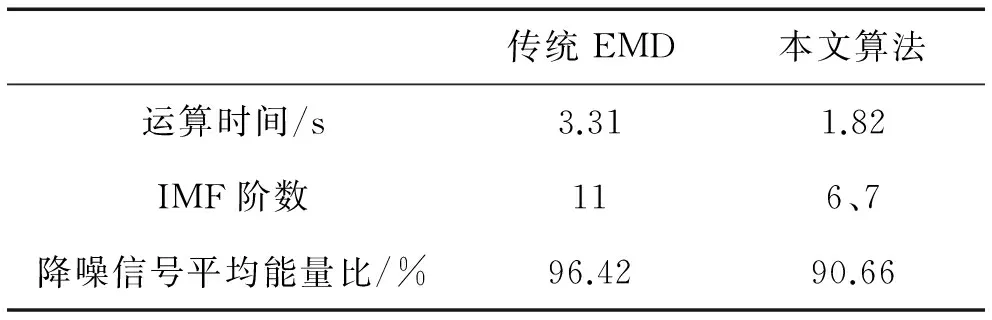
传统EMD本文算法运算时间/s3.311.82IMF阶数116、7降噪信号平均能量比/%96.4290.66
值得注意的是,在表2中,通道1重构信号的基本特征相对误差很大,基本超过了21%,远大于其他通道重构信号的同类特征,说明通道1的原始信号受到了较多的噪声干扰而造成了信号失真,进一步反映了该声阵列中传声器1处于支持度较低(故障或失效)的状态,这正是多传声器数据一致性融合的综合支持度计算结果的另一个角度的体现。
因此,基于信息融合辅助最小有效频率EEMD的多传声器阵列信号去噪方法能够有效的抑制阵列信号中的噪声干扰,提高了信号分解及降噪效率,较好地保留原始信号中的有用信息,而且在一定程度上优化了声阵列中的传声器资源配置,综合支持度高的传声器信号得到增强,而综合支持度低的传声器信号受到了抑制。

表2 信息融合辅助改进EEMD对各通道信号去噪效果统计
5 结 论
本文针对多传声器阵列信号降噪问题提出一种基于多传声器信息融合辅助改进EEMD的被动声信号去噪方法。
(1) 提出了一种新的多传声器EEMD信号分解方法,该方法采用多通道信号总体最小有效频率作为IMF分量的筛选终止条件,在实测信号分解时,大幅减少IMF分量阶数,同时较好地克服了传统EMD信号分解产生的模态混叠效应,有效抑制标准EEMD分解时引入的冗余虚假分量,从而提高信号去噪效率。
(2) 根据多传声器时延估计特性,引入声信号时延封闭准则,结合数据一致性融合理论及阵列信号相关系,对多传声器各层IMF分量赋予合理化权重,对各分量重构后实现多通道信号去噪。
(3) 通过静态四元平面声阵列试验表明,本文所提的多传声器信息融合辅助改进EEMD信号去噪方法具有良好的去噪效果,同时优化了多传声器资源配置,为下一步声阵列目标探测的工程实现提供一种可靠的理论方法。
[1] 吕艳新. 被动声目标识别理论研究[D]. 南京:南京理工大学,2011.
[2] 申永军,杨绍普,张光明. 基于分数Fourier变换的自适应信号降噪方法[J]. 振动工程学报,2009,22(3): 292-297.
SHEN Yongjun, YANG Shaopu, ZHANG Guangming. Adaptive noise reduction method on frational Fourier transform[J]. Journal of Vibration Engineering, 2009, 22(3): 292-297.
[3] ALVANITOPOULOS P F, PAPAVASILEIOU M, ANDREADIS I, et al. Seismic intensity feature construction based on the Hilbert-Huang transform[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(2):326-337.
[4] 章浙涛,朱建军,匡翠林. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报,2014,43(1):13-20.
ZHANG Zhetao, ZHU Jianjun, KUANG Cuilin. Multi-threshold wavelet packet de-noising method and its application in deformation analysis[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 13-20.
[5] 阳子婧,蔡力钢,高立新. 自适应冗余提升小波降噪分析及其在轴承故障识别中的应用[J]. 振动与冲击,2013,32(7):54-57.
YANG Zijing, CAI Ligang, GAO Lixin. Adaptive redundant lifting wavelet de-noising analysis and its application in bearing fault identification[J]. Journal of Vibration and Shock, 2013, 32(7):54-57.
[6] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, 1998, 5454: 903-995.
[7] LÜ Y X, GU X H. An adaptive noise cancelling method based on EMD for acoustic in battlefield[C]. The 8th International Congress on Image and Signal Processing, 2009: 4053-4056.
[8] 贾瑞生,赵同彬,孙红梅,等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报,2015,58(3): 1013-1023.
JIA Ruisheng, ZHAO Tongbin, SUN Hongmei. Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis[J]. Chinese Journal of Geophysics, 2015,58(3): 1013-1023.
[9] ALVANITPOOULOS P F, PAPAVASILEIOU M, ANDREADIS I, et al. Seismic intensity feature construction based on the Hilbert-Huang transform[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(2): 326-337.
[10] 苏文胜,王奉涛,张志新,等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击,2010,29(3): 18-21.
SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3): 18-21.
[11] 汤宝平,董绍江,马婧华. 基于独立分量分析的EMD模态混叠消除方法研究[J]. 仪器仪表学报,2012,33(7): 1477-1482.
TANG Baoping, DONG Shaojiang, MA Jinghua. Study on the method for eliminating mode mixing of empirical mode decomposition based on independent component analysis[J]. Chinese Journal of Scientific Instrument, 2012, 33(7): 1477-1482.
[12] 赵志宏,杨绍普,申永军. 一种改进的EMD降噪方法[J].振动与冲击,2009,28(12): 35-37.
ZHAO Zhihong, YANG Shaopu, SHEN Yongjun. Imporved EMD based de-noising method[J]. Journal of Vibration and Shock, 2009, 28(12): 35-37.
[13] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[14] 陈仁祥,汤宝平,马婧华. 基于EEMD的振动信号自适应降噪方法[J]. 振动与冲击,2012,31(15): 83-86.
CHEN Renxiang, TANG Baoping, MA Jinghua. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal[J]. Journal of Vibration and Shock, 2012, 31(15): 83-86.
[15] 黄杰,张梅军,柴凯,等. 基于频率截止的EEMD方法研究[J]. 振动与冲击,2015,34(8): 101-105.
HUANG Jie, ZHANG Meijun, CHAI Kai, et al. An improved EEMD method based on cut-off frequency[J]. Journal of Vibration and Shock, 2015, 34(8): 101-105.
[16] ZHENG J D, CHENG J S, YANG Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing[J]. Signal Processing, 2014, 96: 362-374.
[17] 张雪英,谢飞,乔铁柱,等. 基于EEMD与改进小波阈值的磁记忆信号降噪研究[J]. 太原理工大学学报,2015,46(5): 592-597.
ZHANG Xueying, XIE Fei, QIAO Tiezhu, et al. Denoising algorithm for metal magnetic memory signals based on EEMD and improved semi-soft wavelet threshold[J]. Journal of Taiyuan University of Technology, 2015, 46(5): 592-597.
[18] 吕艳新,顾晓辉. 多传声器小波多尺度信息融合滤波算法[J]. 仪器仪表学报,2012,33(4): 788-794.
LÜ Yanxin, GU Xiaohui. Filtering algothm for multi-microphones based on wavelet multi-scale information fusion[J]. Chinese Journal of Scientific Instrument, 2012,33(4): 788-794.
[19] DI Y,GU X H. A data consistency method for multiple acoustic sensors based on frequency spectrum similarity algorithm[C]//IEEE Advanced Information Technology, Electronic and Automation Control Conference, 2015: 1161-1166.
A signal de-noising method for multi-microphone array based on information fusion and improved EEMD
DI Yi1, GU Xiaohui1, LONG Fei2
(1.School of Mechanical Engineering, Nanjing University of Sci. & Tech. Nanjing 210094, China;2. Institute of Intelligent Information Processing, Guizhou University, Guiyang 550025, China)
Aiming at multi-microphone signal de-noising problem in acoustic array, a signal de-noising method based on information fusion and improved ensemble empirical mode decomposition (EEMD) was proposed here. Firstly, an improved EEMD algorithm taking the ensemble minimum effective frequency of multi-channel signals as the cut-off frequency of EEMD was introduced. Original signals were decomposed rapidly into complete IMF components with the improved EEMD algorithm to suppress effectively mode mixing phenomena and false IMF components. Secondly, through introducing the time delay vector close rule(TDVCR) and the data consistency fusion theory, the weight matrix of IMFs was computed according to the correlation of corresponding IMFs, and then the de-noising signals were reconstructed with the weighted IMF components. Finally, through the semi-physical simulation tests of acoustic array and comparing with the traditional EMD signal de-noising, the effectiveness and applicability of the proposed method were verified.
acoustic array; signal de-noising; ensemble empirical mode decomposition (EEMD); data consistency fusion; time delay vector close rule (TDVCR)
国家自然科学基金(61263005)
2016-04-08 修改稿收到日期:2016-06-11
邸忆 男,博士生,1987年10月生
顾晓辉 男,博士,教授,1964年2月生 E-mail:gxiaohui@njust.edu.cn
文献标志码: A DOI:10.13465/j.cnki.jvs.2017.15.020
