基于修正BW模型的战斗部爆炸破片形成机理研究

李 营， 吴卫国， 杜志鹏， 张 玮， 张春辉， 张 磊

(1.武汉理工大学 交通学院，武汉 430063；2.海军装备研究院，北京 100161)

基于修正BW模型的战斗部爆炸破片形成机理研究

李 营1,2， 吴卫国1， 杜志鹏2， 张 玮2， 张春辉2， 张 磊1

(1.武汉理工大学 交通学院，武汉 430063；2.海军装备研究院，北京 100161)

膨胀环是研究战斗部爆炸破片形成机理的重要手段。通过引入修正的B-W内聚力断裂模型ABAQUS子程序，开展了膨胀环碎裂过程的数值仿真计算，并将整个膨胀碎裂过程划分为四个阶段，并讨论了膨胀速度对破片质量分布和破片数量的影响，进一步研究了厚度对碎裂模式的影响。得到以下结论：①膨胀碎裂过程可以分为整体塑性、稳定颈缩、局部颈缩发展和最终碎裂形成四个阶段；②破片数量随着初始膨胀速度增加而增大，且质量分布服从Rayleigh分布；③径厚比的变化改变了变形后期的应力状态，薄壳结构的应力以受拉为主，而厚壳结构后期出现剪切应力状态从而使得断裂模式由拉伸径缩失效逐渐过渡到剪切失效。

反舰导弹；膨胀环；爆炸破片；Rayleigh分布；应力三轴度

反舰导弹成为现代军舰的重要威胁。其爆炸产生的高速破片和冲击波是两个主要的载荷，能有效毁伤舱室结构，并对舰用设备和舰员构成重要威胁。研究反舰导弹战斗部爆炸破片形成机理对于准确掌握破片特性，提高舰船防护水平具有重要意义。膨胀环是研究材料碎裂特性和战斗部爆炸破片形成机理的有效手段[1]。采用数值方法辅助开展膨胀环碎裂行为的研究是目前常用的技术手段。数值仿真水平的提高主要通过2个途径实现，分别为建立合理的本构关系更为准确地表征材料的力学行为，另外一种为提高数值计算方法的速度和精度。有关研究表明[2-3]，本构关系表征不准带来的误差远远大于计算方法带来的误差。

断裂准则研究是材料断裂行为研究的基础，已经经历了若干代发展。早期一直采用等效塑性应变方法。Gurson等[4]通过微观空穴形成和扩展的机理分析提出断裂应变与应力三轴度相关。Johnon等[5]提出目前广泛应用的Johnson-cook断裂准则，综合考虑了应力三轴度效应、应变率效应和温度效应，得到学术界的广泛关注，并集成到了DYNA、ABAQUS等商业软件中。Bao等[6]对低应力三轴度区间进行了重大改进，提出了B-W准则，能较为明确地区分延性损伤、剪切失效模式，受到国外学者的广泛重视[7-8]。

目前，已经有一些学者采用数值仿真方法开展膨胀环碎裂特性的研究，但由于断裂准则的选取相对简单，再现复杂碎裂机理和碎裂模式方面仍有待改进。Rusinek等[9]利用ABAQUS对膨胀环碎裂过程进行了仿真，但假设应力应变曲线一旦出现平台就发生断裂，与实际情况不符。Zhang等[10]认为等效塑性应变为1时材料破坏，并采用单元删除方法表征材料失效，此种方法未能反应材料破坏能的破坏机理。陈磊等[12-13]考虑了材料断裂能，并基于Johnson-cook断裂准则利用ABAQUS对韧性膨胀环的膨胀碎裂进行了，得到了破片的平均尺寸，对Grady-Kipp准则进行了验证，但未考虑低应力三轴度区间材料破坏机理的变化对碎裂特性的影响，使得破坏模式的预测不够准确。尚未见到使用B-W准则研究膨胀环碎裂特性的研究，该准则对膨胀碎裂模式影响的研究有待开展。

本文将修正的B-W内聚力断裂模型通过材料子程序方法集成进ABAQUS， 并以此为基础开展了膨胀碎裂的数值仿真研究，讨论了膨胀速度对颈缩演化、破片分布的影响，研究了膨胀环径厚对碎裂模式的影响。

1 爆炸破片形成基本理论

Mott早在1947年就给出了膨胀环破片的基本理论，示意图见图1。圆环在冲击瞬间膨胀半径为r、速度为V0，则此时的应变率为

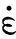
(1)

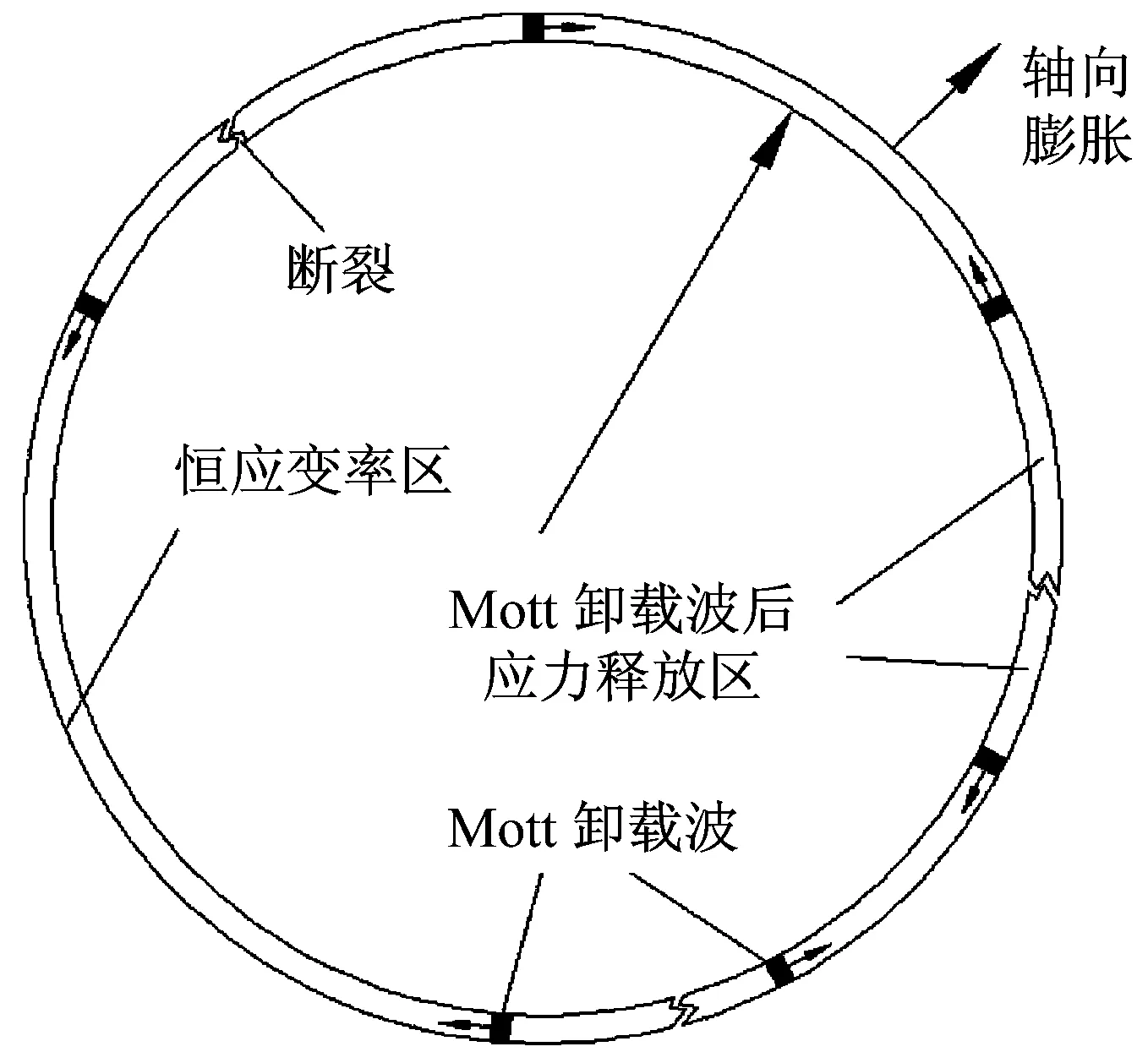
图1 战斗部碎裂示意图

假设有一初始断口，则该处形成自由界面，并形成卸载波。卸载波向两侧传播，并形成一段无应力区。该卸载波的波速为

(2)

Mott给出平均破片长度的预测公式，如下

x0=(2PF/ργ)1/2r/V0

(3)

式中：PF为相应应变率下的流动断裂应力；ρ为材料密度；r为膨胀环半径；v为膨胀速度。

2 低碳钢碎裂破坏的力学特性

2.1 塑性流动准则

Johnson-cook强度模型[14]是一种黏热塑性本构关系，这种模型能较好地描述金属材料的加工硬化效应、应变率效应和温度软化效应。Johnson-cook强度模型的形式为

(4)

塑性温度升高为

(5)

式中：ρ，c分别为材料的密度和比热；β为Taylor-quinney常数，取为0.9。

2.2 内聚力损伤准则

BW模型在JC模型的基础上对应力三轴度区间进行了修正，将应力三轴度对断裂应变的影响进行分段处理。具体公式如下：

(6)

式中：D01、D02、D03为材料参数，通过不同材料试样获得。

作者前期工作中，开展了不同温度、不同应变率、多种应力状态下的材料断裂试验，对应力率效应和温度效应进行修正，得到了采用修正的B-W内聚力失稳断裂准则，具体参数参见文献[15]。用等效塑性应变作为损伤因子D的开动准则。损伤开动的临界应变εd是一个与应力三轴度、应变率及温度相关的量，可以用下式表示

(7)

式中，D01、D02、D03与式(6)相同，D1、D2、D3、D4、D5也为材料的断裂参数，通过一系列材料试验获得。

一旦损伤开动，假定损伤发展随单元内部塑性变形的发展而线性增加，即

(8)

式中：σ0为损伤开动时刻的单元应力，Gc是损伤开动到材料完全失效(D=1)时所需要的断裂能量；up为损伤开动后单元的塑性位移，由下式给出

up=Lmesh(Δεp)

(9)

由此可见，若发生相同的等效塑性应变，大单元尺寸的损伤将超过小尺寸的损伤。事实上，当材料发生一裂纹演化为主的破坏时，局部塑性应变往往集中在小单元内，公式描述的损伤发展模型将材料的抗损伤发展通过材料的断裂能表征，既可以描述材料的分离过程，又可以减少数值计算对网格尺寸的依赖。

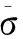
(10)

一旦损伤达到1，材料失去承载力，利用单元消除技术将失效单元消除。

2.3 材料模型验证

采用ABAQUS进行数值仿真计算，通过实验和数值仿真的比对可以看出：改进的BW模型较好再现了Taylor杆高速撞击后较为复杂的花瓣状破坏模式[16]。说明改进的BW模型能较好预测低碳钢在高应变率、复杂应力状态下的损伤失效行为，为进一步开展膨胀环碎裂计算奠定了基础。

定义应力张量的6个分量，更新各时间步中的应力应变参量，通过FORTRAN编译器编写VUMAT材料程序代码，定义应力三轴度、应变率和温度对材料动态损伤特性的影响。在ABAQUS开展计算时，调用子程序开展动态过程计算，并最终得到材料动态碎裂过程及终点效应。

A/MPaB/MPanCmGc/kND01249.28890.7460.0580.9425-6.743D02D03D1D2D3D4D50.0451.3250.2961.184-1.4650.0058.07

3 数值计算

3.1 数值模型

利用ABAQUS建立了膨胀环的三维仿真模型，圆环内径r=20 mm、外径R=21 mm，高度h=1 mm，如图3所示。共划分了10 000个C3D8R单元，其中膨胀环厚度方向上划分5个单元。ABAQUS中总体坐标系为笛卡尔坐标，无法直接加载径向速度，通过Matlab编程实现初始膨胀速度V0。材料参数设置见表1。

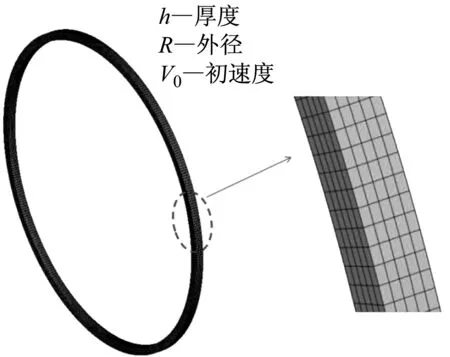
图3 计算模型示意图

3.2 膨胀基本过程

以初速度100 m/s的膨胀环的膨胀过程为例，整个膨胀过程分为四个典型阶段，如图3所示。(Ⅰ)整体塑性阶段(0～18.03 μs)：随着膨胀环膨胀，整体均匀变形，并发生产生较大塑性，塑性温升可达到204 K。(Ⅱ)稳定颈缩阶段(18.03～25.2 μs)：局部区域塑性变形急剧增加，并形成一系列颈缩；非颈缩区域的塑性变形停止，温度不再升高(图5中B点)。(Ⅲ)局部颈缩发展阶段(25.2～29.4 μs)：随着时间的推移，部分颈缩区域快速发展，温度升高进一步加快(如图5中C点)；一部分颈缩则由于相邻快速发展颈缩区形成的卸载波，使得塑性变形受到抑制(Arrested necking)，并最终成为破片中的残余颈缩(图5中A点)；(Ⅳ)最终碎裂阶段(29.4 μs以后)，局部断口形成，碎裂形成阶段。

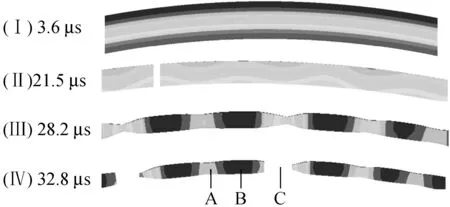
图4 破片形成的四个阶段

图5为不同速度下颈缩发展变化的示意图。当膨胀速度为400 m/s时，单位无量纲周长(该点沿周长方向的距离/膨胀环半径) 上的颈缩为7个，其中有2个颈缩位置后期持续发展，并最终形成断口。当局部颈缩发展越快，对周围颈缩区域的抑制作用越强。

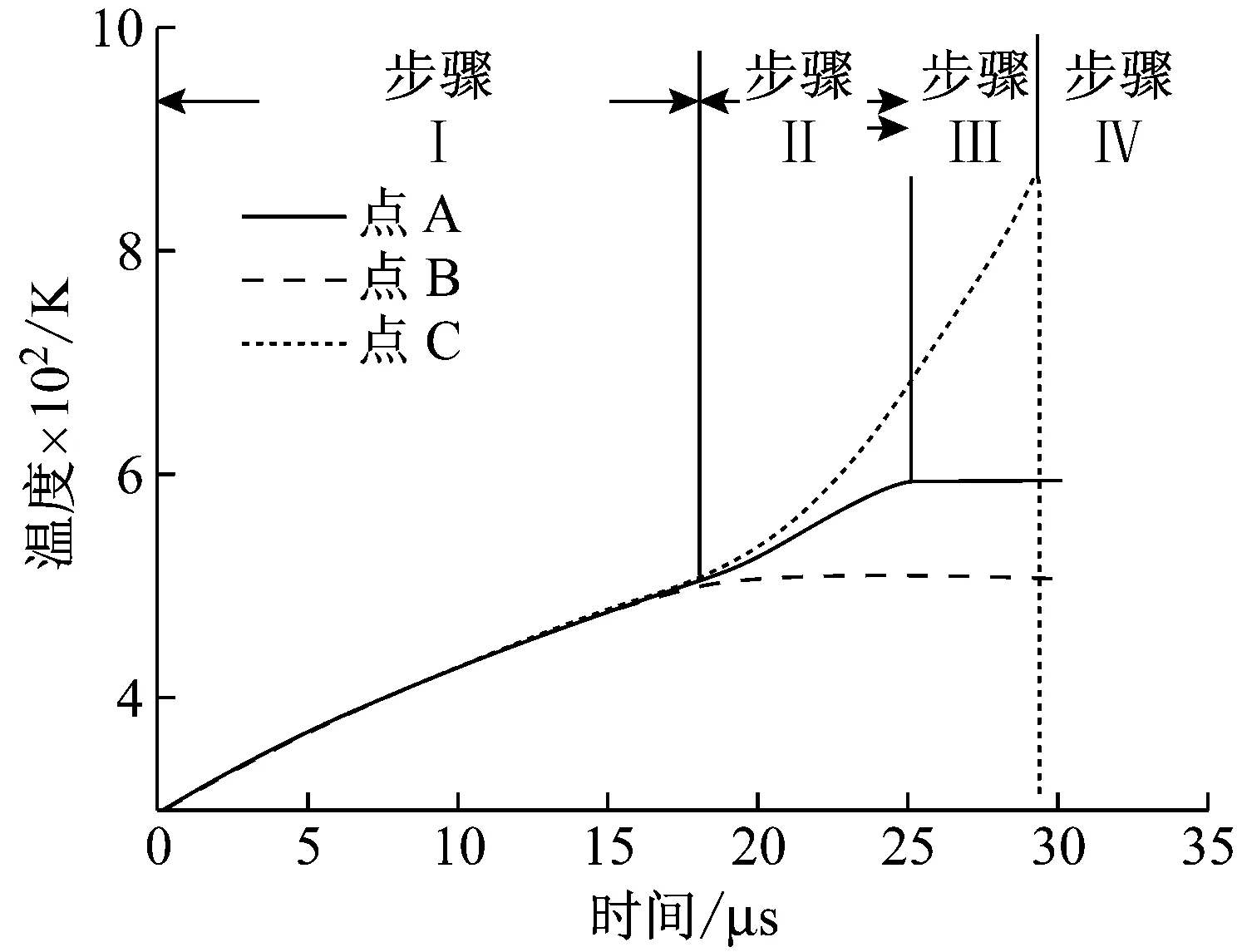
图5 局部区域的塑性温升

当膨胀速度达到100 m/s时，单位无量纲周长上的颈缩为13个，其中5个在后期形成断口，断口形成的自由界面产生mott卸载波，其余颈缩受其作用，应力卸载，塑性变形不再增加。

(a) V0=400 m/s

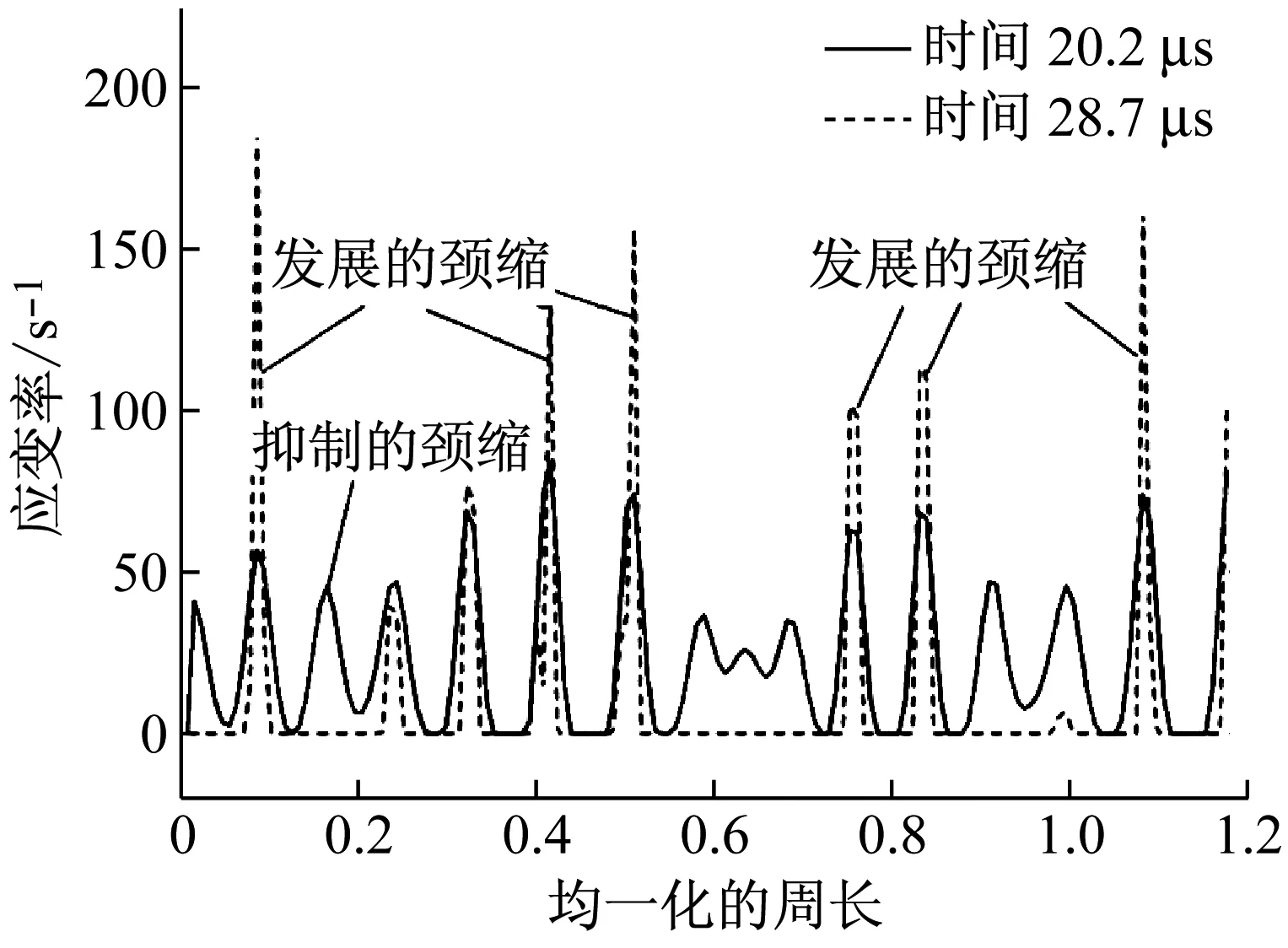
(b) V0=1 000 m/s

3.3 初始膨胀速度对碎裂特性的影响

随着初始膨胀速度的增加，根据公式(1)膨胀环的应变率呈线性增加，材料临界断裂应变发生增大(公式(6))。同时，从公式(2)可以看出，Mott卸载波的传播速度降低，均可对最终碎裂形态有影响。

图7为初始膨胀速度为400 m/s、600 m/s、800 m/s和1 000 m/s的膨胀环碎裂最终形态。可以看出随着初始膨胀速度的增大，破片数量逐渐增多，碎片体积逐渐减小。表2可以看出，相同膨胀速度的膨胀环，最终破片数量接近但不完全相同，每个速度计算5组，统计得到该速度下的破片总数，分别为26、106、147和180个。拟合一次函数直线如图8所示。

图7 不同速度的破片形态

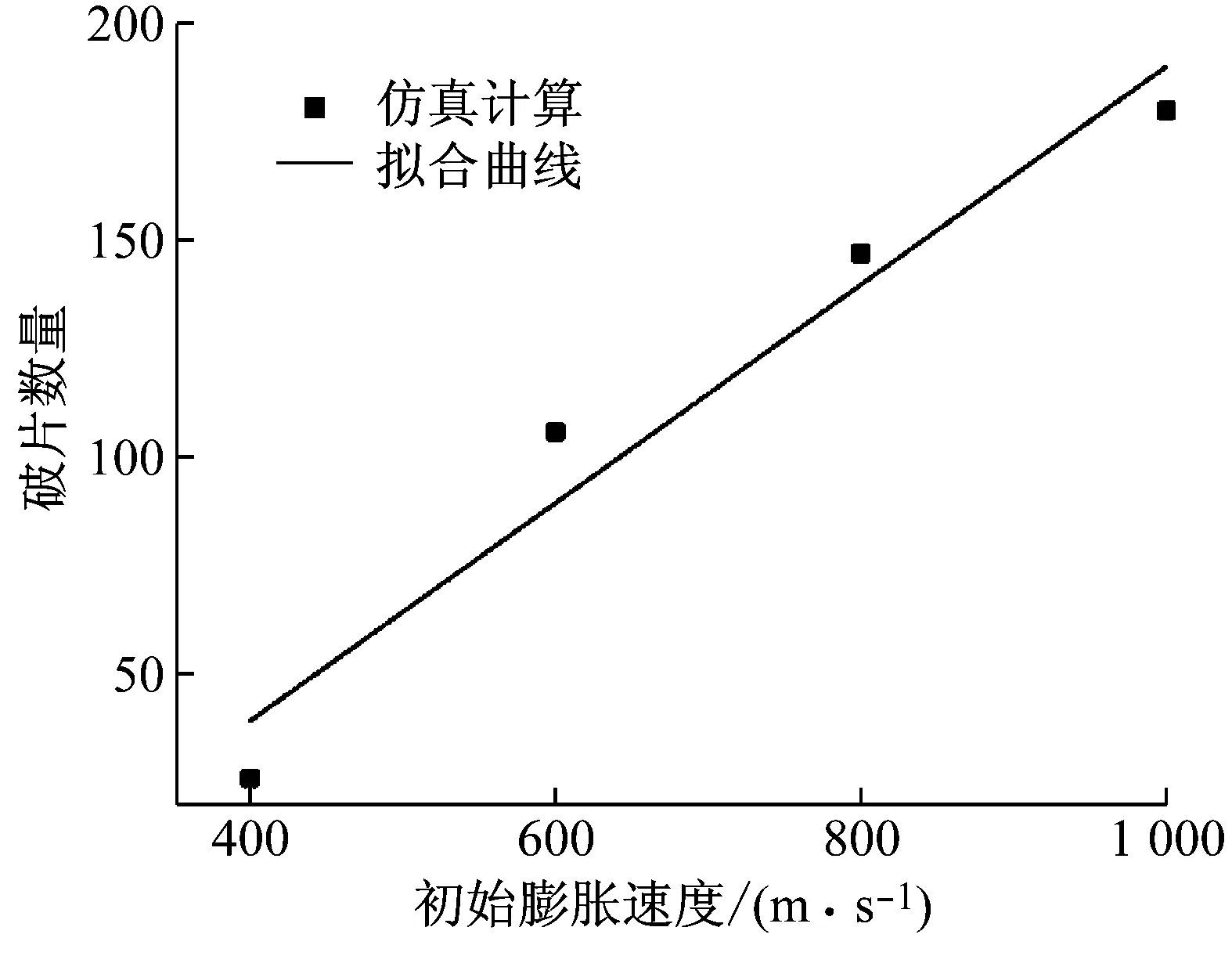
图8 破片数量与初速度的关系

初速度环1破片数环2破片数环3破片数环4破片数环5破片数破片样本数40064565266002221212022106800263129293214710003535333839180

图9为统计不同初速度膨胀环最终破片的质量分布特性。采用n=2的Weibull分布，即Rayleigh分布可以可以较好地表示其破片分布特性[12]，即

相应地，Rayleigh概率密度函数为

(a) 破片质量/g

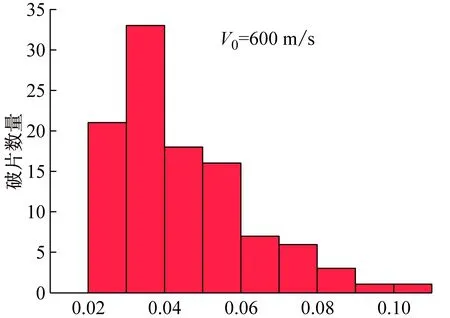
(b) 破片质量/g

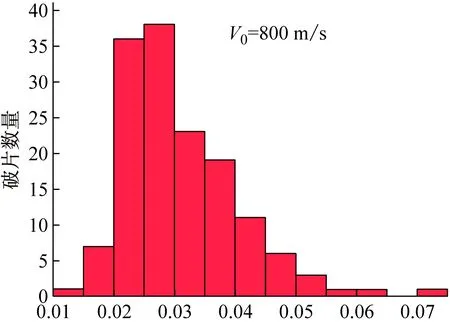
(c) 破片质量/g

(d) 破片质量/g

3.4 厚度对碎裂机理的影响

有关研究表明，薄壳战斗部的破坏模式主要以拉伸失效为主，但也有研究实验中出现剪切为主的失效模式。

开展了径厚比α=R/(R-r)分别为0.05、0.33和0.4，初始膨胀速度均为500 m/s的膨胀碎裂过程模拟。如图10，三种工况分别代表三种典型破坏模式：① 延性颈缩破坏，该破坏模式下，断口颈缩，主要发生延性破坏；② 复合损伤，材料发生延性扩孔破坏和剪切损伤破均存在的复合损伤；③ 剪切损伤，主要机理为形成局部剪切带或绝热剪切带，剪切带与径向方向呈一定角度。

如图11所示，随着α的不同，膨胀环在变形过程中应力状态发生较大改变。在变形初期，膨胀环与单轴拉伸应力状态类似，应力三轴度一直维持在1/3。变形后期，径厚比较小(α=0.05)的环应力三轴度逐渐超过1/3，呈现多轴拉伸趋势；径厚比较大的环应力三轴度逐渐开始下降，并低于0。

应力三轴度与破坏模式的关系如图12所示。已有研究表[1]，σ*<-1/3时，材料受纯压作用，材料不发生损伤；-1/3<σ*<0时，材料受力从纯压向纯剪过度，为压剪联合作用阶段，主要破坏机理为剪切破坏；0<σ*<1/3时，材料受力从纯剪切向拉伸过度，为拉剪联合作用阶段，破坏模式为延性扩孔与剪切混合模式；σ*>1/3时，损伤机理为延性损伤。在区间(1)中，已经从实验和理论上证明，金属材料不会发生损伤和破坏；在区间(2)、(3)中，金属材料主要发生剪切型损伤破坏；在区间(4)中，金属材料主要发生延性损伤破坏。

图12 应力三轴度对损伤模式转变的影响

上述分析可以看出，径厚比的不同主要改变了膨胀环变形后期的应力状态，进一步改变了微观损伤断裂机理。在中等厚度的战斗部中会出现拉伸和剪切混合破坏模式。

4 结 论

本文给出了基于修正B-W模型的材料碎裂本构关系，研究了战斗部爆炸破片形成机理，讨论了破坏模式变化规律。主要得到以下几点结论:

(1) 基于JC模型的流动应力准则和改进B-W模型的内聚力断裂准则可以有效模拟膨胀环碎裂过程。

(2) 膨胀环膨胀碎裂过程可以分为整体塑性阶段、稳定颈缩阶段、局部颈缩发展阶段和最终碎裂形成阶段；局部颈缩发展形成的Mott卸载波对邻近区域的应力卸载作用明显，抑制了邻近颈缩的进一步发展。

(3) 随着初始膨胀速度的增大，破片数量呈线性增加，且破片质量分布服从Rayleigh分布。

(4) 径厚比能显著影响碎裂机理，随着径厚比的增大，碎裂模式逐渐从延性颈缩失稳破坏，过渡到延性破坏与剪切破坏交替的混合破坏模式，并最终过渡到剪切带破坏；破坏模式改变的主要原因是膨胀环变形后期应力状态的差异。

[1] MOTT N F. Fragmentation of shell cases[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1947, 189: 300-308.

[2] SCHEFFLER D R, ZUKA J A. Practical aspects of numerical simulation of dynamic events: material interfaces[J]. International Journal of Impact Engineering, 2000, 24(8): 821-842.

[3] ZUKAS J A, SCHEFFLER D R. Practical aspects of numerical simulations of dynamic events: effects of meshing[J]. International Journal of Impact Engineering, 2000, 24(9): 925-945.

[4] GURSON A L. Plastic flow and fracture behavior of ductile meterials incorporating void nucleation,growth and interaction[D]. Brown University, 1975.

[5] JOHNSON G R, COOK W H. Fracture Characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21: 31-48.

[6] BAO Y, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81-98.

[7] BARSOUM I, FALESKOG J. Rupture mechanisms in combined tension and shear—Experiments[J]. International Journal of Solids and Structures, 2007, 44: 1768-1786.

[8] BARSOUM I, FALESKOG J F. Rupture mechanisms in combined tension and shear-Micromechanics[J]. International Journal of Solids and Structures, 2007, 44: 5481-5498.

[9] RUSINEK A, ZAERA R. Finite element simulation of steel ring fragmentation under radial expansion[J]. International Journal of Impact Engineering, 2007, 34(4): 799-822.

[10] ZHANG H, RAVI-CHANDAR K. On the dynamics of necking and fragmentation—II.Effect of material properties, geometrical constraints and absolute size[J]. Int J Fract, 2008, 150: 3-36.

[11] 陈磊，周风华，汤铁钢. 韧性金属圆环高速膨胀过程的有限元模拟[J]. 力学学报, 2011, 43(5): 861-870.

CHEN Lei, ZHOU Fenghua, TANG Tiegang. Finite element simulations of the high velocity expansion and fragmentation of ductile metallic rings[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(5): 861-870.

[12] 郑宇轩. 韧性材料的动态碎裂特性研究[D]. 合肥：中国科技大学, 2013.

[13] 郑宇轩，陈磊，胡时胜，等. 韧性材料冲击拉伸碎裂中的碎片尺寸分布规律[J]. 力学学报, 2013, 45(4): 580-587.

ZHENG Yuxuan, CHEN Lei, HU Shisheng, et al. Characteristics of fragment size distribution of ductile materials fragmentized under high strain rate tension[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 580-587.

[14] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperature[C]. Proceedings of the seventh international symposium on ballistics, Netherland, 1983.

[15] 李营. 液舱防爆炸破片侵彻作用机理研究[D]. 武汉:武汉理工大学, 2014.

[16] 郭子涛. 弹体入水特性及不同介质中金属靶的抗侵彻性能研究[D]. 哈尔滨:哈尔滨工业大学, 2012.

Blast fragments forming mechanism of a warhead based on modified BW model

LI Ying1,2, WU Weiguo1, DU Zhipeng2, ZHANG Wei2, ZHANG Chunhui2, ZHANG Lei1

(1. School of Transportation, Wuhan University of Technology, Wuhan, 430063, China;2. Naval Academy of Armament, Beijing 100161, China)

Expanding ring is a useful means to study a warhead’s blast fragments forming mechanism. Here, through introducing a modified BW cohesive force fracture model’s ABAQUS subroutine, the fragmentation process of an expanding ring was simulated numerically. The expanding fragmentation process was divided into four stages. The effects of expanding velocity on fragments’ mass distribution and fragments number were discussed. The effects of thickness on the fragmentation mode were also studied. It was shown that the fragmentation process is divided into 4 stages including overall plastic deformation, steady necking, local necking developing and fragmentation; the fragments number increases with increase in the initial expanding velocity and the mass distribution of fragments obeys Rayleigh distribution; the variation of the radius-thickness ratio changes stress status of end deformation stage, the stress of thin shell structures is mainly tensile, while the shear stress status appears in the end stage of thick shell structures, so their fracture modes transfer gradually from tension necking failure to shear failure.

anti-ship missile; expanding ring; blast fragmentation; Rayleigh distribution; stress tri-axiality

国防基础研究项目(B1420133057)；国家自然科学基金(51509196)；非线性力学国家重点实验室开放基金(LNM201505)；中央高校基本科研业务费专项资金(2014-YB-20)。

2016-03-10 修改稿收到日期：2016-06-14

李营 男，博士生，1988年生

O389；TJ410

A

10.13465/j.cnki.jvs.2017.15.018