热冲击下带裂纹功能梯度厚壁圆筒的分析
2017-08-30彭亦鹏陈爱军
彭亦鹏, 陈爱军
(南京理工大学 理学院,南京 210094)
热冲击下带裂纹功能梯度厚壁圆筒的分析
彭亦鹏, 陈爱军
(南京理工大学 理学院,南京 210094)
针对功能梯度材料热冲击下的断裂问题,对功能梯度材料的材料参数分类进行加权处理,建立带裂纹功能梯度厚壁圆筒的模型;给出热量平衡方程与边界条件,建立相关问题的有限元分析格式;改进Calahan算法以适用于带状稀疏矩阵的一阶非齐次常微分方程组,完善温度场的求解过程,计算了裂纹尖端的温度应力强度因子,并且分析功能梯度材料组分构成对温度应力强度因子的影响。以上研究为带裂纹功能梯度厚壁圆筒的可靠性分析及结构优化设计提供了参考。
功能梯度材料;厚壁圆筒;热冲击;温度应力强度因子;有限元分析;裂纹
功能梯度材料最早是作为热格栅提出的,故而此类结构在热环境中的响应分析一直是研究的重点。过去数年内,各国学者开展了大量的研究工作,Hui等[1]用无网格法对功能梯度材料进行了热力学分析;陈健桥等[2]将无网格Petrov-Galerkin方法应用于功能梯度材料的三维热传导问题;Shen等[3]分析了功能梯度材料板在热环境中和横向压力作用下的非线性弯曲;Sutradhar等[4]用边界元法分析了功能梯度材料的瞬态热传导问题;Sladek等[5]利用无网格局部边界元法,分析了功能梯度材料的瞬态热传导问题; Chen等[6]用精细积分法对功能梯度材料的热传导问题进行了灵敏度分析。Liu等[7]基于二维各向异性热弹性理论,给出了均匀热流下带裂纹功能梯度材料的应力强度因子的解决办法。Lee等[8]采用有限单元法分析了梯度板在热弹性加载下的非线性响应问题。田建辉等[9]采用混合数值法分析了功能梯度材料板中瞬态热响应问题。曹蕾蕾等[10]针对功能梯度材料物性参数随坐标变化的特点,基于Trefftz完备解提出了求解功能梯度材料热传导问题的有限梯度元方法。针对功能梯度材料的二维瞬态热传导问题,蓝林华等[11]提出了一种有效的降维精细积分法。李世荣等[12]基于Timoshenko梁理论研究了功能梯度材料梁在一维热冲击载荷作用下的瞬态动力响应。高效伟等[13]采用径向积分边界元法分析了功能梯度材料动态断裂力学问题。唐雪松[14]研究了含中心裂纹的正交各向异性板,在远场均匀热流作用下温度场的分布。Wang等[15]通过FE/FD方法计算了功能梯度材料的瞬态温度场和相关的热应力。赵军等[16]采用摄动法推导出无限大对称型梯度功能材料平板的一维非定常温度场及非定常热应力场的解析解,并计算了瞬态热应力强度因子。Zhang等[17]通过DQM对功能梯度壳在瞬态温度场中的热应力进行分析。同样采用DQM数值解法,蒲育等[18]得到了功能梯度梁自由振动的二维弹性解。杜长城等[19]研究了热环境中功能梯度圆柱壳的内共振非线性模态。
基于现有的文献的不足,本文首先希望能将关于功能梯度材料研究由解析解引入到试件的数值分析当中,建立一种相对自由的功能梯度厚壁圆筒力学性能参数函数,在此基础上的编写相应模块的程序。与此同时,参考了吕和祥等[20]对一阶齐次常微分方程组的解法,改进了Calahan算法,提供了一种行之有效的算法来计算有限元离散后的热冲击下功能梯度厚壁圆筒微分方程。
本文的研究首先建立功能梯度厚壁圆筒的微分方程;然后推导了改进的Calahan算法以求解一阶非齐次常微分方程;之后进行数值计算,通过计算热冲击下带裂纹功能梯度厚壁圆筒的温度应力强度因子,验证了算法的有效性与适用性;提出热冲击下带裂纹功能梯度厚壁圆筒相关问题的结论。
1 热冲击下功能梯度厚壁圆筒的微分方程
1.1 均匀材料瞬态热传导问题的微分方程
首先,瞬态温度场的温度变量φ在直角坐标系中应满足微分方程
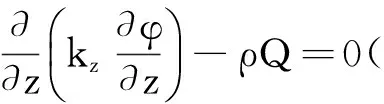
(1)
即热量平衡方程,式中的第一项是微体升温需要的热量;第2,3,4项是由x,y和z方向传入微体的热量;最后一项是微体内热源产生的热量。微分方程表明,微体升温所需的热量应与传入微体的热量以及微体内热源产生的热量相平衡。
边界条件如下:
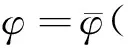
(2)
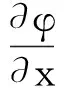
q(在Γ2边界上)
(3)
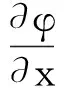
h(φa-φ)(在Γ3边界上)
(4)
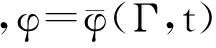
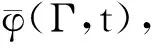
1.2 功能梯度厚壁圆筒的材料特性
对于如图1功能梯度厚壁圆筒模型的功能梯度厚壁圆筒,长度为L,中心半径为r,厚度为2h,建立坐标系(x,θ,z),其中,坐标原点于圆心,θ轴在圆周方向,z轴在圆筒中心方向。考虑圆筒的内表面承受热冲击载荷,外表面与环境做热对流的边界条件。
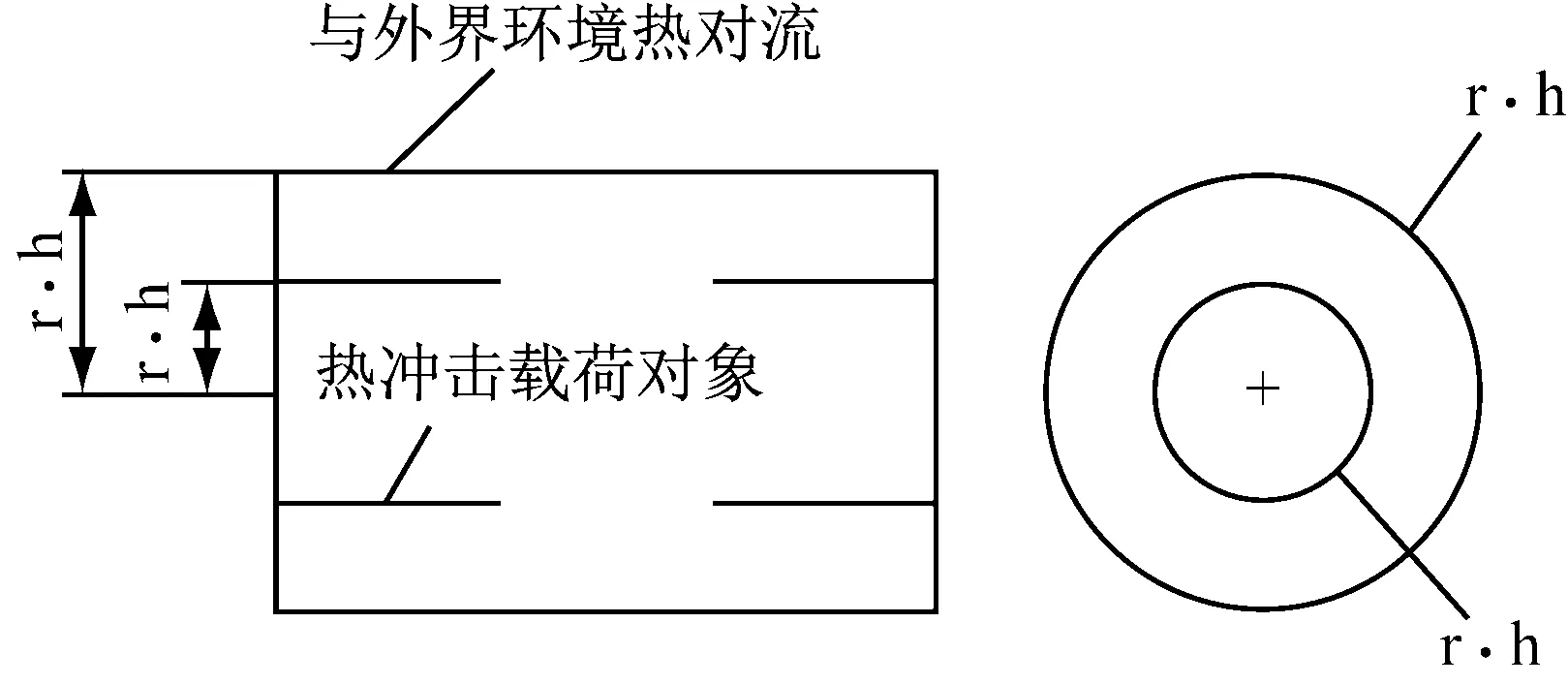
图1 功能梯度厚壁圆筒模型
复合材料的材料特性是用混合物的线性规则来描述的。引入参数c(x)∈[0,1]。基于图1给出的模型,可令
(5)
式中:x是半径,c0、k和n是材料参数。在式(5)的描述下,通过选取适当的n和k,可以实现功能梯度材料特性范围较大的非线性连续变化。
对于材料的温度特性,即热传导系数kx、kθ,比热容Cx、Cθ,密度ρx、ρθ,用P来表示。以两种材料为例,P可以表示为
P=Pic(r)+Pj[1-c(r)]
(6)
式中,Pi、Pj表示这两种材料的温度特性。
在小变形假设下,应变与位移的关系是

(7)
式中:u是径向位移;εx,εθ是应变。
依据混合物的线性规则以及两种线弹性材料的均匀假设,功能梯度厚壁圆筒的应力由下式给出
(8)
其中,
(9)
下标0,1表示两种不同的材料,λi、μi是拉梅系数。式(8)表示混合物的线性规则应用于拉梅系数得出的结果。
由Xin[21]可以得出,如此描述功能梯度材料的等效性能,对试件模型的计算精度有很大提升,也更加符合实际情况。
1.3 边界条件的形成
在如图1所示模型中,假设厚壁圆筒的外部与外界热传导,内部受到热冲击荷载。
温度的初始条件和外部、内部边界条件是
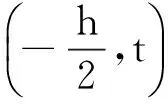
(10)
(11)
式中:ΔT是热载荷振幅;a是载荷变化的常数;hr是厚壁圆筒与外界的换热系数。
1.4 有限元格式的建立
由于功能梯度材料断裂问题十分复杂,从理论上给出问题的解析解耗时耗力,不具有通用的意义。而实际工程应用当中,功能梯度材料制备的多样性,使材料模型与荷载的形成各式各样,增加了理论分析的难度。通过运用有限单元法编写程序,求解功能梯度材料的断裂问题,能够在工程中得到广泛的应用。厚壁圆筒模型可以简化为平面问题,在程序的编写过程当中应用四边形八节点等参单元。
对于形如式(1)的微分方程,建立等效积分形式
(12)
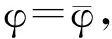
w=w2=w3=δφ
(13)
将式(13)代入式(12),并对其中第1个域Ω内积分的第2-4项进行分布积分,则可得到
(14)
利用式(12)可以建立瞬态温度场有限元的一般格式,首先将空间域Ω离散为有限个单元体,在典型单元内温度φ仍可以近似地用节点温度φi插值得到,但要注意此时的结点温度是时间的函数,即
(15)
插值函数Ni只是空间域的函数,应具有插值函数的基本性质,将式(15)代入式(14),并考虑到dφi的任意性,就可以得到用来确定n个结点温度φi的有限元求解方程
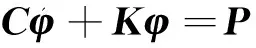
(16)
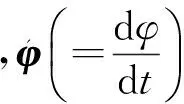
(17)

(18)
(19)
(20)
(21)
(22)
(23)
至此,已将时间域和空间域的偏微分问题在空间域内离散为N个结点温度φi(t)的常微分方程的初值问题,对于给定温度值的边界Γ1上n1个结点,方程组始终的相应项应引入的条件是
(24)
式中,i是Γ1上ni个结点的编号。
2 一阶非齐次常微分方程组具有三阶精度的无条件稳定的隐式算法
将式(6)所确定的材料系数代入式(16)中,可以得到以时间为变量的一阶非齐次常微分方程组
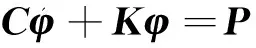
(25)
本节中提出一个新算法,使Calahan算法适用于矩阵K为稀疏带状矩阵,也就是对一般的非齐次常微分方程组提出一个具有三阶精度,无条件稳定自起步的算法,并且能够不破坏原稀疏矩阵的存储方式及其运算规则。
当C是非奇异矩阵时,可分解为
C=LU
(26)
其中L是下三角阵,U是上三角阵。当C是对称矩阵时U=LT。将式(26)代入式(25),并前乘L-1,同时令
ψ=Uφ
(27)
则方程(25)化为标准形式
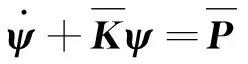
(28)
其中
(29)
2.1 自起步、三阶精度的逐步积分法
令ψ1=ψ(tk+f),ψ0=ψ(tk),由(28)有
(30)
其中,
(31)
将式(31)代入(29),有
(32)
由式(32)解出ψ1,有
(33)
调整T使得式(33)左端的系数为平方的形式,因此令
(34)
由式(34),可以求得
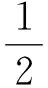
(35)
由式(35),式(34)变为
(36)
通过移项与化简,得到在原来带状阵上运算的递推公式
φ1=(C+fUK)-1C(C+fUK)-1×
(37)
式(37)所有的运算都可以在稀疏矩阵存储的方式上运行,其中所有的逆矩阵只是一个形式上的写法,因为所要求的并不是逆矩阵本身,而是它与列向量的乘积,即可以用稀疏矩阵和列向量想成运算规则,用解线性方程组的方法得到。
2.2 稳定性分析
把方程(37)用于单自由度方程

则有
x1=Hx0
(38)
其中
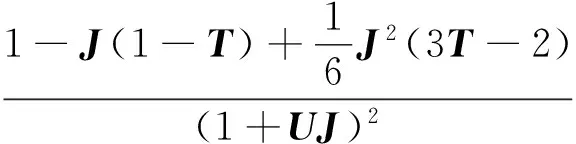
(39)
显然只有

(40)
由式(39)计算得

3 热冲击下带裂纹功能梯度厚壁圆筒的数值分析
3.1 应力强度因子
应力强度因子作为断裂力学的重要参量,其量纲是[力]×[长度]-3/2,是表征裂尖应力场强度的物理量,一般以符号K表示。由于非均质线弹性体裂纹尖端渐进场与均质线弹性体裂纹尖端渐进场相同,因此由裂纹应力强度因子与裂纹张开位移之间的关系可以得出应力强度因子的表达式,为
(41)

(42)
式(41)中,KI,KII和KIII分别称为Ⅰ型、Ⅱ型和Ⅲ型裂纹的应力强度因子,μtip为裂纹尖端剪切模量,r为裂纹面上考虑的点到裂纹尖端的距离,Δui(r),i=1,2,3为局部坐标系下裂纹张开位移,其表达式为
(43)
3.2 程序的设计
对于程序的设计,旨在通过有限元的工具,对模型进行计算,从而得出较为精确的结果。
首先是通过商业软件Ansys进行建模,划分网格。导出单元信息Elements.txt和单元信息Nodes.txt。模型不考虑机械荷载。Materials计算功能梯度材料中的材料参数,并编入与单元等容的数组中。Boundary TemperatureConditions用以输入温度边界条件,并离散为列阵。Ske和Stiff函数用以计算单元热传导矩阵与总体热传导矩阵。在单元刚度矩阵的计算中,通过InverseMatrix来计算Jacobi矩阵的逆阵。CaMatrix用以计算热容矩阵。在形成热容矩阵C,热传导矩阵K和温度载荷列阵P之后,用如Caption2的方法计算结点温度列阵φ。随后,设计Strain函数来计算结点应变,StressFactorsIntense函数以计算温度应力强度因子,输出为Result.txt。并用线性拟合方法进行后处理,并在Matlab得到图形形式的结果。程序设计框图,见图2。
3.3 温度场的计算
在下文中,考虑由SiC和Ni构成的功能梯度厚壁圆筒。成分的材料参数在表1中给出,泊松比为0.2。
在这一节中,功能梯度厚壁圆筒内部边界为全陶瓷,外部边界为全金属,组分比N1/N2=k,功能梯度厚壁圆筒的长度L=10 m,R=6 m,r=2 m。热冲击载荷为T0=300 K,ΔT=100 K以及a=10,热交换系数是hr=100。
使用ANSYS划分网格,网格与裂纹尖端显示于图3。图4中是功能梯度厚壁圆筒的内壁,外壁与中心的温度场。

表1 材料参数
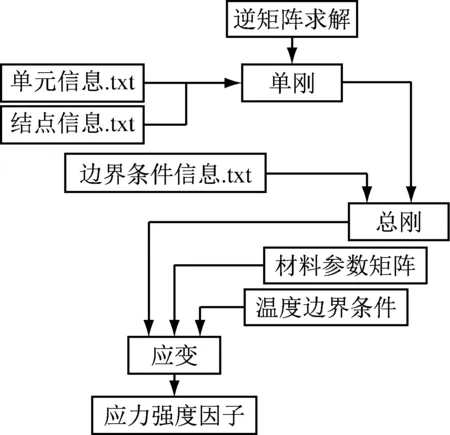
图2 程序框图
图3 模型网格
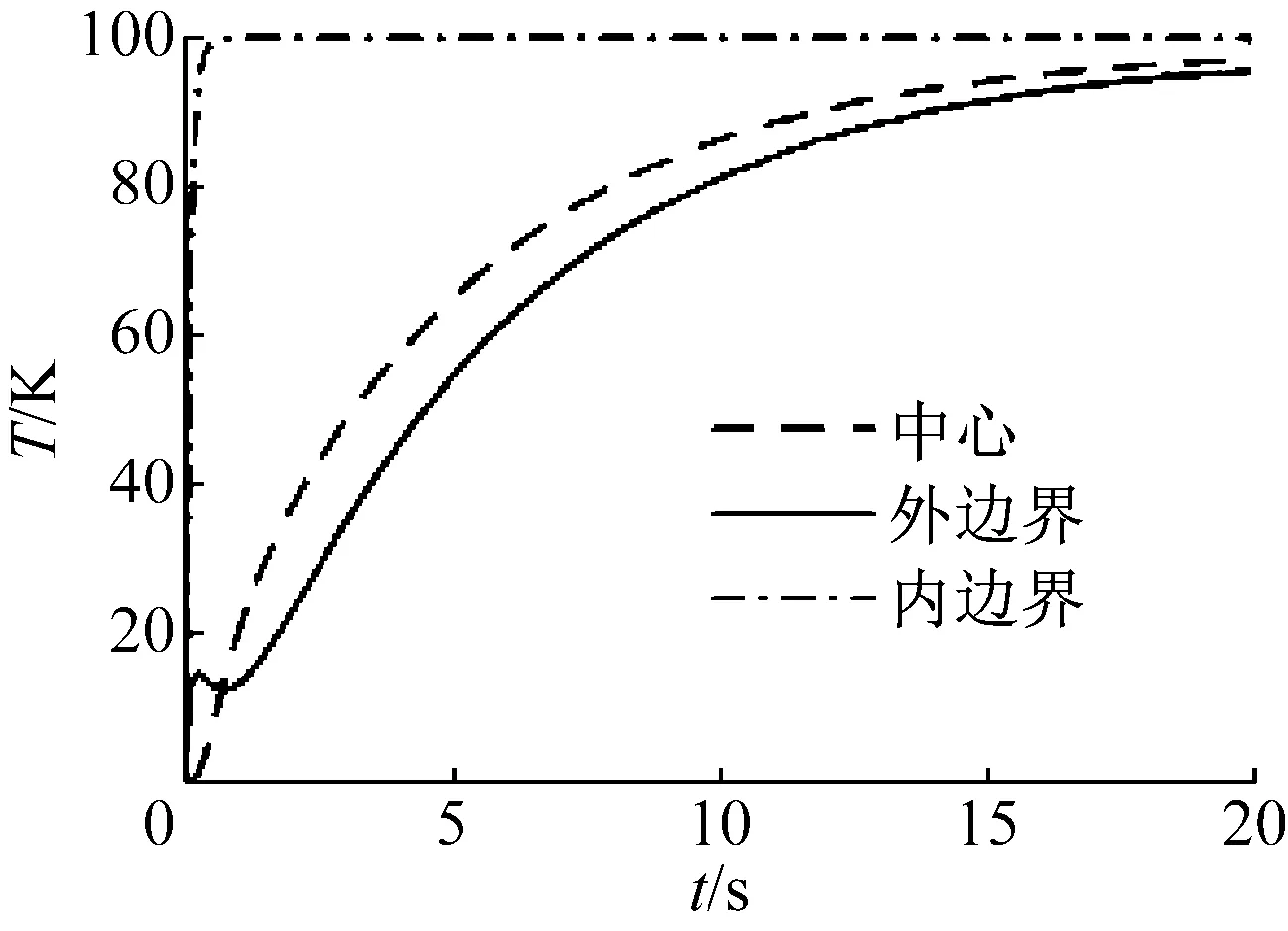
图4 功能梯度厚壁圆筒内壁、外壁与中心温度
显然,内壁温度随着热载荷而迅速增加。系统温度随响应时间而趋于稳态,这与李世荣等[12]的研究保持一致。
3.5 应力与应力强度因子的计算
由上节求得的温度场求得应变,依照弹性力学的本构关系进一步可以得到功能梯度厚壁圆筒的应力。
为了验证上一部分中改进的Calahan算法(Improved Calahan Method,ICM)的可靠性,先做一组对比分析。分析各向同性的均匀材料Cu作为厚壁圆筒材料,模型尺寸、温度荷载与上一节相同。
从图5和图6中可以看出,对于以Cu为材料的厚壁圆筒,ICM求得的结果与有限元分析软件Ansys得出的结果相近。当系统达到稳态后,误差在0.03%以内。改进的Calahan算法也将应用到接下来的计算中。
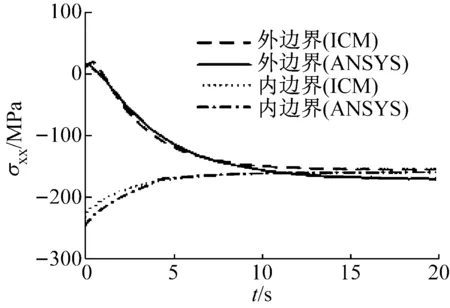
图5 Cu为材料的厚壁圆筒瞬态热应力σxx

图6 Cu为材料的厚壁圆筒瞬态热应力σθθ
图7和图8展示了上节所示的功能梯度厚壁圆筒的径向和切向应力。可以看出,随着厚壁圆筒的温度场趋于稳态,不同位置的应力也趋于定值。

图7 不同表面的瞬态热应力σxx
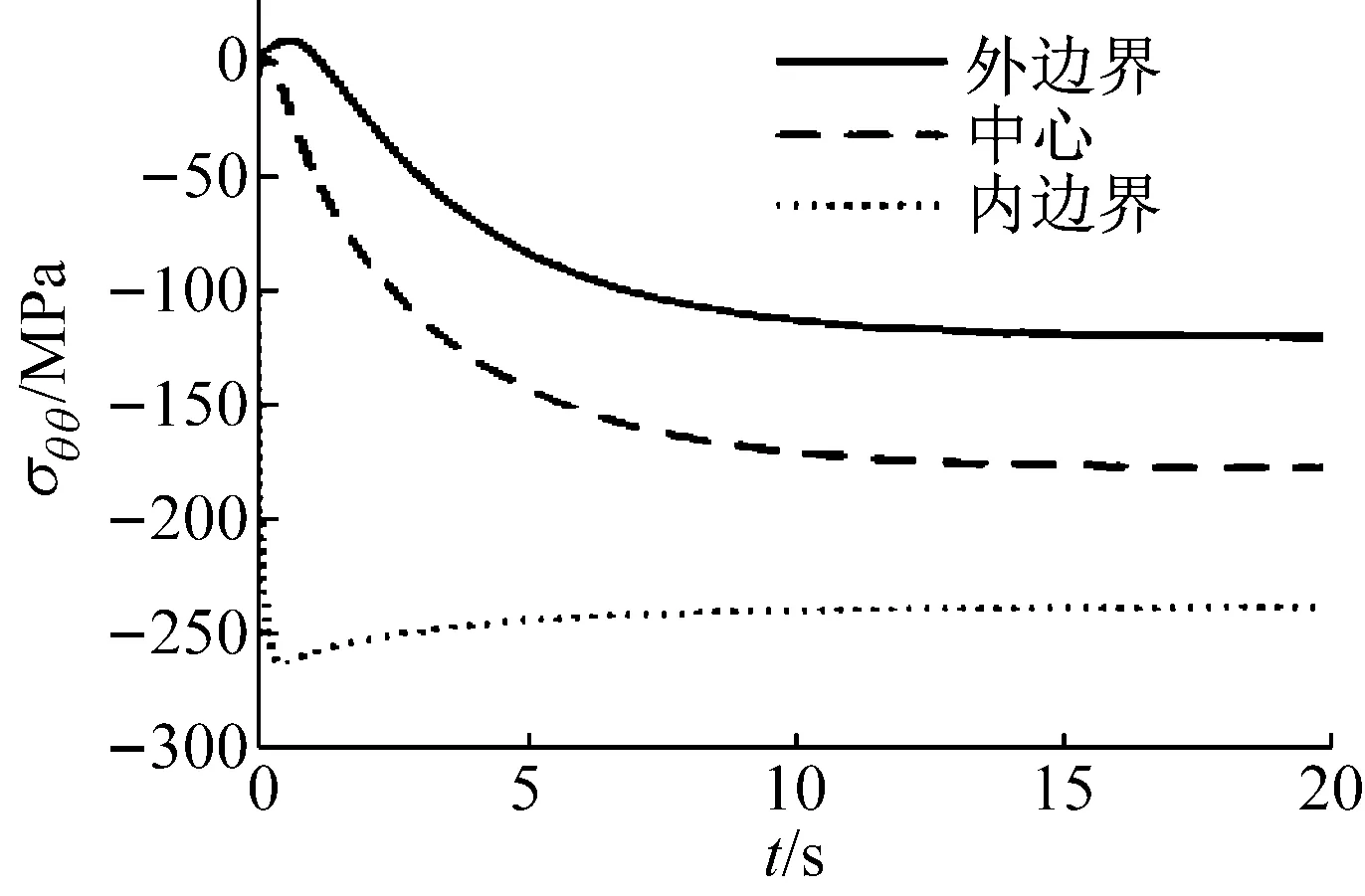
图8 不同表面的瞬态热应力σθθ
图9展示了在热载荷变化时候的裂纹尖端应力强度因子。
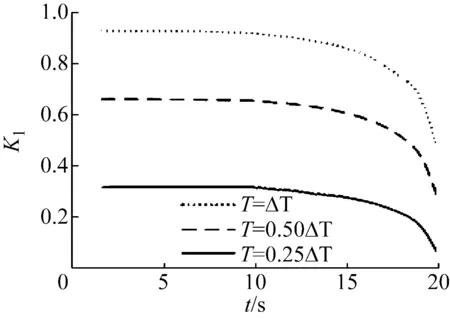
图9 T=0.25ΔT,0.5ΔT,ΔT时应力强度因子
在T=0.5ΔT时,变化式(5)中n的值,通过运算得到了不同组分下,温度应力强度因子随时间变化的结果展示于图10。

图10 不同组分下的温度应力强度因子
4 结 论
本文基于线弹性理论,对内壁受热冲击载荷的厚壁圆筒进行了分析。首先,基于微分方程等效积分形式的伽辽金提法在空间域进行有限元离散,得到一阶常微分方程组,并引入改进的Calahan算法进行温度场的求解。研究的主要结论是:
(1) 热应力随着热冲击激增,峰值热应力发生在功能梯度厚壁圆筒的内、外表面。与温度场不同的是,应力在不同表面收敛到不同的定值。
(2) 当功能梯度厚壁圆筒受到热冲击时,功能梯度材料组分连续变化的特性使其在很短的时间内缓和温度场的峰值。然而,当温度趋于稳定时,由于功能梯度材料不均匀的特性,残余环向应力仍较大。因此残余环向应力不能忽略。
(3) 随着热冲击温度的变化,即ΔT/T逐渐增大,温度应力强度因子依次变大,并逐渐趋于稳定,在达到稳定时比较接近。
(4) 组分变化对温度应力强度因子也有影响,随着组分变化,温度应力强度因子也随之变化。
[1] HUI W, QIN H Meshless approach for thermomechanical analysis of functionally graded materials[J]. Engineering Analysis with Boundary Elements, 2008, 32: 704-712.
[2] 陈健桥,丁亮.功能梯度材料瞬态热传导问题的MLPG方法[J]. 华中科技大学学报(自然科学版),2007, 35(4): 119-121.
CHEN Jianqiao, DING Liang, A MLPG method of transient heat transference in FGMs[J]. Journal of Huazhong University of Science and Technology(Nature Science), 2007, 35(4): 119-121.
[3] SHEN H S. Nonlinear bending response of functionally graded plates subjected to transverse loads and in thermal environments[J]International Journal of Mechanical Sciences 2002, 44: 561-584.
[4] SUTRADHAR A, PAULINO G H. The simple boundary element method for transient heat conduction in functionally graded materials[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193: 4511-4539.
[5] SLADEK J, SLADEK V, ZHANG C. Transient heat conduction analysis in functionally graded materials by the meshless local boundary integral equation method[J]. Computational Materials Science, 2003,28: 494-504.
[6] CHEN B S, TONG L Y. Sensitivity analysis of heat conduction for functionally graded materials[J]. Materials and Design, 2004,25: 663-672.
[7] LIU L, KARDOMATEAS G A. A dislocation approach for the thermal stress intensity factors of a crack in an infinite anisotropic medium under uniform heat flow[J]. Composites:Part A Appled Science and Manufacturing, 2006,37: 989-996.
[8] LEE S J, REDDY J N. Non-linear response of laminated composite plates under thermomechanical loading[J]. International Journal of Non-Linear Mechanics, 2005, 40(7): 971-985.
[9] 田建辉,韩旭,孙小卫. 基于混合数值法的功能梯度材料板瞬态热响应分析[J]. 固体力学学报, 2008,29(4): 396-401.
TIAN Jianhui, HAN Xu, SUN Xiaowei. Transient thermal response of functionally graded material plates based on the hybrid numerical method[J]. Chinese Journal of Solid Mechanics, 2008, 29(4): 396-401.
[10] 曹蕾蕾, 裴建中, 张春国,等. 基于混合Trefftz有限梯度元法的功能梯度材料热传导数值模拟[J]. 中国科技论文, 2015,10(2): 222-226.
CAO Leilei, PEI Jianzhong, ZHANG Chunguo, et al. A hybrid Trefftz graded finite element method to steady-state heat conduction in functionally graded materia[J]. China Sciencepaper, 2015,10(2): 222-226.
[11] 蓝林华,富明慧,程正阳.功能梯度材料瞬态热传导问题的降维精细积分法[J].固体力学学报,2010,31(4): 406-410.
LAN Linhua, FU Minghui, CHENG Zhengyang. Decrement-dimensional precise time integration of 2-D transient heat conduction equation for functionally graded materials[J]. Acta Mechanica Solida Sinica, 2010, 31(4): 406-410.
[12] 李世荣,范亮亮.功能梯度梁在热冲击下的动态响应[J].振动工程学报,2009, 22(4): 371-378.
LI Shirong, FAN Liangliang. Dynamic responses of functionally graded material beams under thermal shock[J]. Journal of Vibration Engineering, 2009, 22(4): 371-378.
[13] 高效伟, 郑保敬, 刘健. 功能梯度材料动态断裂力学的径向积分边界元法[J]. 力学学报, 2015, 47(5): 868-873.
GAO Xiaowei, ZHENG Baojing, LIU Jian. Dynamic fracture analysis of functionally graded materials by radial integration bem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015,47(5): 868-873.
[14] 唐雪松. 含中心裂纹正交各向异性板均匀热流作用下的温度场解析解[J]. 工程力学, 2007,24(3): 28-41.
TANG Xuesong. Analytical solutions of temperature fields for an orthotropic plate with a central crack under remote uniform heat flows[J]. Engineering Mechanics, 2007,24(3): 28-41.
[15] WANG B L, MAI Y W, ZHANG X H. Thermal shock resistance of functionally graded materials[J]. Acta Materialia, 2004,52: 4961-4973.
[16] 赵军, 王朝霞, 董一芬,等. 对称型梯度功能材料的瞬态热应力强度因子[J]. 山东大学学报(工学版), 2004, 34(3): 9-13.
ZHAO Jun, WANG Chaoxia, DONG Yifen, et al. Transient thermal stress intnsity factors for a functionally gradient material with symmetrical structure[J]. Journal of Shandong University(Engineering Science), 2004, 34(3): 9-13.
[17] ZHANG J H, LI G Z, LI S R, et al. DQM based thermal stresses analysis of a functionally graded cylindrical shell under thermal shock[J]. Journal of Thermal Stresses, 2015, 38(9): 959-982.
[18] 蒲育,滕兆春.Winkler-Pasternak弹性地基FGM梁自由振动二维弹性解[J]. 振动与冲击, 2015, 34(20): 74-79.
PU Yu, TENG Zhaochun. Two-dimensional elasticity solutions for free vibration of FGM beams resting on Winkler-Pasternak elastic foundations[J]. Journal of Vibration and Shock, 2015, 34(20): 74-79.
[19] 杜长城,李映辉,金学松.热环境中功能梯度圆柱壳的内共振非线性模态[J]. 振动与冲击, 2014, 33(6): 161-165.
DU Changcheng, LI Yinghui, JIN Xuesong. Nonlinear normal modes of functionally graded cylindrical shells with internal resonance in thermal environment[J]. Journal of Vibration and Shock, 2014, 33(6): 161-165.
[20] 吕和祥,董志强,陈建峰. 一阶常微分方程组的一个有效解法[J]. 大连理工大学学报, 2006, 46(5): 629-632.
LÜ Hexiang, DONG Zhiqiang, CHEN Jianfeng. Effective solution method for the first-order ordinary differential equation system[J]. Journal of dalian university of Technology, 2006, 46(5): 629-632.
[21] XIN L B, DUI G S, YANG S Y, et al. An elasticity solution for functionally graded thick-walled tube subjected to internal pressure[J]. International Journal of Mechanical Sciences, 2014(89): 334-349.
Numerical simulation for a functionally graded thick-walled cylinder with cracks under thermal shock
PENG Yipeng, CHEN Aijun
(School of Sciences, Nanjing University of Science & Technology, Nanjing 210094, China)
Aiming at the fracture problem of functionally graded materials under thermal shock, physical parameters of functionally graded materials were classified and weighted to establish a model of a functionally graded thick-walled cylinder with cracks. Its heat balance equations and boundary conditions were deduced to build the relevant problem’s finite element analysis procedure. Calahan algorithm was improved to solve the first order inhomogeneous ordinary differential equations of the corresponding banded sparse matrix and obtain the cylinder’s temperature field and stress field. Then the thermal stress intensity factor of the crack tip was calculated, the effects of functionally graded material’s components on the thermal stress intensity factor were analyzed. The results provided a reference for reliability analysis and structural optimal design of a functionally graded thick-walled cylinder with cracks under thermal shock.
functionally graded materials; thick-walled cylinder; thermal shock; thermal stress intensity factor; finite element analysis; crack
江苏省自然科学基金(BK20150766)
2016-02-19 修改稿收到日期:2016-06-11
彭亦鹏 男,硕士生,1991年3月生
陈爱军 男,博士,副教授,1972年12月生
O316
A
10.13465/j.cnki.jvs.2017.15.010
