轨道交通制动气控集成板平面度非接触式测量研究

张嘉，谢建刚，陈国英，张磊

（中国铁道科学研究院机车车辆研究所，北京 100081）

轨道交通制动气控集成板平面度非接触式测量研究

张嘉，谢建刚，陈国英，张磊

（中国铁道科学研究院机车车辆研究所，北京 100081）

基于影像测量仪的非接触式图像测量原理，测量了轨道交通车辆制动系统关键子部件——气控集成板的表面点坐标。基于最小二乘法原理，建立了以测量点坐标为输入参数的平面度计算模型。对点坐标测量结果的统计分析发现，坐标偏差符合正态分布。利用蒙特卡洛方法对影像测量仪测量平面度进行了不确定度评定，该方法具有通用性，可推广到其他几何误差的不确定度评定。

非接触测量；气控集成板；测量不确定度

气控集成板是轨道交通车辆制动系统的关键零部件之一，当其表面几何误差较大时，易导致气控阀密封能力减弱、动作卡滞等故障，甚至造成行车安全隐患。因此，对于气控集成板表面几何误差（如平面度等）必须进行严格控制。

崔长彩等利用智能优化算法实现了平面度的误差评定，并针对既有文献数据进行了计算，其计算精度要高于最小二乘法。罗钧等利用牵引蜂和禁忌搜索技术改进了人工蜂群（ABC）算法，形成了MABC算法。目前，最小二乘法仍然是目前兼具适用性、稳定性的主流方法之一，有多位学者进行了研究和实际应用。

近年非接触式测量技术逐渐被应用到工业零件检测中。影像测量是基于光学成像原理，将被测要素的影像转化为数字信号，通过图像识别计算被测要素几何信息的非接触式测量方法，具有效率高、测量连续性强、采样点数多等优点，具有较大的发展潜力。

目前针对表面平面度的非接触式测量还缺乏具有针对性的不确定度评定研究。对于几何误差的不确定度评价，主流方法仍基于不确定度的标准评定规则。该方法对构成不确定度各分量分别评定，合成后得到不确定度。该方法要求分量解析表达，否则评定就难以进行。为解决该问题，可使用随机模拟方法——蒙特卡洛方法，该方法通过构造概率过程、计算机随机抽样、建立相关统计量三个过程完成求解。与经典的确定性方法相比，蒙特卡洛方法适用于难以直接解析描述或数值计算的问题，也适用于测量不确定度的评定。

本文建立了基于最小二乘法的平面度计算模型，用影像测量仪测量了制动系统气控集成板表面点坐标，并将测量结果应用到计算模型中，得出了表面平面度。根据蒙特卡洛方法原理编制了计算软件，并结合影像测量仪的计量特性，对平面度的测量进行了不确定度的评定。

1 基于最小二乘法的平面度计算模型

1.1 平面度计算模型的建立

以最小二乘平面作为评定基准，通过计算所有被测点与该评定基准面之间的距离得出平面度。该方法算法过程清晰明确，可操作性强，是计算平面度的基本算法。

设被测平面上的测量点坐标为Pi(xi,yi,zi)，设最小二乘平面方程：z =Ax+By+D（1）

其中，A、B、D分别为变换后的平面方程参数，x、y、z分别为三个方向上的坐标。

则根据最小二乘拟合理论，拟合的平面方程应满足拟合方程残差平方和最小，该目标函数设为F，

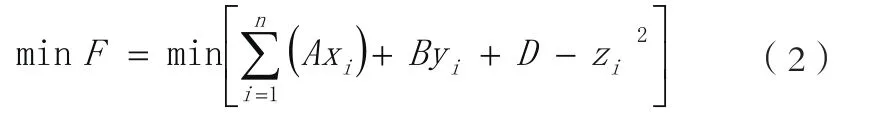
其中，xi、yi、zi分别是点i三个方向上的坐标值。

根据最小二乘理论，式(2)的必要条件是对各变量的偏导数为0，

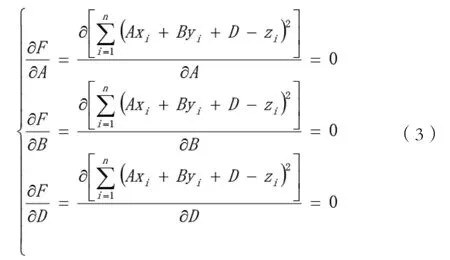
将方程组(3)整理可得关于平面方程三参数A、B、D的线性方程组，由于该方程阶数较少，结构简单，可以直接使用线性方程组解析解的形式求解计算。

平面度的计算如公式

表1 气控集成板表面点坐标（Z）手动测量和自动测量结果的假设检验

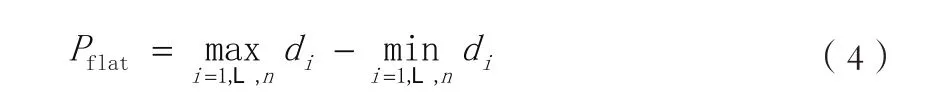
其中，Pflat是平面度；di是第i个测量点到最小二乘平面的距离，测量点位于朝向最小二乘平面法向量方向时为正，否则为负；n为测量点数。

1.2 平面度计算模型在气控集成板表面平面度测量中的应用

采用影像测量仪对气控集成板表面点进行测量，有手动和自动两种模式。由于自动测量模式完全是测量程序自动分析判断，因此聚焦范围、聚焦时间等参数都要大于手动模式。

构造假设检验，基于判断125组坐标测量结果（25个点每点测量5次），分析两种测量模式下的统计差异。如表1所示，当显著性水平为5%时，两种测量模式都符合正态分布，且在统计意义上并无差异，为便于研究和试验，本文采用自动测量模式。

根据假设检验理论，气控集成板表面点Z坐标实测结果的分布通过了显著性水平为5%时的Kolmogorov-Smirnov正态性检验。因此，对于同一点多次影像测量得到的坐标值偏差分布符合均值为0、标准差为0．00143的正态分布，即N(0, 0．001432)。

如图 1所示，根据最小二乘法拟合平面和平面度的基本定义，最小二乘拟合平面（定义为α）的平行平面中，能够包含所有表面测量点的最小间距即为平面度。满足该要求的两个平行平面分别以αU和αL表示，其距离为平面度Pflat。

图2显示了气控集成板安装面各测量点与最小二乘拟合平面α距离的分布，集成板绝大部分位置都接近于拟合平面α，即到平面α的距离≤0．015mm。仅左下局部角部分与拟合平面距离较大，这是该集成板在强度试验过程中局部装配紧固力矩过大和承载过重所致。

2 基于蒙特卡洛方法的平面度不确定度评定

采用蒙特卡洛方法进行测量不确定度的评定流程如图 3所示。首先，根据所需保留的有效数字位数计算抽样次数。其次，视频测量仪实测总结的分布特性，对N个测量点进行抽样，每个测量点产生M个符合预定分布特性的点坐标，并根据式(3)、(4)计算平面度等参数。上述过程迭代直至收敛，输出真值包含区间，完成不确定度评定。根据该流程使用Python语言编制了计算机软件执行不确定度评定。

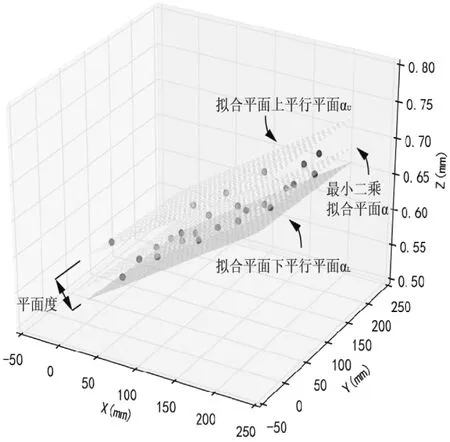
图1 气控集成板安装面25个测量点构建的最小二乘拟合平面及平面度

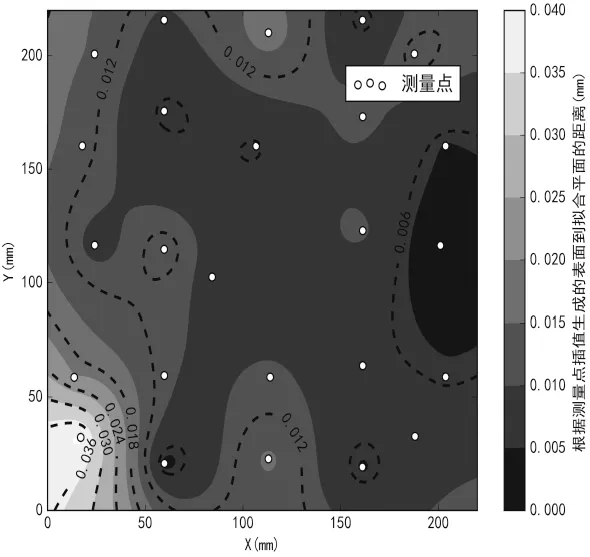
图2 气控集成板安装面25个测量点与最小二乘拟合平面距离分布

将影像测量仪测量的表面点坐标分布特性作为输入，按图 3的流程进行计算，即可得到蒙特卡洛方法评定结果。根据测量结果，本文研究的气控集成板表面平面度为0．061mm，当显著性水平为5%时，蒙特卡洛方法编制计算程序后计算出的真值包含区间为[0．057, 0．065](mm)。

3 结语

本文研究了影像测量仪测量轨道交通制动系统关键部件——气控集成板表面的平面度，基于最小二乘拟合法建立了平面度计算模型。采用蒙特卡洛方法对平面度测量结果进行了评定，并得出了真值包含区间。研究表明，该方法不仅适合影像测量仪测量平面度的不确定度评定，还可以推广到其他几何误差测量不确定度的评定过程。

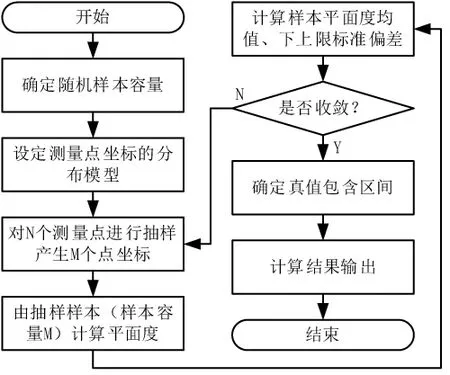
图3 平面度不确定度的蒙特卡洛方法评定计算流程

[1]崔长彩，张耕培，傅师伟，等．利用粒子群优化算法的平面度误差评定[J]． 华侨大学学报（自然科学版）, 2008, 29(4): 508-509．

[2]罗钧, 王强, 付丽． 改进蜂群算法在平面度误差评定中的应用．光学精密工程, 2012, 20(4): 427-428．

[3]温秀兰, 宋爱国． 改进遗传算法及其在平面度误差评定中的应用． 应用科学学报, 2003(3): 221-224．

[4]王志坚, 肖魁． 用最小二乘法求解平面度误差． 新疆工学院学报． 1994, 15(1): 43-45．

[5]王金星, 蒋向前, 马利民, 徐振高, 李柱． 平面度坐标测量的不确定度计算． 中国机械工程, 2005, 16(19): 1701-1703．

[6]Vladan Radlovac^ki, etc． Evaluating minimum zone flatness error using new method—Bundle of plains through one point． Precision Engineering． 2016, 43: 554-562．

[7]Christian P．Robert George Casella． Monte Carlo Statistical Methods 2ed． Springer, 2004: 83-90．

P258

A

1671-0711（2017）08（下）-0070-03