基于ARIMA模型下我国政府卫生支出的预测分析

2017-08-30

金融经济 2017年14期

(广西大学商学院，广西南宁 530004)

蔡雪月

(广西大学商学院，广西南宁 530004)

本文基于1990——2014年我国政府卫生支出的时间序列数据，通过建立合理地差分自回归移动平均模型进行拟合检验，描述了我国政府及卫生行政部门的卫生支出水平的基本走势，并对未来情况作出了预测分析。结果表明，ARIMA(1，1，0)模型能够为我国的政府卫生支出费用提供较好的预测，并且模型反映出政府在卫生领域的投入水平呈现逐年增长的趋势，且支出比重陡增。

ARIMA模型；政府卫生支出；时间序列分析；趋势分析

一、引言及文献简评

随着社会经济的快速发展，卫生事业的逐步深入，人民生活水平的日渐提高，越来越多的人们更加关注医疗卫生服务的质量，而在医疗卫生系统的建设中，国家政府的投入与支持很大程度上会影响我国的医疗服务水平。研究表明，近年来我国政府的医疗卫生支出效率达到了较好的水平，并且政府卫生支出比重是各级医疗机构产出效率的重要影响因素之一，同时也是对基层医疗机构效率影响较大的原因[1]。为保障医疗卫生体系建设的有效推进，很有必要对我国政府卫生经济的支出方面作科学性的分析。

一方面，基于现有数据若能对卫生资源发展水平进行较好地预测分析，这将更有意义。相关研究领域已经出现了不少具有代表性的学术文献，并且研究方法丰富多样，例如王莹(2015)采用定量与定性的方法对我国医疗机构床位资源配置进行预测研究[2]。李卫平等(2015)基于灰色预测模型评测了湖北省医疗机构的床位数[3]。黄二丹等(2013)探索了医疗机构床位需求量预测方法及应用，研究结果表明利用卫生资源人口比值法时预测效果最好[4]。王书平等(2015)通过趋势外推法和数据对比分析法预测了中国大陆2020年床位数结构情况[5]。此外，关于卫生经济领域的时间序列数据，更为常见的一些分析方法有ARMA模型、ARIMA模型、VAR模型、灰色预测或者干预分析模型方法等。如廖宇航等(2014)选取了能够衡量一个国家或地区在卫生事业投入水平的指标之一即人均卫生费用，建立了ARMA(3，2，2)模型，验证了海南省人均卫生费用逐年增长，并建议相关卫生行政部门应合理控制卫生费用的增长[6]。李莉等(2015)在生物统计领域，通过SPSS用自回归移动平均ARIMA模型拟合了2004——2013年甘肃省梅毒发病数[7]。杨立、常巍(2009)在对中国GDP数据建立的ARIMA模型基础上，进一步结合干预分析模型修正金融危机变故所引起的误差，同时也说明了干预分析模型可以很大程度上减小ARIMA模型的误差[8]。毛强等(2016)在“十三五”的背景下，分别对比分析所建立的灰色预测模型GM(1，1)和差分自回归移动平均模型ARIMA(2，2，1)，得出甘肃省在未来也将继续保持每千人口医疗卫生机构床位数需求量的不断上涨[9]。

另一方面，现今国家卫生投入实现了跨越式增长，据财政部最新消息报道，2016年全国财政医疗卫生支出达1.32万亿元，相比2015年增长了近10%，政府医疗卫生支出占财政支出的比重，提高到7.0%，这也是医改启动前即2008年的4.1倍。而关于我国政府卫生支出的相关研究丰富多样，我国实施医改政策之前，卫生医疗问题不断显露，在这样的时代背景下曹璐(2007)将政府卫生支出规模作为解决问题的切入点，合理界定了政府职责与卫生支出范围，并指出政府应适当扩大卫生支出规模[10]。新医疗改革实施后，我国政府更加关注医疗卫生事业的建设问题，李治(2012)重新对我国政府卫生支出规模指标进行趋势分析[11]。杨立群(2011)则在系统分析我国政府卫生支出规模与结构变化的基础上，通过面板数据回归模型揭示了卫生支出的影响因素，发现国内生产总值是主要影响因素[12]。梁学平(2013)通过对比分析国际情况得出我国医疗卫生政府支出水平偏低，与世界平均水平相比较仍然存在较大差距[13]。韩华为等(2010)、李郁芳等(2015)都对地方政府卫生支出进行效率核算，基于面板数据分别采用DEA-Tobit模型和数据包络分析方法发现样本区间内政府卫生支出效率有明显的地区差异，并且能够影响效率的因素主要包括医疗卫生改革政策、经济发展水平、财政分权、城镇化水平等[14-15]。

综上，本文立足于卫生经济的宏观层面，从时间发展角度出发，根据我国政府近二十多年的卫生支出水平的时间序列数据，建立单一变量的ARIMA模型拟合并预测卫生投入水平的未来走势，定量分析未来政府卫生支出的预测值，以期能对相关部门起到预测与建议的作用。

二、模型构建与研究设计

(一)理论模型介绍

ARMA(p,q)模型和ARIMA(p,d,q)模型是时间序列中两种最为常用的线性时间序列模型，而ARIMA模型事实上就是ARMA模型与差分运算相结合的组合模型[16]，全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model，简记ARIMA)，由博克思(Box)和詹金斯(Jenkins)共同提出，故又被称作box-jenkins模型博克思-詹金斯法。其中ARIMA(p，d，q)称为差分自回归移动平均模型，该模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高，是应用比较广泛的方法之一。赵肖肖等(2012)在SAS的平台下，同时引入方差检验法，对ARIMA模型的建模算法做了详细说明，并对CPI走势和预测做出科学的实证分析[17]。对于时间序列{xt}，建立求和自回归移动平均模型ARIMA(p,d,q)模型的结构如下：

其中，d表示序列{xt}经过d次差分运算以后，变为平稳序列，记为{▽dxt}；且假设此时满足ARMA(p,q)模型，该模型包含AR(p)模型和MA(q)模型两部分，AR(p)表示p阶自回归模型，MA(q)即为移动平均模型，{εt}为白噪声序列。具体形式为φ(B)▽dxt=θ(B)εt，或φ(B)(1-B)dxt=θ(B)εt，且φ(B)=1-φ1B-φ2B2-L-φpBp，θ(B)=1-θ1B-θ2B2-L-θqBq。

(二)概念模型框架图的构建

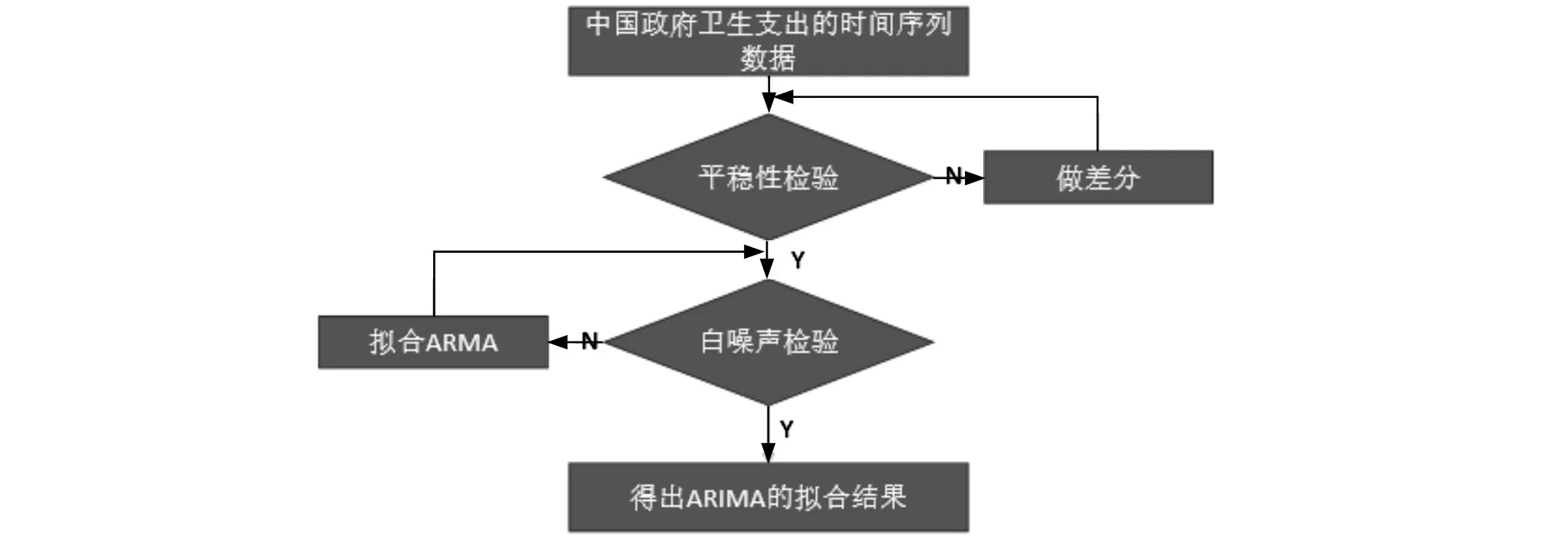
图1 概念模型框架图

本研究试图根据我国近二十余年政府卫生支出水平的时间序列数据，通过SPSS建立单一变量的差分自回归移动平均模型(ARIMA模型)并进行拟合，以期得到来自政府支持的医疗投入走势和统计规律，进而利用该模型预测序列未来的变化趋势。

三、实证结果分析

(一)数据来源与处理

本文研究所需数据全部来源于《中国卫生统计年鉴(2003—2013)》和《中国卫生和计划生育统计年鉴(2014—2015)》，通过对中国1990—2014年的政府卫生支出水平，由于政府卫生支出的原始数据是以当年物价水平衡量的，为了避免数据的剧烈波动，消除可能存在的异方差，所以对原始数据处理时先取对数，从而保证时间序列的平稳性。

为了更直观地观察1990—2014年来我国政府卫生支出的变化趋势，对原始数据做时序图，如图2所示，该时间序列呈现出明显的上升趋势，且从2006年起政府卫生支出显现出陡然增加的态势，2014年的全国投入量超过1万亿元。

从图2还可以看出，序列没有明显的季节成分，但却存在一个明显的变化走向，因此没有必要做季节分解。然而，ARIMA模型要求序列是平稳序列，因此需要对数据进行进一步的平稳性分析。

图2 中国1990——2014年政府卫生支出时序图

(二)序列平稳性处理及模型识别

经过一阶差分处理后的序列，通过平稳性检验，即d=1。再对一阶差分后的平稳序列分别检验其自相关函数(ACF)和偏自相关函数(PACF)，检验结果如图3所示，显然，自相关函数具有显著的拖尾性质，因此可以进一步确定模型ARIMA(p,d,q)中参数的取值。

图3 自相关图(左)与偏自相关图(右)

(三)模型的参数估计及检验：

根据一阶差分处理后的自相关图(图3左)和偏自相关图(图3右)初步确定参数取值为p=1,4;q=0，在经过SPSS软件的科学建模和多次拟合的尝试，确定最优模型为ARIMA(1，1，0)，此时R2的值为0.992非常接近于1，说明模型能够较好的对实际序列的波动进行拟合，模型ARIMA(1,1,0)具体拟合参数如表1所示。

表1 ARIMA模型参数

由表1可知，关于政府卫生支出的单一变量一阶差分的自回归移动平均模型的方程表达式即为：lnyt=0.163+0.475lnyt-1+εt。由回归方程可知，每一期的政府卫生支出水平都会受到滞后一期的支出影响，且正向相关。

进而对该模型的残差序列进行白噪声检验，具体检验结果如图5所示。显然，其残差序列自相关函数和偏自相关函数均在置信区间内，且P值小于0.5，说明差异没有统计学意义。因此，模型的残差序列为白噪声，模型拟合结果合理有效，因此可以进一步用于预测分析。

图4 残差序列的自相关图与偏自相关图

(四)模型预测

由模型的参数估计可知，p=1、d=1以及q=0时的ARIMA模型能够得出包含预测值、残差、标准误、置信区间以及百分比误差的序列，如图6即为我国政府卫生支出的趋势拟合图。

图5 政府卫生支出趋势拟合图

从图中可以发现，拟合值绘制的预测值序列检验模型，其在验证区间的性能极好，均至于置信区间内部，结果显示，对于1990年——2014年的全国政府卫生支出数量的拟合值及其95%可信区间的动态趋势，基本与政府的实际卫生支出额表现一致。因此，本研究可以用其作为模型的拟合点，进而对中国2017年的政府卫生支出数额进行预测。若与现有数据做对比，则经该模型的预测估计得2015——2017连续三年内我国政府卫生支出仍会继续加大投入量，并且全年支出金额均将超出1万亿元，但支出增加的额度会有轻微差异，2017的支出金额最终模型估计的2017具体数值约为1.373万亿元。

四、结论及启示

经实证检验，ARIMA(1,1,0)模型不仅能够将实际样本数据较好的拟合，并且预测到2017年中国政府卫生支出约为1.373万亿元，自1990——2014年一直呈现为增长趋势，尤其是在2006年开始出现转势，增长趋势变得更加迅猛。这表明我国为建立健全全民医疗保障制度，又因需要确保和推进医改的顺利实施，因此国家财政每年不断加大医疗卫生投入。然而，医疗卫生系统的建设与投入是方方面面的，具体而言政府医疗支出需用于全民医疗保障制度的建成、基本药物制度的建成、创新体制机制的形成、政策改革推进过程的资金支持、推动建立疾病应急救助制度、建立补偿机制的资金投入、基本公共卫生服务的公平化均等化体系标准的提高、基层医疗卫生服务体系建立健全的大量投资以及公立医院改革所需的资本投入等等。此外，政府医疗支出的多少很大程度上取决于国家财力水平，为顺应国家加大政府医疗支出的趋势，首当其要的是确保国民经济的综合实力不断增强。

然而，本研究仅仅是依据中国政府医疗支出跨度25年的时间序列数据进行预测，仍然存在一定的偏差，具有一定的局限性，可以通过更深入的研究改正，主要体现在以下几个方面：(1)由于是根据历史数据做推测，故随着预测年份的增加，不可预知的变故因素增加，误差可能会更大。因此，该预测结果定会与实际情况存在误差，若要在实际应用预测模型，还需进一步用更新的数据进行模型修正，以期提高模型的预测精度。(2)模型检验所引用的样本数据，其统计口径都是按照当年物价水平记录的，并且衡量政府医疗支出的标准为具体金额数目，而占比当年总支出的比重却无法核对。

[1] 屠彦.我国政府医疗卫生支出效率及其影响因素研究 [J].财会月刊，2015(33)：69-73.

[2] 王莹. 医疗机构床位资源配置的预测研究[D]. 北京中医药大学，2015：32-48.

[3] 王莹，李卫平. 灰色预测模型在湖北省医疗机构床位资源预测中的应用[J]. 医学与社会，2015(6)：57-59.

[4] 王书平，陈云香，黄二丹. 医疗机构床位需求量预测方法的应用及分析[J]. 卫生经济研究，2013(10)：32-35.

[5] 王书平，王耀羚，黄二丹. 中国2020年床位数医疗资源结构分析研究[J]. 中国卫生资源，2015(3)：160-162.

[6] 廖宇航，黄小玲，罗丽娟，等. 海南省人均卫生费用的自回归移动平均模型研究[J]. 中国卫生资源，2014(5)：349-350.

[7] 甘肃省疾病预防控制中心性病艾滋病科. ARIMA模型在预测甘肃省梅毒月发病情况中的应用[J]. 中国皮肤性病学杂志，2015(2)：160-163.

[8] 杨立，常巍. 干预分析模型在中国GDP预测中的应用[J]. 经济研究导刊，2009(1)：7-8.

[9] 毛强，刘兴荣. 甘肃省每千人口医疗卫生机构床位需求预测分析[J]. 中国初级卫生保健，2016(11)：1-3.

[10] 曹璐. 我国政府卫生支出规模研究[D]. 东北财经大学，2007：34-50.

[11] 李治. 我国政府卫生支出规模研究[J]. 西部财会，2012(10)：64-66.

[12] 杨立群. 我国政府卫生支出及影响因素与预测研究[D]. 北京协和医学院，2011：19-45.