数学整体性教学设计举隅
2017-08-28汪洪潮
汪洪潮
【摘 要】 数学知识有着内在的逻辑关系,课堂教学要抓住知识间的内在联系,整体把握知识结构,加强学生思维的整体性训练,培养学生的整体观念.掌握研究数学对象的基本套路和基本方法,提高系统思维水平.
【关键词】 整体性;基本套路;基本方法
近年来,“数学教学的整体性”越来越受到重视.人民教育出版社章建跃博士在《注重数学的整体性,提高系统思维水平》一文中指出,数学课堂教学要“注重数学的整体性”,“强调知识的逻辑连贯性”,加强对“数学学习理论和思考方法”的指导.但在实际教学中,这种知识和方法的“整体性”要求与具体的课堂教学往往存在着矛盾.实现二者的统一是广大教师努力追求的目标.如何在一堂课、一节内容中实现“数学的整体性”要求呢?现以教学中的几个案例进行说明.
1 抓住知识的内在联系,立足对知识的整体把握
数学知识有着内在的逻辑关系,课堂教学要抓住知识间的内在联系,帮助学生整体构建知识框架,培养学生的整体观念.以下是沪科版八年级下册《一元二次方程解法复习课》的教学片断:
老师:本节我们学习了一元二次方程的概念及其解法,在此之前我们学习了哪些和方程有关的知识?
学生:我们学习了一元一次方程、二元一次方程组、分式方程的概念及其解法.
老师:解这些方程的基本思路是什么?理论依据是什么?
学生:将二元转化为一元、将分式方程转化为整式方程,并最终将方程转化为x=a的形式.主要依据是等式的性质、运算律和合并同类项法则.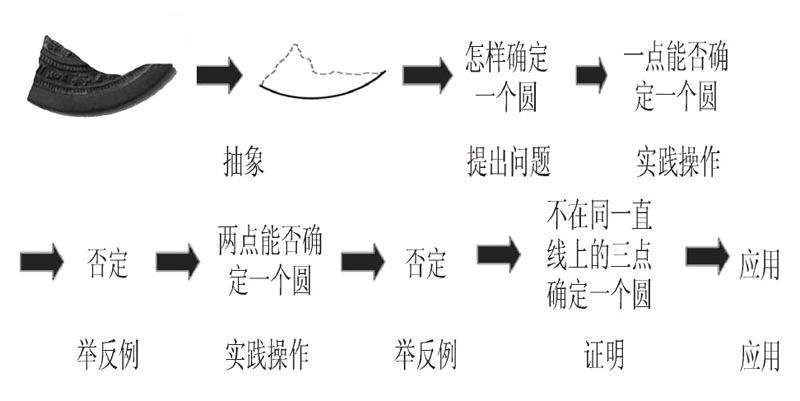
老师:解一元二次方程的基本思路是什么?
学生:将“二次”降为“一次”,即将一元二次方程ax2+bx+c=0转化为x=a的形式.
老师:最初是如何实现的?能举个例子吗?
学生:根据平方根的定义,用“直接开平方法”求解,如x2=9,则x=±3.
老師:用这种方法能否解更一般的方程呢?如x2=p.
学生:可以,但要分p>0,p=0,p<0三种情况讨论.
老师:“配方法”又是怎么得到呢?
学生:用“直接开平方法”可以解方程(x+1)2=3,将此方程展开、整理后就得到方程x2+2x-2=0,因此可以逆向思考,设法将方程x2+2x-2=0转化为(x+1)2=3的形式,并求解,这就是“配方法”.
老师:“公式法”又是怎样得到的?
老师:“配方法”和“公式法”有什么联系?
学生:“配方法”是“公式法”的基础,“公式法”其实就是省略了配方的过程.
老师:解一元二次方程和解二元一次方程组、解分式方程一样,本质上都是将不会解的“新方程”转化为会解的“旧方程”,这里采用的方法是“降次”.各种不同解法之间是有密切联系的,其中“直接开平方法”是基础,配方法、公式法等是在它的基础上变式应用.
本片断,教师引导回顾不同方程(组)的解法,揭示解方程的基本策略是“化归”,即将不会解的“新方程”转化为会解的“旧方程”.通过对“直接开平方法”、“配方法”、“公式法”推导过程的回顾,揭示各种解法之间的内在联系,帮助学生建立合理的逻辑过程,避免不同解法之间的割裂,在认知上整体把握知识结构.通过回顾,再次感受特殊到一般、具体到抽象、分类讨论等思想方法在解一元二次方程中的作用,而这些知识和方法与后续学习“根的判别式”、“二次函数图象与x轴交点问题”等有密切联系,为后期知识框架的重新构建做了良好的铺垫.
2 抓住数学学习的基本套路,类比学习新的知识系统
在数学中,每一个研究对象都是一个系统,系统内部往往有某种稳定的结构,抓住这种结构进行类比学习,可以简化新系统的学习过程,有效提高学习效率.在学习沪科版九年级下册《圆的基本性质》第一课时,按如下方式复习引入:
老师:从本章开始,我们学习圆的有关知识,学习什么?怎么学习?我们可以回顾三角形的学习历程.
学生:三角形的定义——三角形的表示——三角形的相关要素及其关系(两边之和大于第三边;三个内角之和等于180°)——确定三角形的条件(三角形全等的判定方法)——三角形的性质(等腰三角形的对称性、直角三角形及勾股定理)——两个三角形之间的关系(三角形相似)——三角形与四边形的关系……
学生:研究三角形的常用方法有:观察、操作、分析、比较、推理等.
老师:圆的有关知识的学习也可以按照这样的内容和方法进行.
学生在前面的几何学习中已经积累了三角形和四边形的数学知识研究套路.圆作为初中几何研究的基本对象,虽然它和三角形、四边形是不同的图形,但它的研究内容和方法与三角形、四边形有许多相似之处.对于这种新图形的学习,借鉴已有的知识和经验是非常必要的,回顾三角形相关内容的研究历程和方法,可以想象圆的研究内容和基本方法.通过回顾三角形的知识系统,想象圆的知识系统,可以有效引导学生用系统思维方法发现问题、提出问题、分析问题和解决问题.可以使学生在掌握圆的相关知识的同时,发展“四能”及系统思维能力,有效积累方法迁移的数学活动经验.
同时,圆的学习内容和研究方法也要纳入到学生已有的知识体系中,通过横向和纵向地联系和类比,将三角形、四边形与圆建立新的联系,形成更加完整的知识体系.
3 提炼数学研究的基本方法,提高发现和提出问题的能力
我们对世界的认识,对数学知识的学习往往有一定的规律和方法.通过某一知识的学习,使学生领会和掌握这种规律和方法比掌握知识本身更重要.因此,课堂教学中,不仅要关注知识层面,更要对学习的过程和方法给予重视,帮助学生养成“方法论”的意识.在教学沪科版九年级下册《圆的确定》一课时,进行如下小结(PPT依次呈现):
师生结合PPT,共同回顾本节课学习和探究的历程:
(1)由生活情境“一块残片复原”问题引出课题;
(2)把生活情境抽象成数学问题:已知一段弧,如何确定该弧所在的圆;
(3)提出问题:如何确定一个圆;
(4)思考问题:一个点能否确定一个圆;
(5)动手操作得到反例,说明:一个点不能确定一个圆;
(6)增加限制条件,提出问题:两个点能否确定一个圆;
(7)继续操作得到反例,说明:两个点不能确定一个圆;
(8)再增加限制条件,提出问题:三个点能不能确定一个圆;
(9)通过操作得到猜想:不在同一直线上的三点确定一个圆;
(10)进行数学证明,得到结论:不在同一直线上的三点确定一个圆;
(11)应用结论.
本课小结改变了“谈一谈本节课的收获和体会”、“说一说本节课的疑惑”的空洞模式.引导学生回顾课堂学习的一般过程,感悟“发现问题”、“提出问题”、“分析问题”和“解决问题”的基本思路和方法.这样的小结,还可以让学生感受到“条件由少到多,對象由模糊到清晰”的基本规律,以及“一个数学结论,如果不成立,可以举反例;如果成立,则必须进行证明”的基本方法.这种规律和方法是今后进一步学习的基本方法,掌握它们有助于培养学生“发现问题”、“提出问题”、“分析问题”和“解决问题”的能力.
数学知识是普遍联系的,相同或相近的知识都构成一个系统,系统内的研究方法往往是相同的,而不同系统间在方法和思路上也可以互相借鉴和补充.不同的数学对象往往具有各自稳定的研究套路,但解决问题的基本思想和方法却是相通的.因此,在数学教学中,我们要用联系的观点看待问题,既要关注知识的发生、发展过程,又要及时总结研究问题的基本方法和套路,注重数学的整体设计,着力培养学生的整体观念,努力把学生培养成“既见树木,又见森林”合格人才.
参考文献:
[1] 章建跃.注重数学的整体性,提高系统思维水平[J].中学数学教学参考(中旬),2015(3):4-6.
[2] 章建跃,任党华,郭建明.理解数学内容本质,提升思维教学水平[J].中学数学教学参考(中旬),2015(6):14-19.
