时变条件下军用爆炸品公路运输人口风险路径优化模型研究

刘宝新，谢 伟，张婷婷

(1.军事交通学院 联合投送系,天津 300161； 2.军事交通学院 研究生管理大队，天津 300161; 3.94994部队，南京 210019； 4．军事交通学院 训练部，天津 300161)

● 基础科学与技术 Basic Science & Technology

时变条件下军用爆炸品公路运输人口风险路径优化模型研究

刘宝新1，谢 伟2,3，张婷婷4

(1.军事交通学院 联合投送系,天津 300161； 2.军事交通学院 研究生管理大队，天津 300161; 3.94994部队，南京 210019； 4．军事交通学院 训练部，天津 300161)

为降低军用爆炸品的运输风险，通过对运输过程中人口风险以及实际运输网络动态性分析，建立时变条件下军用爆炸品运输的人口风险模型，利用改进的模拟退火算法思想进行Matlab编程，对时变条件下军用爆炸品运输的风险最小路径进行求解。算例验证表明，只需获得运输网络中各个时段对应的事故概率、人口密度和交通流量等数据，就能利用改进的模拟退火算法较好地解决时变条件下的风险最小路径问题。

时变；军用爆炸品；公路运输；人口风险；路径优化；模拟退火算法

军用爆炸品是部队执行作战任务、进行爆破作业等国防工程不可缺少的组成部分，爆炸品从生产加工到配发部队，公路运输是其中的必经环节。在运输过程中，一旦发生爆炸事故，将会对周边人口和环境产生严重损害。根据公路交通状况、周边人口数量等因素及其随时间变化的规律，科学地选择合适的路径和车辆运行时间，对于降低运输事故发生的概率、减少事故的危害后果都有着积极作用。因此，开展基于时变条件下人口风险的军用爆炸品公路运输路径优化研究，具有十分重要的意义。

1 人口风险模型构建

风险是对事故发生概率和影响后果的度量，在人口风险模型中，一般用事故发生概率和暴露人口数量的乘积表示。其中，事故发生的概率具有时变性，各个时段的事故发生概率可通过对历史数据的统计分析获得。Frank等对不同时段发生的交通事故概率pij(t)统计数据见文献[1]。

对于暴露人口，由于路上人口、路下人口受到的影响程度不同，一般需要对不同区域类型的人口进行区分。由于路上人口相对集中且都沿着道路通行，可将路上人口视为按线性分布。路上人口的线密度可表示为

(1)

式中：AADTij为路段ij上的年平均日交通流量，一般可通过历史统计数据获得；θ为平均每辆车载有的人员数量；vij为路段ij上的平均运行速度；uij为路段ij上的车外人员密度，需要根据道路等级以及当地人口出行特点进行确定。此外，考虑到一级公路、高速公路会对进出口进行限制，可将此类道路的车外人口密度定为0人/km。相对路上人口，路下人口分布相对分散，因此常利用矩形模型或圆形模型对路下人口数量进行评估。由于矩形影响区域模型的误差比半圆形模型更小，故采用矩形模型计算[2]。路下人口密度可根据该地区人口数量以及区域面积求得，并通过各时段人口出行比例系数进行调整得到各个时段的人口密度。其中人口出行比例系数见文献[3]。

若考虑车辆以及建筑物的缓冲作用，还可将人口分为室内人口和室外人口。由此，可将路上人口和路下人口分别表示为

(2)

(3)

式中：xL为车(室)外人口数量的比例，已有学者根据典型路段的人流量和车流量进行统计，可按城市主干道50%，次干道、农村道路30%，高速公路0进行赋值[4]；SFL为车(室)内人员的风险减缓系数，可取为20%[5]；lij为路段长度，km；d为爆炸品的影响半径，km。

由式(1)—式(3)，得各时段暴露人口数量为

(4)

式中：δon和δoff分别为路上人口与路下人口的权重调节系数，由于一旦发生运输事故引发爆炸，路上人口受到的影响要比路下人口大，因此应适当增加路上人口的权重系数比例，参考以往的研究数据，一般可将路上、路下人口的权重系数分别取为0.6和0.4[4]。

根据不同时段人口出行特点以及交通流量的变化，将各路段的事故概率pij(t)、人口数量等按时间段进行划分，可建立基于时变条件下的风险最小路径运输优化模型：

(5)

(6)

(7)

式(5)为针对路径的人口风险最小的目标约束；式(6)为路径是否包括节点i与节点j之间的路段；式(7)为流向约束，表示路径从起点至终点。

2 算法及编程实现

对基于静态网络的路径优化问题已有Dijkstra、Floyd、A*等较为成熟的算法，但对于时变下的路径优化问题，静态网络的算法已不再适用。随着各种智能算法越来越广泛地应用于求解各类问题，遗传算法、蚁群算法、模拟退火算法等智能算法也被用于求解路径优化问题。其中模拟退火算法在全局搜索中有较明显的优势[6]，通过控制降温的速度模拟退火过程搜索最优解。利用Metropolis抽样方法，可使算法以一定的突跳概率产生、接受新解。目前针对模拟退火算法有较多改进，如在产生新解时利用遗传算法的思想对解空间内的个体进行交叉、选择等操作，在产生新解的过程中同时淘汰劣解等。一般模拟退火算法包括初始温度设定、恒温、降温等过程，具体实现步骤如下。

2.1 染色体编码

为使算法能够识别，借鉴遗传算法的思想将解空间的数据用染色体基因的形式表示出来，即染色体编码。目前常用的编码方式有0-1编码、实数编码、格雷码编码[7]等，其中0-1编码具有编码规则简单、易于解码以及便于算法的实现等优点，一般在路网结构不太复杂的情况下使用。0-1编码的规则为：按节点号的顺序依次排列，对应位置的数值为1表示该节点被选中，否则为未被选中。如图1所示的编码，代表路径1—3—5—6—9。

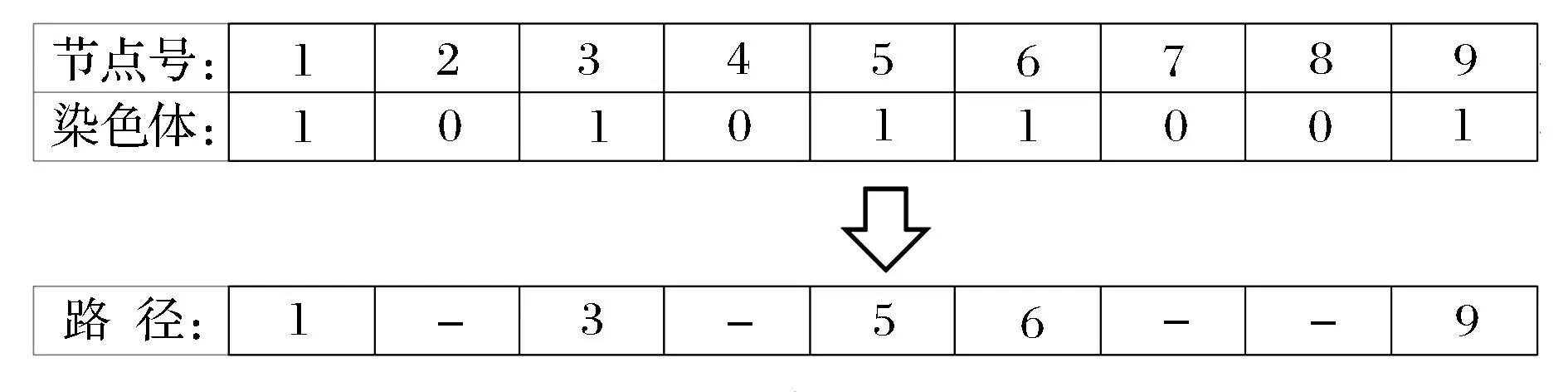
图1 0-1编码和解码

2.2 初始化种群及参数

根据问题的规模，设定初始温度T0、链长L和冷却温度Tend，并利用rand函数随机生成一定规模的初始种群作为路径优化问题的初始解。

v=round(rand(n1,s1));%n1为种群数量，s1为节点数量

v(:,1)=1;

v(:,end)=1;

由于节点1和最后一个节点为必经节点，设定首尾节点被选中。此外，可根据路网结构，排除初始解中不存在的路线。

2.3 恒温操作

在温度T下，利用初始解S1产生新解S2。产生新解的方法为：随机产生两个位置，对相应位置的编码进行交换。如图2所示，随机产生的两个位置为第2位和第6位，将初始解S1的第2位和第6位上的编码进行互换得到新解S2。

图2 产生新解

根据以上算法思想，可利用round函数和rand函数产生两个随机位置，同时为降低产生非法路径(不存在的路径)的概率，可将随机位置限定为首尾节点之间的点，即首尾节点不参与编码交换。实现代码为

function S2=NewAnswer(S1)%产生新解

[m,n]=size(S1);%计算初始解的个数及节点数量

for i=1:m

S2(i,:)=S1(i,:);

a=round(rand(1,2)*(n-3)+2);%产生两个首尾节点之外的随机位置

temp=S2(i,a(1));

S2(i,a(1))=S2(i,a(2));%产生新解

S2(i,a(2))=temp;

end

产生新解S2之后，可利用式(6)计算S2相对于S1的增量df。其中f函数为目标函数，对于本问题为路径的风险值函数。

df=f(S2)-f(S1)

(6)

由于时变特性化，因此f函数应按各时间段的不同风险值来计算路径的总风险。若把时间分为8个时间段，结合式(1)的目标函数，可将f函数用以下代码实现：

function[risk,T]=path_risk (v,D,time,t)%求解路径v的风险函数

% v： 路径代码

% D： 各路段在不同时间段的风险值

% time： 各节点之间运输所需要的时间

% t： 出发时刻

[vm vn]=size(v);%得到v的行数vm，列数vn

T=ones(vm,1)*t; %到达的时刻

risk=zeros(vm,1);%初始化路径的风险值

for i=1:vm

I=find(v(i,:)= =1);%解码

[Im,In]=size(I);%得到I的列数In

for j=1:In-1

t_time=rem(T(i),24);

if t_time= =0

risk(i)=risk(i)+D{I(j),I(j+1)}(1,1);

T(i)=T(i)+time(I(j),I(j+1));

else

k=ceil(t_time/3);

if k= =T(i)/3

k=k+1;

end

risk(i)=risk(i)+D{I(j),I(j+1)}(1,k);

T(i)=T(i)+time(I(j),I(j+1));%加上本段路耗费的时间

end

end

end

根据Metropolis准则并结合增量df的结果来决定是否接受新解，对于求解最小值问题，当df<0时，表示新解S2优于初始解S1，则用新解S2替代初始解S1；当df>0时，则以接受概率e-df/T接受新解S2。

2.4 降温操作

以速率q进行降温，即T′=q×T。在新的温度T′下，重复恒温操作。当温度达到冷却温度Tend时，算法结束，输出最优解。需要注意的是，速率q的取值对算法有较大影响。若取值过小，需要耗费较长时间进行计算，使算法效率降低；若取值过大，则温度下降过快，易错过最优解，使算法陷入局部最优。因此，q的取值需要根据问题的实际情况进行调试选择，其取值范围一般在0.5～0.99之间[8]。

3 算例分析

某部队有一批军用爆炸品需从节点1处运往节点8，假设根据式(1)至(5)及人口密度、人口出

行系数等参数计算出8个时间段的人口风险见表1。为简化问题，各路段的运输时间设为固定值，运输网络如图3所示，图中标注的路权值为各路段所耗费的运输小时数。据此求解运输风险的最小路径以及相应的出发时刻，确定该部队运输军用爆炸品的合理路线以及相应出发时间。

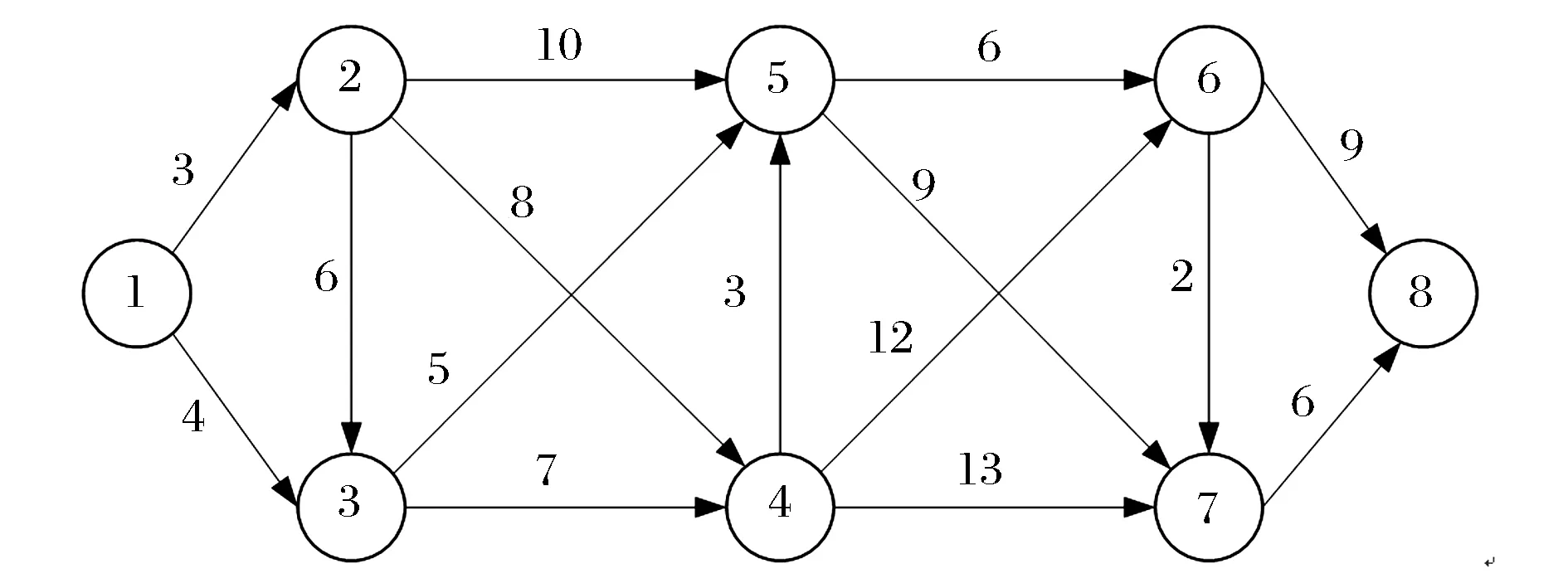
图3 运输网络

根据上文所述思想和方法利用Matlab进行编程，由于目前针对算法参数赋值的理论都只能给出取值范围，因此参数的具体设定还需要通过不断的调试来确定。通过调试，将初始温度设为1 000，冷却温度设定为0.001，降温速率设定为0.9，链长设定为50。以6:00—18:00作为出发时刻的选择区间，每隔10 min计算一次风险最小的路径，计算结果见表2，其中出发时刻“6:10—6:50”表示当出发时刻为6:10、6:20、6:30、6:40、6:50时其风险最小路径相同。

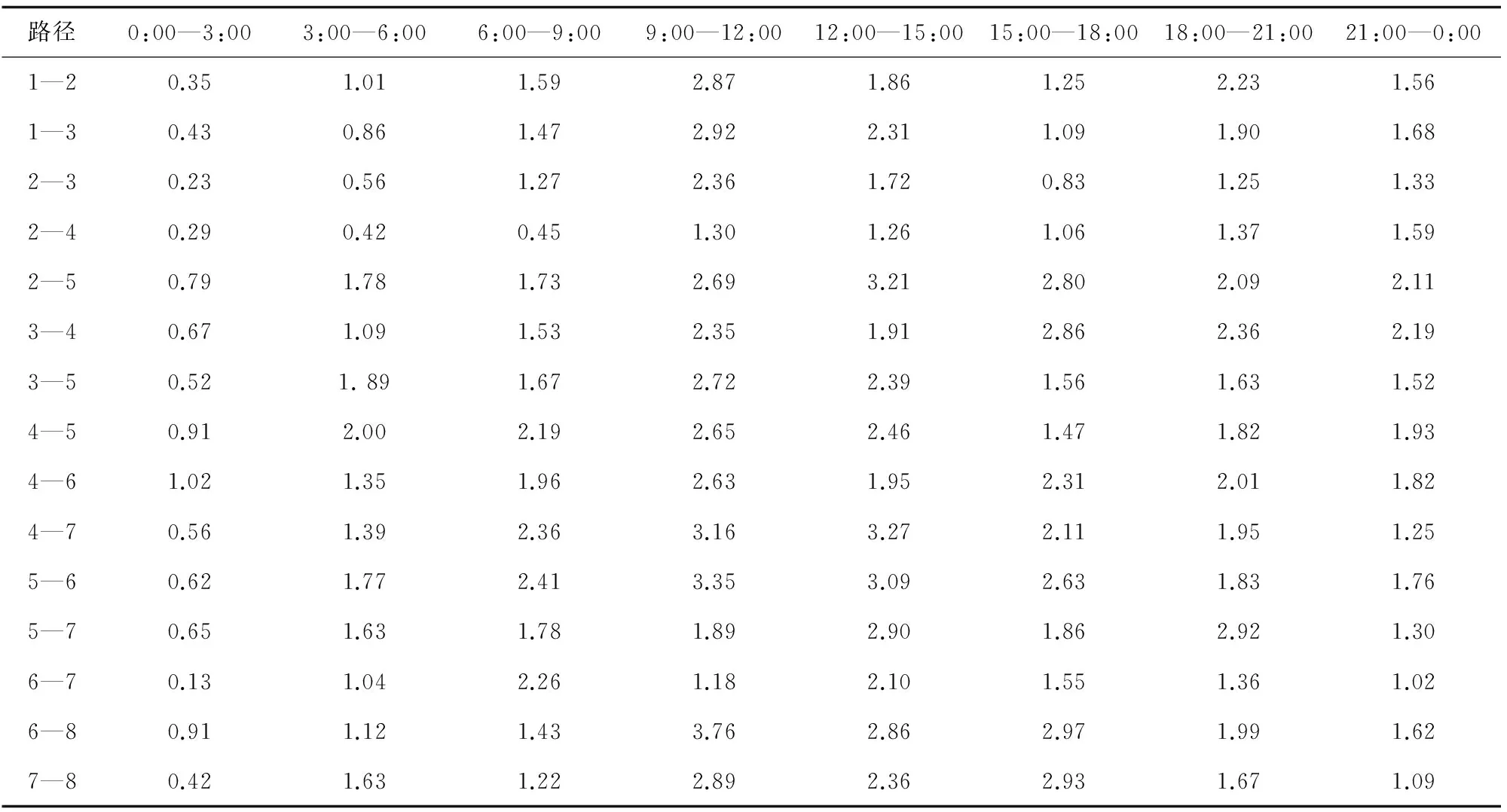
表1 各运输时段的人口风险

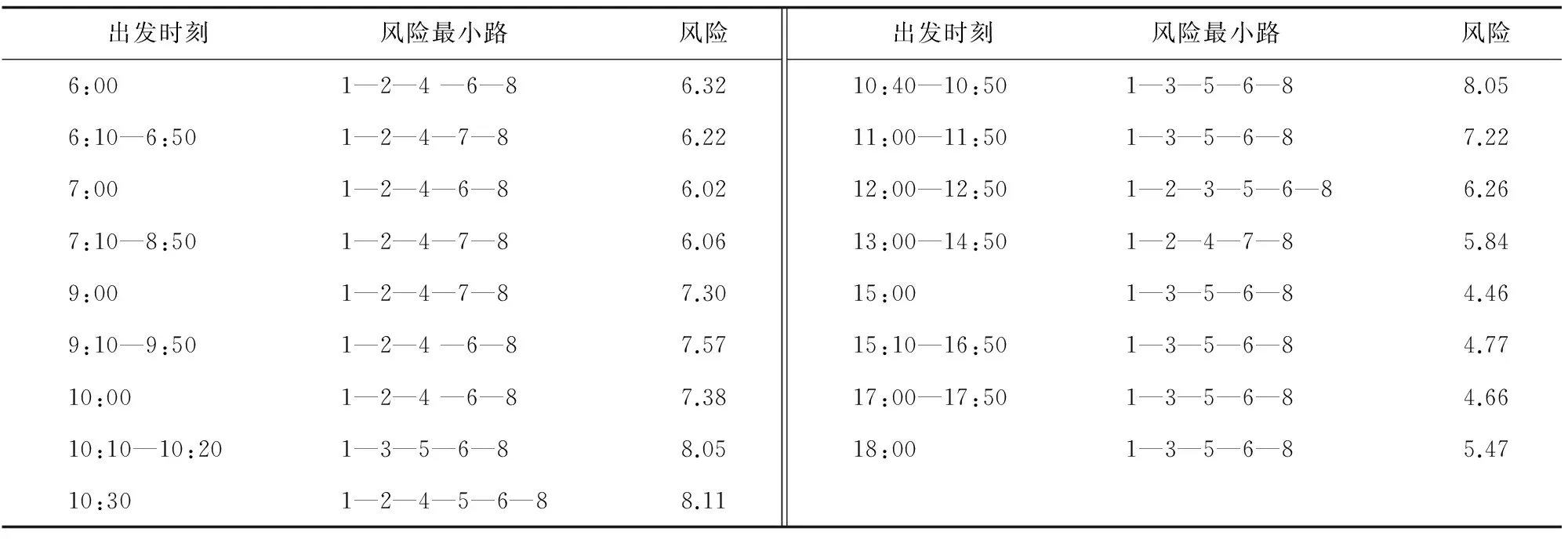
表2 计算结果

根据表2的计算结果可知，该部队运输军用爆炸品风险最小的路径为1—3—5—6—8，运输总风险为4.46，对应于15:00从节点1出发。不同的出发时刻会导致运输的风险不同，最小风险路径也会发生相应的变化。如6:00和6:10出发时运输风险最小的路径在第3个节点发生了变化，风险值相差0.1。在15:00出发时，路径1—3—5—6—8的运输风险最小，需耗时24 h，而根据图3可求得时间最短路径1—3—5—6—7—8，需耗时23 h。可见，风险最小的路径与时间最短路径并不一定是同一条路径，同样即使对于同一条路径，其风险值也有可能会随出发时间的不同而发生变化，如对于路径1—2—4—6—8，6:00出发和7:00出发的风险值相差0.3。

4 结 语

由于运输网络随时间动态变化，单一的静态网络并不能客观地反映运输风险的变化情况。为更加准确、客观地评估运输风险从而得出风险较小的路径，使部队遂行军用爆炸品运输任务更加安全、可靠，应当从时变角度对路网的风险进行评估。通过算例验证说明，只需获得运输网络中各个时段对应的事故概率、人口密度和交通流量等数据，就能利用改进的模拟退火算法较好地解决时变条件下的风险最小路路径问题，与基于静态网络的评估方法相比更加贴近运输的实际情况。同时，算法在设计时采用细胞数组储存路段参数，对新样本数据的适应能力较强，可根据任务性质和侧重点的不同，通过运输时间、费用等指标评估相应的最短时路径、运费最小路径等，可为部队执行军用爆炸品运输时，在路径选择方面提供一定程度的决策支持和参考。

[1] FRANK W C，THILL JC，BATTA R．Spatial decision support system for hazardous material truck routing[J]．Transportation Research Part C Emerging Technologies，2000,8(1-6)：337-359．

[2] 赵天一．基于风险分析的危险品车辆路径优化问题研究[D]．天津：天津大学，2013．

[3] 西安市城乡建设委员会，长安大学．西安市城市交通可持续发展研究[EB/OL](2005-12-16)[2016-05-06]．http:// www.docin.com/touch-new/preview-new.do?id=504089821．

[4] 沈小燕．道路危险货物运输风险分析及路线优化研究[D]．西安：长安大学，2009.

[5] 任常兴．基于风险分析的危险品道路运输路径优化方法研究[D]．天津：南开大学，2007．

[6] 王勇为，李昱.模拟退火算法在军事运输路径优化中的应用及求解[J].国防交通工程与技术，2009，7(4)：23.

[7] 李清，胡志华．基于多目标遗传算法的灾后可靠路径选择[J]．浙江大学学报(工学版)，2016，50(1)：33-40．

[8] 梁旭，黄明，宁涛，等．现代智能优化混合算法及其应用[M]．北京：电子工业出版社，2014：117．

(编辑：史海英)

Population Risk and Route Optimization Model of Military Explosives Highway Transportation in Time-varying Condition

LIU Baoxin1, XIE Wei2,3， ZHANG Tingting4

(1.Joint Projection Department, Military Transportation University, Tianjin 300161, China;2.Postgraduate Training Brigade, Military Transportation University, Tianjin 300161, China;3.Unit 94994, Nanjing 210019, China； 4．Training Division, Military Transportation University, Tianjin 300161, China)

To reduce the risk of military explosives transportation, the paper firstly establishes population risk model of military explosives transportation in time-varying condition by analyzing population risk during the transportation and the network dynamic of actual transportation. Then, it programs with improved simulated annealing algorithm and Matlab, and solves the minimum risk path of military explosives transportation in time-varying condition. The result shows that obtaining the data of accident probability, population density, and traffic flow can solve the problem of minimum risk path with improved simulated annealing algorithm in time-varying condition.

time-varying; military explosives; highway transportation; population risk; route optimization; simulated annealing algorithm

2016-10-10；

2017-02-18． 作者简介： 刘宝新(1966—)，男，博士，教授，硕士研究生导师．

10．16807/j.cnki.12-1372/e.2017.07.019

U116．2

A

1674-2192(2017)07- 0081- 05