不同攻击策略下快递配送网络抗毁性分析
2017-08-26付秀琴李腾
付秀琴+李腾


摘 要:针对快递配送网络的特征,基于复杂网络理论与图论建立快递配送网络结构模型,设计网络抗毁性测度模型,定量研究在不同攻击策略下攻击网络节点与路径时快递配送网络的抗毁性能的特征。研究表明网络连通率能很好地反映快递配送网络的抗毁性能,且网络抗毁性是由少数节点和边维系的;边的抗毁性高于节点的抗毁性,蓄意攻击对网络抗毁性的影响程度比随机攻击的大,快递配送网络更符合无标度网络特性。
关键词:快递网络 抗毁性 计算机仿真 攻击策略
中图分类号:F252
文献标识码:A
文章编号:1004-4914(2017)06-075-04
一、引言
最近几年,我国电子商务发展迅速,交易额连创新高,特别是B2C模式下的网络零售业更是增长迅速。在近几年我国GDP中高速增长的背景下,电子商务零售业以其2-3倍的速率快速发展,成为拉动国民经济的重要动力。然而在电子商务发展迅速的同时,我国的物流发配送水平却没有跟上电商企业的脚步,特别是快递配送效率严重制约着电子商务的快速发展。据统计,仅2015年“双十一”一天,天猫的日交易额就达912.17亿元,7年间增长了1800倍,“双十一”期间处理快件数量达7.8亿件。全国主要电商物流均发生网点爆仓现象,导致物流速度慢,无法保证送达时间,客户投诉现象频发,类似“双十一”这种特殊节日对配送网络的冲击性和破坏性越发严重。这种特殊情况下,电商物流量的急剧增加对配送网络的要求越来越高。过去,大多数研究集中在降低快递的配送成本和提高配送效率,但是近年来,特殊节假日如“双十一”对快递配送网络的沖击越来越大,快递网络优化设计在传统考虑成本与效率的同时,应更加关注网络的稳定性与抗毁性。近年来对快递配送网络的研究越来越受到重视,成为快递配送网络优化新的突破点。
最初,对网络抗毁性的研究多基于图论,应用范围较小。几年来,随着复杂网络理论在各个学科的应用越来越成熟,应用复杂网络理论研究管理、经济等领域的问题逐渐成为新的研究热点。由于现实世界的网络系统往往是大规模的复杂系统,设计个体多,且个体特性不同,同时个体之间存在复杂的联系,传统的理论无法解决这些问题,而复杂系统理论恰好重视研究个体之间的关系以及系统的整体状况。因此,复杂系统理论在网络抗毁性领域的研究应用越来越多,成为当前研究网络抗毁性的主要理论之一。快递配送网络包含多个节点与配送线路,节点之间存在货物与信息的交互,是典型的复杂网络。目前,学者们对快递物流网络抗毁性的研究已做了初步尝试如:黄仁全等(2012)采用自然连通度作为网络抗毁性的测量指标,研究作战网络在面临不同的攻击策略时的抗毁性的变化特征;王敏功等(2012)应用复杂网络理论与方法,分析应急物流网络在面临不同形式的攻击时的抗毁性特征;刘庆法等(2014)首先采用采用原始与对偶相结合的方法构建了区域高速公路网络的拓扑结构,应用复杂网络理论的各项统计指标平均路径长度、聚集系数、网络效率等对高速公路网络的抗毁性进行了定量分析,考察在不同攻击方式下,网络的抗毁性特征;郑文强等(2015)针对航材配送网络节点多,配送路线错综复杂等特点,设计了网络全局效率与加权抗毁度作为网络抗毁性的测度指标,对航材配送网络的抗毁性进行了定量研究。
目前学者们应用复杂网络理论研究快递配送的相关成果还较少,主要集中于论述快递配送网络符合小世界网络与无标度网络的特征,缺乏系统性的深入的研究。本文针对快递配送网络的特征,基于复杂网络理论与图论建立快递配送网络结构模型,设计快递配送网络抗毁性测度模型,修正了节点介数的攻击策略,结合matlab对网络抗毁性进行仿真分析,研究在不同攻击策略下攻击网络节点与路径时快递配送网络的抗毁性能的特征,为快递配送网络的构建与优化提供依据。
二、快递配送网络模型
(一)问题描述
目前的快递配送网络主要分为两种:轴辐式网络和全连通式网络。应用较多的是轴辐式网络,轴辐式网络是指在货物运输过程中,货物不再是从供应地直接配送到需求地,而是经过中间节点(一般是区域型枢纽站或转运中心)进行分类后分批配送,这种配送网络可以实现规模效用,节约成本。对于快递配送网络而言,其枢纽站常常是区域的快件转运中心、仓库等,负责快件的分类、存储、分拨与调配,其末端配送节点通常以加盟的方式参与,从其所在区域的转运中心分取快件,以门店的方式直接面对收件人,进行直接配送。本文基于轴辐式快递配送网络进行研究。
在快递配送网络中,节点主要有两类,一是区域转运中心,二是末端配送节点。这些节点以及它们之间的配送线路构成整个网络结构并伴有快件与信息的流动共同构成了快递的配送网路系统。为了更好地对快递配送网络的抗毁性进行研究,本文不讨论快递配送网络模型建如何立,而是重点研究快递配送网络的抗毁性能,在建立快递配送网络结构模型之前,作如下假设:不考虑配送线路的方向,整个配送网络为无向图;假设基于最小成本与最高效率等目标约束的配送网络模型已建立;每条配送线路的快件流量都不超过该路径所能承受的最大货物流量,各节点承担的快件量均在其可承受范围内;每个末端配送节点只能从其所在区域的配送中心接受快件,进行快件与信息的交互。
(二)网络模型
根据问题描述,快递配送网络涉及到快件的接受、分发、转运、储存运输等多种因素和节点,为保障快件配送的及时性与高效性,本文将各转运枢纽中心和各末端派送点作为网络节点,节点之间配送路径作为网络中的边。对于快递配送网络而言,快递的量和配送距离直接影响快递配送的效率,各节点的重要程度也引起流量不同而不同,明显地,配送转运中心的流量大,其在整个配送网络中的地位也相对重要。因此,在描述快递配送网络时,节点的流量与路线的距离必须考虑。
用G(V,E,S,U)表示快递物流配送网络,V表示配送网络中的大型转运枢纽中心和各末端配送节点的集合,若记V=n表示快递配送网络中存在n个节点,V=(v1,v2,…,vn);E表示网络边的集合,若记E=m,表示网络中存在m条边,E=(e1,e2,…,em);S表示各条边的长度(距离)的集合s│i,j∈n,U表示两点之间流量的集合,ui,j│i,j∈n构成的快递配送网络结构如图1所示。
三、快递配送网络抗毁性测度模型
网络的抗毁性通常是指当网络中的部分节点或边被破坏(包括随机破坏与蓄意破坏)时,网络能恢复其主要功能的能力。快递配送网络遭受攻击后,配送点和配送线路就会失效,影响其所在区域的快件配送效率,严重的甚至影响真个网络的连通,造成重大的损失。对于快递配送网络而言,当其遭到攻击后,人们最关心的便是其对整个快递网络连通效率的影响。
当前,在复杂网络理论对网络抗毁性测度的研究领域,不同的学者提出了不同的测度指标。提出了诸如基于平均最短路径、极大连通子图,网络最大连通度以及加权抗毁度等测度指标建立的网络抗毁性测量模型来研究网络的抗毁性的特征。由于快递配送网络具有自身的特殊性和复杂性,网络各节点之间的互动和协同,使快递配送网络呈现复杂的网络结构,如何定性和定量认识和度量快递配送网络遭受不同攻击方式的破坏后网络的抗毁性能,将对快递配送网络的规划与管理起到非常重要的作用。
平均最短路径常常作为度量网络抗毁性的重要指标,最短路径是指网络中节点Vi和Vj的最短路径指从Vi出发经过最少的边到达节点Vj的边的条数,网络中任意两个节点的最短路径平均值称为网络的平均最短距离,即网络的平均最短路径距离可表示为:
其中vi,vj,为网络中的两个节点,i,j∈n,d(i,j)表示vi,vj之间的最短距离。
平均最短路径恰好体现了快递配送网络效率最高这一规划目标,通过快递配送网络的平均最短路径随着网络遭受破坏的程度的加大的变动可以测量快递配送网络的抗毁性,平均最短路径的增量越大,說明网络的抗毁性能越差。当快递配送网络遭受突然破坏后,网络中的节点和路径可能失去其功能而被删除,若是区域的配送中心受到攻击,其下属的末端配送节点也失去存在的意义,成为孤立的节点,这些孤立节点的最短路径将为零,这将导致网络整体的平均最短路径失去单调性,会先变大后变小,这种现象将对网络抗毁性的测量造成影响。因此,将网络中两个节点vi与vj之间的连通率定义为节点vi与vj之间最短距离d(i,j)的倒数,所有节点对之间的连通率平均值定义为网络连通率,记为E(G),即可利用网络连通率来测量网络的抗毁性,网络连通率E(G)表示为:
四、快递配送网络攻击策略分析
(一)快递配送网络的攻击方式
从快递配送网络的拓扑结构来看,对网络进行攻击主要有两种攻击方式:攻击节点与攻击边。
快递配送网络的节点遭到攻击主要原因有由于特殊时期如“双十一”,导致配送中心爆仓,或配送中心受不可抗力的影响发生意外事故,或者由于业务量减少导致区域配送中心的关闭,这种攻击常常会产生较大的影响;末端配送节点多以加盟的方式参与到配送网络中,加盟者随机波动性较大,且较长发生,但其对整个快递配送网络结构的影响较小。快递配送网络的节点在网络中的重要程度不同,对于转运枢纽中心而言,一旦其遭到攻击,其所在区域的所有配送路径也同时失去意义,即对于攻击节点而言,节点一旦遭到破坏,与之相邻的边也没有存在的意义,所以本文采取攻击节点时,对节点与其相邻的边进行删除的方式。
快递配送网络边遭到破坏主要由于道路拥堵、城市道路规划改建以及恶劣天气等造成的,在遭受攻击时快递配送企业处于被动地位,对配送网络的畅通性与稳定性在短期内影响较大。对于攻击边而言,当某条配送路径故障时,其相邻的配送路线与节点并不受影响,所以,对攻击边时,采用删除该边进行处理。
(二)快递配送网络的攻击类型
本文研究快递配送网络可能面临的两种攻击:一种是随机攻击,另一种是蓄意攻击。
随机攻击相对简单,对网络中的节点或边随机进行删除,此时,各节点或边被选中删除的概率是相等的,与规模大小,重要程度无关。蓄意攻击是按照各节点或边的重要程度的大小,先对各节点或边进行排序,由大到小依次进行删除。
攻击策略是指采取何种方式或规则删除网络中的节点或边。在现有研究中,对节点重要程度的测量指标主要是节点或边度数和介数,将节点度数或介数以由大到小的顺序依次删除或随机删除。
由快递配送网络模型可知,快递配送网络是一个具备流量关系的运输网络,对于快递配送网络,度并不一定代表顶点的重要程度,因为它没有考虑节点和边的规模和容量,节点度并不能充分说明节点在网络中的的重要程度。在图论中,网络的介数反映了相应的顶点或者边在整个网络中的作用和影响力,同时也能反映网络规模可承担的流量大小,因此,基于介数攻击研究快递配送网络的抗毁性更具有现实性与研究意义。基于上述分析,考虑快递配送网络的特性,本文拟采用基于介数的攻击策略来研究快递配送网络的抗毁性。
在复杂网络理论中,节点或边的介数是指,网络中经过该节点或边的最短路径的数目与网络中所有最短路径数之间的比值,具体表示为:
其中,CB(v)表示网络中各顶点的介数,σww'(v)表示顶点w与w'之间所有最短物流路径中经过v顶点的所有路径的数量,σww'(e)为顶点w与w'之间所有最短物流路径的数量。CB(e)表示网络边介数,σww'(e)表示顶点w与w'之间所有最短物流路径中经过边e的所有路径的数量。
对于快递配送网络而言,网络中的各条配送线路与节点通过的快件的最大物流量存在差异,不仅与规模有关与所在区域的业务量也有关,按传统的节点(或边)介数的计算方法,及时节点或边的流量不同,也可能导致介数计算结果相同难以体现快递配送网络的特征,基于此,考虑攻击网络流量大的边(节点)和流量小的边(节点),给网络带来的危害显然不同,现将本快递配送网络的节点介数定义为:
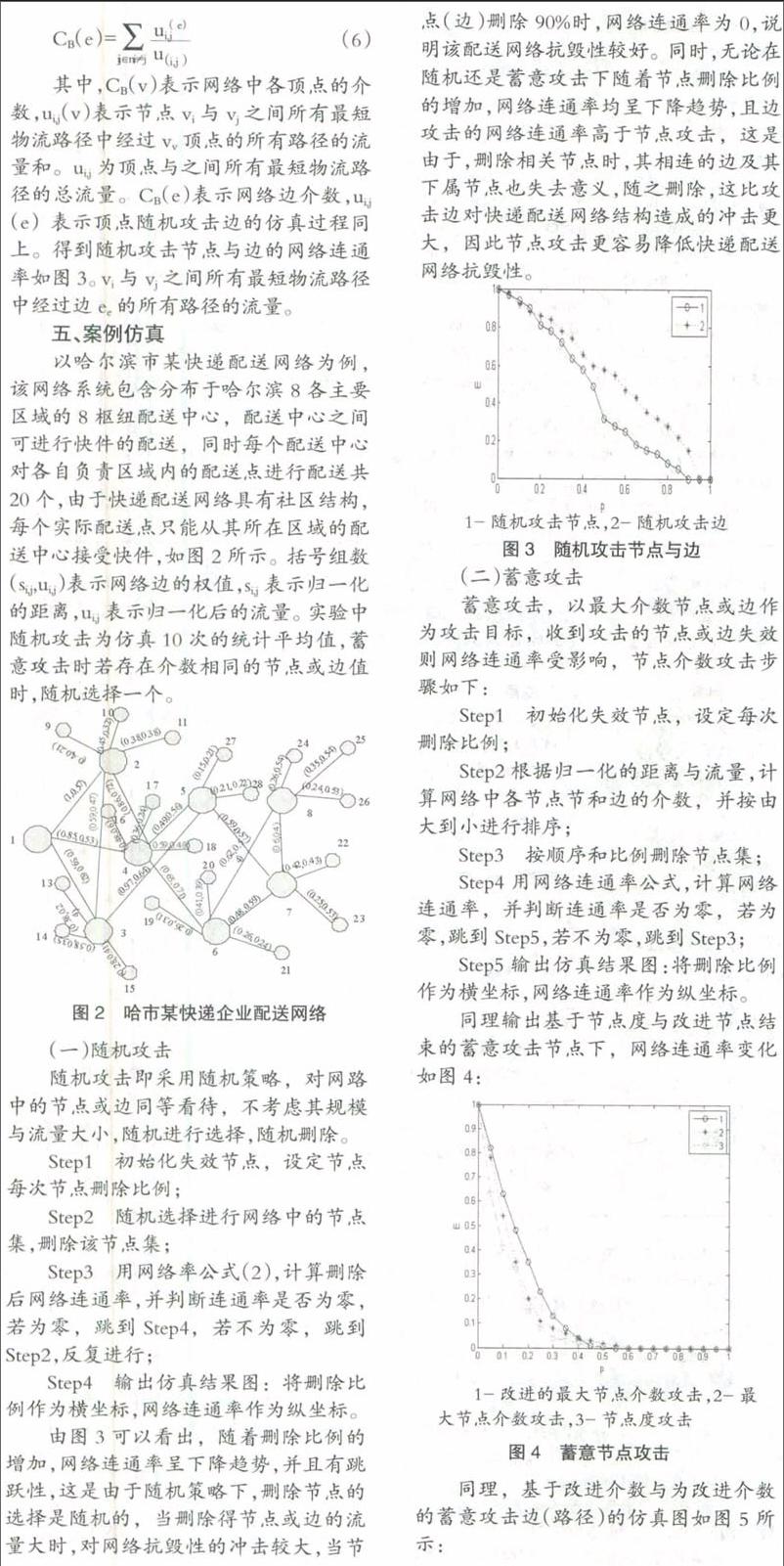
其中,CB(v)表示网络中各顶点的介数,ui,j(v)表示节点vi与vj之间所有最短物流路径中经过vv顶点的所有路径的流量和。ui,j为顶点与之间所有最短物流路径的总流量。CB(e)表示网络边介数,ui,j(e)表示顶点随机攻击边的仿真过程同上。得到随机攻击节点与边的网络连通率如图3。vi与vj之间所有最短物流路径中经过边ee的所有路径的流量。
五、案例仿真
以哈尔滨市某快递配送网络为例,该网络系统包含分布于哈尔滨8各主要区域的8枢纽配送中心,配送中心之间可进行快件的配送,同时每个配送中心对各自负责区域内的配送点进行配送共20个,由于快递配送网络具有社区结构,每个实际配送点只能从其所在区域的配送中心接受快件,如图2所示。括号组数(si,j,ui,j)表示网络边的权值,si,j表示归一化的距离,ui,j表示归一化后的流量。实验中随机攻击为仿真10次的统计平均值,蓄意攻击时若存在介数相同的节点或边值时,随机选择一个。
(一)随机攻击
随机攻击即采用随机策略,对网路中的节点或边同等看待,不考虑其规模与流量大小,随机进行选择,随机删除。
Step1 初始化失效节点,设定节点每次节点删除比例;
Step2 随机选择进行网络中的节点集,删除该节点集;
Step3 用网络率公式(2),计算删除后网络连通率,并判断连通率是否为零,若为零,跳到Step4,若不为零,跳到Step2,反复进行;
Step4 输出仿真结果图:将删除比例作为横坐标,网络连通率作为纵坐标。
由图3可以看出,随着删除比例的增加,网络连通率呈下降趋势,并且有跳跃性,这是由于随机策略下,删除节点的选择是随机的,当删除得节点或边的流量大时,对网络抗毁性的冲击较大,当节点(边)删除90%时,网络连通率为0,说明该配送网络抗毁性较好。同时,无论在随机还是蓄意攻击下随着节点删除比例的增加,网络连通率均呈下降趋势,且边攻击的网络连通率高于节点攻击,这是由于,删除相关节点时,其相连的边及其下属节点也失去意义,随之删除,这比攻击边对快递配送网络结构造成的冲击更大,因此节点攻击更容易降低快递配送网络抗毁性。
(二)蓄意攻击
蓄意攻击,以最大介数节点或边作为攻击目标,收到攻击的节点或边失效则网络连通率受影响,节点介数攻击步骤如下:
Step1 初始化失效节点,设定每次删除比例;
Step2根据归一化的距离与流量,计算网络中各节点节和边的介数,并按由大到小进行排序;
Step3 按顺序和比例删除节点集;
Step4用网络连通率公式,计算网络连通率,并判断连通率是否为零,若为零,跳到Step5,若不为零,跳到Step3;
Step5输出仿真结果图:将删除比例作为横坐标,网络连通率作为纵坐标。
同理输出基于节点度与改进节点结束的蓄意攻击节点下,网络连通率变化如图4:
同理,基于改进介数与为改进介数的蓄意攻击边(路径)的仿真图如图5所示:
由图4可以看出,对于整个网络抗毁性而言,基于节点度与原有的介数改进后的介数攻击网络抗毁性变化不同,这说明改进介数攻击的必要性,更符合快递配送网络的实际运行情况。基于改进介数的蓄意攻击的快递配送网络的连通率基本上均高于基于节点度与和未改进节点介数的网络连通率,这是由于基于改进介数的情况下的蓄意攻击不仅考虑了节点与边的在整个快递配送网络中的重要程度,同时考虑了节点的流量。对于同样级别的节点如果其流量不同,边的长度即运输距离不同,在网络中的重要程度是不同的。
由图4和图5均可以看出,无论是进行节点攻击还是边攻击,在蓄意攻击策略下,网络抗毁性在初期下降较快,抗毁性对网络破坏程度的反映更加明显,当下降到某一值是,下降趋势趋于平缓,这是由于蓄意攻击时,总是先选择网络中节点或边介数较大即更加重要的节点作为删除对象,这些节点或边对整个网络的连通性的作用较大,一旦受到攻击,会引起整个网络剧烈的变动,导致其下属节点成为孤立点。这符合轴辐式快递配送网络的特征。
六、结论
本文从快递配送网络轴辐式特征出发,应用复杂网络相关理论与方法,建立快递配送网络结构模型与网络抗毁性测度模型,详细分析快递配送网络的抗毁性能,并基于快递配送网络的特点对攻击介数模型进行了修正,最后通过计算机仿真,从理论分析和仿真实验结果证明网络连通率能很好地反映快递配送网络的抗毁性能;无论是节点攻击还是边攻击,蓄意攻击对网络抗毁性的影响程度比随机攻击的大,即快递配送网络更符合无标度网络特性,具体表现为对随机攻击的抗毁性和蓄意攻击的脆弱性。相同失效比例和攻击策略下,边的抗毁性比节点的高;快递配送网络的抗毁性能是由少数节点和边维系的,因此,识别并避免这些关键节点和边失效尤为重要。在进行快递配送网络规划时,可依据蓄意或随机攻击概率的大小进行设计。
参考文献:
[1] Weltevreden J.W.J.,Rotem-Mindali O. Mobility effects of b2c and c2c ecommerce in the Netherlands:a quantitative assessment[J].Journal of Transport Geography,2009(2)
[2] 尤寶庆.基于电子商务下的城市配送体系的构建[J].物流工程与管理,2015(4)
[3] Journeau P.,Mercier A.. Design and implementation of a last mile parcel delivery network[C].Strasbourg:European Transport Conference,2011
[4] Cohen R, Raml jak D, ?elmi? M, et al. Bee colony optimization for the pcenter problem[J]. Computers & Operations Research,2011(10)
[5] Paul G, Tanizawa T, Havlin S, Stanley HE. Optimization of Robustness of Complex Networks[J].The European Physical JournalB,2004(38)
[6] Yukio Hayashi, Jun Matsukubo. Improvement of the robustness on geographical network by adding shortcuts[J].PhysicaA,2007
[7] 黄仁全,李为民.不同攻击策略下作战体系网络抗毁性研究[J]. 复杂系统与复杂性科学,2012(3)
[8] 王敏功,王伟,蒋泓松等.基于复杂网络理论的应急物流网络可靠性仿真研究[J].物流技术,2012(19)
[9] 刘庆法,陈红,周继彪等.基于复杂网络理论的高速公路网抗毁性研究[J].公路,2014(6)
[10] 郑文强,陈云翔,庄骏等.基于复杂网络理论的航材配送网络抗毁性分析[J].火力与指挥控制,2015(2)
[11] 倪玲霖,史峰.多分配快递轴辐网络的枢纽选址与分配优化方法[J].系统工程理论与实践,2012(2)
[12] 吴俊,谭跃进,邓宏钟等.基于不等概率抽样的不完全信息条件下复杂网络抗毁性模型[J].系统工程理论与实践,2010(7)
[13] 谭跃进,吴俊,邓宏钟.复杂网络抗毁性研究进展[J].上海理工大学学报,2011(6)
[14] 谭跃进,邓宏钟.基于自然连通度的复杂网络抗毁性分析[J]. 复杂系统与复杂性科学,2014(1)
(作者单位:哈尔滨商业大学管理学院 黑龙江哈尔滨 150028)
(作者简介:付秀琴,硕士,研究方向:物流与供应链管理。)
(责编:贾伟)
