对衣物潮湿后变暗现象的光学分析

冯 禹，王 广，赵 敏，李佛生

(同济大学 物理科学与工程学院，上海 200092)

对衣物潮湿后变暗现象的光学分析

冯 禹，王 广，赵 敏，李佛生

(同济大学 物理科学与工程学院，上海 200092)

理论分析了衣服潮湿后变暗的物理机制，从Kubelka-Munk函数出发推导了湿润介质在不同条件下的反射率，并通过积分球测定了衣物的含水量与光反射率的关系. 实验结果表明：介质基底散射与吸收性质的变化是衣物潮湿后变暗的主要原因,衣物的潮湿程度和光反射率呈负相关.

反射率；散射率；吸收率;漫反射；积分球

生活中我们常常看到这种现象，衣物被打湿后颜色明显变暗. 潮湿衣物变暗的物理机制是什么？潮湿的程度与变暗之间又有怎样的关系？该问题一经第28届世界青年物理学家锦标赛提出即受到了众多物理学爱好者的关注[1]. 早在1988年Lekner[2]等人便利用多次反射的模型对潮湿变暗的现象进行了解释，但该模型无法说明潮湿程度与变暗之间的关系，同时缺乏相关的实验支撑. 本文利用积分球测定了反射率和潮湿程度的关系，并从Kubelka-Munk函数出发，理论推导了潮湿衣物光反射率和散射率等参量的定量关系，理论分析与实验结果吻合.

1 潮湿变暗现象理论分析

如图1所示，在显微镜下，可以看到干燥的衣物表面存在杂乱的纤维，浸湿时衣物纤维之间的缝隙被填满，水和介质充分混合.

(a)干燥 (b)湿润图1 衣物显微图像

当自然光入射介质时，介质的表面同时发生镜面反射与漫反射，如图2所示. 一般情况下，2种反射光的强度比例由介质表面的粗糙度决定，镜面反射强度IS和漫反射强度ID之比为[3]

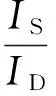
(1)

其中θ为入射角,λ为入射波长，粗糙度Rq定义为介质表面高度的均方差：

(2)

只要求得在一定粗糙度下的镜面反射率和漫反射率，可通过(1)式计算得到两者的比例，从而计算出湿润纤维的实际反射率.

图2 光路示意图

下面首先求光在介质表面的镜面反射率RS，由菲涅尔公式[4]可得：

(3)

其中i1和i2分别为入射角与折射角，且满足折射定律

(4)

考虑湿润介质，此时由于水与介质充分混合，介质的折射率发生变化，将水和介质看作整体，等效介质的折射率为水的折射率和干燥介质折射率的线性叠加：

n21′=msns+mlnl,

(5)

其中ns和nl为干燥介质和液体的折射率，ms和ml为比例系数，两者满足

ms+ml=1.

(6)

当ms=0时，反射介质为纯水；当ml=0时，反射介质为干燥衣物.ms和ml与滴加液体的量有关，实验中获得液体质量所占整体质量的比例，通过(3)～(6)式计算得到介质的镜面反射率.

介质的漫反射率RD由吸收系数K和散射系数S决定，由Kubelka-Munk函数[5]给出

(7)

与镜面反射类似，假设湿润介质的吸收系数和散射系数的比值满足线性叠加关系，即等效吸收系数K′和散射系数S′之比为

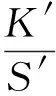
(8)

在实验中介质的吸收系数和散射系数往往不能直接获得,但由(7)式可将两者的比值反解出：

(9)

这样在实验中只要获得2组不同湿度下介质的漫反射率，便可通过(7)～(9)式计算得到任意湿度下的吸收系数和散射系数之比以及对应湿度下的漫反射率. 确定镜面反射率和漫反射率后，可得到给定条件下的湿润介质反射率，其值和介质的粗糙程度、折射率、吸收率、散射率以及入射波长有关，综合(1)～(9)式可以得到湿润介质反射率表达式为

(10)

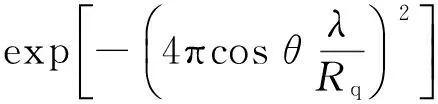
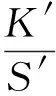
(11)

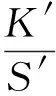
2 潮湿变暗现象实验研究

对衣物被打湿后颜色变暗现象进行了实验研究,实验装置如图3所示. 实验中采用全波段光源，利用光栅分光计来选取特定波长的光，并利用积分球搭建测量装置,对衣物反射率进行了测量. 积分球内涂有反射率>99%的硫酸钡涂层，可使反射光均匀地分布在积分球内表面，这样便可通过测量积分球内一小块面积的反射光强得到整个介质的总反射率. 对于红色纤维，红色波段的光被反射，其余波段光被吸收，因此实验中选取波长范围为650～800 nm的反射光为研究对象.

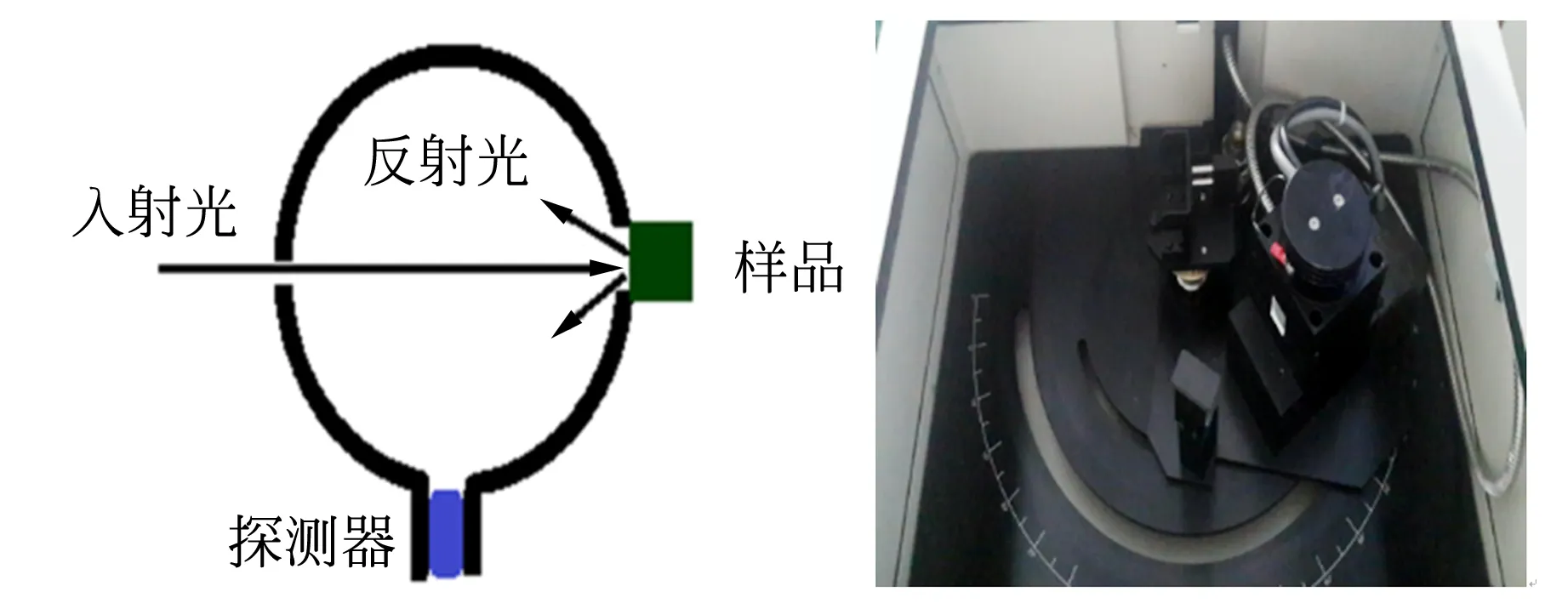
图3 实验装置图

定义纤维潮湿程度η为

(12)

先标定介质在2种不同湿度下的吸收系数和散射系数，从而计算任意湿度下的反射率. 实验中选取完全干燥的纤维和完全饱和的纤维来进行标定，所选取的纤维完全饱和时潮湿程度η=52.7%，在完全干燥时的潮湿程度η=0，标定的吸收系数与散射系数的比值如图4所示.

实验中通过蒸发的方式改变纤维的含水量，分别获得潮湿程度为47.8%，24.1%，12.7%的湿润纤维. 利用上述自搭设备对不同潮湿程度的纤维表面光反射率进行实验测量. 利用图4中标定的K/S和(8),(9),(11)式，理论计算得到3种潮湿程度下的反射率理论曲线.

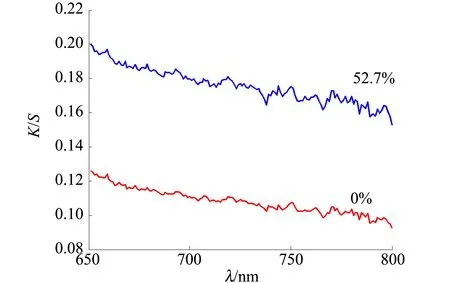
图4 干燥与饱和时介质的K/S值

从图5可以看到理论和实际符合得很好. 纤维的反射率随湿度的增加而减小. 由(8)～(12)式分析，可以得到纤维表面的反射率和潮湿程度的理论关系. 以特定波长700 nm为例，如图6所示，纤维表面的光反射率随纤维潮湿程度的增大而显著下降.

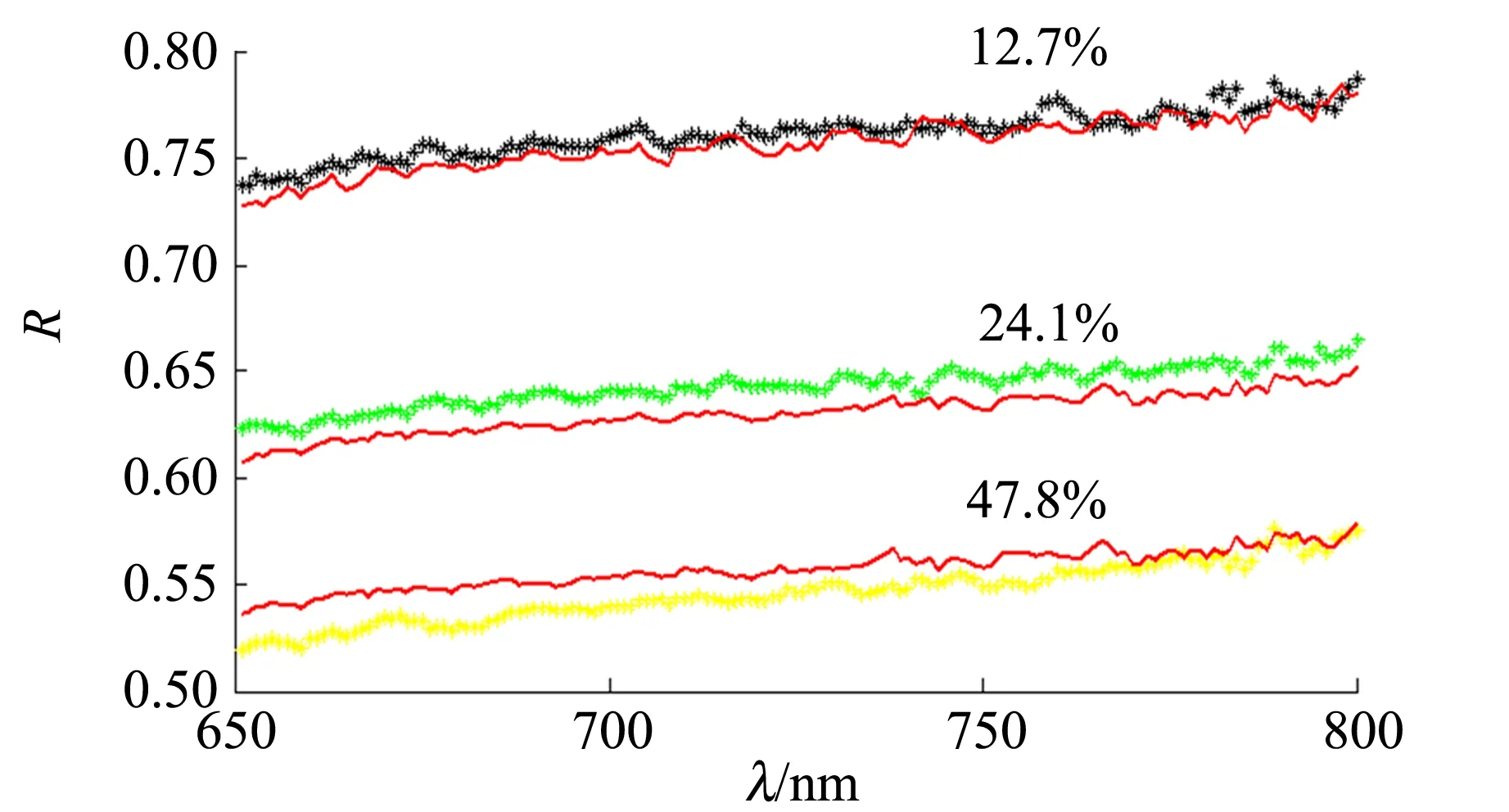
图5 反射率测量值和计算值对比

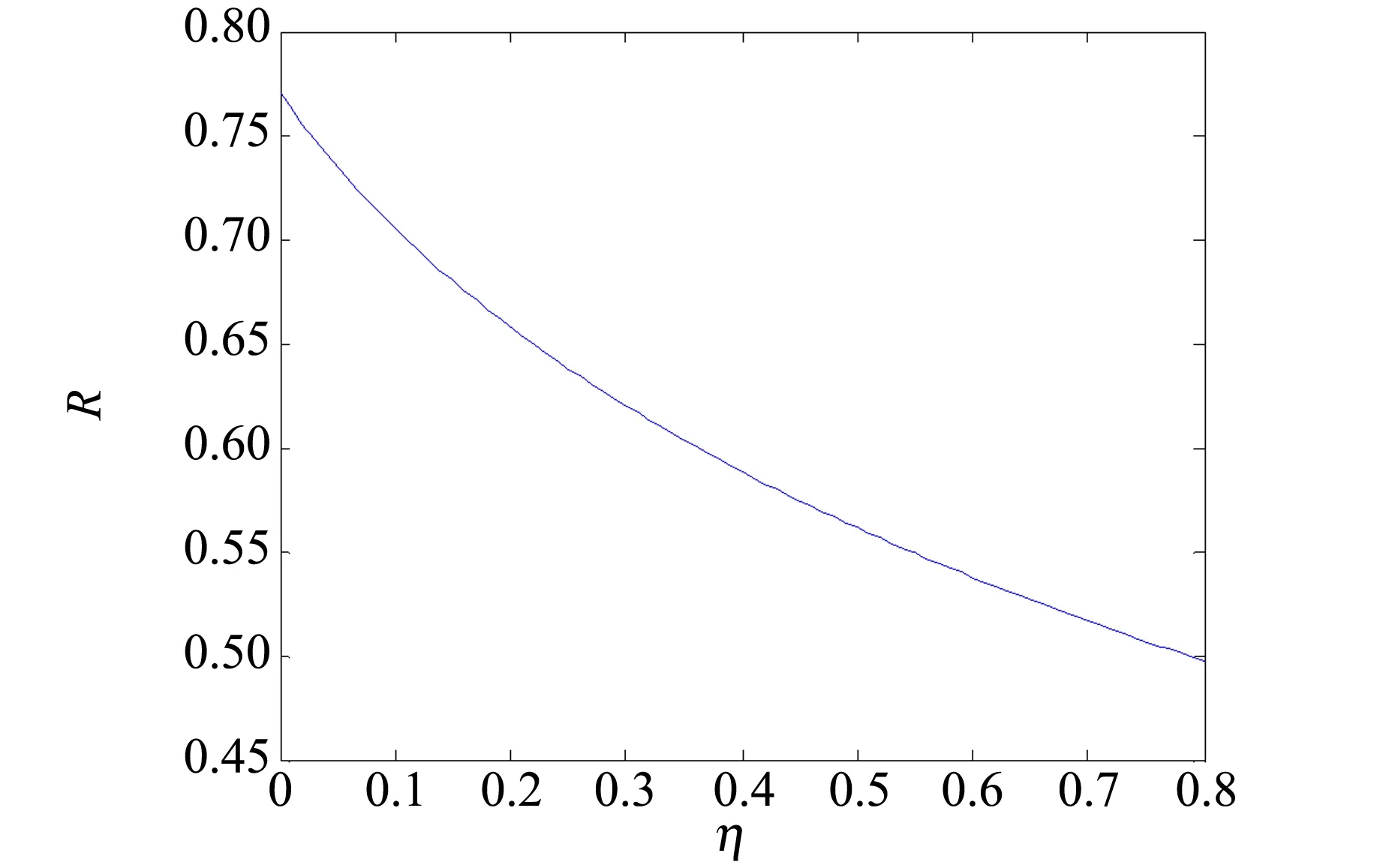
图6 700 nm波长时纤维表面反射率和潮湿程度关系

3 观察角度对潮湿变暗现象的影响

在上述讨论中，纤维反射率包括纤维在各个方向的反射光. 但是在实际生活中，纤维在各个方向的反射光并非均匀分布，因此观察角度的不同也会引起人眼明暗感觉的变化.

纤维织物表面满足朗伯发射体[6-7]，纤维织物表面的反射光强随观察角度的变化关系[8]为

I(θ)=I0cosθ,

(13)

其中I0为垂直表面方向的反射光强. 对于红色纤维，同样给出650～800 nm波段入射光下潮湿程度为24.7%的红色纤维的反射率随观察角度的变化关系, 如图7所示. 由图7可以看到，在光入射方向，光反射率达到最大值. 因此，对于湿润纤维，相比正视，人眼在斜视时观察到的衣物变暗现象更为明显.

图7 反射率随观察角度变化关系

4 结束语

从镜面反射与漫反射出发，推导了纤维潮湿程度和反射率之间的关系，并利用积分球自搭装置，实验定量测定了二者的关系，理论与实验符合. 研究表明：纤维的湿润程度与纤维表面的反射率负相关. 观察角度对潮湿衣物变暗的明暗效果影响明显. 但实际情况中，纤维湿润后不仅亮度会发生改变，色调和饱和度也会有微小的变化，这与介质和液体的色散性质有关，今后将在这方面继续开展研究.

[1] 张俊华，孟庆国. 衣物在潮湿时变暗的光学分析[J]. 物理实验，2016,36(1):31-34.

[2] Lekner J, Dorf M C. Why some things are darker when wet [J]. Applied Optics, 1988,27(7):1278-1280.

[3] 于助,刘国华,邹利君,等. 光强对比法测量表面粗糙度的研究[J]. 哈尔滨科学技术大学学报,1990,14(3):278-284.

[4] 姚启钧. 光学教程[M]. 北京：高等教育出版社,2002:159.

[5] 邱雁. 漫反射光谱的理论与应用研究[D]. 上海：同济大学,2007.

[6] Sirikasemlert A， Tao X. Effects of fabric parameters on specular reflection of single-jersey knitted fabrics [J]. Textile Research Journal, 1999,69(9):663-675.

[7] 石风俊. 织物漫反射光分布曲线的模拟计算[J]. 西北纺织工学院学报,2001,15(4):65-69.

[8] 刘全慧. 为什么入射波和散射波间的干涉不能忽略[J]. 大学物理，1999,18(7):11-12.

[责任编辑：任德香]

sini1=n21sini2.

Optical analysis of darkened wet clothes

FENG Yu, WANG Guang, ZHAO Min, LI Fo-sheng

(School of Physics Science and Engineering, Tongji University, Shanghai 200092, China)

The physical mechanism of clothes darkening after wet was analyzed theoretically. The reflectivity of wet medium under different conditions was derived by Hubelka-Munk equations. The relationship between water content and reflectivity was measured by integrating sphere. The result showed that the main reason of wet clothes being dark was a change of clothes scattering and absorption, and it was a negative correlation between the clothes humidity and reflectivity.

reflectivity； scattering rate; absorption rate; diffuse reflectance; integrating sphere

2017-04-25

冯 禹(1995-)，男，甘肃庆阳人，同济大学物理科学与工程学院2013级本科生.

赵 敏(1975-)，女，山东东阿人，同济大学物理科学与工程学院高级工程师，博士，从事物理演示实验教学工作.

O43

A

1005-4642(2017)08-0036-04