基于改进的层次分析法对高职学生创新能力的评价

胡 芬

(长江职业学院，武汉 430074)

基于改进的层次分析法对高职学生创新能力的评价

胡 芬

(长江职业学院，武汉 430074)

随着高职教育的发展，培养适应社会需求的创新型高技能型人才已成为高职院校的重要任务。以长江职业学院的学生为调查研究对象，利用改进的层次分析法对高职学生的创新能力进行分析与评价。通过定性和定量的分析客观的把握高职学生创新能力的特点，有利于高职院校的教师有针对性的进行教育教学改革，从而推动创新型人才的培养。

创新能力；高职学生；改进的层次分析法

随着我国走新型工业化道路、建设社会主义新农村和创新型国家对高技能人才要求的不断提高，高职教育在高等教育中的地位越来越重要。这对高职院校来说既是极好的机遇，也是巨大的挑战。21世纪的中国教育将以培养学生的创新精神和创新能力为核心和重点，这也是高职院校适应时代发展的必然要求。创新能力的培养是一个系统工程。对高职学生的创新能力进行分析和评价，不仅能够客观的把握高职学生创新能力的特点，同时也有利于高职院校的教师有针对性的进行教育教学改革，从而推动创新型人才的培养。

一、改进的层次分析法模型

(一)层次分析法的一般步骤

步骤1 建立层次分析结构模型

深入分析实际问题，将有关因素自上而下分层(目标—准则或指标—方案或对象)，上层受下层影响，而层内各因素基本上相对独立。

步骤2 构造判断矩阵

元素之间两两对比，对比采用美国运筹学家A.L.Saaty教授提出的1～9比率标度法(表1)对不同指标进行两两比较，构造判断矩阵。

表1 1～9标度的含义

设要比较各准则1,2,…,n对目标O的重要性，记判断矩阵为A。

步骤3 计算权向量并作一致性检验

由判断矩阵计算被比较元素对于该准则的相对权重，并进行一致性检验，若通过，则最大特征根λ对应的特征向量做为权向量。

一致性指标：

CI越大，不一致性越严重。

随机一致性指标：随机产生多个矩阵，将每个矩阵的一致性指标相加然后取平均值得到RI(见表2)。

表2 Saaty的随机一致性指标

注：表2中的n表示成判断矩阵的维数

步骤4 计算组合权向量(作组合一致性检验)

通过了一致性检验的矩阵，计算的总权重是可以确认的，否则说明判断矩阵中的一些信息元素仍存在着较大的偏差，需对判断矩阵进行调整。

(二)改进的层次分析法

改进的层次分析法是利用最优传递矩阵的概念，对层次分析法进行改进，使之自然满足一致性要求，直接可求出权重值，不需要进行一致性检验。

改进的层次分析法的步骤：

步骤1 建立层次分析结构模型；

步骤2 构造判断矩阵A，并利用最优传递矩阵的概念对判断矩阵A进行计算，公式如下：

步骤3 计算权向量；

步骤4 计算组合权向量。

二、高职学生创新能力的综合评价模型

(一)高职学生创新能力的评价结构

高职学生的成绩差异较大，导致其创新能力的因素复杂，需要从多角度、多层次来分析和建立评价指标体系，才能科学准确地反映出高职学生创新能力水平。本文选取了长江职业学院2016级财会金融学院、机电汽车学院和旅游信息学院计算机专业的学生作为调查研究的对象。根据当前对高职学生的培养目标，通过查阅相关资料并结合我校学生的特点，在遵循科学性、全面性、可操作性原则下，本文建立了适合高职学生特点的创新能力的评价指标体系(见表3)。该体系以高职学生的创新能力为总目标，从创新知识学习能力、创新个性、创新意识和创新实现能力四个方面的指标进行分析和评价。同时根据层次分析法的原理，将四个一级指标分解成24个二级指标，并将24个二级指标设计成问卷进行调查统计。

表3 创新能力指标

(二)高职学生创新能力各级权重的计算

权重是指某一项指标因素对高职学生创新能力影响的程度。权重的大小通常与影响程度成正比，权重值在0～1之间，所有评价因素的权重之和为1。确定权重的方法有多种，本文结合高职学生的特点，通过查阅相关文献构造判断矩阵，然后利用改进的层次分析法计算权重。改进的层次分析法是利用最优传递矩阵的概念，对层次分析法进行改进，使之自然满足一致性要求，直接可求出权重值，不需要进行一致性检验。利用美国运筹学家A.L.Saaty教授提出的1～9比率标度法(表1)对不同指标进行两两比较，构造判断矩阵。

创新能力的判断矩阵A如下：

四个一级指标的判断矩阵分别记为A1、A2、A3、A4，其对应的判断矩阵如下：

利用改进的层次分析法对上述5个判断矩阵进行计算，我们得到了高职学生创新能力各指标的权重。

创新能力的判断矩阵A对应的权重向量为：

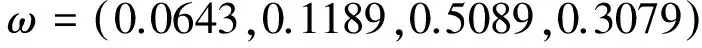
四个一级指标的判断矩阵A1、A2、A3、A4对应的权重向量分别为：

ω1=(0.0843,0.2381,0.1534,0.4812,0.0430)；

ω2=(0.1907,0.0675,0.1166,0.5836,0.0416)；

ω3=(0.1381,0.0354,0.0577,0.4583,0.3106)；

ω4=(0.1147,0.0517,0.0689,0.0319,0.02375,0.0219,0.3700,0.0517,0.0517)

最后通过计算组合权重得到24个二级指标在创新能力中所占权重如表4。

表4 24个二级指标的权重

三、高职学生创新能力的实证分析

本次问卷采用网络问卷方式进行，共有150人参与测试。参与问卷的对象按性别统计，男生102人(占68%)，女生48人(占32%)；按专业统计，机电专业有36人(占24%)，财会金融专业有29人(占19.3%)；旅游信息管理学院计算机专业有85人(占56.7%)。

对问卷统计得到的数据进行处理和计算，并通过改进的层次分析法得到的各指标的权重进行计算。

根据问卷统计的数据按性别计算24个指标的平均得分结果如图1。

图1 按性别统计各指标的平均得分

再利用统计得到的各指标的平均数和指标的权重计算可得，高职女生创新能力的最终综合得分为1.6672，高职男生创新能力的最终综合得分为1.8970。由此可知，高职学生的创新能力都介于1于2之间，即介于一般和良好之间，且男生的创新能力高于女生，接近良好。从图1也可以看出，除了对专业课的态度(指标2)、综合学习能力(指标5)和解决问题的态度(指标18)这三个方面女生较优于男生，其他方面女生均略低于男生。

根据问卷统计的数据按专业计算24个指标的平均得分结果如图2。

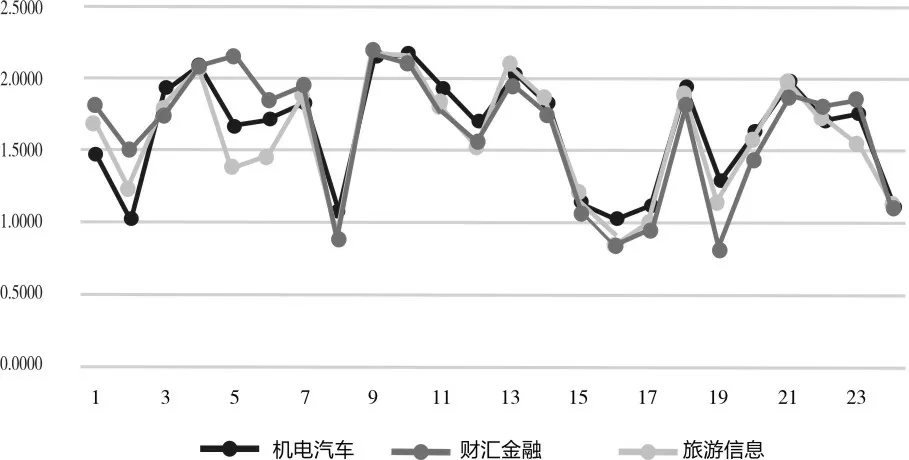
图2 按专业统计各指标的平均得分

同理计算得到高职机电汽车专业、财会金融专业、旅游信息学院计算机专业创新能力的最终综合得分分别为：1.8619、1.8904、1.8703。由此可知，高职学生各专业的创新能力比较接近，其中财会金融专业学生的创新能力要略优于另外两个专业的学生。

[1] 袁贵仁．不断推进教育创新[J]．北京师范大学学报(人文社会科学版)，2002(6).

[2] 吴祈宗．系统工程[M]．北京:北京理工大学出版社，2006.

[3] 涂恒汉．创新教育评价[M]．上海：东方出版社，2001.

[4] 彭健伯,等．应用型人才创新能力培养与创新能力测评方法研究[J]．科技进步与对策，2006(1).

[5] 李斯怡．高职院校大学生创新素质的现状及培养途径研究[J]．商品与质量: 理论研究，2011(SB).

Evaluating Innovative Ability of Vocational College Students Based on Improved Analytic Hierarchy Process

Hu Fen

(ChangjiangPolytechnic,Wuhan430074,China)

With the development of higher vocational education, it is clear that cultivating innovative talents has become a important task for colleges. The paper takes Changjiang Polytechnic students as an example, it tries to use improved analytic hierarchy process and evaluates the innovative ability of vocational students. Through the qualitative and quantitative analysis of vocational students' innovative ability, it is beneficial for teachers to carry out the reform of education and teaching so as to promote the cultivation of innovative talents.

Innovative ability; vocational students; improved analytic hierarchy process

G712

A

1673-3878(2017)04-0068-04

2017-05-06

胡芬(1982-)，女，湖北天门人，硕士，长江职业学院讲师；主要研究方向：数理统计、高职教育.