大型引水工程规划设计阶段高程控制测量方法探讨

肖文全，段陈君

(1.四川省水利水电勘测设计研究院，成都，610500；2.四川蜀禹水利水电工程设计有限公司，成都，610072)



大型引水工程规划设计阶段高程控制测量方法探讨

肖文全1，段陈君2

(1.四川省水利水电勘测设计研究院，成都，610500；2.四川蜀禹水利水电工程设计有限公司，成都，610072)

水利工程引水线路受交通、地形条件的限制，全部采用水准测量的方式来完成高程控制的难度较大。本文结合实际工程，对高程曲面拟合的原理、步骤进行了阐述，并利用不同的高程拟合方法，与省大地水准面模型精化后的部分控制点得到的高程进行比较，得出采用水准联测拟合方法可满足工程设计的需要的结论。

GPS高程 水准高程 曲面拟合

1 引言

目前高程控制测量一般采用水准测量、三角高程测量、GPS拟合高程等方法，对于大型水利工程的引水渠道而言，水准测量精度高，但由于地形及交通条件限制，需要投入的时间、人力和物力较大；三角高程测量要求的相对高差有限制，水利工程大多地处山区或丘陵，三角高程的施测难度较大且精度难以达到；单一的GPS高程拟合不受地形、通视等条件的限制，但对大型带状测区精度不可控，这三种独立的方式都不适合大型引水工程的带状测区。

2 原理和方法

当一测区内有一定数量点的平面坐标和高程已知，按坐标转换原理，求出参考椭球面与似大地水准面之间的平移与旋转参数，把这些参数加入GPS网平差，在已知点高程约束下，在求出GPS点平面坐标的同时，求出点的正常高[1]。

为了求得测区范围内的高程异常分布函数，需要在测区内对高程异常分布建立函数[2]。拟合精度与模型有很大的关系，如地形平坦地区适合采用平面相关拟合，而在高程异常变化剧烈的地区通常采用曲面拟合，此时重合点要选在高程异常变化较大的转角处，且应适当增加重合点数量[3]。如果遇到测区面积很大的情况，那么可以采用分区拟合的方法[4]。

基于上述情况，经过多方研究与对比，决定采用国家高等级水准点对部分控制点进行三等水准联测，再采用联测后的水准高程进行曲面拟合的综合法进行施测及计算。将计算结果同省测绘局通过精化后的四川省大地水准面模型计算的部分控制点成果进行比较，检验是否满足工程需要，通过采用不同方法得到的结果进行对比分析，得出采用该方法的合理性及可行性。

3 应用与分析

以亭子口水利工程总干渠为例，通过平面平移法、曲面拟合法计算结果与部分测绘局经大地水准面模型精化后的点的高程进行对比分析，两种拟合方法的计算均在POWERADJ4.0软件中进行。

3.1 工程概况及任务要求

亭子口水利枢纽工程位于四川省苍溪县境内，是嘉陵江干流唯一具有较好调节性能的以防洪、灌溉及城乡供水为主，兼顾发电、航运，并具有拦沙减淤等作用的大型综合水利工程。亭子口灌区涉及广元市、南充市、广安市和达州4市12县(市、区)，幅员面积8489.5km2，范围为：北起苍溪县浙水乡，南抵重庆合川市界，西至嘉陵江，东以仪陇河、流江河、渠江为界，以及嘉陵江右岸白溪河与引水渠线之间的部份区域。该项目涉及的引水线路普遍处于上述区域中高程较高的地方，交通相对落后，地形复杂，相对高差较大的深丘或高山地区，控制测量和地形测量的难度都比较大。

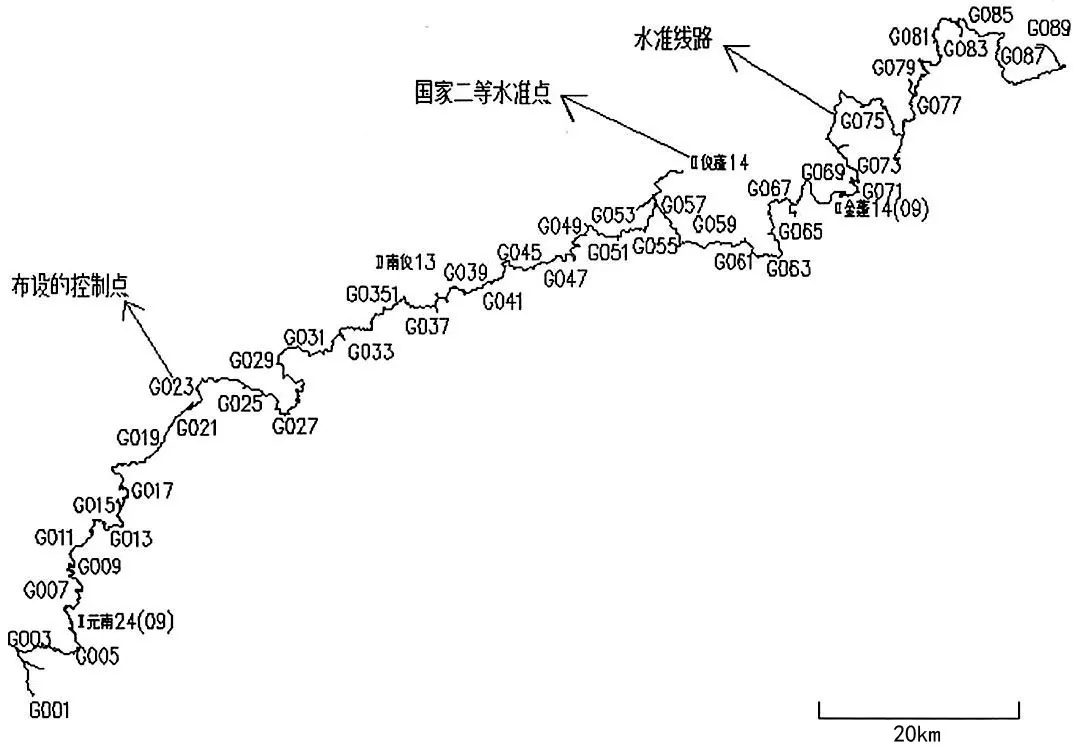
图1 控制网点及水准线路示意

图1为测区控制网点及水准线路示意图，水准线路为设计的控制网中每点均进行水准测量的水准线路图，其中包含了采用三等水准联测部分国家高等级水准点的线路，“Ⅱ仪蓬”等为国家二等水准点大致位置，该干渠共布设控制点(平面及高程共用)90点。以下示例中数据均经过脱密处理。

根据设计合同约定的时间，总干渠约140km的控制测量要求在30d内完成，平面控制测量采用GPS施测，效率较高，但高程控制测量按常规需进行四等水准测量。据统计，如果控制网中每点均进行水准测量，水准往返测线路的长度约为657km，且绝大部分地区相对高差较大，以2km测段为例，平均高差约50m，最大高差约110m，将投入大量的人力和物力，各方面成本极高。如果采用三等水准联测部分离国家高等级水准点较近的部分控制点作为固定点进行高程的曲面拟合，以联测网中9个点为例，水准线路往返测长度约为107km，水准测量的工作量将缩减80%以上。

3.2 平面平移法

平面平移法是指以控制网中某一点作为固定点，其它点均作为未知点，不加入任何模型改正的一种GPS拟合方式，在控制点稀少且高程异常变化平缓的区域或联测水准有困难的情况下，可以使用GPS高程平面拟合的方法代替四等水准[5]。

在该网中采用G005作为固定点进行拟合计算。计算书如表1(由于数据量较大，案例中仅选取了部分控制点作为示例)。

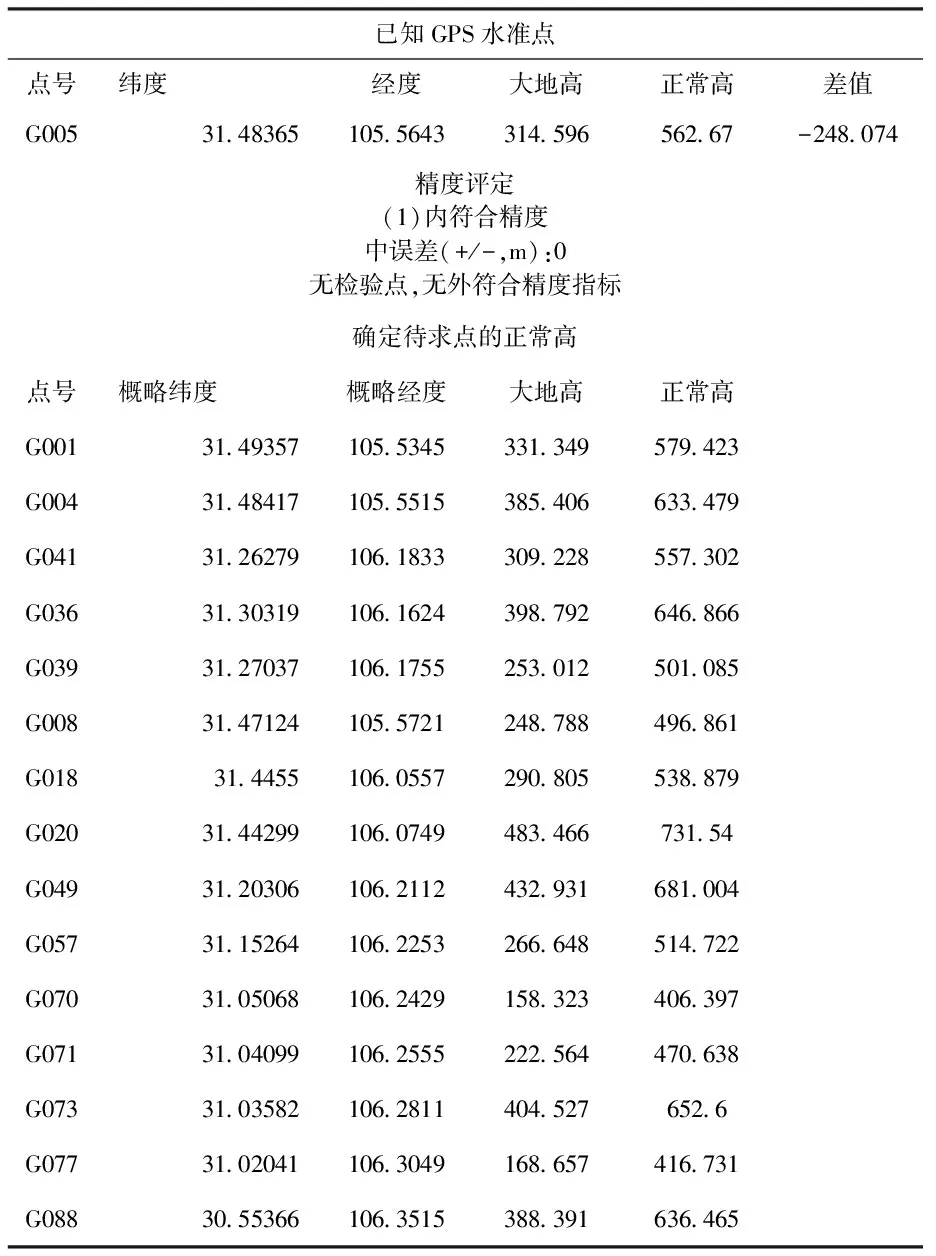
表1 平面平移法GPS高程计算结果

由表1可以看出，平面平移法拟合高程无校核及约束条件，误差累积无法消除，类似于支导线，不适合规模较大的控制网。

3.3 曲面拟合法

GPS曲面拟合法是用于GPS点分布在一定区域的时候，且可以选择数学曲面拟合似大地水准面，构造适当的数学模型，计算高程异常值，然后求出正常高。具体的思想是：已知测区的若干水准点，并用GPS测算这些点的高程，利用公式求得这些点的高程异常，利用已知点平面坐标(x，y)和高程异常值构造数学模型拟合最为接近于该测区的似大地水准面，进而求出正常高。GPS点高程异常拟合的精度主要取决于所采用的数学平面或数学曲面与似大地水准面拟合程度[6]。GPS水准高程拟合的精度主要受拟合似大地水准面、已知点高程和GPS网点的大地高三种误差影响[7]。

在本工程中，部分GPS点采用水准测量方法联测国家水准点，得到以下GPS点的水准高程，再将其作为固定点进行曲面拟合。计算结果见表2。

表2 曲面拟合法GPS高程计算结果

从表2及图1可以看出，经过水准联测的控制点均匀分布在线状工程中，有利于提高曲面拟合精度，减小高程异常的影响，在地势比较平坦且点位分布均匀、数量足够的区域，运用拟合法把大地高转化为GPS水准高能达到四等几何水准精度[8]。

经过平差软件处理后，外部检核点G041水准高程557.394m，高程拟合计算所得正常高557.384m；G071水准高程470.977m，高程拟合计算所得470.979m。经过比较G041相差10mm，G071相差2mm，满足工程要求。

3.4 结果的对比分析

将上述两种拟合方式的结果与经省大地水准面模型精化后的控制点成果进行比较，结果见表3。

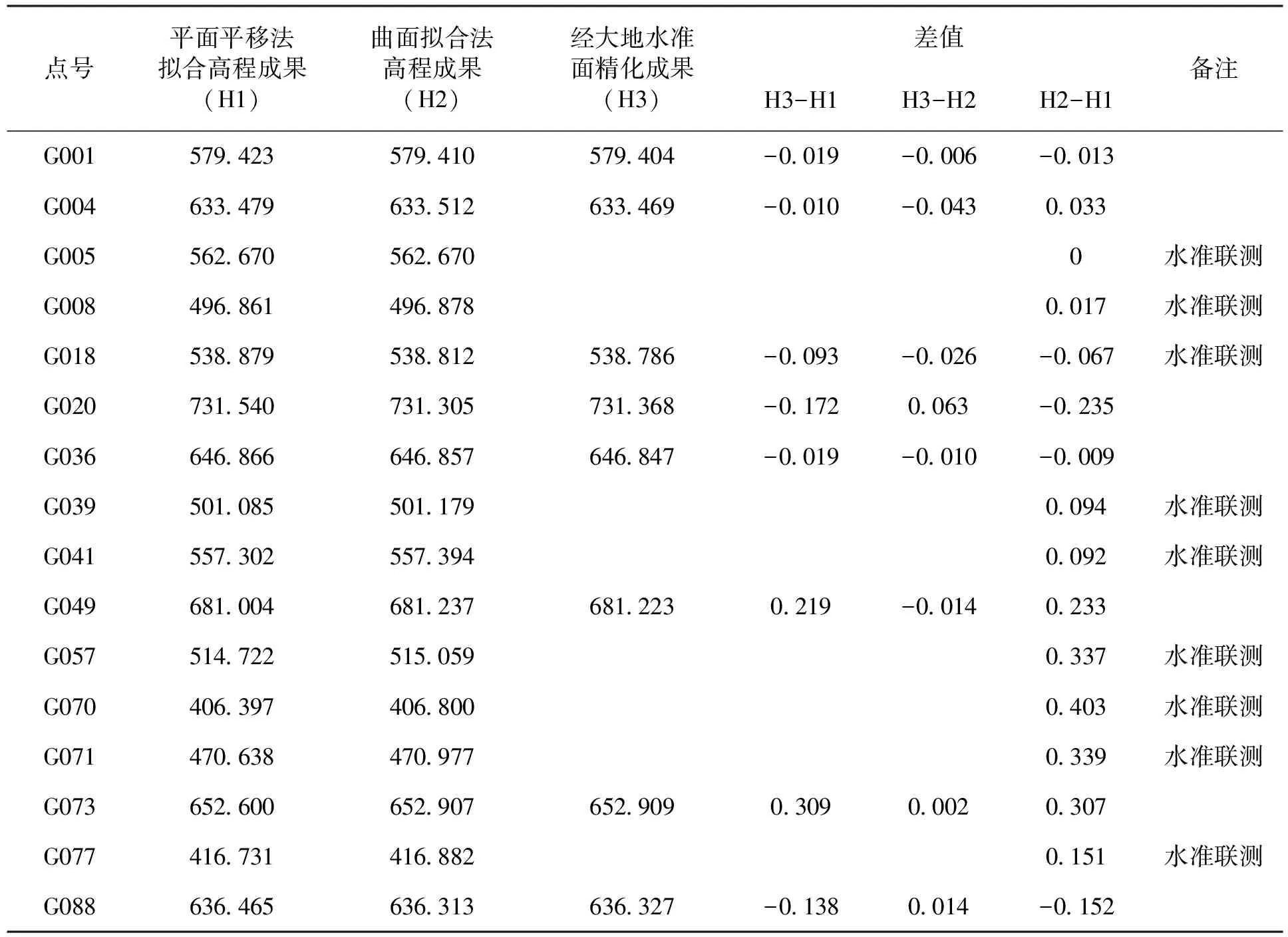
表3 不同计算方法成果比较表

从上表3可以看出，平面平移法成果与经大地水准面模型精化后的成果比较，最大差值为0.309m，平均差值为0.122m，差值较大，不能满足工程要求；通过水准联测的控制点进行曲面拟合的成果与精化成果进行比较，最大差值为0.063m，平均差值为0.022m，满足工程设计规划阶段的需求。

4 结论

在山区狭长带状工程中，水准测量不稳定因素太多，偶然误差或者粗差概率较大。选取部分控制点联测国家高等级水准点，再进行高程拟合的方式进行高程控制测量，既能满足工程的要求，又能节约工期节约成本，不失为一种简单有效的方法。结合工程实际情况，采用局部点联测国家高等级水准点，进行曲面拟合所得到的高程，不仅能够满足工程需要，还能缩减80%以上的水准测量工作量，节约了大量工期及成本，在实际工作中很有意义。

〔1〕牛延国.GPS高程水准拟合模型与精度分析[J].辽宁工程技术大学学报(自然科学版)，2008，27(1)：35-38.

〔2〕刘彦祥.GPS高程拟合在工程中的应用[J].水道港口，2012，33(6):536-539.

〔3〕孙茂存.浅谈线型带状工程的GPS高程拟合[J].科技风，2009(1):24.

〔4〕刘吉刚.GPS高程拟合[J].技术研发，2013(10):98.

〔5〕常红斌，苏 恒.GPS高程平面拟合法的应用[J].城市勘测，2014(4):101-103.

〔6〕郭英起，伊晓东，黄瑞金，等.狭长区域下基于正交法的GPS高程拟合研究[J].测绘工程，2007，16(6):19-21.

〔7〕马 迁，朱继文.GPS水准高程拟合精度分析[J].煤炭技术，2009，28(1)：150-152.

〔8〕欧阳玉华，阮 戟.GPS水准高程拟合模型选择及应用[J].地理空间信息，2008，6(6):26-28.

■

TV221.1∶P228.9

B

2095-1809(2017)04-0044-04