基于模数哥隆尺的新颖eALT-QC-LDPC码构造方法

2017-08-16李玲香李季碧邵金侠

重庆邮电大学学报(自然科学版) 2017年4期

李玲香，李季碧，邵金侠

(1.湖南科技学院电子与信息工程学院，湖南永州，425199；2. 重庆邮电大学通信与信息工程学院，重庆 400065；3.湖南科技学院电子与信息工程学院，湖南永州，425199)

基于模数哥隆尺的新颖eALT-QC-LDPC码构造方法

李玲香1，李季碧2，邵金侠3

基于模数哥隆尺, 提出一种扩展近似下三角阵结构的准循环低密度奇偶校验(extending approximate lower triangular structure-quasi cyclic-low density parity check，eALT-QC-LDPC)码新颖构造方法，该方法无需计算机搜索即可完全消除长度为4，6，8的短环，通过设置不同的参数即可构造出多种码型。所提出的构造方法在确保线性编码复杂度前提下，大大改善了码字性能。仿真结果表明，所构造的码率0.66的eALT-QC-LDPC(5 913,3 952)码，码率0.63的eALT-QC-LDPC(3 648,2 289)，码率0.5的eALT-QC-LDPC(1 116,565)以及eALT-QC-LDPC(684,349)码的纠错性能比同码率码长度分布的渐进边增长(progress edge growth，PEG)码和围长至少为8的同码率码长的QC-LDPC码都得到了一定程度的改善。其中码率为0.5的eALT-QC-LDPC码与IS-GPS-800协议中随机构造的LDPC码误码率性能比较接近，但所构造的新eALT-QC-LDPC码编译码易实现，极大地降低了存储空间，对导航系统信道编码方案具有重要的参考价值。

准循环LDPC(QC-LDPC)码；模数哥隆尺；纠错性能；误码率(BER)

0 引言

低密度奇偶校验(low density parity check，LDPC)码是一类性能逼近香农信道极限的纠错码[1]。由于其编译码复杂度低、纠错能力强及应用前景广阔的特点，目前LDPC码已成为了编码理论界倍受瞩目的一个研究热点。准循环LDPC(quasi cyclic LDPC, QC-LDPC)码是基于循环置换矩阵的一种结构化LDPC码，它的校验矩阵由循环置换矩阵构成，能够获得比较低的线性编码复杂度、较低的错误平层以及性能优越的纠错能力，编码过程可通过简单移位寄存器来实现[2]。理论研究表明，随着LDPC码围长的增加，码间距离将以指数增长。M.P.C.Fossorier在文献[3]中给出了构造大环长QC-LDPC码的充分必要条件。目前，大多数围长大于6的QC-LDPC构造是基于高复杂度的计算机搜索[4]，或者是结合计算机搜索和代数构造[5-7]，而部分结构化QC-LDPC构造仅消除了4环[8-9]。因而，构造具有girth-8且性能优越的QC-LDPC编码已经成为其实用化的一个技术瓶颈。

针对上述问题，本文基于模数哥隆尺序列[10]的思想，提出了一种QC-LDPC码的新颖构造方法，应用该构造方法能构造出具有扩展近似下三角阵(extending approximate lower triangular，eALT)结构、易于实现编码且girth-10的eALT-QC-LDPC码。并且证明了基于该结构和模数哥隆尺所构造的QC-LDPC码的校验矩阵不存在8环。该方法所构造的QC-LDPC码是结构化代数构造的QC-LDPC码型，同时这种结构化的代数码型可以根据需要而灵活设计出不同码率码长的码字。仿真结果表明，该方法所构造的eALT-QC-LDPC码的纠错性能优于具有相同码率码长以及度分布的渐进边增长(progress edge growth，PEG)码。

1 模数哥隆尺

哥隆尺可以进行如下定义：假设一把尺子的最大刻度为z，称之为尺子的长度z，标识第一个刻度为0，尺子上刻度标识的总个数被称作该尺的阶，记作γ，如果尺子上两两刻度之间所度量的长度各不相同，那么就称这把尺子为哥隆尺。基于哥隆尺概念就可给出如下模数哥隆尺概念。

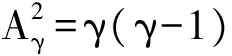
将模数哥隆尺的定义与辛格完备差集结合可得到定理1。

定理1 令z=pα是一个素数幂，则存在H个整数d0,d1,…,dγ-1使得有H个差集di-dj模(γ-1)2+(γ-1)+1所得的数为互不相同且小于(γ-1)2+(γ-1)+1的非0正整数。

2 一种新颖eALT-QC-LDPC码构造方法

基于不同阶数γ的模数哥隆尺序列，即哥隆尺上的刻度s0,s1,…,sγ-1，对此序列分析可知，模数哥隆尺序列为递增序列，且两两之间的差值各不相同。本文提出如图1所示的一种具有近似下三角阵eALT结构的原模矩阵E。原模矩阵的上半部分为γ个阵列Mi(0≤i≤γ-1)，下半部分为γ个方阵Ni(0≤i≤γ-1)，除了阵列Mi以及方阵Ni对角线上的元素bi,j(0≤j≤γ-1)为非负整数，其他空白处元素初始化为-1。设z为循环置换矩阵(circulant permutation matrix，CPM)的阶数。

该结构原模矩阵代数式表示为

(1)

进而将原模矩阵中非负元素用z×z的单位矩阵或其循环移位矩阵扩展，-1元素用z×z的全零矩阵扩展从而得到最终的校验矩阵H。

图1 eALT结构的原模矩阵EFig.1 Original matrix E of eALT structure

文献[3]中，M.P.C.Fossorier给出了QC-LDPC码具有2i环长的充分必要条件，如定理2所示。无需证明的是，若原模矩阵中存在c个2i的环，则经z阶循环置换扩展后得到的校验矩阵包含cz个2i的环。本文根据围长条件设计了围长至少为10的原模矩阵，构造方法简述如下。

1)Mi的第1行均设为0元素，第2行设为阶是γ的模数哥隆尺序列{s0,s1,…,sγ-1}，即γ个非负整数。注意，此处第2行若有多个序列随机选即可，若需要构造特定码率长码长，亦可以随机选取任意阶的模数哥隆尺序列的γ个，如表1中的eALT-QC-LDPC(3 856,969)码。

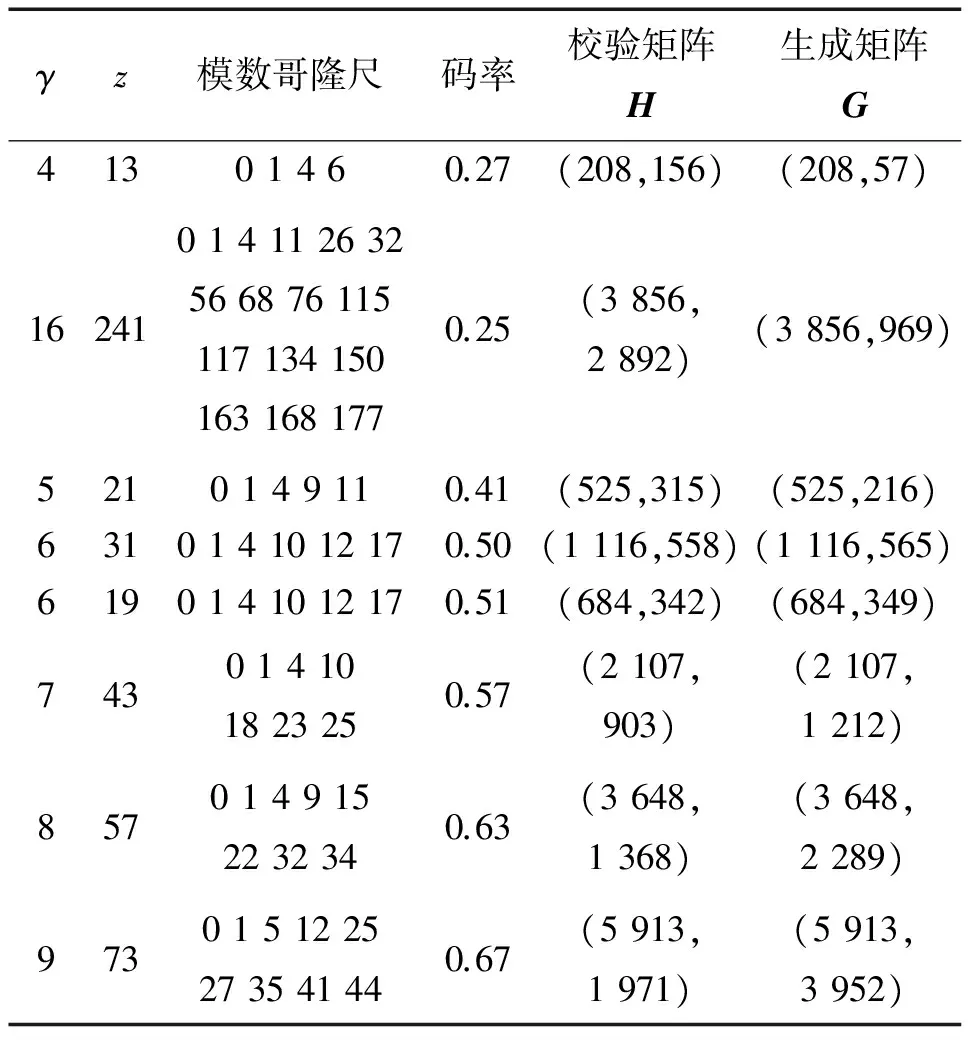
表1 各种码型参数Tab.1 Parameters of the various codes

2)设向量Vγ={v0,v1,…vi,vj,…,vγ-1}，且满足Vγ∩(1+Vγ)=φ，0<|vi-vj|≤z-1。Ni的主对角线上元素，依次设为{vi×s0,vi×s1,vi×s2,…,vi×vγ-1}(modz)，最简单地，选取Vγ={1+2×0,1+2×1,…,1+2×(γ-1)}或者Vγ={2×0,2×1,…,2×(γ-1)}。

3)继而，对上述构造的eALT原模矩阵进行z阶循环置换矩阵扩展得到最终的校验矩阵H，一般选取扩展因子z满足z>smax，的整数即可，本文直接采用模数哥隆尺的模数z。

显然通过选取不同的参数γ，z以及模数哥隆尺序列，可以灵活构造多种码长、码率的码型，表1中列举了本文构造的码型。具体构造方法示例如图2所示，选取γ=6，Vγ={1+2×0,1+2×1,…,1+2×(γ-1)}。

图2 γ=6的eALT结构的原模矩阵EFig.2 Original matrix E with eALT structure at γ=6

定理2 设(a1,a2,…,a2l-1,a2l)是原模矩阵E中的序列，设ai和ai+1在同一行或者在同一列，而ai和ai+2在不同行且不同列，若存在最小正整数r使(2)式成立。

(2)

则序列(a1,a2,…,a2l-1,a2l)构成校验矩阵H中长度为2lr的环。由此可通过对原模矩阵E的检测来确定校验矩阵H中是否存在某个长度的环，鉴于原模矩阵E的尺寸相对于校验矩阵H的尺寸是很小的，可以对原模矩阵E检测以确定校验矩阵H中是否存在某个长度的环，工作量大大降低的同时也利于消除校验矩阵中的短环。

基于Fossorier定理，长度2i的环中的2i个元素必然属于奇偶校验矩阵H中的i行i列，若把H映射到其相应的原模矩阵E中时，H矩阵中的一个长度2i的环需跨越E中的i行i列。显然，图3所示的eALT结构的原模矩阵不存在6环。

图3 原模矩阵中8环形式Fig.3 Girth-8 form in the original matrix

接下来将结合模数哥隆尺序列的性质证明所设计的eALT原模矩阵不存在4环或8环。

1)无4环证明。根据Fossorier定理以及本文设计的eALT原模矩阵结构，若存在4环，则必然分布在Mi中。而Mi的第1行是零元素，假设Mi的，列存在4环，则必有0-sI+sJ-0=0modz成立，而Mi的第2行是模数哥隆尺序列，两两元素互不相同。所以，上式不成立，故而所设计的原模矩阵不存在4环。

2)无8环证明。若存在8环，则必然不会独立存在于Mi或者Ni，那么所设计的原模矩阵中8环形式必然如图3所示，显然，该形式8环分为4种情况。

情况①Mi(1,t)→Mi(1,k)→bi,k→bj,k→

Mj(1,k)→Mj(1,t)→bj,t→bi,t

情况②Mi(2,t)→Mi(2,k)→bi,k→bj,k→

Mj(2,k)→Mj(2,t)→bj,t→bi,t

情况③Mi(1,t)→Mi(1,k)→bi,k→bj,k→

Mj(2,k)→Mj(2,t)→bj,t→bi,t

情况④Mi(2,t)→Mi(2,k)→bi,k→bj,k→

Mj(1,k)→Mj(1,t)→bj,t→bi,t

基于Fossorier定理，若存在情况①的8环，则有Mi(1,t)-Mi(1,k)+bi,k-bj,k+Mj(1,k)-Mj(1,t)+bj,t-bi,t=0modz)，进而得到visk-vjsk+vjst-vist=0(modz)即(vi-vj)(sk-st)=0(modz)，由模数哥隆尺序列性质易知(sk-st)≠0(modz)，并且0<|vi-vj|≤z-1，必有(vi-vj)≠0(modz)，所以情况①的8环不存在；情况②的8环等价于式子Mi(2,t)-Mi(2,k)+bi,k-bj,k+Mj(2,k)-Mj(2,t)+bj,t-bi,t=0(modz)成立，进而得到st-sk+visk-vjsk+sk-st+vjst-vist=0(modz)即(vi-vj)(sk-st)=0(modz)，与情况①相同；情况③的8环等价于Mi(1,t)-Mi(1,k)+bi,k-bj,k+Mj(2,k)-Mj(2,t)+bj,t-bi,t=0(modz)成立，进而得到visk-vjsk+sk-st+vjst-vist=0(modz)，即(1+vi-vj)(sk-st)=0(modz)，因为∩Vγ∩(1+Vγ)=∅，所有必有(1+vi-vj)≠0(modz)；而情况④与情况③类似。

综上所述，本文所提出的基于模数哥隆尺的eALT结构原模矩阵不存在8环，即消除了长度为4，6和8的短环，围长至少是10。

3 仿真性能分析

在由本文所提出的构造方法所构造的新颖eALT-QC-LDPC码型进行译码仿真时，采用对数似然比置信传播(log-likelihood-ratio belief-propagation, LLR-BP)译码算法，仿真环境为信道采用加性高斯白噪声信道(additive white gaussian noise, AWGN)，调制方式是二进制相移键控(binary phase shift keying, BPSK)，最大迭代次数设为60。从表1中列举的码型参数可以看出，设置不同参数可构造多种LDPC码型。为充分衡量新构造的LDPC码的性能，选用具有相同的码长码率及度分布的随机PEG码以及文献[11]中围长至少为8的同码率码长的QC码作为对比曲线，在码率为0.5时，与IS-GPS-800协议[12]中构造的随机LDPC码作了对比。

例1 选取阶为γ=6的哥隆尺序列{0,1,4,10,12,17}，Mi={0,0,0,0,0,0},{0,1,4,10,12,17}，Vi={1,3,5,7,9,11}，依据Mi中的序列计算出相应的Ni的主对角线元素，扩展因子分别选取z=31以及z=19，从而构造出校验矩阵H(1 116,558)以及H(684,342)，其零空间分别给出码字eALT-QC-LDPC (1 116,565)，以及eALT-QC-LDPC (684,349)，码率为0.5。与PEG随机码以及文献[11]中提出的围长至少为8的同码率码长的QC码误码率(bit error rate, BER)性能对比曲线如图4所示，其中，R为码率。同时，与IS-GPS-800协议中码率为0.5，随机构造的LDPC码的BER性能作了对比，如图5所示。

由图4的仿真结果分析表明，利用本文所提出的围长至少为10的新颖构造方法所构造的eALT-QC(1 116,565)码以及eALT-QC(684,349)码较PEG码在BER=10-5时，BER性能约有0.29 dB的提升，较文献[11]中的girth-8-QC-LDPC(1 116,560)码在BER=10-5时，eALT-QC(1 116,565)码约有0.5 dB的提升，eALT-QC(684,349)码较girth-8-QC-LDPC (684,344)码，在BER=10-5时，约有0.70 dB的提升。本文所构造的eALT-QC-LDPC码之所以能提升其纠错性能，是因为本文所提出的新颖构造方法消除了长度为4，6和8的短环，其围长至少为10，有效地解决了码长较短而导致其BER性能较差的问题。由图5的仿真结果分析可知，本文所构造的eALT-QC-LDPC码与IS-GPS-800协议中随机构造的LDPC码BER性能极其接近，但本文构造的eALT-QC-LDPC码编译码易实现，只需存储一串哥隆尺序列，极大地降低了存储空间。

图4 本文所构造的码率为0.5的eALT-QC-LDPC码与 PEG随机码以及文献[11]中LDPC码的性能对比Fig.4 Contrast figure of the error-correction performances among the constructed eALT-QC-LDPC codes with the code-rate of 0.5 in this paper, the PEG random codes and the LDPC codes in reference[11]

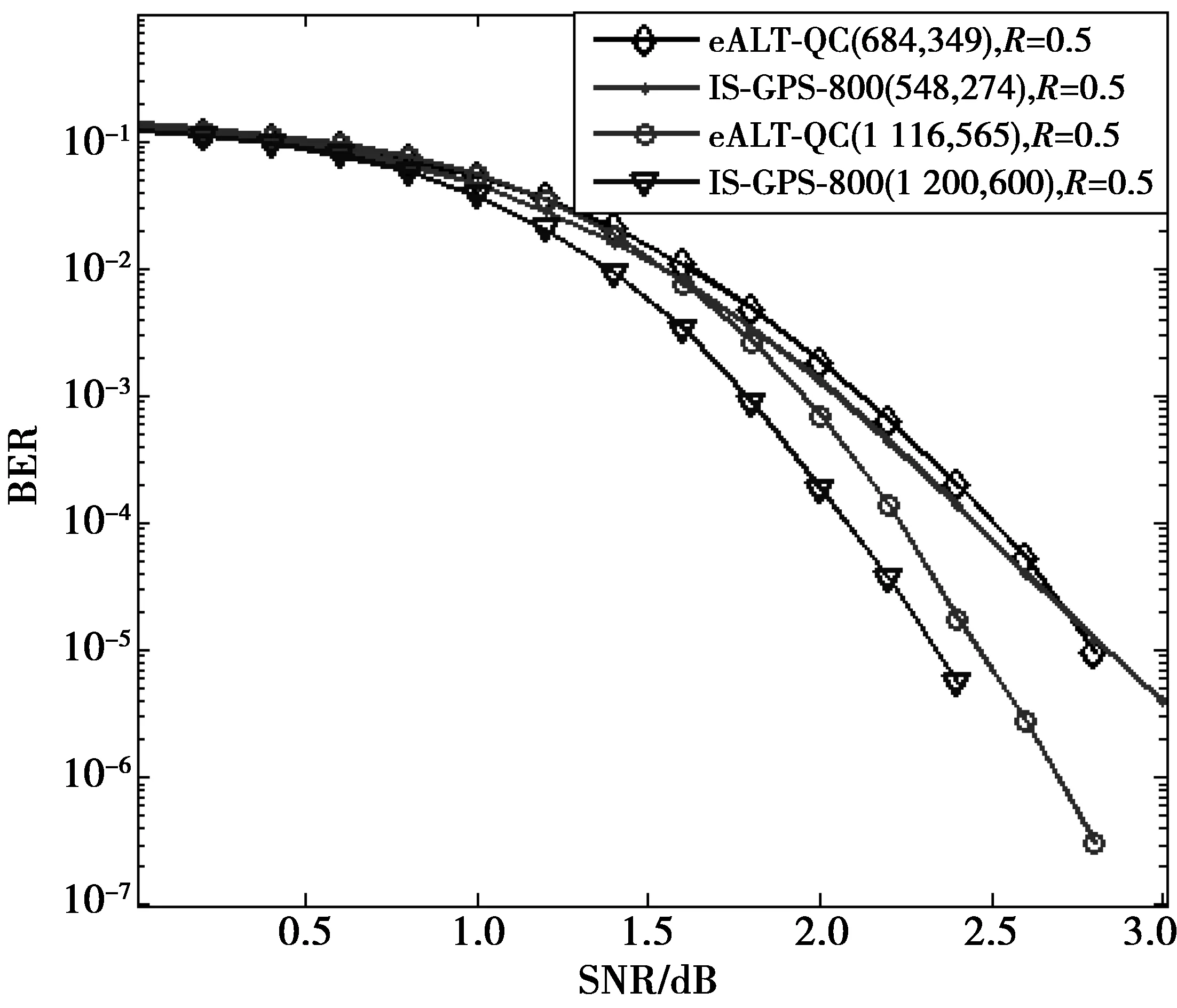
图5 本文所构造的码率为0.5的eALT-QC-LDPC码与 IS-GPS-800中随机LDPC码性能对比Fig.5 Contrast figure of the error-correction performances among the constructed eALT-QC-LDPC codes with the code-rate of 0.5 in this paper and the random LDPC codes in IS-GPS-800 Protocol

例2 选取阶为γ=8的哥隆尺序列即Mi={0,0,0,0,0,0,0,0},{0,1,4,9,15,22,32,34}，依据Mi中的序列计算出相应的Ni的主对角线元素，扩展因子选取z=57，从而构造出校验矩阵H(3 648,1 368)，其零空间给出码字eALT-QC-LDPC(3 648,2 289) 码，码率为0.63；选取阶为γ=9的哥隆尺序列{0,1,5,12,25,27,35,41,44}，Mi={0,0,0,0,0,0,0,0,0},{0,1,5,12,25,27,35,41,44}，Vi={1,3,5,7,9,11,13,15,17}，依据Mi中的序列计算出相应的Ni的主对角线元素，扩展因子选取z=73，从而构造出校验矩阵H(5913,1971)，其零空间给出码字eALT-QC-LDPC (5913,3952)，码率为0.67，其BER性能的对比曲线如图6所示。

图6 本文所构造的码率分别为0.63和0.67的 eALT-QC-LDPC码与其他LDPC码的性能对比Fig.6 Contrast figure of the error-correction performances among the constructed eALT-QC-LDPC codes with the code-rate of 0.63 and 0.67 in this paper and other LDPC codes

由图6的仿真结果分析表明，利用本文所提出的围长至少为10的新颖构造方法所构造的eALT-QC-LDPC(3 648,2 289)码在信噪比2.32 dB时，BER达到10-7，在BER=10-5时，性能优于随机PEG码约0.24 dB；eALT-QC-LDPC (5 913,3 952) 码在信噪比为2.2 dB时，译码收敛速度表现出了良好的瀑布特性，在BER=10-5时，性能优于PEG随机码约0.26 dB。分别与文献[11]中所构造的围长至少为8的同码率码长的girth-8-QC-LDPC码对比，在BER=10-6时，eALT-QC(3 648,2 289)码比girth-8-QC-LDPC(3 648,2 283)码约有0.22 dB的性能提升；在BER=10-5时，eALT-QC-LDPC (5 913,3 952)码比girth-8-QC-LDPC(5 513,3 944)约有0.62 dB的性能提升。这里进一步论证了利用本文所提出的围长至少是10的eALT-QC-LDPC码新颖构造方法能有效解决码长较短而导致其BER性能较差的问题，进而在一定程度上改善了eALT-QC-LDPC码的纠错性能，并且利用本文所提出的结构化构造方法所构造的eALT-QC-LDPC码大大降低了编译码复杂度。

4 结论

本文结合模数哥隆尺序列和QC-LDPC结构化的编码思想，提出了一种围长至少是10的eALT-QC-LDPC码新颖构造方法，该构造方法能构造出具有扩展近似下三角阵结构、易于实现编码且girth-10的eALT-QC-LDPC码。仿真结果分析表明，利用本文所提出的围长至少是10的新颖构造方法所构造的eALT-QC-LDPC码比文献[11]中所构造的围长至少为8的girth-8-QC-LDPC码以及PEG随机码的纠错性能更好。这充分表明本文所提出的围长至少是10的新颖构造方法能有效解决码长较短而导致的BER性能差的问题。而例1中所构造的码率为0.5且码长较短的eALT-QC(1 116,565)码与eALT-QC(684,349)码与IS-GPS-800协议中随机构造的LDPC码的BER性能比较接近，但本文的构造方法只需存储一串哥隆尺序列，利用循环移位寄存器即可实现，大大降低了编码器与硬件实现的复杂度并减少了所需要的存储空间，因而适用于导航系统中的信道编码。

[1] TASDIGHI A,BANIHASHEMI A,SADEGHI M R.Efficient search of girth-optimal QC-LDPC codes[J].IEEE Transactions on Information Theory,2015,62(4):1552-1564.

[2] LI J, LIU K, LIN S, et al. Algebraic Quasi-Cyclic LDPC Codes: Construction, Low Error-Floor, Large Girth and a Reduced-Complexity Decoding Scheme[J]. IEEE Transactions on Communications, 2014, 62(8): 2626-2637.

[3] FOSSORIER M P C. Quasi-cyclic Low Density Parity Check Codes from Circulant Permutation Matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788-1793.

[4] WANG Y, YEDIDIA J S, DRAPER S C.Construction of high-girth QC-LDPC codes[C]//5th International Symposium on Turbo Codes and Related Topics. Lausanne, Switzerland: [s.n.], 2008,180-185.

[5] LI J, LIU K, LIN S, et al. Algebraic Quasi-Cyclic LDPC Codes: Construction, Low Error-Floor,Large Girth and a Reduced-Complexity Decoding Scheme[J].IEEE Transactions on Communications, 2014, 62(8):2626-2637.

[6] BOCHAROVA I E,HUG F, JOHANNESSON R,,et al.Searching for voltage graph-based LDPC tailbiting codes with large girth[J].IEEE Transactions on Information Theory, 2012, 58(4): 2265-2279.

[7] KIM K J,CHUNG J H,YANG K.Bounds on the size of parity check matrices for quasi-cyclic low-density parity-check codes[J].IEEE Transactions on Information Theory, 2013,59(11): 7288-7298

[8] LAN L, ZENG L Q, TAI Y Y,et al.Construction of quasi-cyclic LDPC codes for AWGN and binary erasure channels: a finite field approach[J].IEEE Transactions on Information Theory, 2007, 53(7):2429-2458

[9] ESMAEILI M，JAVEDANKHERAD M.4-Cycle Free LDPC Codes Based on Difference Sets[J].IEEE Transactions on Communications, 2012, 60(12): 3579-3586.

[10] CHEN Chao，BAI Baoming，LI Zhuo, et al.Nonbinary Cyclic LDPC Codes Derived from Idempotents and Modular Golomb Rulers[J].IEEE Transactions on Communications,2012, 60(3):661-668.

[11] ZHANG Guohua,SUN Rong,WANG Xinmei.Several Explicit Constructions for (3,L) QC-LDPC Codes with Girth at Least Eight[J]. IEEE Communications Letters, 2013, 17(9): 1822-1825.

[12] GPS Navstar Joint Program Office. Draft IS-GPS-800，Navstar GPS space segment/user segment L1C interfaces[S]. California: GPSW Press, 2008.

(编辑：王敏琦)

s：The National Natural Science Foundation of China(61472464)；The Project supported by the Research Foundation of Education Bureau of Hunan Province,China(16C0686)；The Key discipline construction project funding for Hunan University of Science and Engineering(Electrical systems)

A new construction method of quasi-cyclic low-density parity-check codes with extending approximate lower triangular structure-quasi cyclic-low density parity check(eALT-QC-LDPC), based on modular Golomb rulers, was proposed. The new construction method can eliminate the short cycles of the girth-4, girth-6 and girth-8 without a computer search, the different codes with flexible code-lengths and code-rates can be constructed by setting the different parameters. The proposed construction method can assure that the error-correction performances of the codes are greatly improved under the premise of the linear encoding complexity. Simulation results show that all the error-correction performances of eALT-QC(5 913,3 952) code with the code-rate of 0.66, the eALT-QC(3 648,2 289) code with the code-rate of 0.63, the eALT-QC(1116,558) code and eALT-QC(684,349) code with the code-rate of 0.5, compared with those of the PEG code with the same code-rate, code-length and degree distribution as well as the QC-LDPC code with the same code-rate, code-length and the girth-8, are improved to some extent respectively. The bit error rate(BER) performance of eALT-QC-LDPC code with the code-rate of 0.5 is closer to that of the random LDPC code in IS-GPS-800 protocol, but the new eALT-QC-LDPC code is easier to be implemented and its storage space was reduced to a great extent. Therefore, the new construction method can play an important role in the channel coding scheme for navigation systems.

quasi cyclic-low density parity check(QC-LDPC) code; modular Golomb rulers; error-correction performance; bit error rate(BER)

2017-01-08

2017-05-22 通讯作者：李玲香 lilingxiang2013@hotmail.com

国家自然科学基金(61472464)；湖南省教育厅科技研究项目(16C0686)；湖南科技学院重点学科建设项目(电路与系统)

10.3979/j.issn.1673-825X.2017.04.007

TN911.22

1673-825X(2017)04-0468-06

New construction method of the eALT-QC-LDPC codebased on the modular Golomb rulers

(1.School of Electronics and Information Engineering ,Hunan University of Science and Engineering, Yongzhou 425199, P. R.China;2.Shool of Communication and Information Engineering, Chongqing University of Posts and Telecommunications,Chongqing 400065, P. R.China;3.School of Electronics and Information Engineering ,Hunan University of Science and Engineering , Yongzhou 425199, P. R.China;)