薄壁球壳真空吸附装夹变形力学分析与控制

何泽地，田东宁，杨金川，姚智慧

(1.中国工程物理研究院 材料研究所, 四川 绵阳 621700; 2.哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨 150001)

薄壁球壳真空吸附装夹变形力学分析与控制

何泽地1，田东宁1，杨金川1，姚智慧2

(1.中国工程物理研究院 材料研究所, 四川 绵阳 621700; 2.哈尔滨工业大学 机电工程学院, 黑龙江 哈尔滨 150001)

针对标准铝合金薄壁球壳零件的装夹变形问题，建立球壳变形的数学理论模型以及有限元仿真模型，实现了薄壁球壳真空吸附装夹状态的理论分析与仿真优化。明确了真空负压与装夹位置对球壳变形的影响；基于球壳与吸具之间的装夹位置关系，完成了吸具主要尺寸参数的优化设计。优化后吸具样件的测量结果表明，通过控制真空负压以及改变装夹接触位置，可以有效减小球壳的装夹变形，进而提高其加工的尺寸精度。

机械制造工艺与设备； 薄壁球壳； 真空吸附； 装夹变形； 有限元仿真

0 引言

薄壁球壳件特别是轻材料结构件，因其结构相对复杂、相对刚度较低和壁厚较小等特点，加工中需要使用特殊的工装进行装夹固定。而在实际加工中，不同的装夹方式甚至装夹过程会使薄壁球壳在加工前已经产生不同程度的变形，并影响装夹约束状态和加工模态。由此，薄壁球壳在机床上的装夹状态及其产生的整体或局部变形会影响工件的加工精度，也造成了不同程度的加工误差[1-3]，从而影响炸药武器在聚心爆轰作用下的等压变形精度，并进一步影响炸药爆轰性能。

关于薄壁球壳等弱刚性零部件加工装夹的相关研究已有较多，各自针对的问题也不尽相同。其中，王运巧等[4]和刘胤等[5]以减小装夹过程的弹性变形为目标，基于商业虚拟软件开展了弱刚性结构件铣削加工的装夹物理模型研究。李双跃等[6]以及Menassa等[7]和Kashyap等[8]利用有限元虚拟建模技术实现了加工件装夹优化并选择最佳定位支撑位置，从而减小了装夹变形。张磊等[9]和Kaya[10]通过不同方法研究不同装夹方式和装夹布局，明确了装夹力以及装夹位置对复杂薄壁件的影响。虽然现阶段的研究成果较多，但针对薄壁半球壳的车削加工装夹研究较少，并多以传统机械夹紧力作为研究点。

当前基于机械装夹的薄壁件加工变形主要从材料、工艺和夹具等角度进行控制或优化，且研究对象多为薄壁平面件。对于薄壁球壳，由于其传统机械卡盘式夹具造成的宏观变形较大，在某些特殊生产过程中一般采用真空吸盘式工装对球壳类零部件进行装夹。真空吸盘式工装又分为弧面、锥面以及平面3种形式，在车削过程中弧面及平面贴合吸具的设计与加工成本太高，表面质量要求也较高，不适用批量式生产。

因此，有必要基于现行锥面吸具，针对薄壁球壳在车削加工中的夹紧力、装夹位置以及装夹变形等进行研究，结合材料力学与有限元仿真技术，给出锥面吸具的优化设计方法并进行效果对比。

1 薄壁球壳真空吸附力学状态

1.1 球壳受力分析

根据理论力学和材料力学分析，薄壁半球壳经过与真空锥面吸具贴合(即由球壳外表面和吸具的内锥面实现接触)会出现整体和局部形变。加工前，薄壁球壳与真空锥面吸具之间的吸附装夹示意图如图1所示。

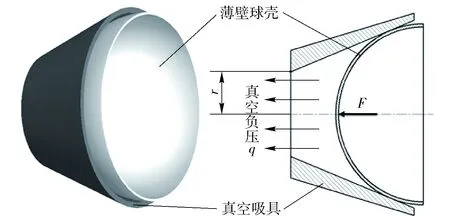
图1 真空吸附装夹示意图Fig.1 Clamping state during vacuum suction

图1中，q为真空负压，即吸附状态时的真空内外压强差。由图1可知，薄壁球壳与真空吸具装夹后，吸具内锥面与球壳外弧面形成圆周线接触，开启真空负压q后实现吸附装夹。由于吸具锥面对球壳形成了线支承并产生支承力，同时球壳内表面受到空气均布压强，产生等效作用力F，从而使球壳产生装夹变形。在考虑对称的情况下，球壳受力状态如图2所示。

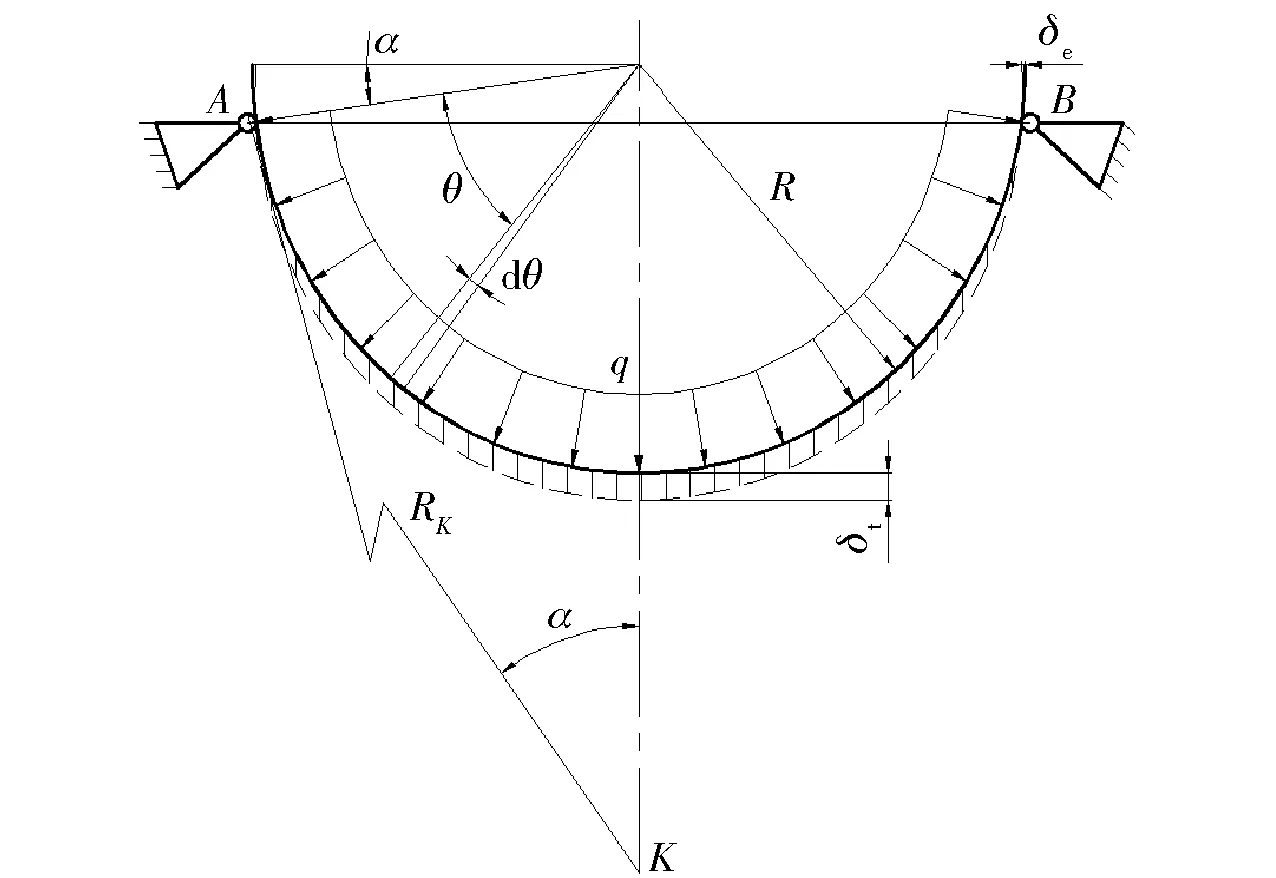
图2 球壳应变及其应力分布状态Fig.2 Strain and stress distribution states of spherical shell

图2中：α为吸具锥面角度与端面到支承点- 圆心连线之间的角度相等；R为球壳表面半径；θ为支承点- 圆心连线与计算点- 圆心连线之间的夹角；dθ为该微元段对应的弧度；δe为球壳端面变形量；δt为球壳顶部径向变形量；RK为锥面吸具的锥心位置距支撑点的距离，K为吸具锥面的虚拟锥心；A、B为任意截面处球壳的支撑点。

可将正圆弧形薄壁球壳件等效为薄壁缓倾斜球壳壳体[11]。根据材料力学中的薄壁壳体计算与理论[12]，球壳微元段径向受力状态关系为

dp=qRdθsin (α+θ)2πRcos(α+θ).

(1)

由(1)式可得出，球壳整体径向压力为

(2)

在空气压强作用并忽略球壳产生吸附滑移的情况下，球壳底部产生的径向挠度为装夹后的最大静态变形位置，其变形量计算的一般形式为

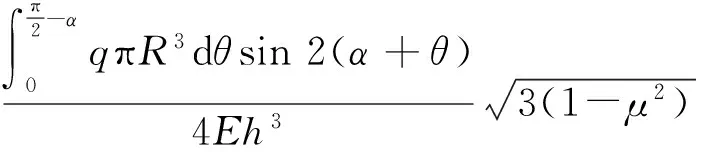
(3)

式中：E、h、μ分别为球壳材料的弹性模量、球壳壳体厚度、泊松比。

1.2 真空吸附力学模型

1.1节明确了薄壁球壳加工前的装夹静态力学状态，而在实际装夹过程中，还需要进一步考虑真空吸附和加工过程的可靠性与变形控制。

1)在吸具与工件形成的密封容积内，通过真空源抽出一定量的气体、产生真空负压q，进而吸具产生的等效吸附力[13]为

(4)

式中：k为真空有效吸附力系数，一般取值为0.9；C为换算系数，各参数单位为MPa、mm2、N时，取值为1；N为吸附时的安全系数，水平装夹时N≥4，垂直装夹时N≥8；S=nπr2k′为吸具的有效吸附作用面积，其中n为吸盘数量，r为吸具有效吸附半径，即吸具的最小真空管径，如图1所示，k′为吸取力方向的投影面积系数，根据图2所示几何关系，其值通过(5)式确定：

(5)

吸具有效吸附半径r=25 mm，为恒定值。

根据(5)式，在薄壁球壳采用水平装夹进行车削时，所需的真空吸附力为

(6)

根据(6)式，可得出在球壳重力和吸具结构确定的情况下，真空负压的设定范围为

(7)

由(7)式即可得出真空负压q的范围。在初设真空负压q时，F可等效为球壳重力G.

2)在进行车削时，为保证球壳能被吸紧, 在车削加工中不会转动滑移，必须使由球壳所受到的吸附力产生的与真空吸具之间的摩擦力Ff大于安全系数Q与切削力Ft的乘积，而摩擦力的大小与工件接触支承力Fn有直接关系，球壳所获得的支承力越大，则摩擦力越大。因此，球壳的切削力Ft与摩擦力Ff之间的关系为

Ff=ηFn≥QFt,

(8)

式中：η为铝合金与钢之间的摩擦系数，取值0.6；Fn为球壳总支承力，等效于工件接触支承力；Q为安全系数，取值为2.

根据图2和(2)式可得出，总支承力Fn与真空度之间的关系为

Fnsinα=p(θ).

(9)

已知6061铝的车削力大小为

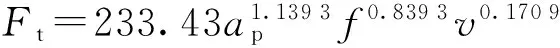
(10)

式中：ap为切削深度；f为进给量；v为切削速度。

将(2)式与(8)式、(9)式、(10)式联立，可得出真空负压q的预设下限值为

(11)

3)吸具内的真空负压q应在真空发生器最大真空负压的一定范围内选择，以提高真空吸着的能力，又不致使吸附的响应时间过长。而根据球壳加工过程中真空吸附系统的操作规程，真空负压应在真空发生器最大真空负压值的63%～95%范围内选择，即

q∈(0.63qmax，0.95qmax).

(12)

真空吸具在设计之初通常采用工件装夹后的夹紧误差，即装夹变形量来表征或评价吸具的设计参数[14]。因此，由(11)式、(12)式、(7)式与(3)式联立，并受到顶部变形量限值δl的控制，即可得出球壳真空吸附装夹变形的数学优化模型：

(13)

根据(13)式，吸具设计过程中的装夹变形优化变量为锥面角度α，考虑加工稳定性的优化变量为真空负压q.

通过(3)式、(6)式以及(9)式便可以表征薄壁球壳采用真空吸附装夹的力学状态，而(13)式则可作为优化真空锥面吸具及设定真空负压的基础理论与计算方法。

2 有限元仿真

根据薄壁球壳与真空吸具的装配关系，本文采用有限元软件ABAQUS来建立球壳真空吸附装夹的仿真模型。薄壁球壳材料为6061铝合金，其弹性模量及泊松比分别为E1=72 GPA和μ1=0.33；球壳尺寸为外径R=60 mm，厚度h=1 mm，球壳质量G=1.71 N.

真空吸具材料为45号钢，其弹性模量及泊松比分别为E2=210 GPA和μ2=0.3. 表面经过硬化处理，不考虑其锥面受力变形，可将其简化为刚体。

以支撑接触位置为界，整体有限元仿真模型在真空负压作用下受力矢量q的状态如图3所示。

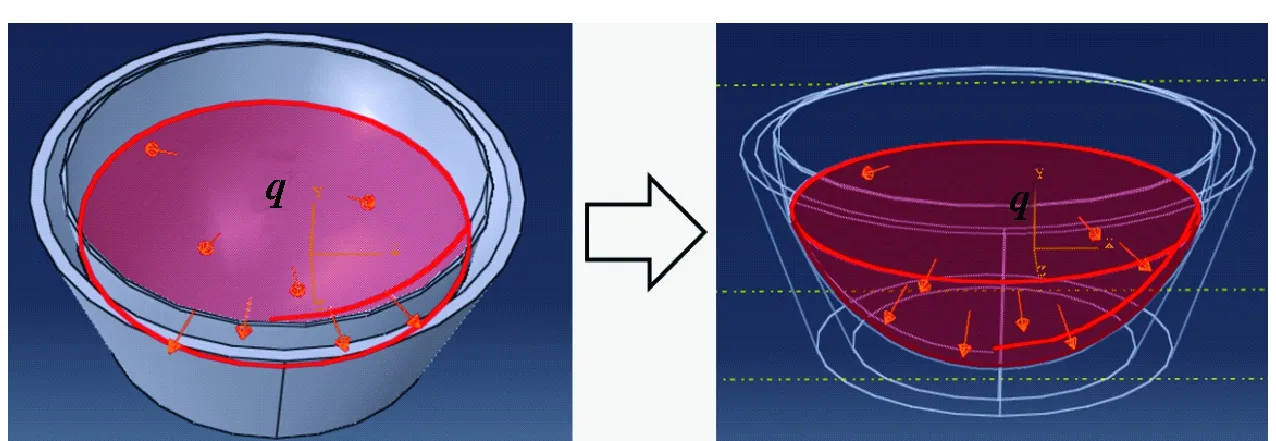
图3 装夹吸附受力状态的有限元模型Fig.3 Finite element model of suction

图3中，球壳与真空吸具分别采用C3D10(六面体)以及C3D8R(四面体)的三维应力实体单元。

2.1 仿真状态分析

在装夹过程中,由于装夹布局参数的不同,薄壁件的装夹变形程度也不同，装夹布局参数引起的工件装夹变形规律能够通过有限元方法获得[15]。

现将球壳的真空吸附接触位置以球壳弧面坐标表示，如图4所示。

图4 球壳吸附的不同接触位置Fig.4 Contact positions of suction

根据吸附状态下接触的位置不同，吸具的锥面角度也存在差异，各位置坐标状态如表1所示。

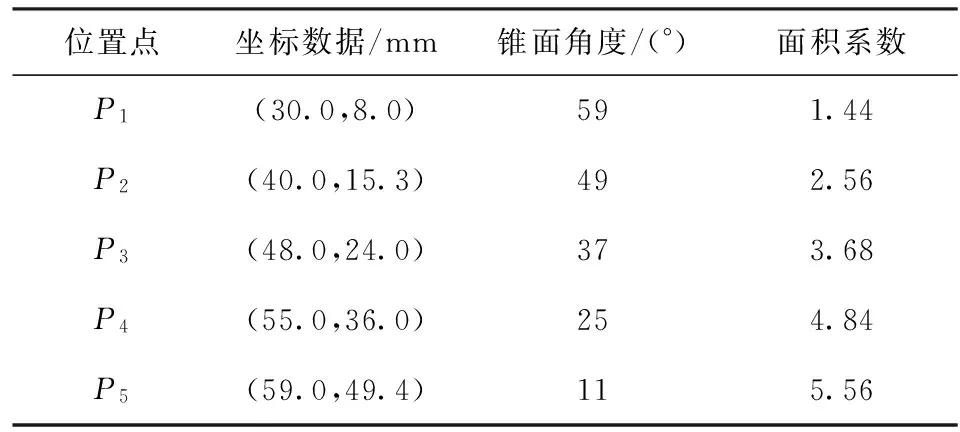
表1 吸附接触位置的坐标数据

根据表1所示吸具的锥面角度，分别针对球壳建立吸具的仿真模型。已知现阶段在球壳加工过程中设定的真空负压q=0.001 MPa. 5个不同吸附接触位置的仿真变形效果如图5所示。

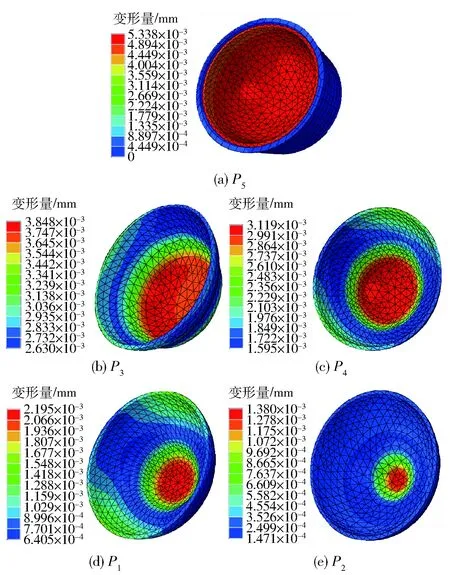
图5 不同接触状态下底部变形量Fig.5 Deformation of shell in different contact states during suction

将球壳尺寸、材料数据以及真空负压代入(3)式中，可得出在相同真空负压下，吸具锥面角度与球壳装夹变形量之间的关系，如图6所示。

图6 仿真后的变形趋势Fig.6 Deformation trend after simulation

由图6可知，装夹变形程度与吸具锥面角度之间呈反比，即吸具锥面角度越大，球壳变形量越小。

2.2 真空负压分析

图6中的变化趋势是在真空负压保持一致的情况下得出的。因此，根据(5)式，当吸附同一球壳时，根据吸附位置的不同，稳定吸附时所需的真空负压也存在差异。可以预知的是，锥面吸具角度越大，将球壳装夹固定在吸具上所需的真空负压最小值就越大，造成的球壳变形也就越大，从而对吸具系统提出了更高的要求。

根据(7)式理论模型、球壳状态数据以及相同仿真路径，可以得出在球壳不同吸附接触位置进行装夹时所需的最小真空负压，如图7所示。

图7 所需真空负压变化趋势图Fig.7 Changing curves of different vacuum negative pressures

由图7可知，锥面角度越大，所需最小吸附真空负压越小。当锥面角度α>37°时，所需最小真空负压已经明显大于当前真空负压限值(0.001 MPa)，在该真空负压作用下的球壳在P1点处的变形量如图8所示。

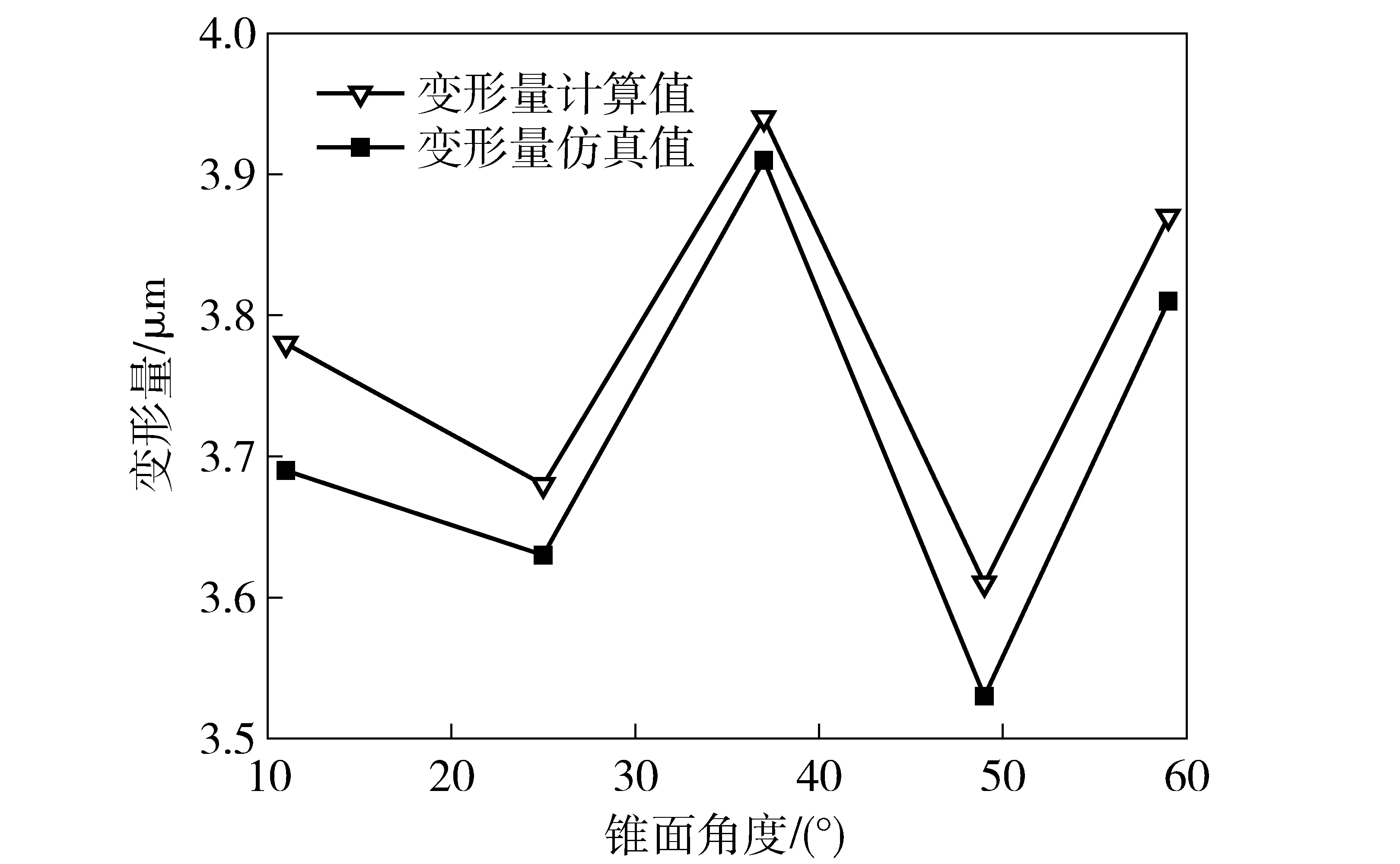
图8 所需最小真空负压状态下的球壳变形趋势Fig.8 Deformation trend of spherical shell under minimum vacuum negative pressure

结合图6并由图8可知，在设计真空吸具所需的最小真空负压作用下，当锥面角度α>37°时，相对于图6，对应球壳的装夹变形量增大了。

3 优化分析与设计

根据前文分析，球壳变形及其幅度大小与真空吸具的锥面角度α以及真空负压q有关。因此，根据(13)式可以对真空吸具进行优化设计。

优化前，需要明确设计输入条件如下：

1)待加工的薄壁球壳尺寸状态；

2)车削加工相关参数；

3)现有真空负压可用范围。

已知球壳材料为6061铝合金，球壳外径R=60 mm，厚度h=1 mm；铝合金与钢之间的摩擦系数η=0.6. 切削参数为：切削深度ap=0.3 mm；进给量f=0.1 min/r；切削速度v=100 m/min；真空吸附口半径r=25 mm；真空负压最大值qmax=0.001 0 MPa.

加工前，根据加工技术要求，球壳在真空吸附状态下产生的装夹变形量需控制在δl≤3 μm，则(13)式所建立的数学优化模型变形为

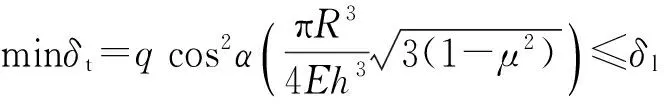
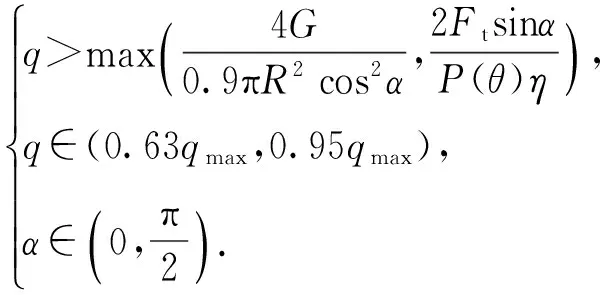
(14)

由(14)式得出的吸具锥面角度优化选择范围为

α∈(17.4°,29.6°).

(15)

将所属各参变量代入(14)式中，得出球壳真空吸附装夹的真空负压与锥面角度的优化结果为

(16)

根据上述优化结果，得出的吸附变形理论计算值为δt=2.31 μm，符合吸附装夹的变形控制要求。仿真结果和吸具样件(α=26.5°)如图9所示。

图9的仿真数据显示，吸附变形的仿真值为2.17 μm，吸附后所产生的装夹变形量减小了。

采用瑞典Serein公司产croma564改进型三坐标测量仪进行测量，其标准系统测量分辨率为0.05～0.07 μm，测量精度为0.5 μm. 此外，设计一个适用于工装与真空吸附系统的小型大理石平台，中间开孔以方便测量时的真空管路连接，先采用0.003 MPa进行球壳的初始固定，然后在精度为0.1 μm的端面激光位移传感器测量下进行装夹与端面对中，使其端面跳动控制在0.5 μm以下。

采用同平面垂直对称4点法，分别对经过优化后吸具样件和原36°锥面吸具装夹后的球壳内表面进行检测。分别在P1～P5所处的平面内(如图10中P1所处的同平面垂直4点P11～P14)检测，并与装夹前的球壳对应位置进行数据对比，采用测量点的内深变化量作为标定，从而得出装夹变形量。

经过检测后，原36°锥面吸具在0.007 5 MPa真空负压作用下，对比装夹前后的球壳测量数据，得出球壳的装夹变形量如表2所示。

经过检测后，优化后的吸具样件在0.007 5 MPa真空负压作用下，对比装夹前后的球壳测量数据，得出球壳的装夹变形量如表3所示。

由表2与表3的实际测量数据对比分析可知，优化后的吸具样件在球壳装夹后，球壳的变形量为1.60～2.80 μm，较原36°吸具的变形量大幅减小，整体变形控制效果明显。其中，25°位置由于接近球壳与吸具的接触点，其变形量最小；11°位置受到球壳整体变形影响，其变形程度较球壳底部小；球壳底部由于相对远离吸附支撑点，其变形也最大。

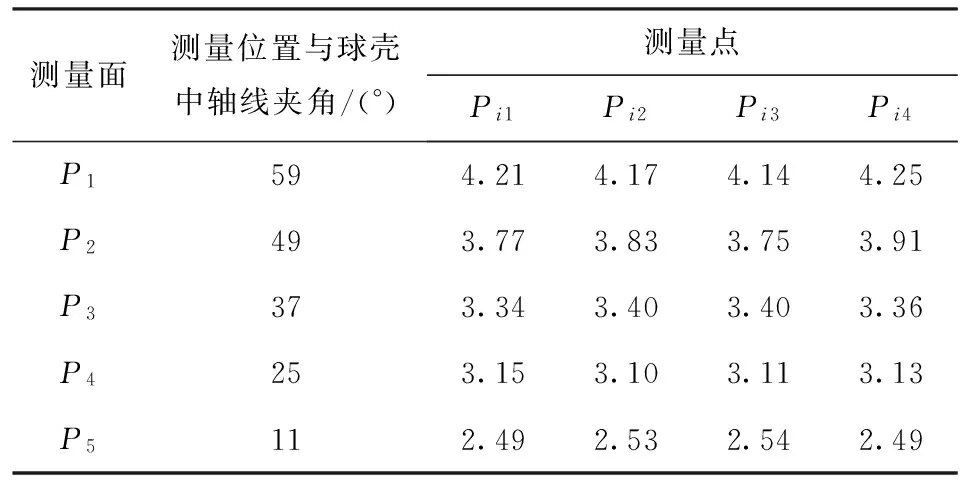
表2 原36°锥面吸具装夹前后的变形量

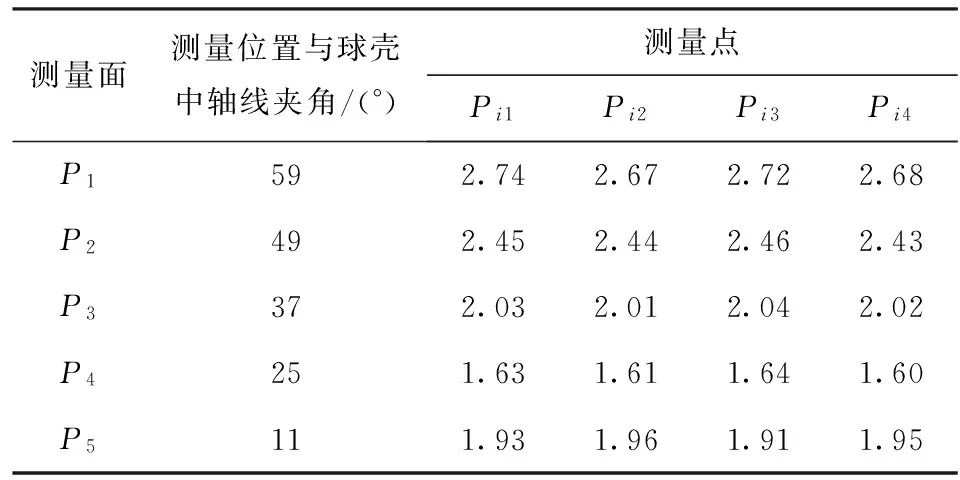
表3 26.5°锥面吸具装夹前后的变形量

综上所述，考虑到实际吸附装夹中存在一定的滑移以及测量误差，可以认为本文真空吸具的结构优化设计是合理有效的。

4 结论

通过理论分析和实例计算，得到如下结论：

1)吸具锥面角度与真空负压影响薄壁球壳真空吸附状态下的装夹变形。

2)基于该薄壁球壳真空吸附的力学状态等效数学模型及变形控制，可以较精确地得出吸具锥面角度的优化选择范围。

3)优化后的实例计算、仿真分析以及样件测量数据表明，通过优化真空负压及装夹接触位置，可以有效地减小薄壁半球壳产生的装夹变形，进而提高加工尺寸精度。

References)

[1] 秦国华，吴竹溪，张卫红．薄壁件的装夹变形机理分析与控制技术[J]. 机械工程学报，2007，43(4)：211-216． QIN Guo-hua,WU Zhu-xi,ZHANG Wei-hong. Analysis and control technique of fixturing deformation mechanism of thin walled workpiece[J]. Chinese Journal of Mechanical Engineering, 2007,43(4):211-216.(in Chinese)

[2] 王军，耿世民，张辽远，等．薄壁壳体件装夹变形机理有限元分析与控制[J]. 兵工学报，2011，32(8)：1008-1013． WANG Jun,GENG Shi-min,ZHANG Liao-yuan,et al. Finite element analysis and control of clamping deformation mechanism of thin-wall shell workpiece[J]. Acta Armamentarii, 2011, 32(8):1008-1013.(in Chinese)

[3] 李晖，张林林，常永乐，等．约束层阻尼对薄壁圆柱壳模态参数的影响研究[J].兵工学报，2016，37(7)：1338-1344. LI Hui, ZHANG Lin-lin, CHANG Yong-le, et al. The influence of constrained layer damping on modal parameters of thin cylindrical shell[J].Acta Armamentarii, 2016,37(7):1338-1344.(in Chinese)

[4] 王运巧，梅中义，范玉青．薄壁弧形件装夹布局有限元优化[J]. 机械工程学报，2005，41(6)：214-217． WANG Yun-qiao, MEI Zhong-yi, FAN Yu-qing. Finite element optimization of mechining fixture layout of thin-walled arc workpiece[J]. Chinese Journal of Mechanical Engineering,2005,41(6):214-217.(in Chinese)

[5] 刘胤，胡小秋．基于ABAQUS的弱刚度结构件装夹布局优化技术[J]. 工具技术，2008，42(11)：19-22． LIU Yin, HU Xiao-qiu. Optimum technology on clamping distribution of low-rigidity structure part based on ABAQUS[J]. Tool Engineering,2008,42(11):19-22. (in Chinese)

[6] 李双跃，刘建波．自动装夹设计中支承位置与工件变形的几何推理方法[J]. 组合机床与自动化加工技术，2003，58(8)：16-19． LI Shuang-yue,LIU Jian-bo. Geometric reasoning approach for supporting position and workpiece deformation in the automation fixturing design[J]. Modular Machine Tool & Automatic Manufacturing Technique,2003,58(8):16-19. (in Chinese)

[7] Menassa R J, Devries W R. Opimization methods applied to selecting support positions in fixture design[J].Journal of Manufacturing Science & Engineering,1991, 113(4):412-418.

[8] Kashyap S, Devries W R. Finite element analysis and optimization in fixture design[J]. Structual Optimization, 1999,18(2/3): 193-201.

[9] 张磊，陈克勤，张大顺，等．复杂薄壁件装夹变形控制研究[J]. 长春理工大学学报，2014，37(4)：89-92． ZHANG Lei,CHEN Ke-qin,ZHANG Da-shun,et al. Research on fixture deformation of the complex aluminum thin-walled parts[J].Journal of Changchun University of Science and Technology,2014,37(4):89-92.(in Chinese)

[10] Kaya N. Machining fixture locating and clamping position optimization using genetic algorithms[J]. Computers in Industry, 2006, 57(2):112-120.

[11] 章毅，陈力，李杰，等．薄壁壳在外部承受冲击荷载作用下的动力响应分析[J].工业建筑，2010，40(4)：46-50. ZHANG Yi,CHEN Li,LI Jie,et al.Analyses of the dynamic responses of the thin-walled shell under external impact[J]. Industrial Construction,2010,40(4):46-50.(in Chinese)

[12] 吉布森 J E．薄壳计算与理论[M]．北京：国防工业出版社，1989：101-109． Gibson J E. Thin shells computing and theory[M]. Beijing:National Defense Industry Press,1989:101-109.(in Chinese)

[13] 单景德．真空吸取器设计及应用技术[M].北京：国防工业出版社，2000：56-61． SHAN Jing-de. Design and application technology of vacuum absorption device[M]. Beijing:National Defense Industry Press,2000:56-61. (in Chinese)

[14] 蔡成，马术文，杨欣雨，等．装夹方案评价技术研究[J]. 机械设计与制造，2016，308(10)：207-029． CAI Cheng,MA Shu-wen,YANG Xin-yu,et al.Study on the evaluation technology of clamping scheme[J].Machinery Design & Manufacture,2016，308(10)：207-209.(in Chinese)

[15] 秦国华，赵旭亮，吴竹溪．基于神经网络与遗传算法的薄壁件多重装夹布局优化[J]. 机械工程学报，2015，51(1)：204-210． QIN Guo-hua,ZHAO Xu-liang,WU Zhu-xi.Optimization of multi-fixturing layout for thin-walled workpiece based on neural network and genetic algorithm[J]. Journal of Mechanical Engineering,2015，51(1)：204-210.(in Chinese)

Control and Mechanical Analysis of Clamping Deformation of Thin-walled Spherical Shell Workpiece during Vacuum Suction

HE Ze-di1， TIAN Dong-ning1， YANG Jin-chuan1， YAO Zhi-hui2

(1.Institute of Materials, China Academy of Engineering Physics, Mianyang 621700, Sichuan, China; 2.School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)

The thin-walled spherical shell workpiece is liable to deform during clamping before machining. A standard aluminum-alloy shell is taken for example. A mathematical model is established based on spherical deformation mechanism and finite element analysis. The theoretical analysis and simulation optimization are carried out for clamping design of semi-spherical shell with vacuum suction. The influences of suction strength and clamping location on deformation in the state of air pressure under average distributed load are analyzed. The result shows that the clamping deformation of shell can be minished effectively by controlling the suction strength and modifying the clamping location so that the machining size accuracy is improved. The main design parameter of vacuum fixture is optimized for the location relationship between shell and fixture.

manufaturing technology and equipment; thin-walled spherical shell; vacuum suction; clamping deformation; simulation

2016-11-27

装备“十二五”预先研究项目(42601070202)

何泽地(1963—), 男, 工程师。E-mail: hezedi@caep.cn

杨金川(1988—), 男,工程师。E-mail: yangjinchuan@caep.cn

TG751.1

A

1000-1093(2017)07-1409-07

10.3969/j.issn.1000-1093.2017.07.020