绕多孔孔板通气气体与液体两相横射流旋涡特性分析

刘涛涛， 王国玉， 张耐民， 黄彪

(1.北京理工大学 机械与车辆学院， 北京 100081；2.北京宇航系统工程研究所， 北京 100076)

绕多孔孔板通气气体与液体两相横射流旋涡特性分析

刘涛涛1， 王国玉1， 张耐民2， 黄彪1

(1.北京理工大学 机械与车辆学院， 北京 100081；2.北京宇航系统工程研究所， 北京 100076)

为了研究通气气体与液体两相流旋涡特性，采用RNGk-ε湍流模型并结合Level Set界面捕捉方法，对绕多孔孔板气体与液体两相横射流流动特性进行了数值模拟，并与实验结果进行了比较。研究结果表明：液相横流受到射流气体的阻碍作用在孔口上游、形成分离鞍点和马蹄涡，此分离鞍点随距壁面高度的增加逐渐靠近孔心，形成分离线；液相横流绕过射流气体后形成两个较为封闭的分离旋涡，此分离旋涡随距壁面高度的增加逐渐远离孔心。射流气体内部反旋转涡对的发展过程可分为3个特征阶段：流动位于孔口附近时，反旋转涡对从壁面逐渐形成，涡核间距和高度不断增大，影响面积不断扩张；随着流动向下游发展，反旋转涡对影响面积不断收缩直至消失；当流动发展至下游某一位置时，反旋转涡对在射流气体顶端再次形成，随着反旋转涡对的不断发展，在平板壁面诱导出2次涡对。

流体力学; 气体与液体两相流; 横射流; 数值模拟; 旋涡结构

0 引言

主动通气作为一种有效且易于实现的流场不稳定性调控措施，广泛应用于各类流体机械以及高速水下和水面航行体中。由于通气气体与液体(简称气液)两相流是一种复杂的多相湍流[1]，往往伴随着气、液之间的界面产生、运动等复杂物理过程，将产生复杂的涡旋结构[2]。

针对通气空化产生的复杂涡旋结构，人们开展了诸多实验与数值计算研究。Semenenko[3]根据实验结果和理论研究指出涡环泄气是由流动分离引起的复杂旋涡结构产生的，空泡尾流区充满了泡沫状的水气混合物。Kunz等[4]采用数值模拟对轴对称航行体在一定攻角下的稳态和非稳态自然空化及不含相变的通气空泡进行了研究，对比分析了航行体表面张力、空泡形态和阻力，描述了宏观流场的旋涡结构。文献[5-7]对绕回转体通气空化进行了一系列实验研究，通过Time-Resolved 粒子图象测速(PIV) 技术对尾流区域的旋涡结构进行了分析。Mäkiharju等[8]通过X射线实验和数值模拟对平板通气局部空化进行了细致研究，分析了高雷诺数下通气空化特征，研究了通气空化中的傅汝德数、雷诺数和韦伯数的影响，通过对空泡尾部闭合区旋涡结构的观测，发现闭合区域上游的湍流边界层导致压力波动作用于空气- 水的交界面并使其发生分离。Ji等[9-10]提出了“三分量”空化模型来捕捉空泡的发展，研究发现不可凝结气体抑制了自然空化下回射流的推进引起的大尺度旋涡结构，并且随着通气速率的增加，自然空泡会较为显著地被抑制。Wang等[11]对绕回转体通气空化空泡脱落机制进行了实验与数值计算研究，发现通气和回射流会在空泡内部上游和下游分别形成一个主涡，同时在二者之间诱导出一个2次涡，认为2次涡的运动和能量是空泡发生断裂脱落的关键因素。于娴娴等[12]对回转体通气云状空化进行了研究，发现通气和回射流相互作用下形成的旋涡结构会造成通气云状空化发展过程中空泡的部分脱落。时素果等[13]对绕空化器通气空化流动进行了数值计算，指出滤波器模型(FBM)能更加准确地捕捉通气空泡的涡旋结构。段磊等[14]对绕回转体涡环泄气方式下通气空化非定常流动特性进行了研究，结果表明空泡闭合位置的高压与空泡区域的低压形成较大逆压梯度，使空泡区域出现流动分离，进而在空泡区域产生复杂的旋涡结构，此旋涡结构与主流相互作用、引起了空泡断裂。胡晓等[15]比较了大涡模拟(LES)和RNGk-ε湍流模型对通气空泡尾部气体泄漏方式和空泡外形的影响，发现LES的瞬态计算结果更符合通气空泡的特性。王复峰等[16]采用实验和数值模拟相结合的方法对绕带不同尺度空化器的通气空化流场进行了研究，发现大空化器后部流动分离明显，存在更加复杂的旋涡运动。刘涛涛等[17]应用一种分域湍流模型对绕回转体通气超空化流动进行了研究，指出基于密度修正的模型可以较好地体现前端空泡的可压缩性，FBM模型可以捕捉尾部的多尺度空泡涡团结构。

当引入的主动射流气体以一定的角度从孔状或有限缝槽结构等较小过流断面通入水中时，与外部水流体相互作用，呈现出横射流特性(JICF)。关于横射流研究目前已经取得了很多有价值的成果，主要集中在单相流体介质，对多相流则涉及较少。Margason[18]将横射流流场总结为3个主要特征，使其成为一个理论体系：1)流体从射流孔射出后，在横流的推动下射流向下偏转，同时横流从射流两侧绕过射流，在横流的剪切作用下，射流形成了一对反旋转涡对(CVP)，该旋转涡对主宰着射流孔附近的流动；2)由于受到射流的阻滞作用，横流在射流孔前端会形成分离点和马蹄涡，马蹄涡尺度远小于CVP；3)绕过射流后，横向主流会在射流孔下游形成非定常的尾迹，尾迹涡的强度是3种涡结构中最弱的。Fric等[19-20]在3涡结构模型的基础上参照自由射流的特征提出了4涡模型，将射流孔内部溢出的剪切层涡环作为第4个涡系。Andreopouos等[21]通过实验首次发现在下游某处CVP下方还存在一对转向与之相反的涡对，称之为2次涡对。对于2次涡对的起源目前还存在争议。Morton等[22]认为2次涡对应该为马蹄涡的分支，Yuan等[23]通过LES反驳了这一说法，他们将该涡命名为壁面尾迹涡结构。Hale等[24]通过流油实验和数值模拟研究了多孔射流附近的流动，认为2次涡对是由进入射流下方低压区的横流下洗造成的。Yao等[25]对3孔布置的横流中射流进行了直接数值模拟，其研究表明，当孔间距为1倍孔径时，中间射流孔的CVP尺度受到两侧射流的影响，CVP被明显抑制。Roger等[26]对并排孔进行了LES数值研究，发现相邻两孔间距是影响射流下游流场涡结构的重要参数，当间距较小时，两股射流的掺混得到增强，射流孔下游的CVP尺度增大。吴海玲等[27]对二维横向射流进行数值模拟，比较了标准k-ε模型、RNGk-ε模型、Realizablek-ε模型等不同湍流模型对射流流动与传热特性预报的准确性，发现RNGk-ε模型、Realizablek-ε模型对流场及壁面对流换热特性的预测优于标准k-ε模型。赵马杰等[28]采用LES方法研究了高雷诺数下的横侧射流，指出JICF进场迎风涡是由于射流出口上游剪切层Kelvin-Helmholtz不稳定性引起的。

为了进一步研究通气空化产生的复杂旋涡特性，本文利用ANSYS CFX商业软件，采用均质多相流模型和RNGk-ε湍流模型，并采用Level Set界面捕捉方法对绕多孔平板流场进行数值模拟，从横射流角度分析了流场的涡旋结构。

1 数值方法

1.1 基本控制方程

采用均质平衡流模型，则Farve平均的Navier-Stokes方程为

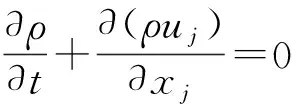
(1)

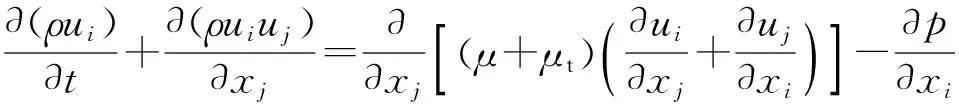
(2)

式中：ρ为流体密度；ui、uj为速度分量；p为压强；μ和μt分别为层流和湍流黏性系数。

1.2 湍流模型

标准k-ε模型是典型的雷诺时均化(RANS)湍流模型，它把涡黏系数和湍动能及湍动能耗散联系在一起，该模型由Launder等于1972年提出[29]，对于均相平衡流动的数值计算，标准k-ε模型的控制方程为

Pt-ρmε,

(3)

(4)

式中：Pt为湍动能生成项；ρm、μm分别为混合密度和混合湍流黏性；μt定义为

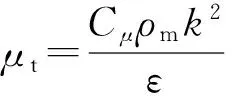
(5)

Cε1、Cε2、σε、σk、Cμ分别为模型常数。

RNGk-ε模型由Yakhot等[30]采用“重整化群”的数学方法推导得出，与标准k-ε模型的不同之处主要是在ε方程中增加了R项，即

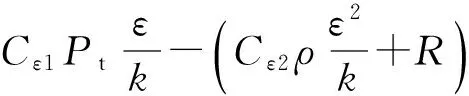
(6)

式中：R为流场变化度，定义为

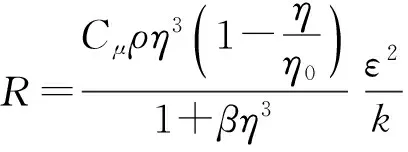
(7)

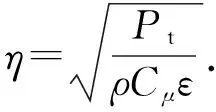
经化简得到RNGk-ε模型的ε方程为

(8)

相应的模型系数取值由理论分析得出，具体结果[31]列于表1中。在η<η0区域，RNGk-ε模型中的系数Cε1小于标准k-ε模型中的系数Cε1；在η>η0区域，RNGk-ε模型中的系数Cε1大于标准k-ε模型中的系数Cε1，因此与标准k-ε模型相比，在高应变率及流线弯曲程度较大的流场中，RNGk-ε模型将产生较小的湍流黏性系数。

表1 各湍流模型ε方程中Sε的表达式及模型常数

1.3LevelSet方法

在固定的欧拉坐标系中，含有相界面两相介质的流动可用Navier-Stokes方程[32-33]描述为

(9)

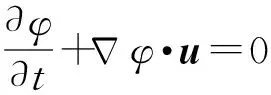
(10)

ρm(x)=ρa+(ρl-ρa)Hε(φ(x)),

(11)

μm(x)=μa+(μl-μa)Hε(φ(x))，

(12)

式中：ρa、μa分别为气相密度和气相湍流黏性；ρl、μl分别为液相密度和液相湍流黏性.

Level Set方法的主要思想是将界面定义为一个函数的零等值面(线)，即φ(x,t)=0. 令φ以适当的速度移动，使其零等值的面就是物质界面。

Level Set函数φ定义为

(13)

Heaviside函数Hε被定义为

Hε(d)=

(14)

式中：ε1是一个小量规整参数，恒为正。Heaviside函数也可以作为区分计算区域内介质种类的方法和指标。

借助于Level set函数φ，相界面的内在集合特性参数可被确定为

法向向量

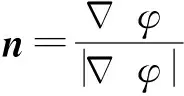
(15)

界面曲率

(16)

因而(9)式中的表面张力项可表示为

(17)

这样，(9)式就可以像求解单相流体的Navier-Stokes方程一样方便地求解了。

1.4 计算边界条件及设置

图1给出了平板几何参数，平板全长300 mm，宽70 mm，其表面设置4个通气孔，直径d=2.6 mm，间距(孔心之间距离)L=6.6d，位于距工作段前端60 mm处，工作段前后各有一段光滑过渡的导流段。图2为计算区域及边界设置条件。计算域总长3 500 mm，高度190 mm，边界条件设置为：速度入口，压力出口，速度、压力和含气率在流动方向的导数为常数，通气孔为质量流量入口，固壁为绝热、无滑移壁面条件。实验和数值计算中采用的来流速度v=5.1 m/s，通气体积流量系数Qs=m/(4ρavd2)=1.12，其中m为总通气质量流量(kg/s)，ρa为实验工况下气体密度(单位：kg/m3，实验工况pe=4 atm，Te=25 ℃). 数值计算中时间步长设定为0.000 5 s，总计算时间为0.1 s.

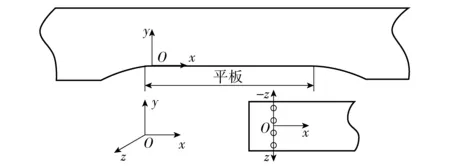
图1 计算模型几何参数Fig.1 Geometrical parameters of plate model

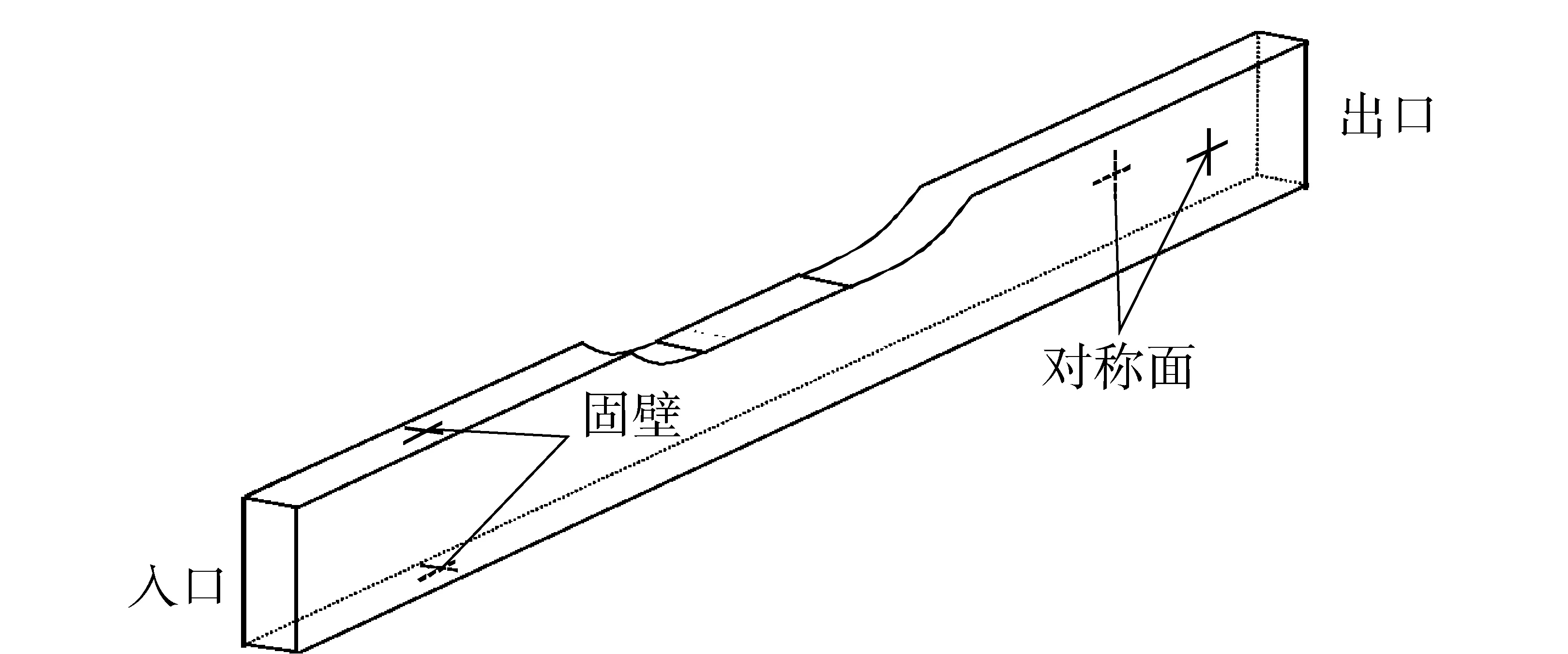
图2 计算区域及边界设置条件Fig.2 Computational domain and boundary conditions

图3给出了平板工作段及孔口附近的网格图。为了更准确地捕捉平板表面及孔口附近的旋涡结构，在近壁处及通气孔附近进行网格加密。近壁面y+值在30～150之间，满足壁面函数要求。

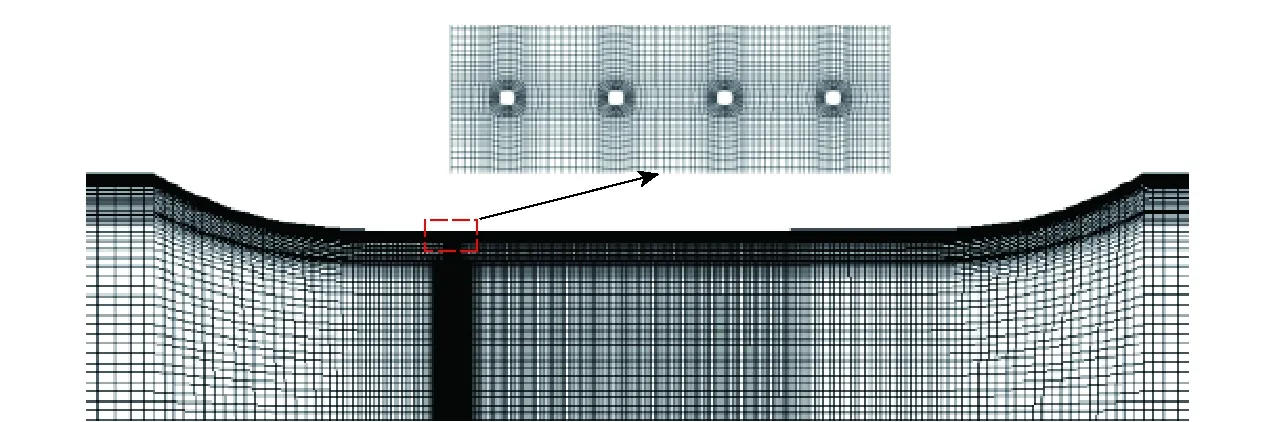
图3 平板工作段及孔口附近的网格图Fig.3 Computational grids around plate

分别取网格数为50万、100万、150万、180万和200万的网格进行网格无关性验证，其中为保证网格精度使计算准确，网格选择的标准为所有网格质量均在0.7以上，所得到的阻力系数分布如图4所示。

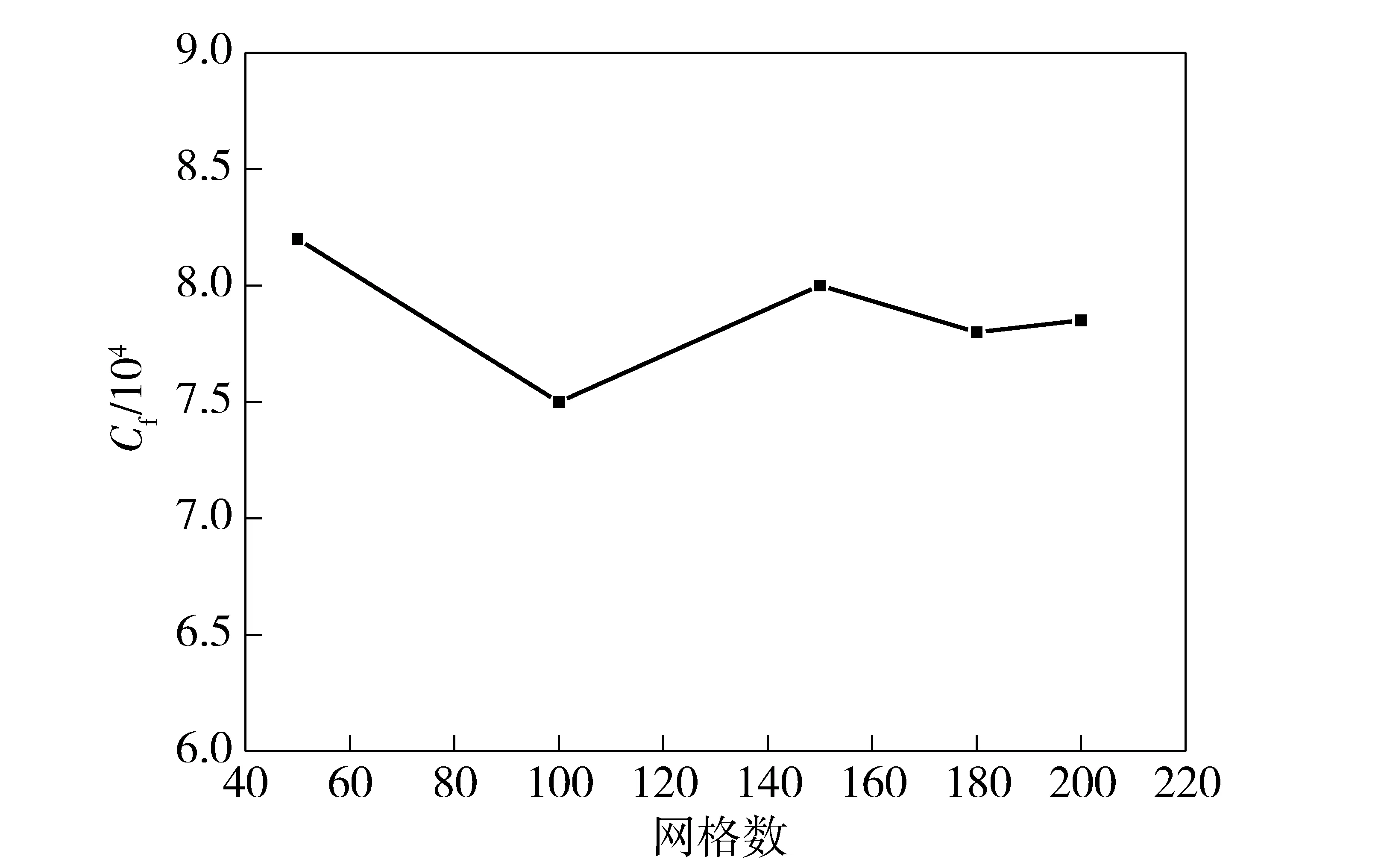
图4 网格无关性验证Fig.4 Verification of grid independence

由图4可知，当网格数达到150～200万时，可以发现所得到的阻力系数变化不大，因此在节省计算时间和保证计算结果精度的前提下，将网格数取为180万。

2 结果与讨论

2.1 数值与实验比较

图5给出了特定时刻数值模拟计算得到的空泡形态与实验结果的对比。从图5中可以看出，本文采用的数值模拟方法计算得到的空泡形态发展过程与实验结果具有较好的一致性，即空泡紧贴通气孔后部形成连续条状，随着流动向下游发展，空泡在通气孔后聚集并不断向周向膨胀、发生交汇，水气交界面清晰。由于实验中无法完全确保气体持续均匀通入，实验观测到的气泡非定常特性与数值计算存在较大差异。为了进一步说明数值计算方法的可行性，图6给出了实验观测的气泡外形与数值计算的对比，其中实验观测结果为多次结果的平均值，可以看出，数值计算得到的气泡外形与实验结果吻合较好。本文中采用的模型孔间距较大，各孔间流动发展规律基本一致，因此在接下来的分析中主要选取中心处单孔的流动特性进行分析。

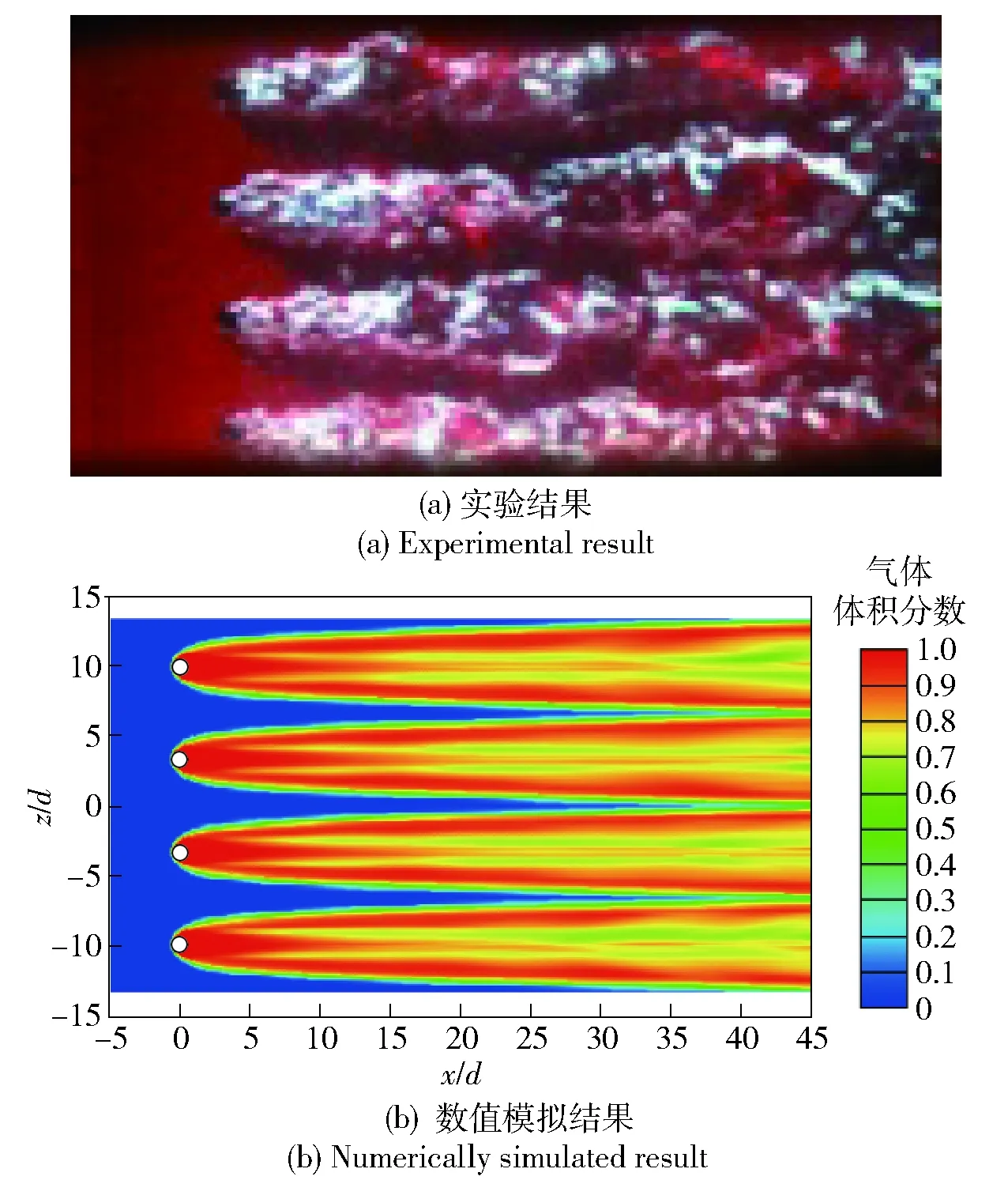
图5 实验与数值模拟得到的气泡形态对比Fig.5 Comparison of simulated and experimental cavity shapes

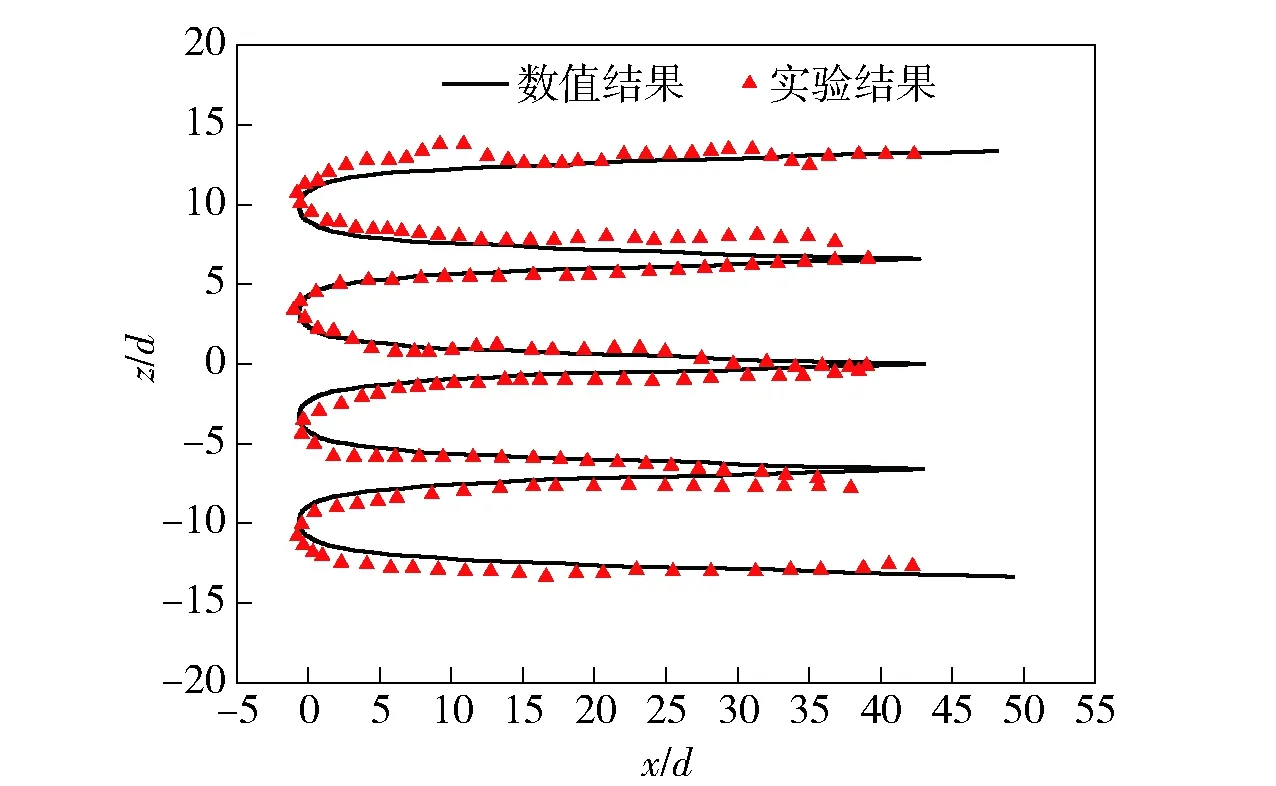
图6 实验与数值模拟得到的气泡外形对比Fig.6 Comparison of simulated and experimental cavity geometric shapes

2.2 孔口附近旋涡结构

图7和图8分别给出了孔口附近Oxy平面内涡量分布和相应的流线分布(以z/d=-3.3为圆心)。从图7和图8中可以看出，射流气体在液相横流作用下逐渐转变方向，由与横流正交变为与横流流动方向平行。由于受到射流的阻滞作用，横流在孔口上游x/d=0.583处形成分离鞍点和马蹄涡，此分离鞍点随距壁面高度的增加逐渐靠近孔心，形成分离线。横流绕过射流后，在孔口下游形成尾迹涡，此尾迹涡主要来源于壁面边界层。

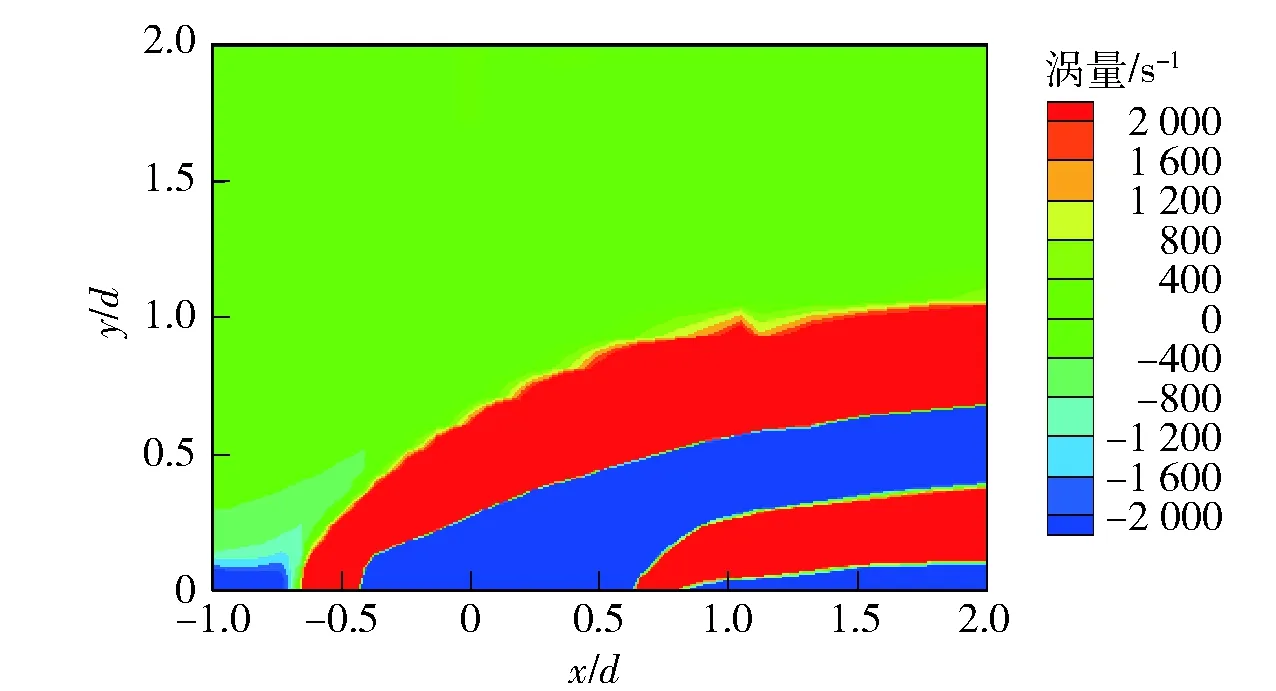
图7 Oxy平面涡量云图(z/d=-3.3)Fig.7 Contour of spanwise vorticity on vertical plane Oxy (z/d=-3.3)

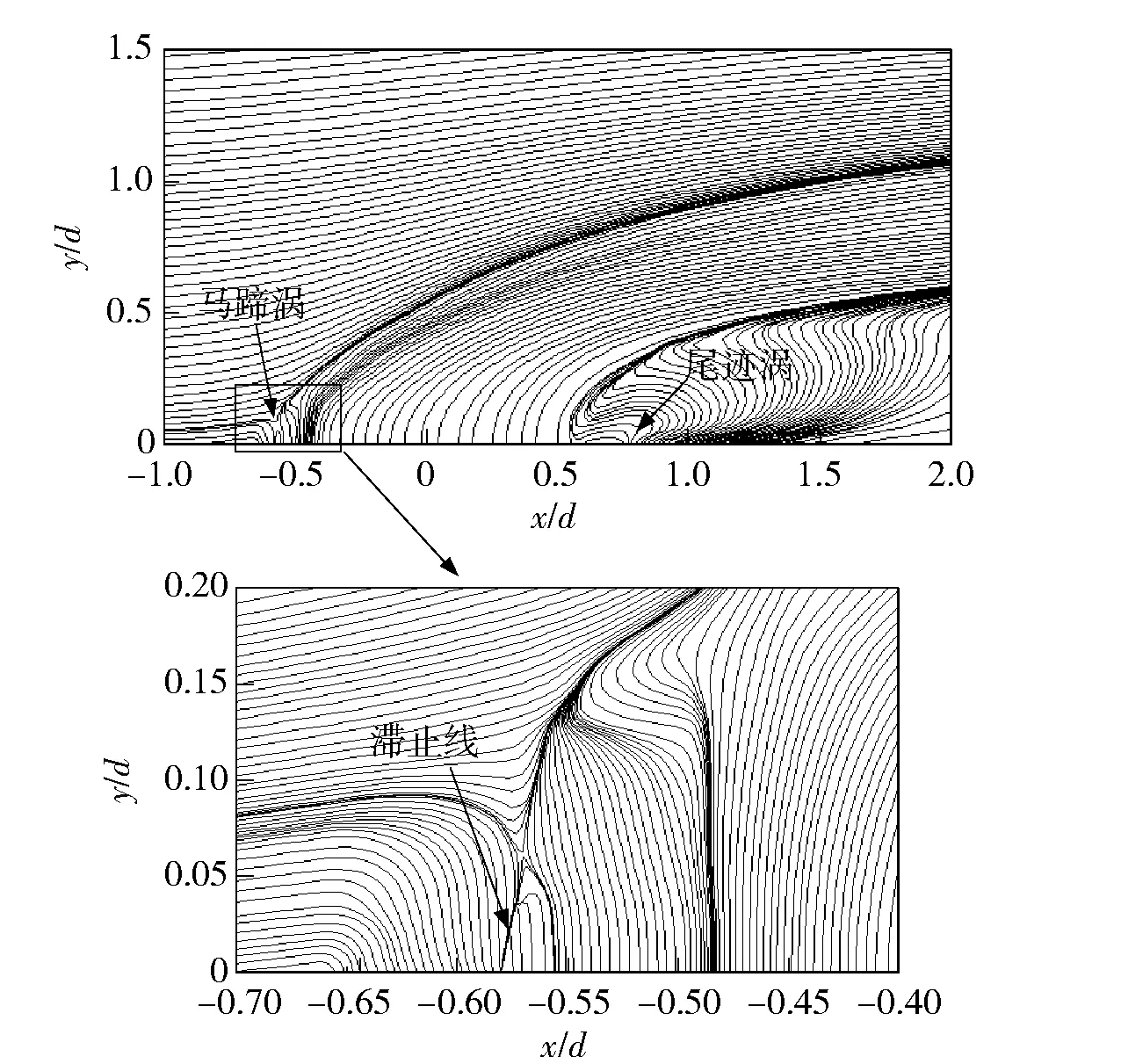
图8 Oxy平面流线分布(z/d=-3.3)Fig.8 Streamline patterns on vertical plane Oxy(z/d=-3.3)

为进一步分析孔口附近的旋涡结构，图9给出了距壁面不同高度Oxz平面内的流线分布(y/d=0，y/d=0.07，y/d=0.15，y/d=0.17)，其中蓝色线条为圆孔轮廓。由图9可以看出，当y/d<0.17时，流线均存在3个分离点、2个螺旋节点、1个临界节点和3条分离线。其中分离点S1位于孔口上游，与马蹄涡相关联，由其伸出的两条分离线L1和L2指出了马蹄涡的迹线，该分离线绕过气流后向外扩张发展，逐渐远离孔中心线。通气孔下游的分离点S3则对应于定常流动条件下刚性圆柱体绕流下游的滞止点，位于孔口下游，与该分离点直接连接的两个螺旋节点N2和N3，在孔口下游边沿形成两个分离旋涡，该分离旋涡主要由射流气体背面逆压梯度造成，这一现象与文献[34]中基本一致。分离点S2位于分离旋涡下游，横流绕过射流后于分离点S2处发生汇合并沿着流动的对称线向下游发展。图10给出了分离点S1、S2、S3以及分离旋涡涡核位置L随平板高度的变化趋势。结合图9和图10可以看出，随着y/d的增大，分离点S1逐渐靠近孔心，S2逐渐远离孔心，当y/d增大到0.17时，分离点S1消失，S2位置保持相对稳定。当y/d<0.06时，分离点S3与分离旋涡涡核位置基本重合，随着y/d的增大，分离点S3与分离旋涡涡核逐渐远离孔心，且两者间的距离逐渐增大，同时分离旋涡逐渐凸显，影响范围不断扩大。

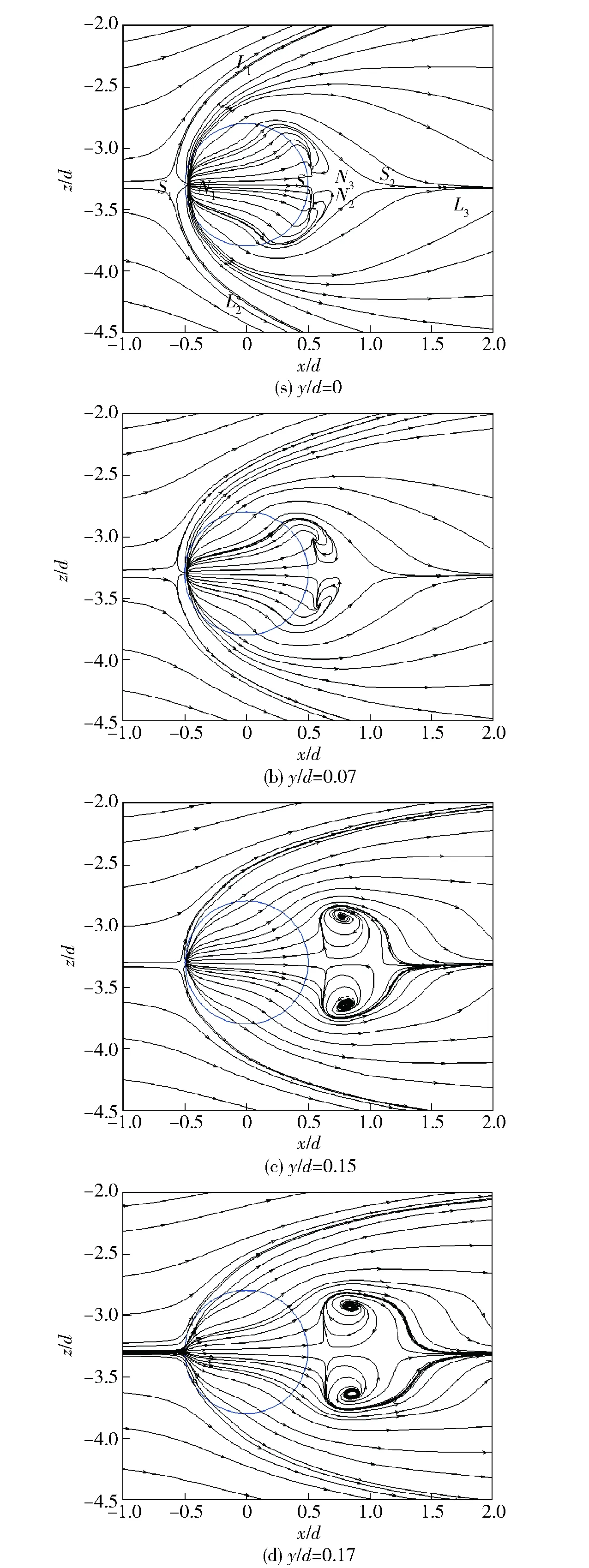
图9 Oxz平面流线分布Fig.9 Streamline patterns on a vertical plane Oxz

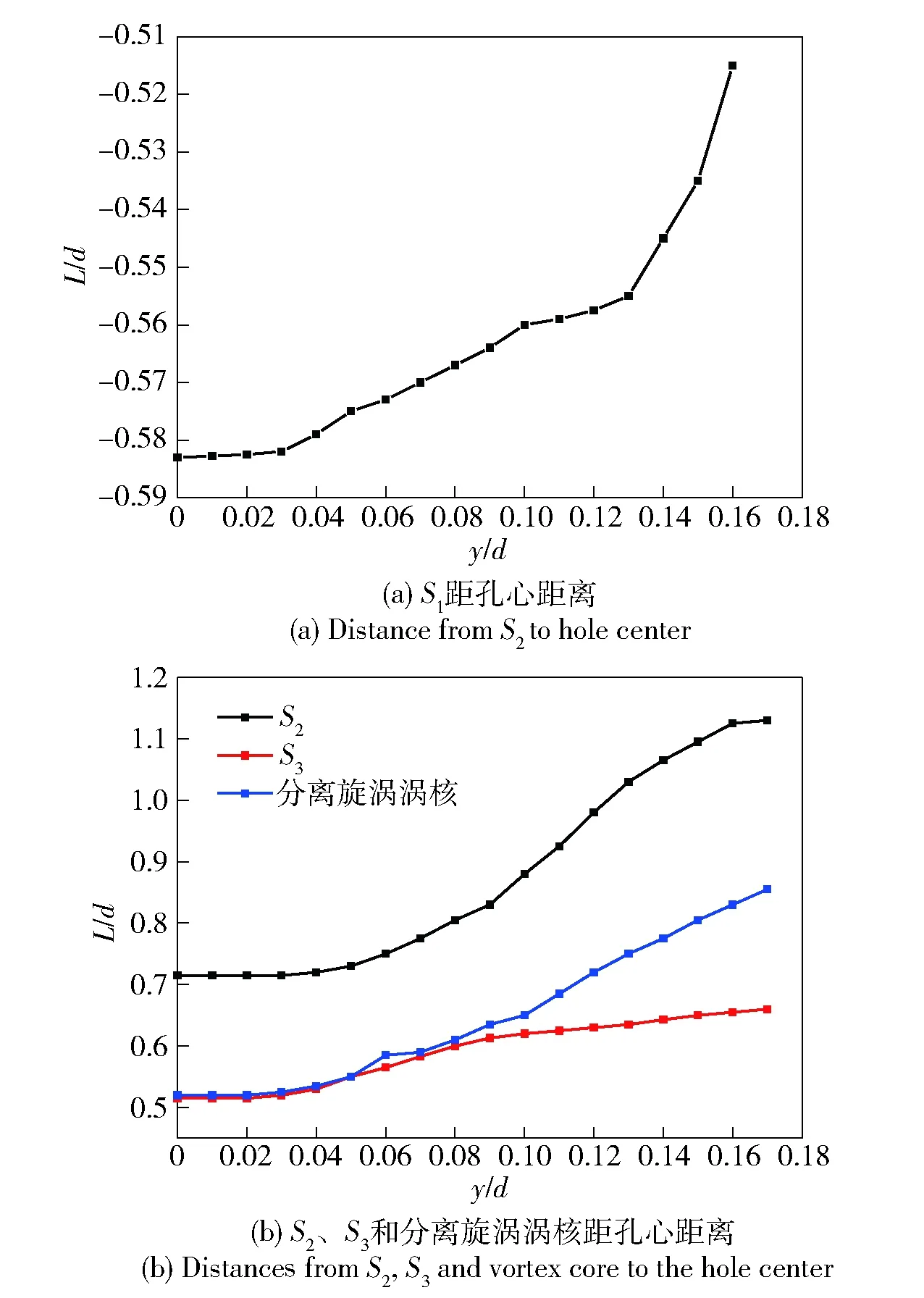
图10 滞止点和分离旋涡涡核偏移孔心距离与y/d的关系Fig.10 Relation among stagnation points, counter-rotating vortex cores and y/d

2.3 射流气体内部旋涡结构

为了进一步对射流气体内部的旋涡结构进行分析，图11给出了不同x/d位置处Oyz平面内流线分布和气相体积分数云图，可以看出在射流内部形成了以射流孔中心线为对称轴的一对涡量相等、旋转方向相反的涡对，即CVP. 图12给出了CVP涡核位置随流向距离的变化趋势，其中，横坐标表示沿流向距孔心的距离，纵坐标分别表示CVP涡核偏离孔中心线的距离E和距平板壁面高度H.

图11 不同流向截面位置流线分布Fig.11 Streamline patterns on different vertical planes Oyz

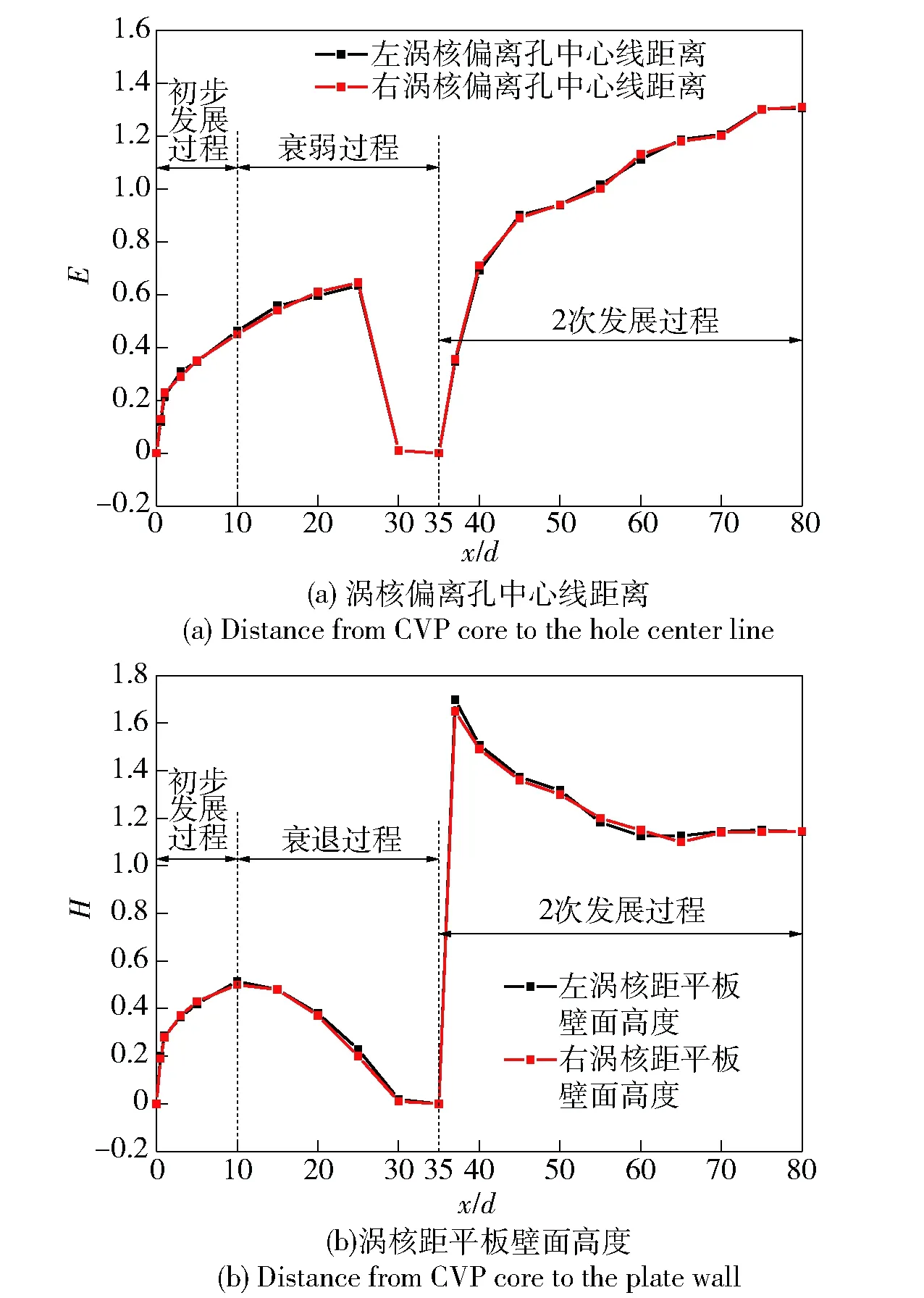
图12 CVP涡核位置随流向距离变化曲线Fig.12 Relation between CVP cores and x/d

结合图11和图12可以看出，CVP随流向的发展过程可以划分为以下3个特征阶段：

1)初步发展阶段(x/d=0～10)：当x/d=0时，CVP尚未形成，孔心处流线平行于y轴，随着向孔边界的移动，流线逐渐偏离y轴，趋于平行x轴，气体流线整体呈现发散状。随着流动向下游发展，在x/d=0.5处CVP开始形成，此位置与分离旋涡的分离点S3位置基本一致，说明CVP的形成可能与横流绕流分离旋涡有关。由于壁面的存在，此时尚未形成较为完整的涡对。当x/d=1时，射流气体内部已经形成较为完整的CVP，此阶段涡核偏离距离和高度呈现快速增长趋势。从x/d=1到x/d=5，由于黏性的作用，CVP流向断面的影响面积不断扩张，涡核偏离距离和高度呈现缓慢增长趋势。随着流动进一步向下游发展，CVP影响面积变化不显著，涡核偏离距离持续增大，涡核高度发展趋势逐渐趋于平缓，在x/d=10处达到峰值。

2)衰弱阶段(x/d=10～35)：这一阶段，CVP流向断面的影响面积不断收缩，涡核偏离距离持续增大，在x/d=25处达到最大，对应的涡核高度逐渐降低。当流动发展到x/d=30时，CVP基本消失，相应的涡核偏离距离和高度趋于0.

3)2次发展阶段(x/d=35～85)：这一阶段，CVP再次产生并不断发展，其影响面积远远大于初次CVP的影响面积。当x/d=36时，射流气体顶端流线发生扭曲，但仍未产生CVP. 随着流动向下游发展至x/d=37时，在射流气体内部再次形成较为完整的CVP，且影响面积较小。结合图11可以看出，刚形成的CVP位于射流气体顶端孔中心线附近，涡核间距较小，涡核高度较高，且左涡核高度要高于右涡核。从x/d=37到x/d=75，CVP影响面积不断扩张，涡核间距在x/d=45前呈现快速增长，跃过x/d=45后，涡核间距持续增大但增长速度减缓。涡核高度变化趋势与涡核间距变化趋势存在显著差异，在此阶段涡核高度持续下降至x/d=60，跃过x/d=60后，涡核高度保持相对平稳趋势。从图10(c)可以看出，在x/d=60处，CVP在平板壁面诱导出2次涡对，这一现象与Andreopoulos等[35]观测的实验现象基本一致。随着流动向下游发展，2次涡对被卷吸入CVP后消失， CVP影响范围扩大。在x/d=85位置处，2次涡对再次产生。由于2次涡对的周期性产生- 消失，使涡核相对保持在某一高度。

3 结论

本文基于均相流模型，采用RNGk-ε湍流模型并耦合对Level Set界面捕捉方法对绕多孔平板流场进行数值模拟，分析了通气气液两相横射流旋涡特性，主要结论如下：

1)液相横流受到射流气体的阻碍作用，在孔口上游形成分离鞍点和马蹄涡，此分离鞍点随距壁面高度的增加逐渐靠近孔心，形成分离线。

2)由于射流气体与液相横流相互作用，横流在射流背面出现绕流，形成两个较为封闭的分离旋涡，此分离旋涡随距壁面高度的增加逐渐远离孔心。

3)射流气体内部CVP的发展过程可分为3个特征阶段：初步发展阶段、衰弱阶段和2次发展阶段。流动位于孔口附近时，CVP从壁面逐渐形成，涡核间距和高度不断增大，影响面积不断扩张；随着流动向下游发展，CVP影响面积不断收缩直至消失；当流动发展至下游某一位置时，CVP在射流气体顶端再次形成，随着CVP的不断发展，在平板壁面诱导出2次涡对。

References)

[1] Brennen C E. Fundamentals of multiphase flow[M]. Cambridge, UK:Cambridge University Press, 2005.

[2] Cantro F, Crespo A, Manuel F, et al. Equlibrium of ventilated cavities in tip vortices[J]. Journal of Fluids Engineering, 1997, 119(4):759-767.

[3] Semenenko V N. Artificial supercavitation physics and calculation, ADP012080[R]. Kiev, Ukraine: Institute of Hydeomechanics of Ukrainian Academy of Science, 2001.

[4] Kunz R F, Boger D A, Chyczewski T S, et al. Multiphase CFD analysis of natural and ventilated cavitation about submerged bodies[C]∥3th ASME/JSME Joint Fluids Engineering Conference. San Francisco, CA, US: ASME, 1999.

[5] Wosnik M, Schauer T J, Arndt R E A. Experimental study of ventilated supercavitating vehicle[C]∥5th International Symposium on Cavitation. Osaka, Japan: Osaka University, 2003.

[6] Schauer T. An experimental study of a ventilated supercavity vehicle[D]. Minneapolis, MN, US: University of Minnesota, 2003.

[7] Wosnik M, Schauer T, Arndt R E A. Measurements in high void-fraction bubbly wakes created by ventilated supercavitation[J]. Journal of Fluids Engineering, 2013,135(1):531-538.

[8] Mäkiharju S A. The dynamics of ventilated partial cavities over a wide range of Reynolds numbers and quantitative 2D X-ray densitometry for multiphase flow[D]. MI, US: University of Michigan, 2012.

[9] Ji B, Luo X W, Zhang Y, et al. A three-component model suitable for natural and ventilated cavitation[J]. Chinese Physics Letter, 2010, 27(9): 38-43.

[10] Ji B, Luo X W, Peng X X, et al. Numerical investigation of the ventilated cavitating flow around an underwater vehicle based on a three-component cavitation model[J]. Journal of Hydrodynamics, 2010, 22(6): 753-759.

[11] Wang Y W, Huang C G, Wei Y P, et al. Ventilated partial cavitation shedding caused by the interaction of re-entry and air injection[C]∥Proceedings of the 8th International Symposium on Cavitation. Singapore: Nanyang Technological University, 2012.

[12] 于娴娴, 王一伟, 黄晨光, 等. 轴对称航行体通气云状空化非定常特征研究[J]. 船舶力学, 2014, 18(5): 499-506. YU Xian-xian, WANG Yi-wei, HUANG Chen-guang, et al. Unsteady characteristics of ventilated cloud cavity around symmetrical bodies[J]. Journal of Ship Mechanics, 2014, 18(5):499-506. (in Chinese)

[13] 时素果, 王国玉, 余志毅, 等. FBM湍流模型在非定常通气超空化流动计算中的评价与应用[J]. 船舶力学, 2012, 16(10):1100-1106. SHI Su-guo, WANG Guo-yu, YU Zhi-yi, et al. Evaluation of the filter based turbulence model for computation of unsteady ventilated supercavitating flows[J]. Journal of Ship Mechanics, 2012, 16(10):1100-1106. (in Chinese)

[14] 段磊, 王国玉, 付细能. 涡环泄气方式下通气空化的非定常流动特性研究[J]. 兵工学报, 2014, 35(5):712-718. DUAN Lei, WANG Guo-yu, FU Xi-neng. Research of the unsteady characteristics of ventilated cavitating flows in the form of gas leakage by toroidal vortex[J]. Acta Armamentarii, 2014, 35(5): 712-718. (in Chinese)

[15] 胡晓, 郜冶, 彭辉. 湍流模型对空泡形态影响的数值研究[J]. 计算力学学报, 2015，32(1): 129-135. HU Xiao, GAO Ye, PENG Hui. Numerical investigation on influence of turbulence model on cavity shape[J]. Chinese Journal of Computational Mechanics, 2015,32(1): 129-135. (in Chinese)

[16] 王复峰, 王国玉, 张敏弟, 等. 带空化器回转体空化流场研究[J]. 哈尔滨工程大学学报, 2015, 36(7):959-964. WANG Fu-feng, WANG Guo-yu, ZHANG Min-di, et al. Study of cavitating flows around an axisymmetric body with cavitators[J]. Journal of Harbin Engineering University, 2015, 36(7):959-964. (in Chinese)

[17] 刘涛涛, 王国玉, 段磊. 基于实验观测的分域湍流模型在通气超空化中的评价[J]. 北京理工大学学报, 2016, 36(3): 247-251. LIU Tao-tao, WANG Guo-yu, DUAN Lei. Assessment of a modified turbulence model based experiment results for ventilated supercavity[J]. Transactions of Beijing Institute of Technology, 2016, 36(3): 247-251. (in Chinese)

[18] Margason R J. Fifty years of jet in cross flow research[C]∥Proceedings of the AGARD Symposium on Computational & Experimental Assessment of Jets in Cross Flow. London, UK: Advisory Group for Aerospace Research and Development, 1993.

[19] Fric T F. Structure in the near field of the transverse jet[D]. Pasadena, CA, US: California Institute of Technology, 1990.

[20] Fric T F, Roshko A. Vortical structure in the wake of a transverse jet[J]. Journal of Fluid Mechanics, 1994, 279:1-47.

[21] Andreopoulos J, Rodi W. Experimental investigation of jets in a cross flow[J]. Journal of Fluid Mechanics, 1984, 138:93-127.

[22] Morton B R, Ibberson A. Jets deflected across flow[J]. Experimental Thermal and Fluid Science, 1996, 12(2):112-133.

[23] Yuan L L, Street R L, Ferziger J H. Large eddy simulation of a round jet in cross-flow[J]. Journal of Fluid Mechanics, 1999, 379:71-104.

[24] Hale C A, Plesniak M W, Ramadhyani S. Structural features and surface heat transfer associated with a row of short hole jets in cross flow[J]. International Journal of Heat and Fluid Flow, 2000, 21:542-553.

[25] Yao Y, Maidi M. Direct numerical simulation of single and multiple square jets in cross flow[J]. Journal of Fluids Engineering, 2011, 133(3):1201.

[26] Roger F, Gourara A, Most J M, et al. Numerical investigation on the reactive gas mixing through interaction between twin square jets side-by-side and a cross flow[J]. Journal of Chemical Engineering, 2004, 238:45-55.

[27] 吴海玲, 陈听宽, 罗毓珊. 应用不同紊流模型的二维横向射流传热数值模拟研究[J]. 西安交通大学学报, 2001, 35(9):903-907. WU Hai-ling, CHEN Ting-kuan, LUO Yu-shan. Numerical simulation of 2D jet to cross flow heat transfer with different turbulence models[J]. Journal of Xi’an Jiaotong University, 2001, 35(9):903-907. (in Chinese)

[28] 赵马杰, 曹长敏, 张宏达, 等. 高雷诺数湍流横侧射流的大涡模拟[J]. 推进技术, 2016, 37(5): 834-843. ZHAO Ma-jie, CAO Chang-min, ZHANG Hong-da, et al. Large eddy simulation of a high Reynolds number turbulent jet in cross flow[J]. Journal of Propulsion Technology,2016, 37(5): 834-843. (in Chinese)

[29] Launder B E, Spalding D B. The numerical computation of turbulent flows[J]. Computational Methods in Applied Mechanics and Engineering, 1974, 3(2): 269-289.

[30] Yakhot V, Orszag S A. Renormalization group analysis of turbulence[J]. Journal of Scientific Computing, 1986, 1(1): 3-5.

[31] Speziale C G, Thangam S. Analysis of RNG based turbulence model for separated flows[J]. Journal of Engineering Science, 1992, 30(10): 1379-1388.

[32] Huang B, Wang G Y, Zhang M D, et al. Level set model for simulation of cavitation flows[J]. Journal of Ship Mechanics, 2011, 15(3):207-216.

[33] 吴钦, 王国玉, 付细能, 等. 绕平板气液两相流数值计算方法[J]. 北京理工大学学报, 2014, 34(5):475-500. WU Qin, WANG Guo-yu, FU Xi-neng, et al. Numerical study on multiphase flows around a plane[J]. Transactions of Beijing Institute of Technology, 2014, 34(5):475-500. (in Chinese)

[34] Kelso R M, Lim T T, Perry A E. An experimental study of rounds jets in cross flow[J]. Journal of Fluid Mechanics, 1996, 306:111-144.

[35] Andreopoulos J, Rodi W. Experimental investigation of jets in a cross flow[J]. Experimental Thermal and Fluid Science, 1996, 12(2):112-133.

Analysis of Vortex Dynamics of Gas-liquid Two-phase Crossflows around a Porous Plate

LIU Tao-tao1, WANG Guo-yu1, ZHANG Nai-min2, HUANG Biao1

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.Beijing Institute of Astronautical System Engineering, Beijing 100076, China)

In order to investigate the vortex structures of multiphase flows around a porous plate, the flow characteristics of gas-liquid two-phase crossflows were numerically simulated by using the RNGk-εturbulence modeland the Level Set model. The simulated results are compared with the experimental results. The research results show that the separation point and the horseshoe vortex are formed since the crossflow is blocked by gas jet, which can be observed at the upstream of the jet hole. With the increases in the distance away from the wall, the separation point gradually gets close to the jet exit hole. The crossflow detours the jet and forms two counter-rotating vortices on the lateral edges of jet, and the vortex evolution depends upon the distance away from the wall. The counter-rotating vortex pairs (CVP) are formed in the jet region. The development process of the vortex pairs can be devided into 3 stages: in the near wake-region (i.e., close to the edge of the jet exit hole), the counter-rotating vortex pairs gradually form on the wall, and the increases in the heights of the vortex cores ae well as the distance between the cores lead to the expansion of vortex area. As the flow develops toward downstream, the area of CVP shrinks and even disappears entirely. Further downstream, the CVP appears again on the top of the jet corresponding to the formation of secondary vortex pairs in the near-wall region.

fluid mechanics; gas-liquid two-phase flow; crossflow jet; numerical simulation; vortex structure

2016-10-24

国家自然科学基金项目(51239005)

刘涛涛(1989—)，男，博士研究生。E-mail:liutaotao_0708@126.com

王国玉(1961—)，男，教授，博士生导师。E-mail: wangguoyu@bit.edu.cn

TV131.3+2

A

1000-1093(2017)07-1375-10

10.3969/j.issn.1000-1093.2017.07.016