基于线谱瞬时频率估计的被动声纳目标运动分析

李关防， 崔杰， 袁富宇

(江苏自动化研究所, 江苏 连云港 222061)

基于线谱瞬时频率估计的被动声纳目标运动分析

李关防， 崔杰， 袁富宇

(江苏自动化研究所, 江苏 连云港 222061)

针对被动声纳探测目标，提出了一种基于线谱瞬时频率估计的目标定位跟踪算法。该算法通过利用声纳探测目标的跟踪波束信息，建立高精度瞬时频率跟踪提取与多特征联合的目标定位跟踪模型，完成对目标高精度多普勒频移信息的实时提取。基于多特征观测方程，实现了对目标的定位与跟踪。仿真实验和海上试验结果表明：该算法可在观测平台不机动情况下，完成对目标的快速定位与跟踪；在相同平台机动条件下，相比传统纯方位算法，该算法的要素解算性能更加稳定，解算收敛时间缩短约4 min，进一步增强了工程适用性。

信息处理技术； 目标特征信息； 定位与跟踪； 运动特征提取； 被动定位

0 引言

舰艇目标被动定位跟踪问题是决定舰艇战斗力的关键技术之一，其性能的好坏直接影响着武器的打击效果，该技术吸引了国内外专家学者的广泛关注。传统目标定位跟踪算法仅利用声纳量测的目标方位信息，跟踪过程中观测平台必须进行至少一次有效机动，且解算收敛时间较长[1]。经过多年的研究改进，传统方法性能已接近理论的克拉美罗下限，性能难以大幅提升。同时，舰艇进行转向机动时，辐射噪声级显著提高，将影响舰艇的隐蔽性。

声纳波束域信息是指声纳经波束形成、目标检测与方位跟踪后，目标跟踪波束的输出信息，该信息中蕴含目标的固有振动、相对运动、螺旋桨叶片数及转速等特征[2]。本文采用“信息换时间/空间”的研究思路，充分挖掘提取声纳目标跟踪波束信息中的目标特征，用于目标定位跟踪，通过增加目标信息的维数，有望突破传统方法的局限性，是一个新的研究方向。

1 目标波束域信息特性分析

声纳经过空间波束形成后，实现了对多目标辐射噪声空间上的分离。目标跟踪波束输出信息是目标辐射噪声和海洋传播信道的综合反映，体现了目标辐射噪声的固有特性和战场态势的时空变换特性。被动声纳通过检测目标辐射的噪声来发现目标，并进行测向、测距。舰艇辐射噪声的平均功率谱中既有连续宽带谱，又有离散频率的线谱。这两种成分产生的机理不同，与深度的关系也不同。典型的目标辐射噪声功率谱形状如图1所示。

目标辐射噪声中的低频线谱在海中可实现远距离传播，当目标与观测平台存在相对运动时，目标线谱的瞬时频率将产生多普勒频移，其中携带着目标与接收平台的相对运动信息，可作为目标定位跟踪的重要信源。在利用目标跟踪波束信息中的线谱多普勒进行目标运动分析(TMA)方面，国内外学者进行了许多研究，体现在：Becker提出了方位- 频率TMA[3]，研究了方位- 多普勒频率TMA系统的可观测性问题。研究表明：当目标和观测平台都在同一个平面内作匀速直线运动时，通过利用方位和频率测量，目标的轨迹是可观测的，唯一的条件是目标方位变化率不为0[4]. 方位- 多普勒频率TMA系统较纯方位TMA系统具有更宽容的可测性条件、更快速的收敛性以及更高的参数估计精度[5]。近年来，国内相关研究院所一直跟踪国外的技术发展趋势，文献[6]研究了方位- 频率TMA系统的定位跟踪问题，分析了系统的可观测性，并建立了多种数学模型，但侧重于理论研究；王燕等[7]提出了一种基于浅海射线声学多途结构的单水听器水下TMA方法，该方法主要解决近距离TMA问题；刘圣松等[8]研究了一种水下静止平台对目标运动参数的联合估计方法，同样侧重于近距离目标，频率估计精度不高。综上所述可知，已有多数文献研究主要侧重于直接利用目标频率计算目标运动参数，但目标线谱的稳定跟踪是一直困扰算法应用的一个难题，限制了技术的推广应用。

2 波束域目标定位跟踪

针对舰艇对目标隐蔽、快速打击的需求，基于声纳波束域信息和目标方位，挖掘提取声纳波束域信息中的目标相对运动特征，经波束域信息预处理、目标运动特征跟踪提取与优化滤波、多维信息TMA及定位精度实时评估等步骤，能够解决观测平台不机动条件下，对匀速直线运动目标的定位跟踪问题，为舰艇快速使用武器提供支持。该技术的核心是目标运动特征跟踪提取和多特征联合的TMA，下面从线谱瞬时频率跟踪提取、多特征联合的目标定位跟踪两方面进行介绍。

2.1 线谱瞬时频率跟踪提取模型

线谱跟踪主要基于自适应Notch滤波器实现，该滤波器是一种中心频率可调的窄带滤波器，它具有固定参数滤波器所不具备的优点。工作原理如图2所示。

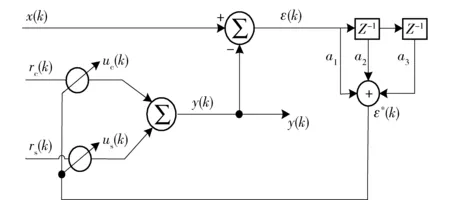
图2 Notch滤波器原理框图Fig.2 Functional block diagram of notch filter

假定输入信号x(k)=s(k)+n(k)，其中：s(k)为线谱信号，n(k)为噪声，参考角频率ω0=2πf0/fs，对应参考信号频率f0，ωd=ω-ω0为s(k)与参考信号的频率差异，fs为信号采样频率。正交参考信号分别为

rc(k)=cos(ω0k),

(1)

rs(k)=sin(ω0k).

(2)

自适应运算采用改进的最小均方算法，自适应学习迭代过程为

(3)

式中：uc(k)、us(k)为自适应陷波滤波器的权序列；u为自适应收敛因子；y(k)为自适应陷波滤波器的输出；a1、a2、a3为加权系数。设υ(k)为自适应陷波滤波器权序列构成复序列，具体表达为υ(k)=uc(k)-jus(k).

利用复序列υ(k)，实时计算线谱的瞬时频率与前一时刻频率fk的差值fd，估计线谱的瞬时频率fk+1，具体表达为

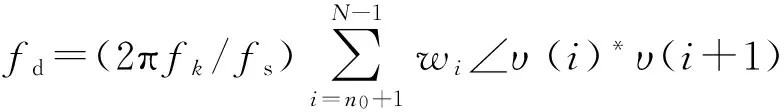
fk+1=fk+fd,

(4)

若当前为初始时刻，则通过上述过程确定线谱瞬时频率与初始参考频率的差值，将其与参考频率求和，获得线谱高精度的瞬时频率，并据此更新自适应陷波滤波器的参考频率，作为下一时刻的参考；若当前时刻非起始时刻，则以前一时刻瞬时频率为参考，利用自适应陷波滤波器的权值，确定线谱瞬时频率与参考频率的差值，获得线谱的瞬时频率。

仿真条件下，利用本文模型，线谱瞬时频率跟踪提取与误差曲线分别如图3和图4所示.

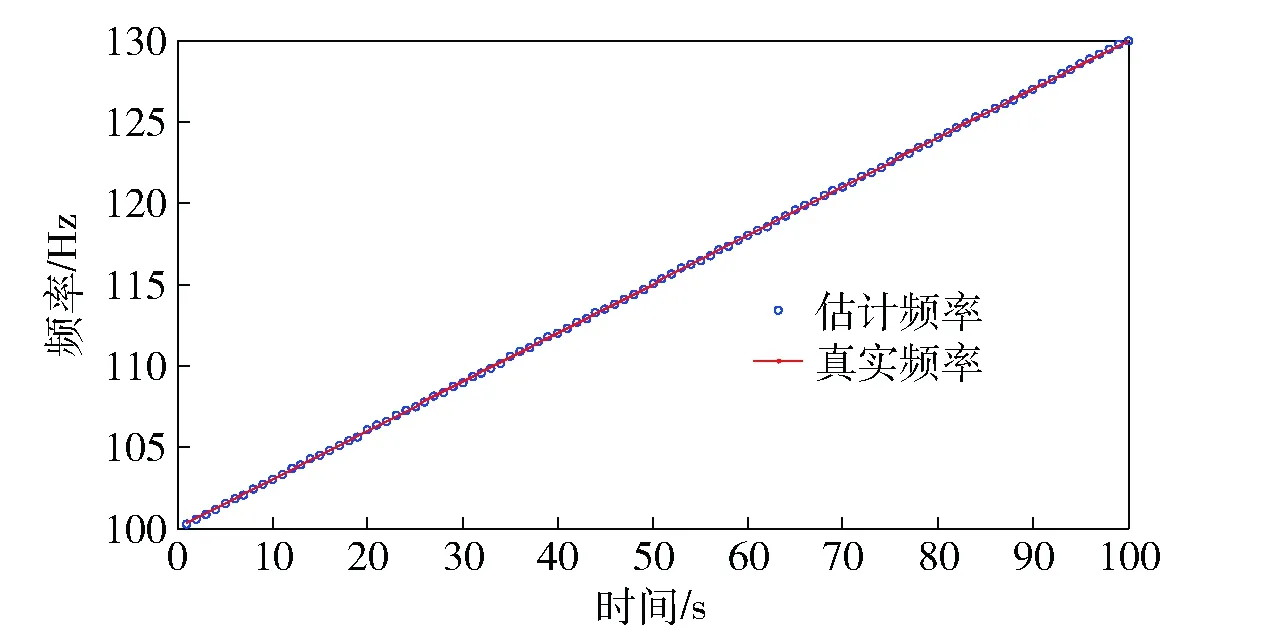
图3 线谱瞬时频率跟踪提取结果Fig.3 Extracted results of line spectrum instantaneous frequency

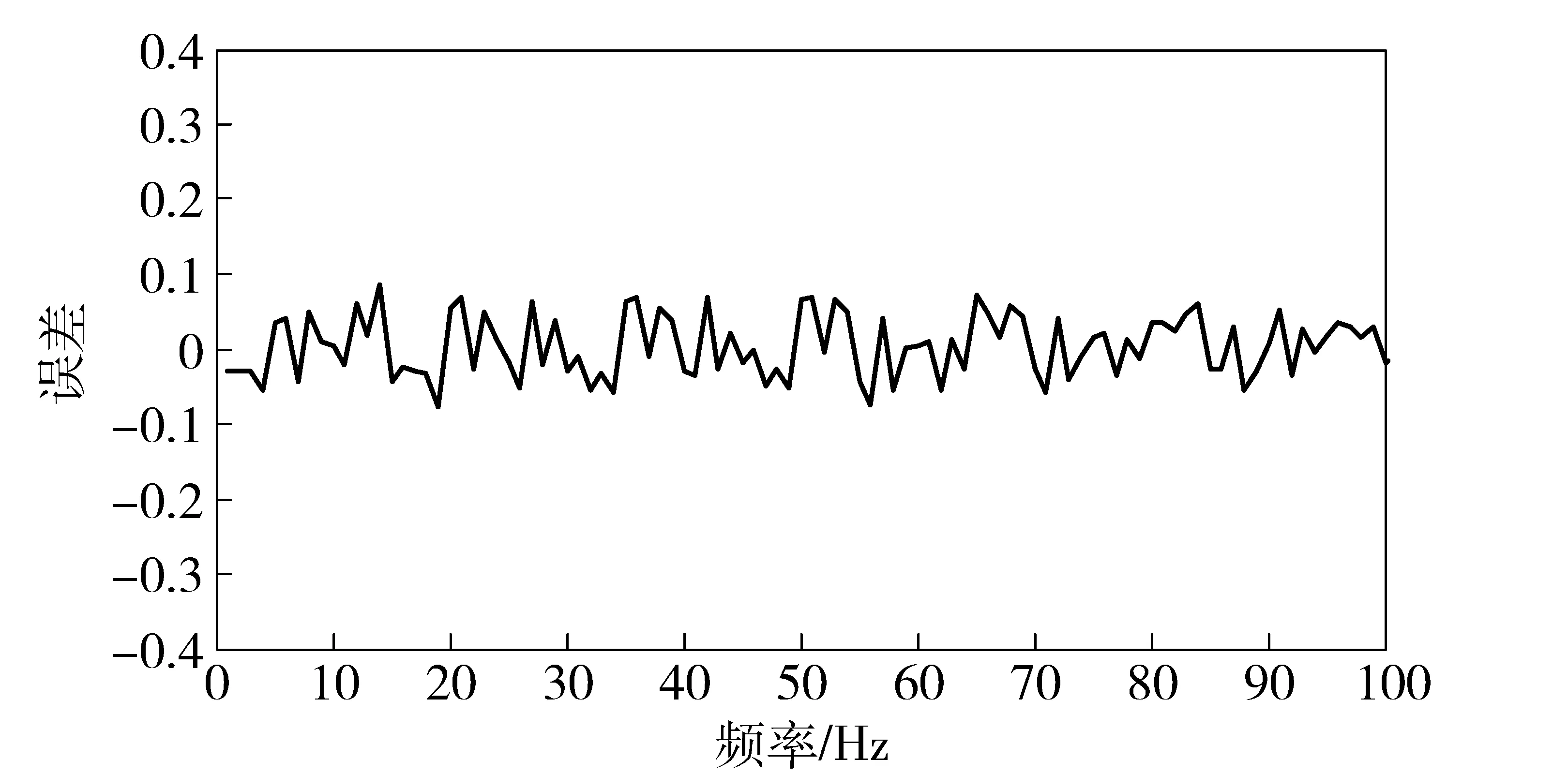
图4 线谱瞬时频率误差曲线Fig.4 Error curve of instantaneous frequency

为了深入验证该模型在真实海洋环境下的效果，利用该算法对海上采集的某船跟踪波束信号进行线谱跟踪提取，结果如图5所示。

图5 某船目标线谱瞬时频率自动跟踪提取结果Fig.5 Line spectrum instantaneous frequency tracked from a ship beam signal

仿真及试验数据处理结果表明：本文所述算法可以自动完成高精度线谱瞬时频率的跟踪提取，可为后续模型提供高质量的线谱瞬时频率信息。

2.2 多特征联合的目标定位跟踪模型

假设在观察时间内，目标沿固定的方向作匀速运动，目标辐射噪声中包含频率为f0的分量(具体数值未知，且可能存在多个)，则观测平台与目标不存在相对运动时，目标波束域信号中线谱频率将保持f0不变。敌我运动态势如图6所示，图中：Km为目标航向；vm为目标航速；Mk分别为k时刻的目标位置；Dk分别为k时刻目标距离；Bk分别为k时刻目标方位；vw(k)、Kw(k)为k时刻观测平台航速、航向。

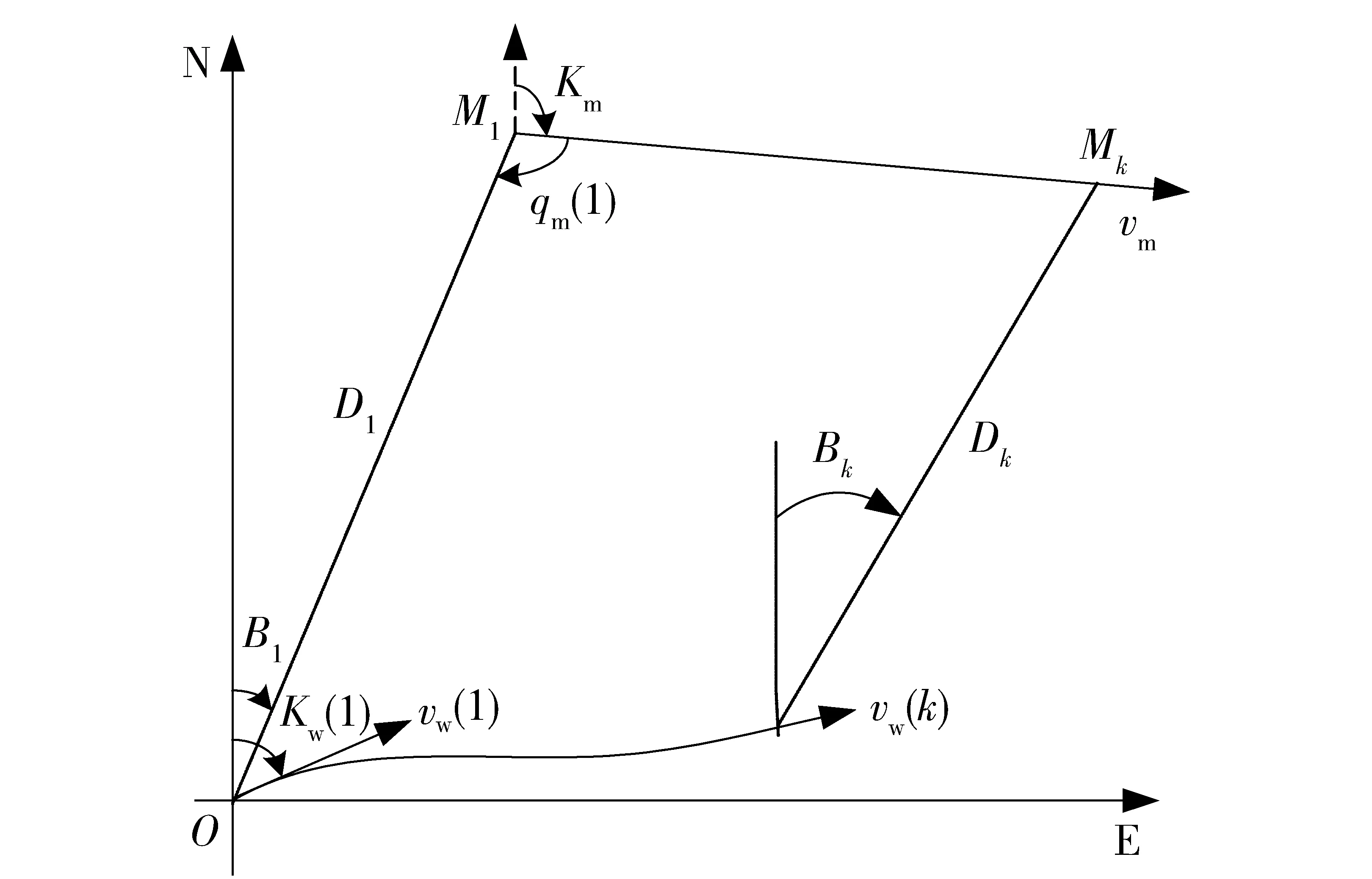
图6 敌我运动态势图Fig.6 Situation chart of observation platform and target movement

目标舷角qm是指目标航向线与目标、我舰连线的夹角，左负、右正，k时刻目标舷角qm(k)为

qm(k)=Bk-Km±180°.

(5)

若观测平台与目标存在径向运动，观测平台声纳目标跟踪波束信号中的线谱频率时发现存在多普勒频移，量测方程为

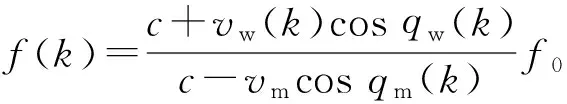
(6)

式中：c为海水中声速；qw(k)为k时刻我舷角；f0为目标辐射固定线谱频率；f(k)为k时刻估计频率；B为目标方位。对(6)式进行变换，可得：

f(c-vmcosqm)=f0(c+vwcosqw)

(vxsinB+vycosB)f-(c+vwcosqw)f0=-fc，

(7)

式中：vx、vy分别为我速度横向、纵向分量。

在直角坐标下，假设目标的运动状态向量X记为X=(x0,y0,vx,vy,f0)T，(x0，y0)为目标初始时刻坐标，则观测方程可表示为

k=1,2,3,….

(8)

由(8)式可以得到频率量测向量方程为

(9)

同样，根据方位量测，可以得到方位量测向量方程为

(10)

式中：(xwk,ywk)为k时刻观测平台的位置坐标。

联合频率量测向量方程、方位量测向量方程，利用最小二乘参数估计方法可解得：

X=(HTH)-1HTZ.

(11)

目标在观测时间内作匀速直线运动，该模型是可观测的。若波束域信息中含有多个线谱，可建立多线谱量测向量方程，使线谱根数增加，有助于提高算法对线谱频率误差的容忍度，增强算法的稳健性。

2.3 仿真验证与性能分析

下面进行仿真统计分析以验证算法的性能，仿真条件：目标匀速直线运动，目标方位误差采用高斯白噪声，误差不大于1°. 仿真统计时，根据目标初距的远、中、近，速度的高、中、低，初始舷角的大、中、小原则，进行航路选取。对每个航路进行1 000次蒙特卡洛仿真，统计每个航路的收敛时间和收敛率。对每个态势运行时间30 min，采样周期1 s，性能统计分析结果如表1所示。

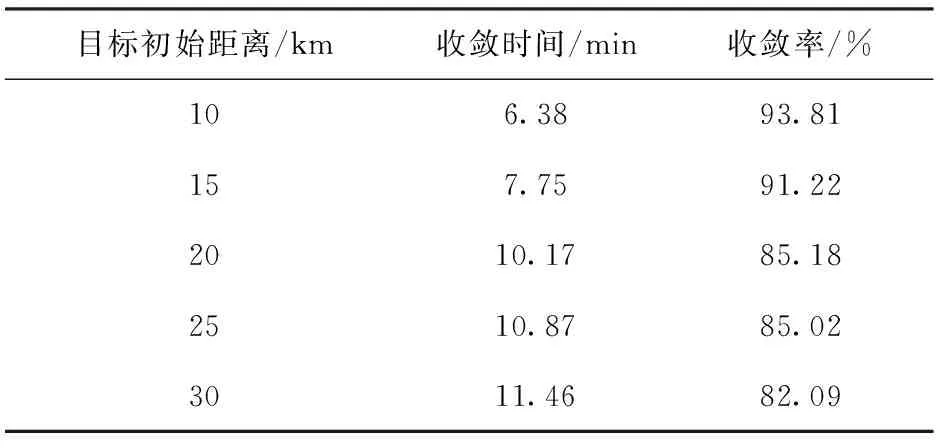
表1 不同目标初始距离条件下本文算法性能统计

仿真分析结果表明：1)本文所述算法可实现观测平台不机动条件下对目标的定位与跟踪；2)在不机动条件下，对于10～30 km的目标，本文算法的解算收敛时间约为6.38～11.46 min；3)随着目标距离的增加，解算收敛率略有降低，但均高于80%，具有良好的稳定性。

2.4 海上试验验证

为了进一步验证算法的实际效果，在海上实时采集声纳目标跟踪波束信息、目标方位及导航信息，进行模型验证。

2.4.1 海上试验航路1

本航路目标初始距离为54链(约10 km)、航速8 kn，观测平台匀速直线航行，航速、航向信息及目标谱特征提取结果如图7和图8所示。

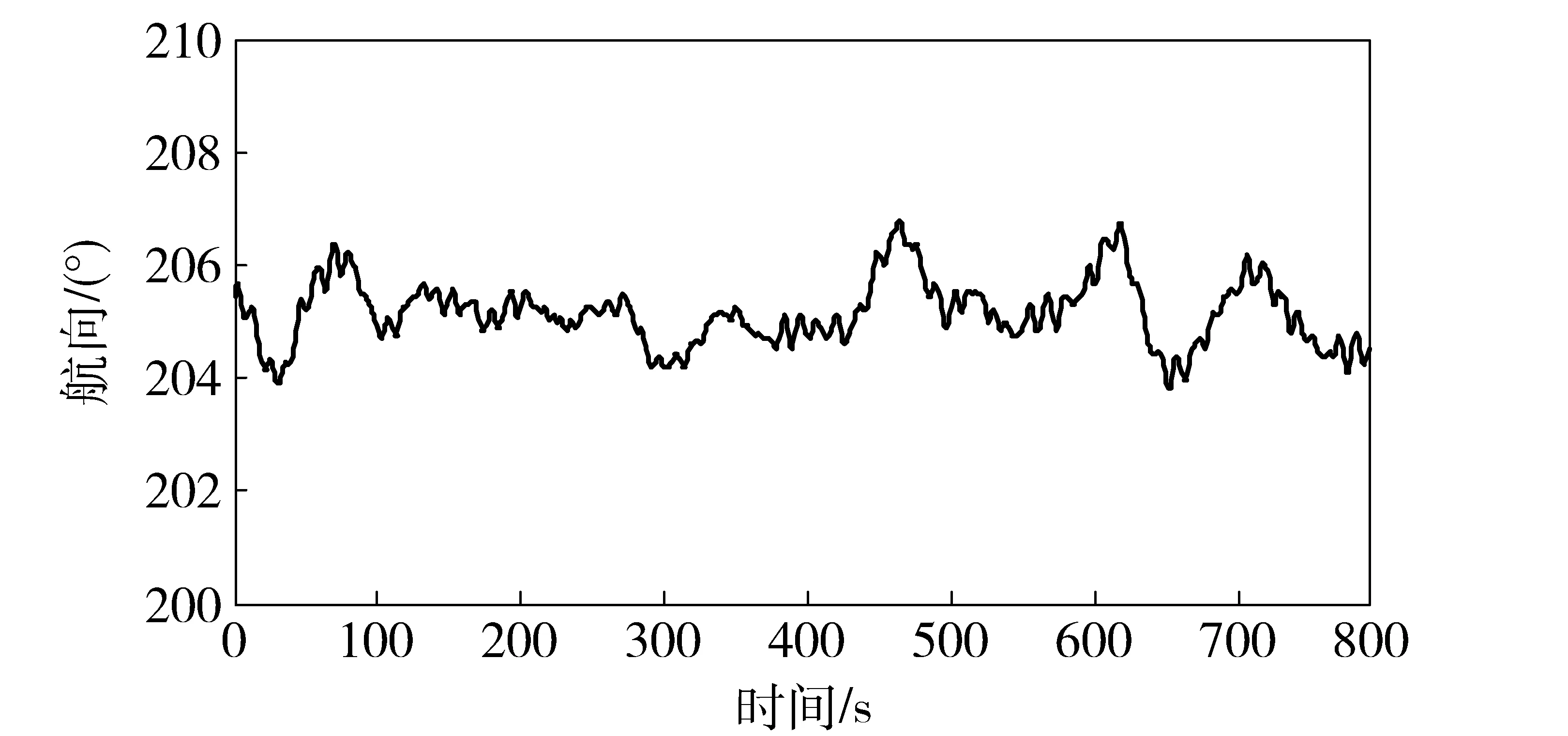
图7 观测平台航向变化图Fig.7 Change in observation platform course

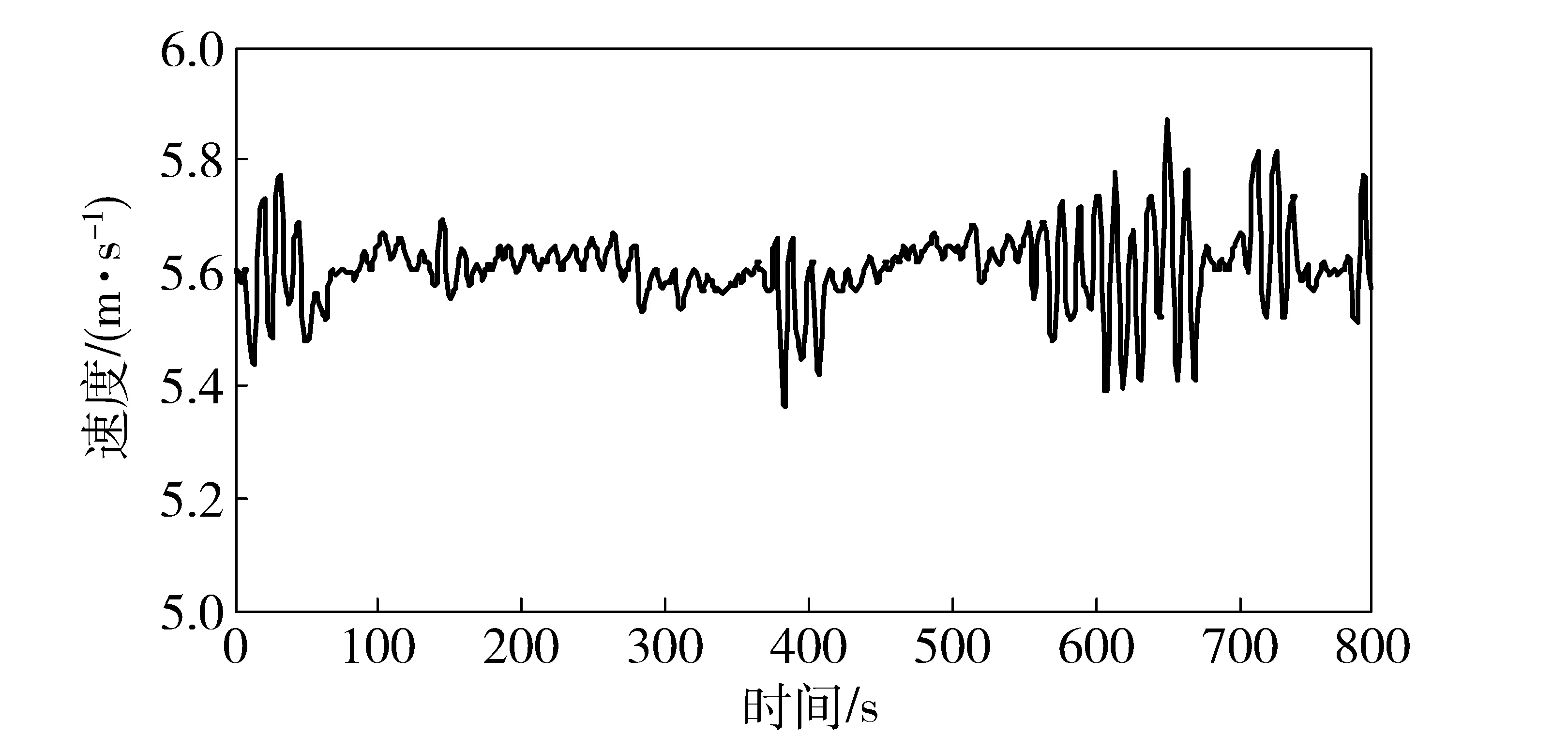
图8 观测平台航速变化图Fig.8 Change in observation platform speed

基于波束域信息，利用线谱瞬时频率跟踪提取算法，跟踪提取其中两根线谱，并将跟踪提取的线谱与目标功率谱历程进行对比，具体如图9所示。跟踪的线谱能很好地与目标的实际线谱吻合，体现了线谱瞬时频率跟踪提取的实际效果。

图9 目标谱特征提取结果Fig.9 Extracted target spectral feature

利用跟踪提取的高精度线谱解算目标运动要素，解算目标初始距离、当前距离、航速、航向如图10～图13所示。

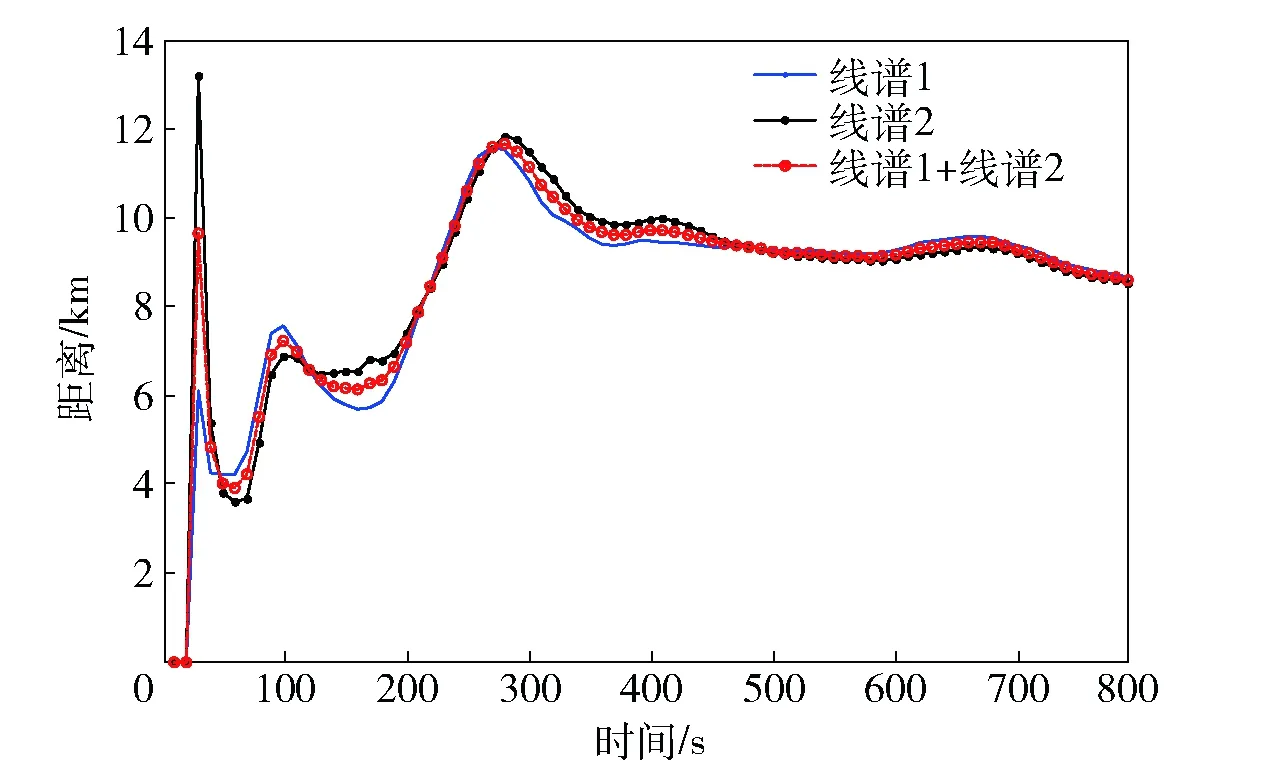
图10 波束域定位跟踪算法解算的目标初始距离结果Fig.10 Calculated initial target distances of beam target motion analysis algorithm

图11 波束域定位跟踪算法解算的目标当前距离结果Fig.11 Calculated current target distances of beam target motion analysis algorithm

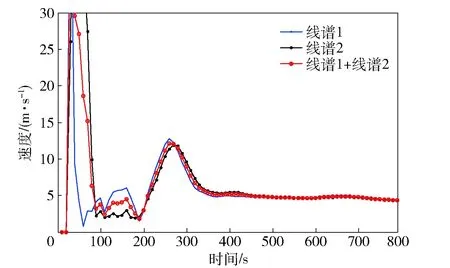
图12 波束域定位跟踪算法解算的目标航速结果Fig.12 Calculated target speeds of beam target motion analysis algorithm

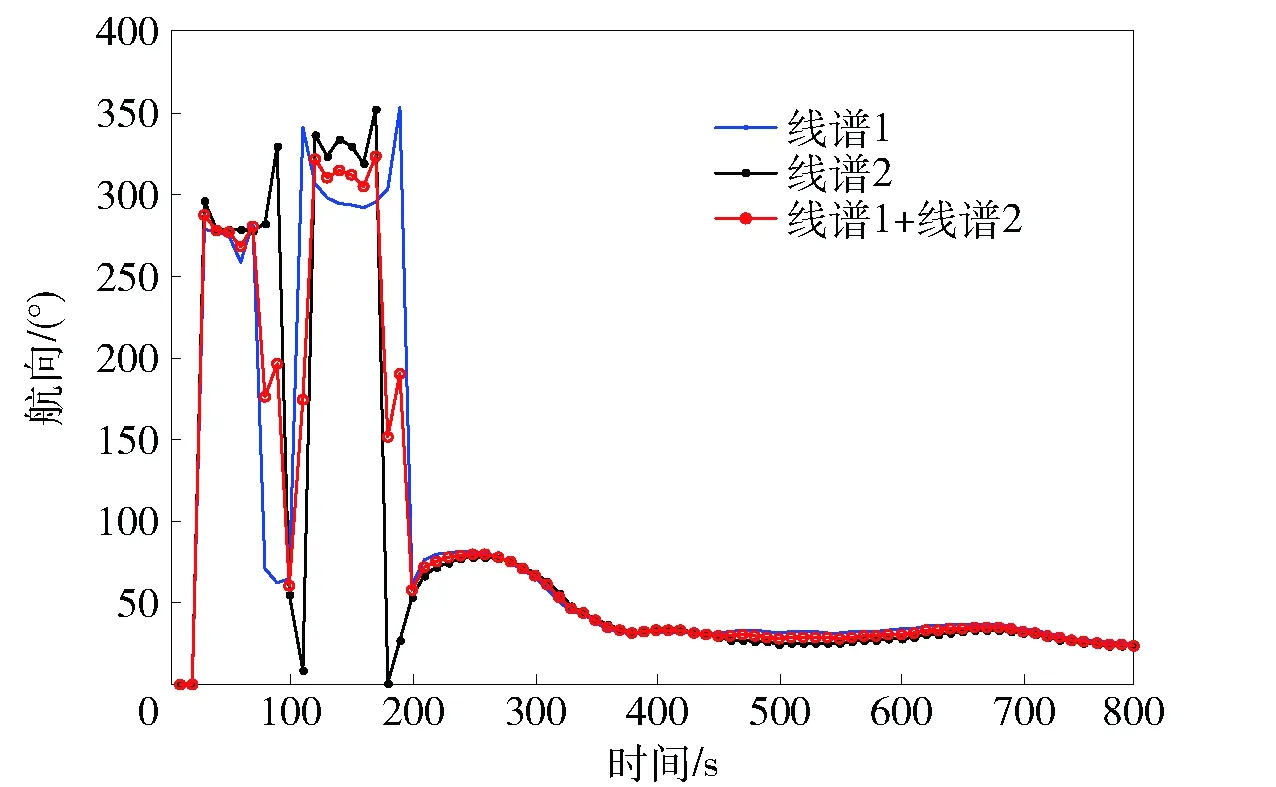
图13 波束域定位跟踪算法解算的目标航向结果Fig.13 Calculated target courses of beam target motion analysis algorithm

本航路结果表明，由于跟踪提取的线谱相对稳定，采用单线谱解算和双线谱联合解算效果基本一致，解算的目标初始距离、当前距离、航速、航向等运动参数稳定，具有较高的精度；本文所述算法在观测平台匀速直航条件下，可实现对目标的定位与跟踪，解算目标初始距离约9.8 km，本航路初始距离、航速、航向基本同时收敛，收敛时间约350 s；由于本航路观测平台未进行转向机动，传统纯方位算法难以收敛。

2.4.2 海上试验航路2

本航路目标初始距离为5 km、航速12 kn，观测平台执行推荐机动航路，观测平台航速、航向、目标谱特征提取及运动分析结果如图14～图18所示。

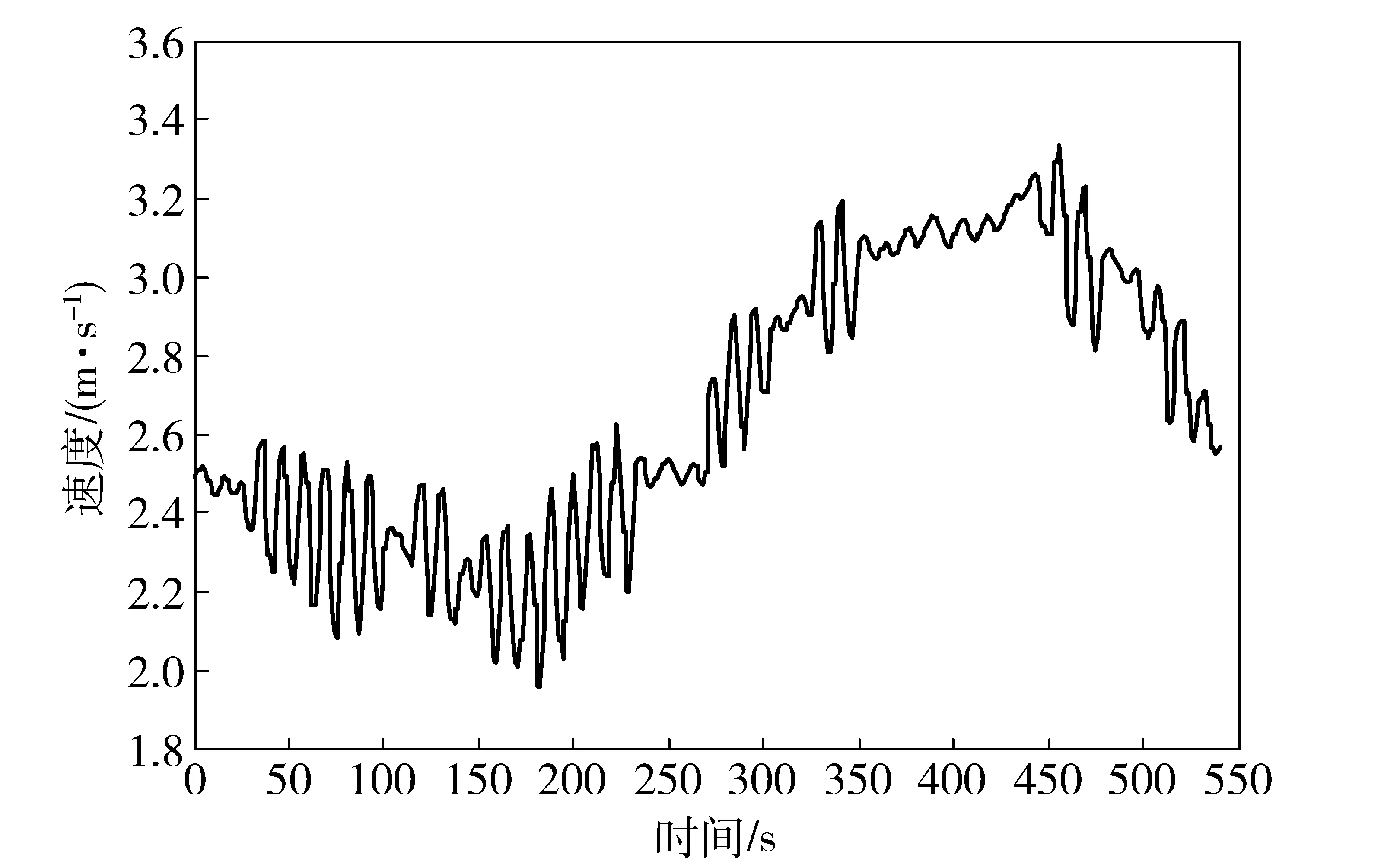
图14 观测平台航速信息变化曲线Fig.14 Change curve of observation platform speed

图15 传统算法与本文算法解算的目标初始距离对比Fig.15 Comparison of calculated initial target distance results of traditional algorithm and the proposed algorithm

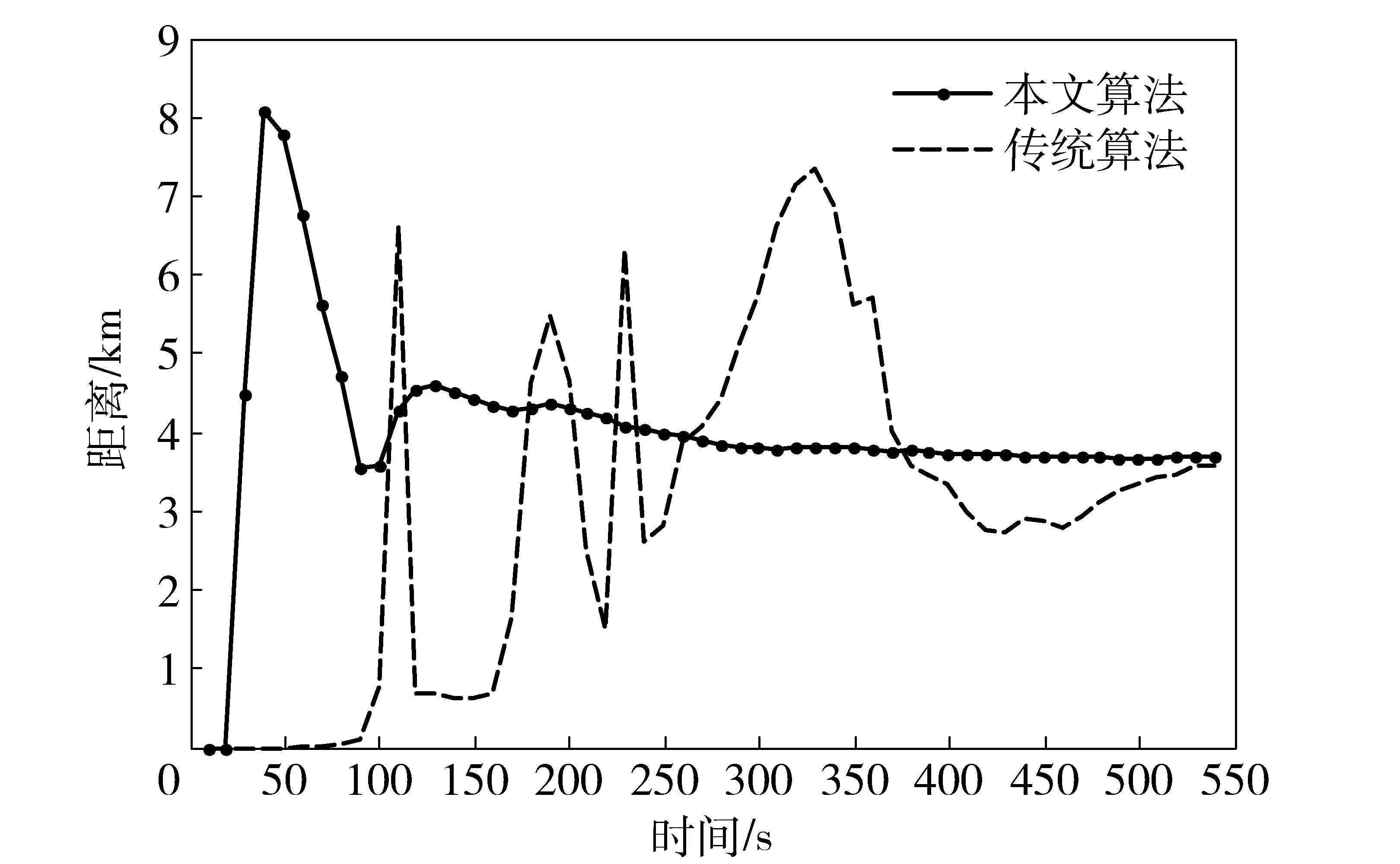
图16 传统算法与本文算法解算的目标当前距离对比Fig.16 Comparison of calculated current distance results of traditional algorithm and the proposed algorithm

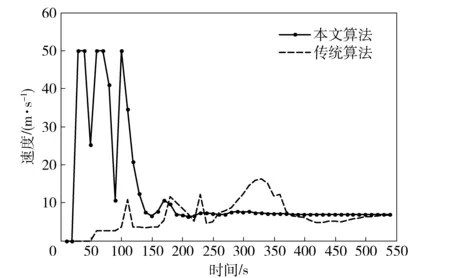
图17 传统算法与本文算法解算的目标航速对比Fig.17 Comparison of calculated target speed results of traditional algorithm and the proposed algorithm

图18 传统算法与本文算法解算的目标航向对比Fig.18 Comparison of calculated target course results of traditional algorithn and the proposed algorithm

本航路结果表明，基于声纳波束域的目标定位跟踪算法可在实现观测平台机动条件下快速解算出目标运动要素。对比传统纯方位算法，解算收敛时间大幅缩短：本次试验中传统纯方位算法收敛时间约为7 min，波束域定位跟踪算法收敛时间约为3 min. 从图15～图18中解算要素的对比图可知，波束域定位跟踪算法解算的目标距离、航速、航向波动范围小、更加稳定，进一步体现了波束域定位跟踪算法的优势和对观测平台机动的适应性。

本文算法需要目标在声纳工作频带内存在明显线谱，当某些目标线谱不明显时该算法无法使用；同时，该算法针对匀速直线航行目标当目标变速、变向时适用性不强，后续需要进一步加强研究。

3 结论

本文基于声纳目标跟踪波束信息，在波束域信息特性分析的基础上，针对匀速直线航行目标，提出了基于波束域信息的目标定位跟踪方法，完成了高精度线谱瞬时频率的跟踪提取，基于多特征观测方程实现了对目标的快速定位与跟踪。具体结论如下：

1)本文算法通过引入目标多普勒线谱特征，提高了目标的可观测性，可实现在观测平台不机动条件下对目标的定位跟踪，解决了传统方法在观测平台不机动条件下难以解算要素的难题。

2)在仿真条件下，观测平台匀速直线航行时，对于10～30 km的目标，本文算法解算收敛时间约为6.38～11.46 min.

References)

[1] Chan Y T，Rudnicki S W．Bearing-only and Doppler-bearing tracking using instrumental variables[J]． IEEE Transactions on Acoustics Speech and Signal Processing， 1992，28(4)：1076-1082.

[2] 王家鑫，李关防，袁富宇,等．声纳特征信息在舰艇信息综合处理中的应用研究[J]．指挥控制与仿真，2015，37(3)：44-51. WANG Jia-xin, LI Guan-fang, YUAN Fu-yu, et al. Application of submarine information processing system using SONAR feature information[J]. Command Control & Simulation, 2015，37(3)：44-51.(in Chinese)

[3] Becker K．A general approach to TMA observability from angle and frequency measurements[J]． IEEE Transactions on Acoustics Speech and Signal Processing， 1996，32(1)：487-496.

[4] Lu M Z，Li M，Mao W N．The detection and tracking of weak frequency line based on double-detection algorithm[C]∥Proceedings of International Symposium on Microwave， Antenna， Propagation， and EMC Technologies for Wireless Communications. Hangzhou，China: IEEE,2007：1195-1198.

[5] Ho K C, Chan Y T. An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis[J]. IEEE Transactions on Signal Processing, 2006, 54(3):809-822.

[6] 万瑾，宋志杰．基于方位和线谱频移的TMA新算法[J]．火力与指挥控制，2008，33(8)：58-61. WAN Jin, SONG Zhi-jie. A new TMA based on bearings and line Doppler shift[J]. Fire Control and Command Control，2008，33(8)：58-61. (in Chinese)

[7] 王燕，邹男，付进，等. 基于同态滤波技术的水下目标运动参数估计[J]. 兵工学报, 2014, 35(7): 1045-1051. WANG Yan，ZOU Nan，FU Jin，et al. Estimation of underwater target motion parameters based on homomorphic filtering[J]. Acta Armamentarii, 2014, 35(7): 1045-1051.(in Chinese)

[8] 刘圣松，陈韶华，陈川. 一种水下静止平台对目标运动参数的联合估计方法[J]. 兵工学报, 2016, 37(4): 684-689. LIU Sheng-song, CHEN Shao-hua, CHEN Chuan. Combined algorithm for motion parameter estimation of target on underwater static platform[J]. Acta Armamentarii, 2016, 37(4): 684-689.(in Chinese)

Passive Sonar Target Motion Analysis Based on Line-spectrum Instantaneous Frequency Estimation

LI Guan-fang, CUI Jie, YUAN Fu-yu

(Jiangsu Automation Research Institute, Lianyungang 222061,Jiangsu, China)

A new target motion analysis method based on line-spectrum instantaneous frequency estimation for passive sonar feature information is studied. The proposed algorithm combines high-accuracy instantaneous frequency tracking with target motion analysis using the target feature information to extract high-accuracy Doppler frequency and calculate the motion parameters of targets quickly. Computer simulation and sea-trial results show that the method can be used to solve the target motion analysis problem without own ship maneuver. It can reduce the calculation convergence time more than four minutes under the same maneuvering conditions.

information processing technology; target feature information; target motion analysis; motion feature extraction; passive location

2016-06-07

李关防(1982—), 男, 高级工程师，博士。E-mail: liguanfang@sina.com

TB566

A

1000-1093(2017)07-1395-07

10.3969/j.issn.1000-1093.2017.07.018