旋转稳定二维弹道修正弹在固定舵作用下的角运动特性研究

吴映锋， 钟扬威， 王良明

(1.南京理工大学 能源与动力工程学院, 江苏 南京 210094; 2.63961部队, 北京 100012; 3.中国航天科工集团公司 第九总体设计部， 湖北 武汉 430040)

旋转稳定二维弹道修正弹在固定舵作用下的角运动特性研究

吴映锋1,2， 钟扬威1,3， 王良明1

(1.南京理工大学 能源与动力工程学院, 江苏 南京 210094; 2.63961部队, 北京 100012; 3.中国航天科工集团公司 第九总体设计部， 湖北 武汉 430040)

为研究旋转稳定二维弹道修正弹在固定舵作用下的攻角及速度运动特性，建立了复数形式的角运动方程。推导了固定舵匀速转动时攻角的强迫运动解及固定舵产生阶跃激励时攻角的瞬态、稳态响应解析解；推导了有控时平均速度偏角的解析解，导出了平均偏角的幅值和相位角与固定舵参数的关系；提出了旋转稳定二维弹道修正弹在固定舵作用下的飞行稳定性条件。结果表明：二维弹道修正弹无控时应避免共振，有控时应限制攻角最大增量及平衡攻角幅值；有控时平均偏角的相位角较固定舵滚转角提前一个前置角。研究结果对旋转稳定二维弹道修正弹的飞行稳定性设计及制导方法研究提供了参考。

兵器科学与技术； 二维弹道修正弹； 角运动； 飞行稳定性； 共振； 响应谱

0 引言

随着精确打击作战理念地应用，使得对常规弹药的制导化改造成为了一种发展方向。安装固定舵的修正引信由于其低成本、小体积、通用化等优点，使其在常规弹丸的制导化改造中极具优势。

二维弹道修正弹的固定舵与修正引信体采用轴承连接，无控阶段固定舵低速旋转，修正阶段相对地面固定在某一角度，使得弹丸的动力学特性不同于传统弹丸。国内外一些学者对这方面进行了研究，取得较多成果。文献[1-2]建立了该类弹丸的角运动方程，研究了其飞行稳定性和在脉冲力作用下的运动特性。文献[3]推导了弹丸的飞行稳定性条件，并讨论了不同系数对稳定性的影响。文献[4-5]分别研究了弹丸在重力和控制力作用下的动态响应特性、强迫运动特性等问题。文献[6]研究了固定舵匀速转动和固定舵静止时弹丸的动力学特性，并给出了弹丸飞行稳定性判据。文献[7]采用霍尔维茨判据建立了弹丸的飞行稳定性判据。文献[8]采用小扰动理论建立了弹丸的飞行稳定性判据。文献[9-10]分别分析了静稳定二维弹道修正弹的稳定特性和共振特性。由于弹体高速旋转的陀螺效应，固定舵对弹丸的攻角及速度的影响比静稳定弹复杂的多，这些影响是二维弹道修正弹的关键技术—飞行稳定性设计及修正原理研究的基础，而目前这些方面的研究较少。

本文拟对固定舵作用下弹丸的攻角及速度运动特性展开研究。首先建立了在固定舵作用下的弹丸角运动方程；然后求解了弹丸无控飞行时的强迫运动解；其次推导了有控飞行时的瞬态、稳态角运动及平均偏角的解析解，得到了平均偏角的幅值与相位角的解析解；最后提出了弹丸无控飞行时应避免共振，有控飞行时应限制攻角瞬态响应的最大值，同时还应限制平衡攻角等飞行稳定性条件。

1 二维弹道修正弹角运动方程

1.1 弹丸在准弹体坐标系中的动力学方程

根据质心运动定理，推导出二维弹道修正弹在准弹体坐标系中质心运动的动力学方程为

(1)

式中：m为弹丸质量；vx4、vy4、vz4为弹丸速度矢量在准弹体坐标系上的分量；ωytan ϑ、ωy、ωz为准弹体坐标系的转动角速度，ϑ为俯仰角；Fx4、Fy4、Fz4为弹丸受到的合力在准弹体坐标系下的分量。

根据动量矩定理，可推导出二维弹道修正弹在准弹体坐标系中绕质心转动的动力学方程为

(2)

式中：ωfx、ωax分别为固定舵和弹身的转动角速度；Ifx、Iax分别为固定舵和弹身的极转动惯量；Iy为全弹的赤道转动惯量；Mfx、Max、My、Mz分别为固定舵和弹身在准弹体坐标系各轴上受到的力矩。

1.2 弹丸角运动方程

如图1所示，从速度矢量v上取距离原点O单位长度的一点R，过点R作平行于Oy4轴的线段为实轴，其正向与Oy4轴一致。再过R作平行于Oz4轴的线段为虚轴，其正向与Oz4轴相反。由实轴和虚轴可构成一复平面，弹轴与该平面的交点为B，定义复攻角为Δ，其大小和方向分别为矢量RB的大小和方向。

图1 攻角的几何描述Fig.1 Geometrical description of angle of attack

由图1可得

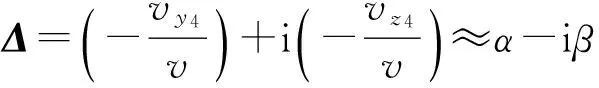
(3)

式中：α为攻角；β为侧滑角。

下面略去准弹体坐标系较小的轴向分量ωytan ϑ，将其视为非滚转坐标系，推导弹丸的角运动方程。

将(1)式的第2、第3个方程的自变量改为弹道弧长s并除以v2，得

(4)

将(4)式中第2个方程乘以虚数单位i，并与第1个方程相加，得

(5)

(6)

将(2)式的第3、第4个方程的自变量也改为弧长s，并除以v2，得

(7)

将(7)式的第2个方程乘以虚数i，并与第1个方程相加，得

(8)

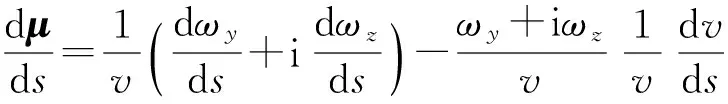
(9)

将(8)式、(9)式合并，得到复数形式的横向转动方程：

(10)

复数方程中相关的力和力矩也应该表示为复数形式。在不考虑风的影响下，将弹丸上的作用力和力矩投影到准弹体坐标系中，写成复数形式如表1所示。

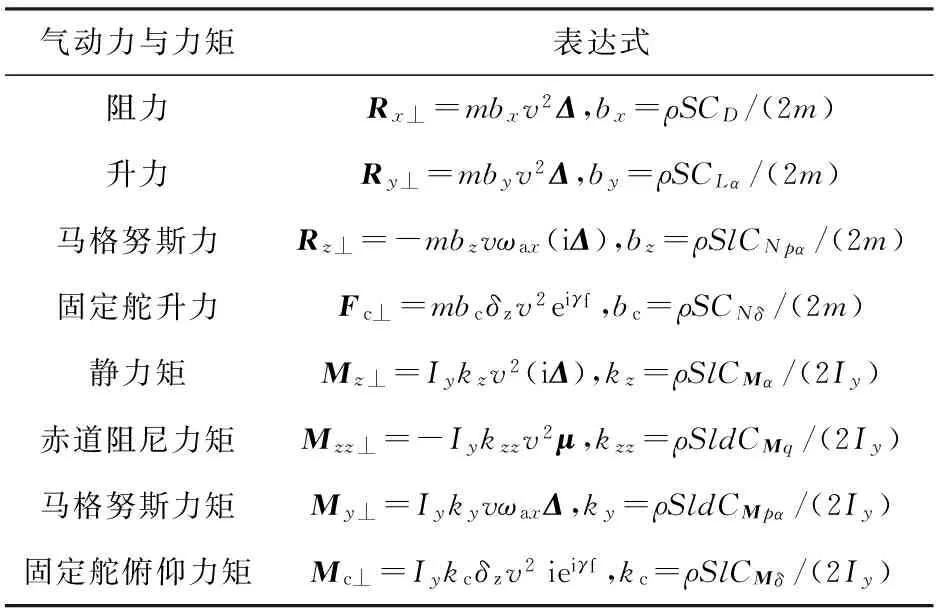
表1 气动力与力矩的复数形式

表1中：CD、CLα、CNpα、CMα、CMq、CMpα分别为弹丸的阻力系数、升力系数导数、马格努斯力系数导数、静力矩系数导数、赤道阻尼力矩系数导数、马格努斯力矩系数导数；CNδ、CMδ分别为固定舵的升力系数和俯仰力矩系数对固定舵安装角δz的导数；S、l、d分别为弹丸的参考面积、参考长度、参考直径；ρ为空气密度。

将复数形式的力和力矩代入到弹丸横向运动方程的复数方程，并用“′”表示对弧长s的导数，得

(11)

(12)

将(11)式对弧长s求一次导，得

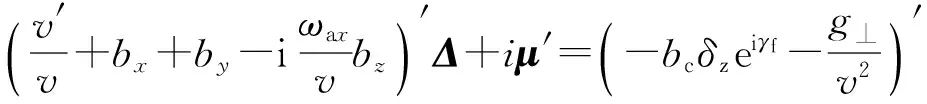
(13)

由(12)式得到μ′的表达式，并代入到(13)式，得

(14)

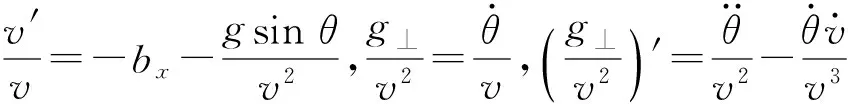
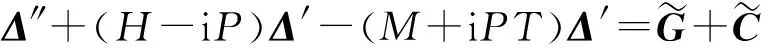
(15)

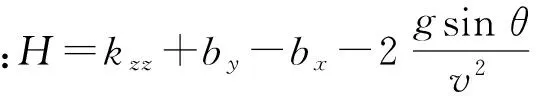
1.3 角运动方程解的形式

采用缓变系数法，角运动方程(15)式为2阶常系数非齐次线性微分方程。由常系数线性微分方程理论知，方程(15)的解由齐次解和非齐次解叠加而成。齐次解表示初始条件引起的运动，非齐次解表示由强迫因素造成的运动。因此，二维弹道修正弹角运动方程的解可分成3部分：齐次方程的通解Δ1、重力产生的动力平衡角Δp和由固定舵产生的角运动Δc. 前两个解在文献[2-3,6,11] 中都有论述，本文重点讨论第3个解Δc.

在固定舵作用下，非齐次角运动方程为

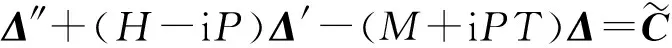
(16)

二维弹道修正弹在飞行时，固定舵大致处于两种状态，即固定舵相对地面匀速转动(无控飞行)和固定舵相对地面固定在某一方位(有控飞行)。下面分别对固定舵处于两种状态时的角运动特性进行分析。

2 无控飞行时固定舵产生的角运动特性分析

设固定舵相对地面转动的角速度为γ′f=ωfx(s)，则γf=γf0+ωfx(s)s，代入(16)式得

Δ″+(H-iP)Δ′-(M+iPT)Δ=K1eiωfx(s)s，

(17)

对于匀速不变的角速度ωfx(s)，(17)式右边是一个指数强迫函数，可采用与强迫函数相同的特解，于是(17)式的通解为

Δ=C1el1s+C2el2s+C3eiωfx(s)s，

(18)

式中：C1、C2为待定系数，由初始条件确定；l1,2=λ1,2+iω1,2的意义及计算公式参考文献[11]；C3由直接代入法求得，即

(19)

在零初始条件下，即s=0时，Δ0=0，Δ′0=0，有方程组

(20)

解(20)式得

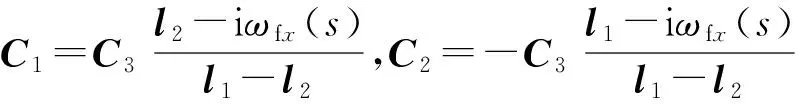
(21)

将(21)式代入到(18)式中，得到固定舵匀速转动时产生的攻角为

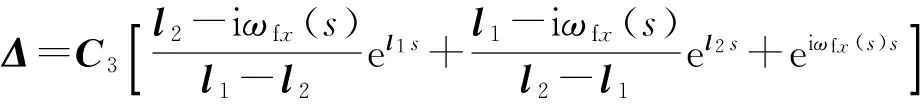
(22)

由(22)式可知，由固定舵匀速转动产生的周期性强迫干扰使得攻角的运动为3圆运动。3个圆运动的角频率分别为ω1、ω2、ωfx(s)，其中ω1、ω2为齐次方程所对应的快、慢圆运动角频率，ωfx(s)为固定舵转动产生的强迫运动角频率。

在弹道初始段，略去数值较小的阻尼因子λ1、λ2，则l1,2≈iω1,2. 对于某型旋转稳定二维弹道修正弹，在初速930 m/s，射角51°射击时，出炮口处有ω1≈0.156 rad/m，ω2≈0.024 rad/m. 若固定舵的转速为ωfx=-120 rad/s，则强迫运动的角频率ωfx(s)≈-0.129 rad/m. 将ω1、ω2、ωfx(s)代入到(20)式，得到快、慢圆运动的模分别为

C1≈1.151|C3|，C2≈2.151|C3|.

(23)

由于强迫运动的幅值与快慢圆运动相当，角频率的模介于快、慢圆运动之间，故强迫运动将显著改变攻角的二圆运动曲线，如图2所示。

图2 攻角圆运动Fig.2 Circular movement of angle of attack

随着飞行弧长增加，若弹丸满足动态稳定性条件，在阻尼因子λ1,2的作用下， (22)式的快、慢圆运动幅值逐渐衰减至消失。最后只剩下一圆强迫运动，其角频率为ωfx(s)，幅值为|C3|，如图3所示。

图3 1圆运动Fig.3 One circular movement

3 有控飞行时固定舵产生的角运动特性

为了对二维弹道修正弹的弹道进行修正，固定舵需要不时地进行滚转控制，将其固定在某个方位上，这会对弹丸的角运动产生影响。固定舵进行滚转控制时，相当于对弹丸产生了阶跃激励，下面研究弹丸在阶跃激励下攻角的响应。

当固定舵固定在某个方位时，有γf=γfc，γ′f=0 rad/s. 因此，角运动方程(16)式变为

Δ″+(H-iP)Δ′-(M+iPT)Δ=K2，

(24)

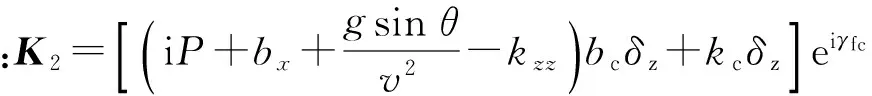
3.1 阶跃激励时角运动方程的瞬态解

固定舵产生阶跃激励时，角运动方程(24)式变为

Δ″+(H-iP)Δ′-(M+iPT)Δ=K2ε(s)，

(25)

式中：ε(s)为单位阶跃函数。

阶跃激励相当于在角运动方程等号右边突加了一个常值强迫项，可以先设立新坐标[12]为

(26)

将(26)式代入到(25)式，得

Δ″n+(H-iP)Δ′n-(M+iPT)Δn=0，

(27)

式中：初始条件为Δn0=K2/(M+iPT)，Δ′n0=0.

由(27)式可见，角运动在阶跃激励作用下的响应为初始条件为Δn0、Δ′n0的自由运动。于是得到阶跃激励作用时弹丸角运动方程的解为

(28)

在第2节的射击条件下，取弹道上某个特征点，固定舵滚转角固定在0°时，通过数值积分出来的攻角和(28)式理论推导计算出来的攻角曲线如图4所示。

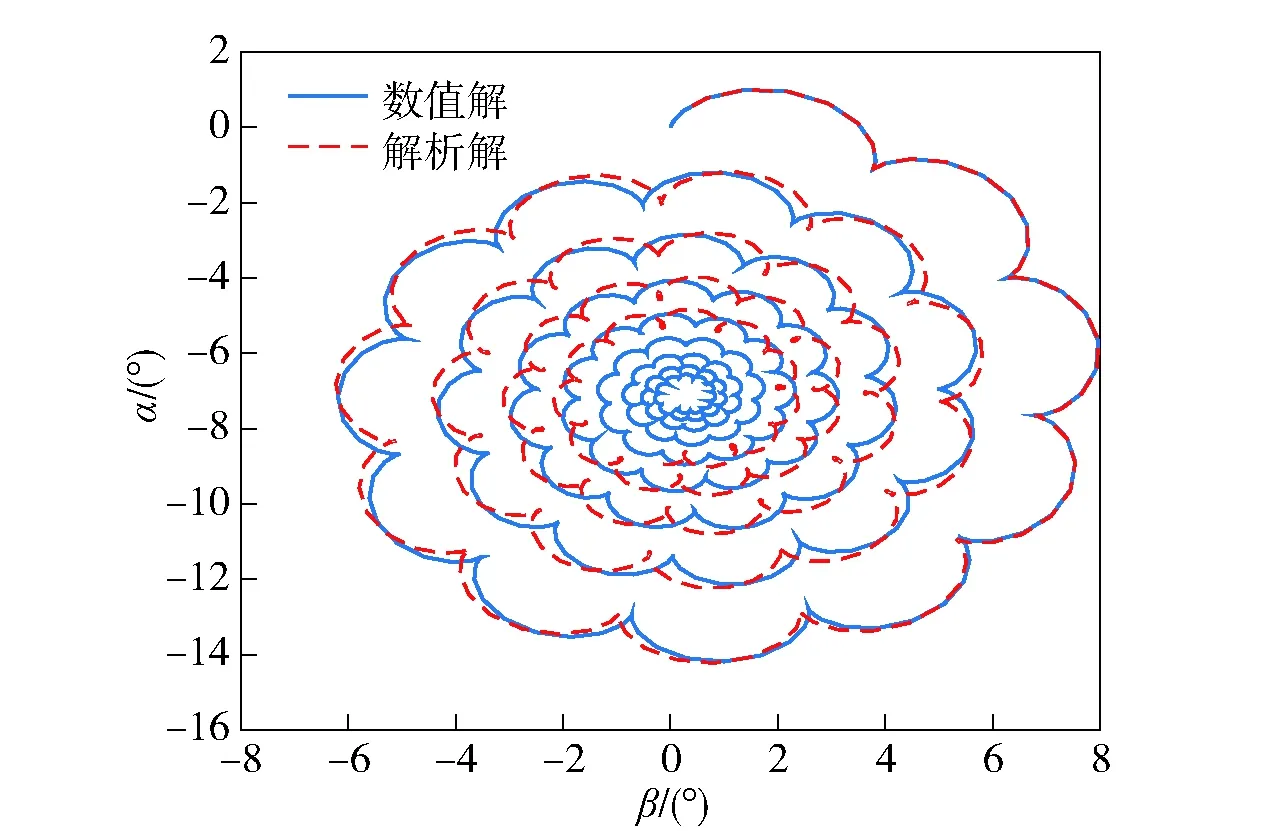
图4 数值积分和理论推导的攻角曲线Fig.4 Numerically integrated and theoretically derived attack angle curves

从图4可以看出，理论推导出的攻角和数值积分出的攻角，幅值和频率都很接近。从图4中还可以看出，与静稳定弹丸不同，二维弹道修正弹在向上的控制力作用下并不是产生向上的攻角，而是产生向下和向右的攻角。

3.2 阶跃激励时角运动方程的稳态解

在稳态飞行时，有Δ″=0、Δ′=0，代入到(24)式，得到攻角的稳态响应解为

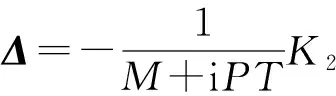
(29)

在3.1节的特征点上，固定舵滚转角固定在0°时，理论推导计算出的攻角响应瞬态解和稳态解如图5所示。

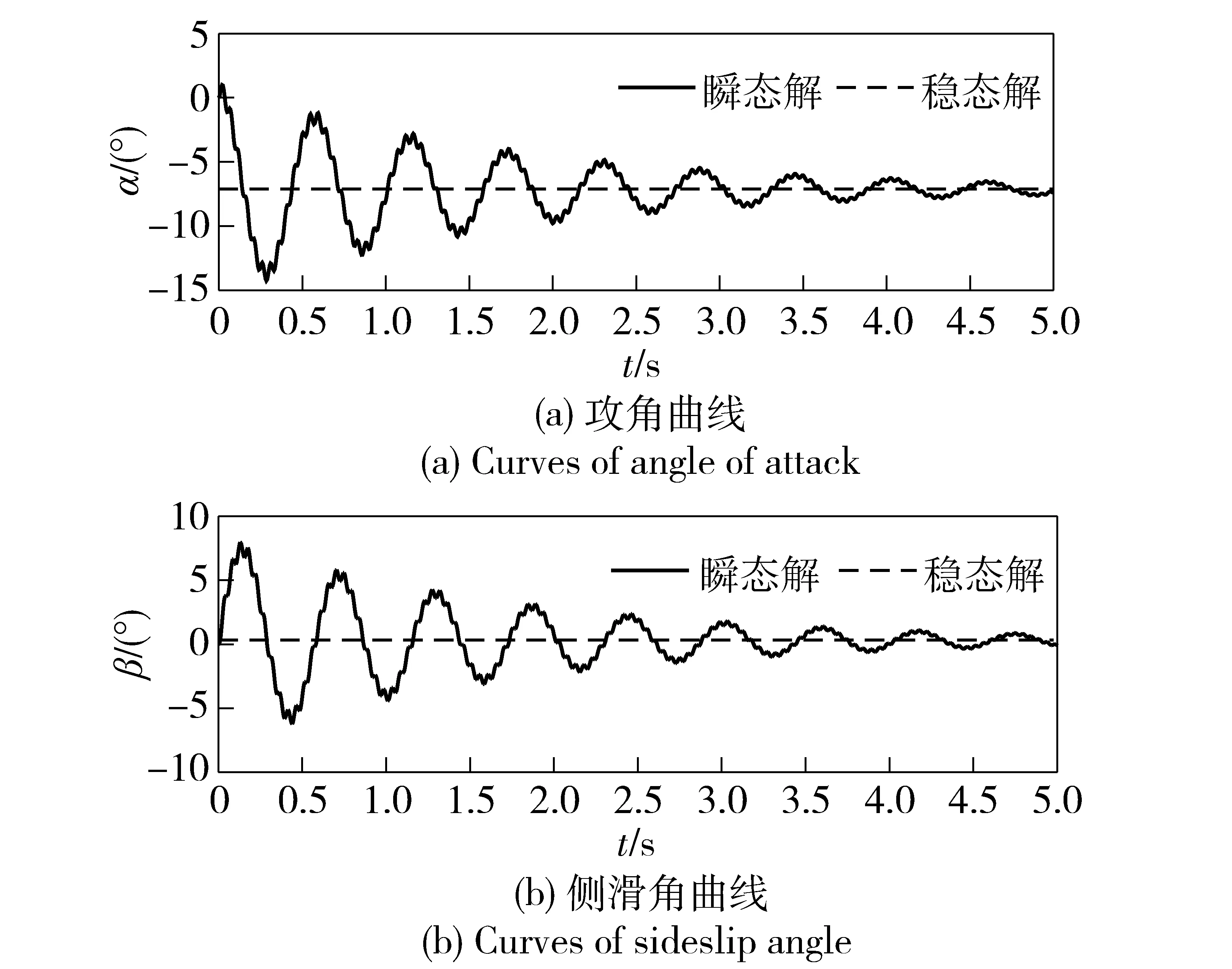
图5 理论推导的攻角瞬态解和稳态解Fig.5 Theoretically derived transient and steady state solutions of angle of attack

从图5可以看出，攻角的稳态解反映了攻角在摆动结束后的位置。

4 固定舵产生的角运动对速度方向的影响及运动机理分析

4.1 固定舵产生的角运动对速度方向的影响分析

固定舵产生控制力后，会使弹丸攻角发生变化，有了攻角就会在攻角面内产生升力。由于攻角面不断绕速度线旋转，升力方向也就不断地改变，于是速度方向也在不断旋转改变。引入复偏角Ψ=Ψ1+iΨ2(Ψ1、Ψ2分别表示速度高低角及速度方向角的增量)[11]，在攻角产生的升力和舵面产生的控制力作用下，弹丸复偏角的导数为

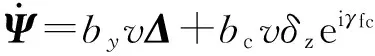
(30)

将固定舵产生阶跃激励时的攻角代入，得

(31)

将s=vt代入(31)式，并从0到t积分得

bcvδzeiγfct,

(32)

式中：el1vt和el2vt为周期衰减项，可忽略掉，只考虑偏角的平均位置。将l1+l2=-(H-iP)，l1l2=-(M+iPT)代入到(32)式，化简得

(33)

(34)

则可得

(35)

(35)式是两个很重要的公式：第1式表示偏角增量与弹丸当前飞行参数和舵偏角的关系；第2式反映了偏角的平均位置较γfc提前了χ角，χ可称为相位角φψ相对于γfc的前置角。在进行制导方法设计时，要使得速度高低角和方向角耦合修正，需考虑这个前置角。χ计算公式为

(36)

式中：

Rχ=-by·

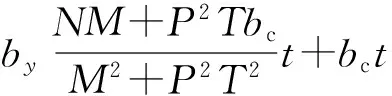
N=(bx+gsinθ/v2-kzz)bc+kc；

Iχ=-by·

图6为固定舵滚转角在0°时，数值积分和理论推导计算出的偏角及理论推导出的平均偏角。

图6 数值积分和理论推导的偏角曲线及平均位置Fig.6 Numerically integrated and theoretically derived deflection angle curves

从图6可以看出，理论计算的偏角围绕平均偏角变化，且和数值积分出的偏角比较接近。

4.2 有控时旋转稳定弹丸攻角及速度运动机理

弹丸在控制力矩作用下的摆动特性用动量矩定理描述：

(37)

高旋弹丸的动量矩为H=[Iaxωax,Iyωy,Iyωz]T，由于弹丸的旋转角速度ωax远大于其摆动角速度ωy和ωz，故弹丸的动量矩主要为大小不变的轴向动量矩。因此，在控制力矩作用下，(37)式写为

ω×H=Mc.

(38)

前面通过复攻角分析了弹丸在固定舵控制力作用下的角运动及对速度方向的影响，得出向上的控制力作用下弹丸产生向右和向下的攻角，且速度响应的平均方向比固定舵滚转角提前了χ角。下面以固定舵滚转角固定在0°时为例，根据(38)式解释这个原因。

当固定舵滚转角固定在0°时，向上的舵面升力对弹体产生了向右的俯仰力矩。根据(38)式，在该力矩作用下，弹体会产生一个向下的摆动角速度，此时，弹丸会产生向右的侧滑角βc. 由βc产生的向右升力会对弹体产生向下的力矩，该力矩对弹体产生向左的摆动角速度，因此，弹体会产生向下的攻角αc. 由于向下的αc是由向右的βc产生的，故αc滞后βc一段时间。攻角所产生的升力总是使速度方向沿攻角方向变化，因此速度方向也平均向右下方变化。尽管经过一段时间后产生向左的侧滑角，偏角也向左转动，但平均位置回不到正下方，因此形成了向右下的平均偏角，如图6所示。

在稳态情况下，弹体的摆动角速度ω趋向于0，此时由攻角αtc产生的静力矩与由固定舵产生的俯仰力矩平衡，有

(39)

可得

(40)

(40)式表示了在平衡状态下，弹丸的平衡攻角与固定舵舵偏角的关系。

5 固定舵作用下的飞行稳定性条件

5.1 无控飞行时的共振不稳定

固定舵无控时的低速旋转形成了对弹丸角运动的周期干扰，如果这个干扰频率与弹体自由摆动的频率相同，就会发生共振，共振的出现会使攻角突然增大甚至发散，造成飞行不稳定，下面讨论这种共振不稳定的特性。

将-(H-iP)=l1+l2、-(M+iPT)=l1l2代入到(19)式的分母，并分解因式，得

(41)

再将l1,2=λ1,2+iω1,2代入(41)式，求得强迫运动的幅值为

|C3|=

(42)

对于旋转稳定的二维弹道修正弹，共振条件为

(43)

因此，固定舵与弹丸旋转方向相同时可能发生共振。|C3|随固定舵转速ωfx(s)的变化趋势如图7所示。

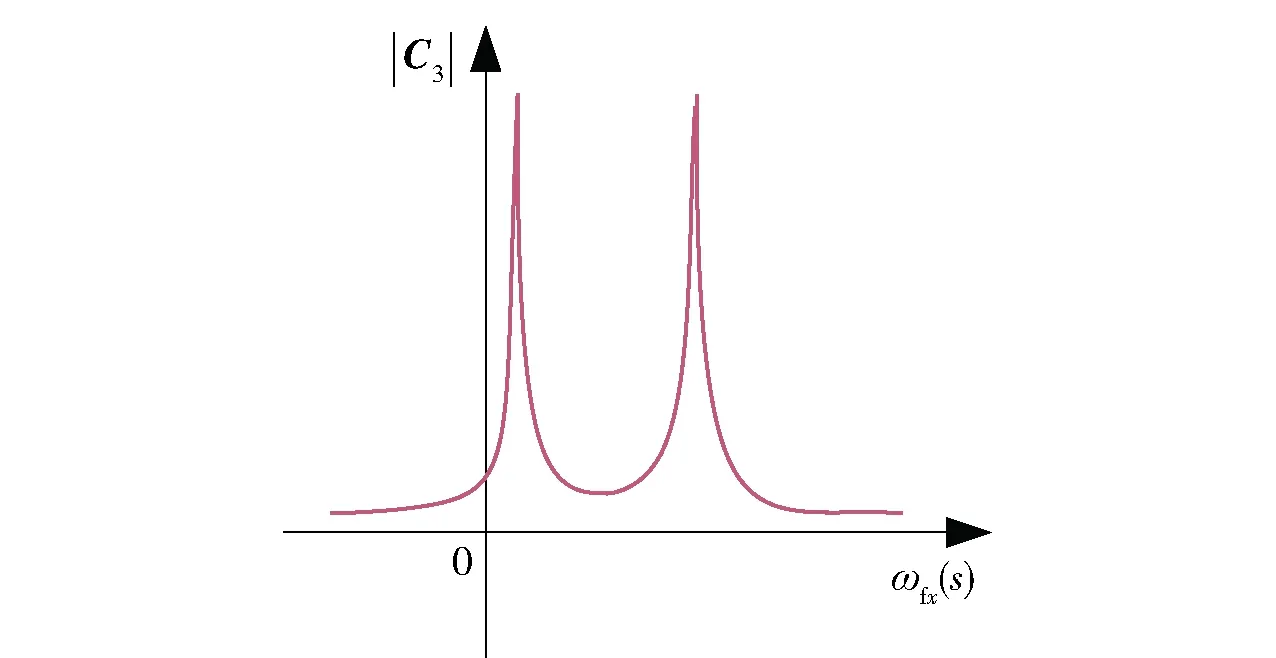
图7 强迫运动幅值的变化趋势Fig.7 Variation trends of amplitude of forced motion

下面通过数值仿真验证二维弹道修正弹存在的共振特性。对某型旋转稳定二维弹道修正弹，初速930 m/s，射角51°射击时进行7 自由度仿真。选取弹道上3个特征点，计算得到强迫运动幅值|C3|随ωfx的变化曲线(见图8)。

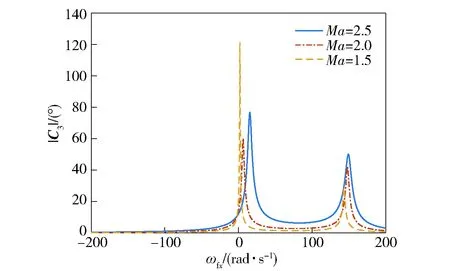
图8 强迫运动幅值的变化趋势Fig.8 Variation trends of amplitude of forced motion

从图8可以看出，3个特征点上，攻角强迫运动在ωfx>0 rad/s时都会出现两个大的幅值。

在相同的仿真条件下，固定舵转动角速度分别取-120 rad/s、-50 rad/s、-10 rad/s、10 rad/s、50 rad/s、120 rad/s时进行7自由度无控弹道仿真，全弹道上强迫运动幅值|C3|的变化如图9所示。

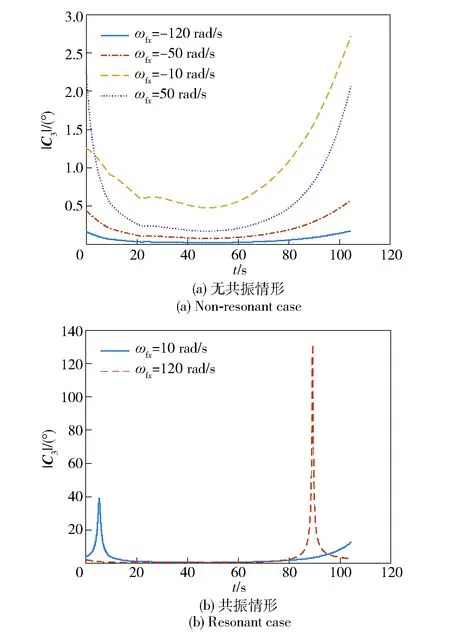
图9 不同固定舵转动角速度时全弹道攻角强迫运动幅值Fig.9 Amplitudes of forced motion during the whole trajectory at different spin rates of fixed canards

从图9中可以看出，当ωfx<0 rad/s时，攻角强迫运动幅值始终较小，且|ωfx|越大，幅值越小。当ωfx为10 rad/s和120 rad/s时，攻角会产生较大的幅值，使得弹丸飞行时间和射程减小。

当ωfx为120 rad/s时，全弹道攻角快、慢圆运动频率ω1、ω2如图10所示。

图10 全弹道攻角快、慢圆运动频率Fig.10 Fast and slow circular motion frequencies of angle of attack during the whole trajectory

从图10中可以看出，当ωfx=120 rad/s时，快圆运动的频率在89 s附近穿越120 rad/s，攻角会产生较大幅值，验证了图9的结论。

5.2 有控飞行时的瞬态攻角限制

在受到阶跃激励后，攻角通常会产生一个较大的峰值，在第5.1节的3个特征点上，计算得到的阶跃响应曲线如图11所示。

图11 攻角阶跃响应曲线Fig.11 Step response curves of angle of attack

在弹丸的飞行稳定性设计中，需要将攻角响应的最大幅值限制在一定的范围内[13]。这时，研究攻角的响应谱就很有必要。计算攻角响应谱时，可忽略阻尼项λ1,2，使计算结果更加安全。(28)式可写为

(44)

对于旋转稳定的二维弹道修正弹，一般有ω1≫ω2，故攻角响应最大值主要由慢圆运动频率决定。设慢圆运动的周期T2=2π/ω2，因此攻角最大值出现在s=T2/2处，最大值为

(45)

图12给出了全弹道上攻角对阶跃激励的响应谱。

图12 攻角响应谱Fig.12 Response spectrum of angle of attack

由图12可以看出，固定舵产生阶跃激励时，全弹道上攻角响应谱的最大值超过15°.

设二维弹道修正弹允许的最大攻角幅值增量为δmax，则有

|Δ|max≤δmax.

(46)

(46)式可以看成是二维弹道修正弹在控制力作用下的稳定性条件。

5.3 有控飞行时的稳态攻角限制

为了避免弹丸长时间以较大的平衡攻角飞行，还需对攻角的稳态响应解加以限制。对于(29)式，忽略掉较小的力和力矩，则

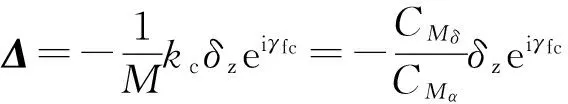
(47)

(47)式是二维弹道修正在控制力矩作用下的平衡条件，即固定舵产生的俯仰力矩和弹体攻角产生的静力矩平衡，(40)式也得出了这个结论。-CMδ/CMα是一个比较重要的参数，因为二维弹道修正弹没有姿态稳定系统，只能通过限制攻角的最大值来保证飞行稳定。由于弹丸的静力矩系数导数一般变化不大，因此，为了使稳态攻角的模|Δ|在限定的范围内，需要合理地设计固定舵的俯仰力矩系数。

6 结论

本文以安装固定舵修正引信的旋转稳定二维弹道修正弹为研究对象，推导了弹丸角运动方程，深入研究了弹丸在固定舵作用下的角运动特性，得到了以下结论：

1)固定舵匀速旋转时攻角的强迫运动特性为由3圆运动逐渐变为1圆运动，此时固定舵转速接近弹丸自由运动频率会出现共振，导致飞行不稳定，应避免出现这种情况。

2)固定舵产生阶跃控制激励时，理论推导了攻角的瞬态和稳态响应解析解，数值仿真可以看出这两个解析解的精度较高。

3)固定舵产生阶跃控制激励时，平均偏角的相位角较固定舵的滚转角提前了一个前置角，在进行制导方法设计时，应考虑这个前置角。

4)为保证弹丸有控时稳定飞行，首先应限制最大攻角幅值增量，可以根据本文提供的响应谱公式计算得到；其次应限制平衡攻角的大小，通过设计固定舵的俯仰力矩系数实现。

本文的研究结果对二维弹道修正弹的气动设计、飞行稳定性设计及制导原理方法研究具有一定的意义。后续的工作是在本文的基础上进行基于速度方向修正的制导方法研究。

References)

[1] Costello M, Peterson A. Linear theory of a dual spin projectile in atmospheric flight[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(5):789-797.

[2] Burchett B, Peterson A, Costello M. Prediction of swerving motion of a dual-spin projectile with lateral pulsejets in atmospheric flight[J]. Mathematical and Computer Modelling, 2002, 35(7):821-834.

[3] Wernert P. Stability analysis for canard guided dual-spin stabilized projectiles[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Chicago, IL, US:AIAA, 2009.

[4] Chang S J. Dynamic response to canard control and gravity for a dual-spin projectile[J]. Journal of Spacecraft and Rockets, 2016, 53(3):558-566.

[5] 常思江, 王中原, 刘铁铮. 鸭式布局双旋稳定弹强迫运动理论研究[J]. 兵工学报, 2016, 37(5): 829-839. CHANG Si-jiang, WANG Zhong-yuan, LIU Tie-zheng. A theoretical study of forced motion for dual-spin-stabilized projectiles with canards[J]. Acta Armamentarii, 2016, 37(5):829-839.(in Chinese)

[6] 许诺, 于剑桥, 王亚飞, 等. 固定翼双旋弹动力学特性分[J]. 兵工学报, 2015, 36(4): 602-609. XU Nuo, YU Jian-qiao, WANG Ya-fei, et al．Analysis of dynamic characteristics of fixed-wing dual-spin projectile[J]. Acta Armamentarii, 2015, 36(4):602-609. (in Chinese)

[7] Zhu D L, Tang S J, Guo J, et al. Flight stability of a dual-spin projectile with canards[J]. Journal of Aerospace Engineering, 2015, 229(4):703-716.

[8] 王毅, 宋卫东, 郭庆伟, 等. 固定鸭舵式二维弹道修正弹稳定性分析[J]. 军械工程学院学报, 2015, 27(3): 16-23. WANG Yi, SONG Wei-dong, GUO Qing-wei, et al. Stability analysis of two-dimensional trajectory correction mortar with fixed-canard[J]. Journal of Ordnance Engineering College, 2015, 27(3): 16-23. (in Chinese)

[9] 李伟, 王志刚. 双旋制导火箭弹运动特性分析[J]. 固体火箭技术, 2014, 37(2):143-149. LI Wei, WANG Zhi-gang. Analysis of motion characteristics for dual-spin projectile[J]. Journal of Solid Rocket Technology, 2014, 37(2):143-149. (in Chinese)

[10] 张衍儒, 肖练刚, 邱奕, 等. 双旋静稳定弹的共振不稳定研究[J]. 航天控制, 2016, 34(3):31-35. ZHANG Yan-ru, XIAO Lian-gang, QIU Yi, et al. Research on resonance instability of dual-spin static stability projectile[J]. Aerospace Control, 2016, 34(3):31-35. (in Chinese)

[11] 韩子鹏. 弹箭外弹道学[M].北京: 北京理工大学出版社, 2008: 260-280. HAN Zi-peng．Exterior ballistics of shells and rockets[M]. Beijing: Beijing Institute of Technology Press, 2008: 260-280.(in Chinese)

[12] 倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1988: 136-151. NI Zhen-hua. Vibration mechanics [M]．Xi’an: Xi’an Jiaotong University Press, 1988: 136-151.(in Chinese)

[13] 王中原, 丁松滨, 王良明. 弹道修正弹在脉冲力矩作用下的飞行稳定性条件[J]. 南京理工大学学报, 2000, 24(4): 322-326. WANG Zhong-yuan, DING Song-bin, WANG Liang-ming. Flight stability condition for a projectile of corrected trajectory with impulse moments[J]. Journal of Nanjing University of Science and Technology, 2000, 24(4): 322-326. (in Chinese)

Study on Angular Motion Characteristics of Spin-stabilized 2D Trajectory Correction Projectile under the Effect of Fixed Canards

WU Ying-feng1,2， ZHONG Yang-wei1,3， WANG Liang-ming1

(1.School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China; 2.Unit 63961 of PLA, Beijing 100012, China; 3.The 9th General Department, China Aerospace Science and Industry Corporation, Wuhan 430040, Hubei, China)

An angular motion equation in complex form is established to study the angle of attack and velocity characteristics of spin-stabilized 2D trajectory correction projectile under the effect of fixed canards. The solution of forced motion when the canards spin at a constant rate and the analytical solutions of transient and steady state responses when the canards generate step excitation are both derived. The relationships between the amplitude and phase angle of average deflection angle and the parameters of the fixed canards are presented by deriving the analytical solutions of average velocity deflection angle. The flight stability conditions of spin stabilized 2D trajectory correction projectile under the effect of fixed canards are proposed. The result shows that the projectile should avoid resonance without control, and should limit the maximum increment of angle of attack and the equilibrium angle of attack with control. In addition, the phase angle of average deflection angle has a lead angle ahead of the roll angle of fixed canards. The results provide some references for the studies of flight stability and guidance method of spin-stabilized 2D trajectory correction projectile.

ordnance science and technology; two-dimensional trajectory correction projectile; angular motion; flight stability; resonance; response spectrum

2016-10-11

武器装备预先研究项目(9140C300305140C30140)

吴映锋(1972—), 男, 高级工程师。E-mail: wuyingfeng911@126.com

TJ012.3+3

A

1000-1093(2017)07-1263-10

10.3969/j.issn.1000-1093.2017.07.003