考虑维修优先权的多状态冷储备系统可靠性模型

陈童, 狄鹏, 尹东亮

(海军工程大学 管理工程系， 湖北 武汉 430033)

考虑维修优先权的多状态冷储备系统可靠性模型

陈童, 狄鹏, 尹东亮

(海军工程大学 管理工程系， 湖北 武汉 430033)

针对多状态两部件冷储备系统存在多类维护方式的情况，假设系统中的单维修台能够根据部件状态提供保养和维修两类服务，其中维修具有更高的优先级。采用连续Phase-type分布代替指数分布等典型分布，描述工作部件在不同性能水平的停留时间、维修台保养和维修时间。利用矩阵解析方法获得了系统稳态概率，推导出系统稳态可用度、系统工作时间、系统平均停机间隔时间、维修台故障件到达率和系统故障率等参数的解析表达式。通过算例验证了模型的正确性和适用性，演示了保养和维修速率对系统各可靠性参数的影响。研究结果表明，利用Phase-type分布对多状态系统开展可靠性解析建模，能够在确保良好解析特性的同时，有效提升模型的描述能力，从假设条件环节保证模型具有更强的通用性。

兵器科学与技术； 多状态； 冷储备系统； 优先权； 可靠性； Phase-type分布

0 引言

舰船装备为了提高系统可靠性，常常对关键设备采用“用一备一”的冷储备结构，例如动力系统中的燃油、滑油子系统往往设计有备用泵组，电力系统需要设置前、后电站和前、后主配电板等。这些具有复杂结构和功能的关键设备，其性能和故障模式往往会随着使用时间、强度和外部环境的变化，表现出多样性的特点。在分析系统可靠性规律时，如果只是简单地将系统状态分为“运行”和“故障”两大类，显然不能获得准确的系统可靠性指标[1-2]。因此，多状态系统(MSS)可靠性理论[3-4]在20世纪80年代初步建立，受到国内外研究者的广泛关注。

对于多状态系统，除了通过冗余结构提升系统的任务可靠性，根据系统状态选择合适的维修活动也能确保装备获得理想的可靠性指标。常见的维修活动包括日常保养和事后维修等，不同种类的维修工作对装备性能和安全的重要程度各不相同，表现出不同的优先级别。例如，装备故障后的维修工作一般要优先于日常保养活动，因此建模时考虑优先权的存在更符合现实情况。

Zhang等[5-6]采用几何过程描述了两部件冷储备系统中部件维修活动的变化规律，考虑特定部件具有优先使用权时的情况，分析了不同维修策略对系统可靠性和经济性的影响。Leung等[7]采用类似思路研究了该类系统中特定部件具有维修优先权的情况。Yuan等[8]研究了两部件温储备系统中特定部件具有优先使用权、部件转换开关具有优先维修权，两个不同部件和转换开关的工作和维修时间均服从指数分布的系统可靠性问题。Reetu等[9]在考虑维修优先权的情况下，假设部件工作时间、预防性维修和更换时间服从负指数分布，研究了两部件并联系统的两状态可靠性问题。Kumara等[10]针对重要计算机系统采用故障修理、换件和预防性维修等多种模式的情况，研究了冷储备系统中H/W部件预防性维修具有优先权，部件失效服从负指数分布，而换件时间、修复时间以及预防性维修时间均为任意分布的问题。

在可修系统可靠性解析建模工作中，引入多状态和优先权将会显著增加分析难度。因此上述研究假设部件使用寿命、维修时间等随机变量服从指数分布等典型分布[11-12]。这种做法在一定程度上牺牲了模型的真实性和实际应用价值，才换得解析计算的便捷，也使得这些给定了精确分布函数表达形式的模型只能适用于一些特定问题。

因此，本文引入Phase-type分布，采用解析方法研究多状态两部件冷储备系统考虑维修优先权时的可靠性规律。Phase-type分布易于解析建模，可用来描述相当广泛的随机现象，便于计算，已成为一种优良的随机建模工具[13]。Neuts等[14]最早将Phase-type分布应用到可靠性随机建模工作中，假设两部件系统的失效时间服从连续Phase-type分布。Segovia等[15]研究了多状态系统受到的外部冲击间隔时间和冲击强度均服从Phase-type分布时的系统可靠性。Yu 等[16]采用Phase-type分布描述了部件工作寿命、维修时间和备件订货时间，并结合几何过程研究了部件修理后性能出现退化时的系统可靠性。Montoro-Cazorla等[17]研究了两部件冷储备系统的可靠性规律，模型考虑修复性维修和预防性维修两种维修模式；其中系统性能不断退化，退化时间服从一般分布，用Phase-type分布形式表示。陈童等[18]将部件在工作状态、储备状态和维修状态的停留时间均表示为Phase-type分布，从而获得了表决(n中取k)系统的可靠性指标。狄鹏等[19]假设系统工作和维修时间服从连续Phase-type分布，研究了具有不同维修效果的多状态可修系统可靠性问题。Li等[20]研究了温储备系统存在维修资源调度情况的系统可靠性问题，将部件寿命、储备时间、维修台休假时间均描述为连续Phase-type分布，分析了装备保障模式对系统可靠性的影响。

本文针对考虑维修优先权的多状态冗余系统可靠性解析建模工作遇到的假设条件过于严格、模型结论适用性窄的问题，利用连续Phase-type分布描述工作设备在多个性能水平的停留时间、保养时间和维修时间。假设系统具有单个维修台，维修比保养具有更高优先级，建立了一种描述能力更强的系统可靠性模型，给出了系统稳态可用度、系统工作时间、系统平均停机间隔时间、维修台故障件到达率和系统故障率等参数的解析表达式。

1 连续Phase-type分布

定义1[21][0,+∞)上的概率分布函数F(·)称为Phase-type分布，并具有m阶(α,T)表示，当且仅当它是一个有限状态Markov过程的吸收时间分布，有分布函数：

F(t)=1-αexp (Tt)eT，

(1)

式中：α=(α1,…,αm)，且满足αeT+αm+1=1；T=(Tij)为m阶方阵，Tij≥0(i≠j,i、j=1,…,m)表示从瞬态i至瞬态j的转移率，且满足Tii<0；t表示吸收时间；e为元素值均为1的行向量。

该Markov过程具有状态集{1,…,m,m+1}，状态1,…,m都是非常返的(瞬态)，状态m+1是吸收态，初始概率为(α,αm+1)，该Markov过程无穷小生成元Q可写为

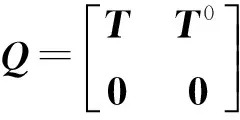
(2)

下面给出Kronecker乘积和Kronecker和的定义，这两者在后面的模型中被大量使用。

定义2[22]若A和B分别为m1×m2和n1×n2的矩阵，则它们的Kronecker乘积A⊗B为m1n1×m2n2的矩阵，且

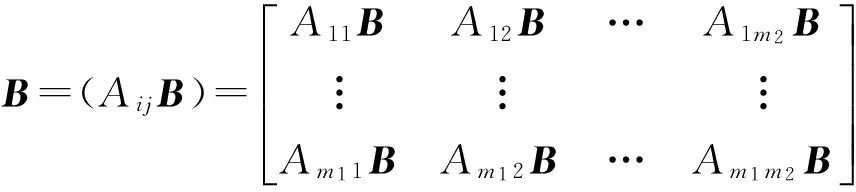
(3)

定义3[22]若A和B分别为m和n阶方阵，则定义Kronecker和为

A⊕B=A⊗In+Im⊗B，

(4)

式中：Im和In分别为m阶和n阶单位矩阵。

2 问题描述

某冷储备系统包含两台相同设备和一个维修台，每台设备性能均可以分为n+1个水平，表示成状态集S={1,…,m,m+1,…,n,n+1}. 可以将S划分为3大类：1)完好状态，即设备性能保持在设计指标附近，有状态集S1={1,…,m}；2)一般状态，即设备可以运行，但性能较差，有状态集S2={m+1,…,n}；3)故障状态，指设备发生停机故障，无法使用，有状态集S3={n+1}.

令pij(1≤i,j≤n)表示设备从性能i下降到j的概率。在使用过程中，设备性能只会不断降低，因此当i≥j时有pij=0，可知矩阵P=(pij)为上三角阵。令pi(n+1)(1≤i≤n)表示设备从性能i直接转入故障状态的概率，记矩阵P0=(pi(n+1)).

维修台可以进行保养和维修两种活动，其中维修具有更高的优先级。例如，当设备1处于状态j(j∈S2)时，若此时维修台空闲，则可为该设备提供保养服务。若维修台开展保养活动时设备2进入故障状态，则维修台立即对故障设备进行维修，而设备1则从状态j′转入运行状态。可以认为设备1此时的状态与保养前持平或有改善，即1≤j′≤j. 设备在完成保养或维修活动后，性能均恢复到完好状态。

因为设备在性能水平i(1≤i≤n)的停留时间以及保养和维修时间的分布情况往往是不确定的，因此不妨假设三者均服从一般分布，表示为Phase-type分布形式，做如下进一步假设：

1)设备在性能水平i(1≤i≤n)的停留时间相互独立，表示为ki阶PH(αi,Ti)分布；

2)设备保养和维修时间相互独立，保养时间分布表示为kM阶PH(β,U)，维修时间分布表示为kR阶PH(γ,R)；

3)设备从性能水平j进入保养，若保养活动处于y(1≤y≤kM)位相时被中止，则设备进入性能水平j′的概率矩阵为G(y,j,j′)；

4)维修台对于故障设备采取先到先服务准则。

3 模型分析

3.1 系统状态空间

该系统状态空间可以划分为

Ω=H1∪H2∪H3∪H4∪H5∪H6.

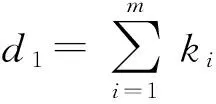
3.2 无穷小生成元

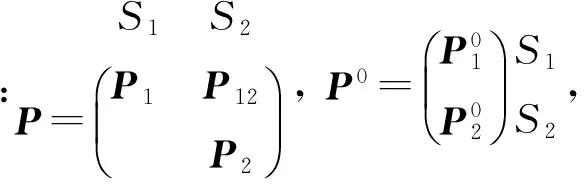
当保养活动被中止后，根据设备所处性能水平1≤j′≤m和m+1≤j′≤n，可以将矩阵G(y,j,j′)划分为G=(G1,G2).

根据3.1节的系统状态空间分类，可以将系统无穷小生成元写为

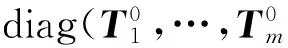
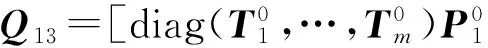
Q21表示系统从状态空间H2转移到H1，说明保养工作结束，该部件进入冷储备状态，因此有Q21=Id1⊗U0⊗en-m.

同理可知：Q31=Id1⊗R0；Q42=[(α1⊗β)⊗diag(ekm+1⊗U0⊗en-m,…,ekn⊗U0⊗en-m),0]；Q52=[(α1⊗β)⊗diag(ekm+1⊗R0,…,ekn⊗R0),0]；Q63=[R0⊗α1⊗γ,0].

4 系统特性

4.1 稳态概率向量

当系统进入稳态后，由方程组

πQ=0,πeT=1，

(5)

可得各状态空间对应的稳态概率向量[21]π=(π1,π2,π3,π4,π5,π6).

4.2 系统稳态可用度

获得系统稳态概率向量后，可知系统的稳态可用度为系统不处于状态空间H6的概率，因此有

(6)

4.3 系统工作时间

当系统进入稳态后，工作时间周期就是系统离开状态空间H6到再次进入H6的时间间隔。

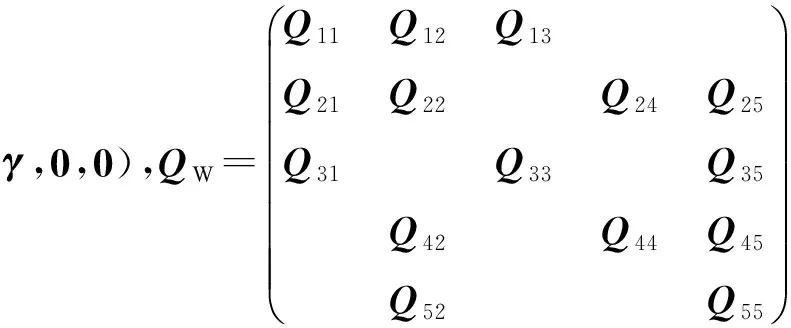
证明 由系统工作时间周期的定义知，当系统离开状态空间H6后，系统开始工作；当系统再次进入H6时，系统停机；因此可以将状态空间H6视为系统工作时间的一维吸收态。由Phase-type分布定义可知，系统工作时间周期服从Phase-type分布，且有η=(0,0,α1⊗γ,0,0)，QW为去掉Q中对应状态空间H6的行和列后所得。定理得证。

4.4 维修台故障件到达率

维修台的故障件到达率是系统内所有设备发生故障的速率之和，记为r. 在获得系统稳态概率后，可知

r=π1Q13e+π2Q25e+π3Q36e+π4Q45e+π5Q56e=

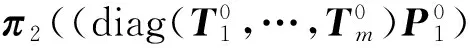
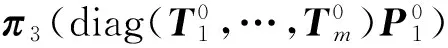
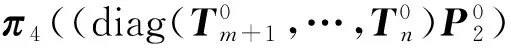
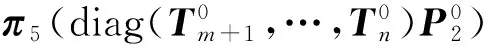
(7)

4.5 系统故障率

系统故障率是单位时间内系统进入停机状态的次数，记为rS. 可知系统只能从状态空间H3或H5进入停机状态H6，则有

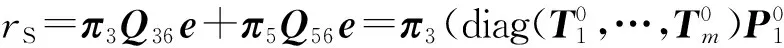
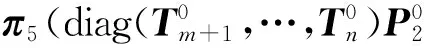
(8)

5 算例

本文算例在Intel 2.3 GHz处理器、3 GB内存的计算机上运用Matlab运算获得。

已知某系统中设备具有9个性能水平，其中完好状态为S1={1}，一般状态为S2={2,…,8}，故障状态为S3={9}，设备在各工作状态停留时间的分布如表1所示。

表1 设备在各工作状态的停留时间分布

由此可得：系统可用度为A=0.975 5；系统平均停机间隔时间为μ=1.078 3单位时间；维修台的故障件到达率为r=0.003 8次/单位时间；系统故障率为rS=0.001 6次/单位时间。

由算例可知，当设备在各性能水平的停留时间、设备保养和维修时间服从不同类型的分布时，模型能够有效获取系统的各种可靠性参数，适用性得到了显著提高，并且矩阵形式的模型参数并不会对计算效率产生明显影响。

为了直观演示保养时间对系统可靠性的影响，令保养时间服从指数分布，计算结果如图1～图4所示。

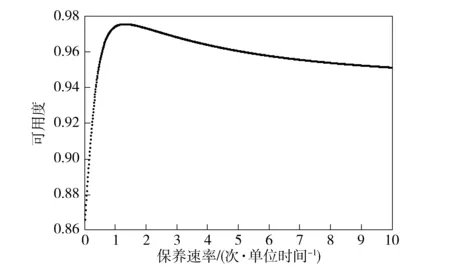
图1 保养速率对可用度的影响Fig.1 Relationship of preventive maintenance rate and system stationary availability

图2 保养速率对系统平均停机间隔时间的影响Fig.2 Relationship of preventive maintenance rate and mean time between system halt

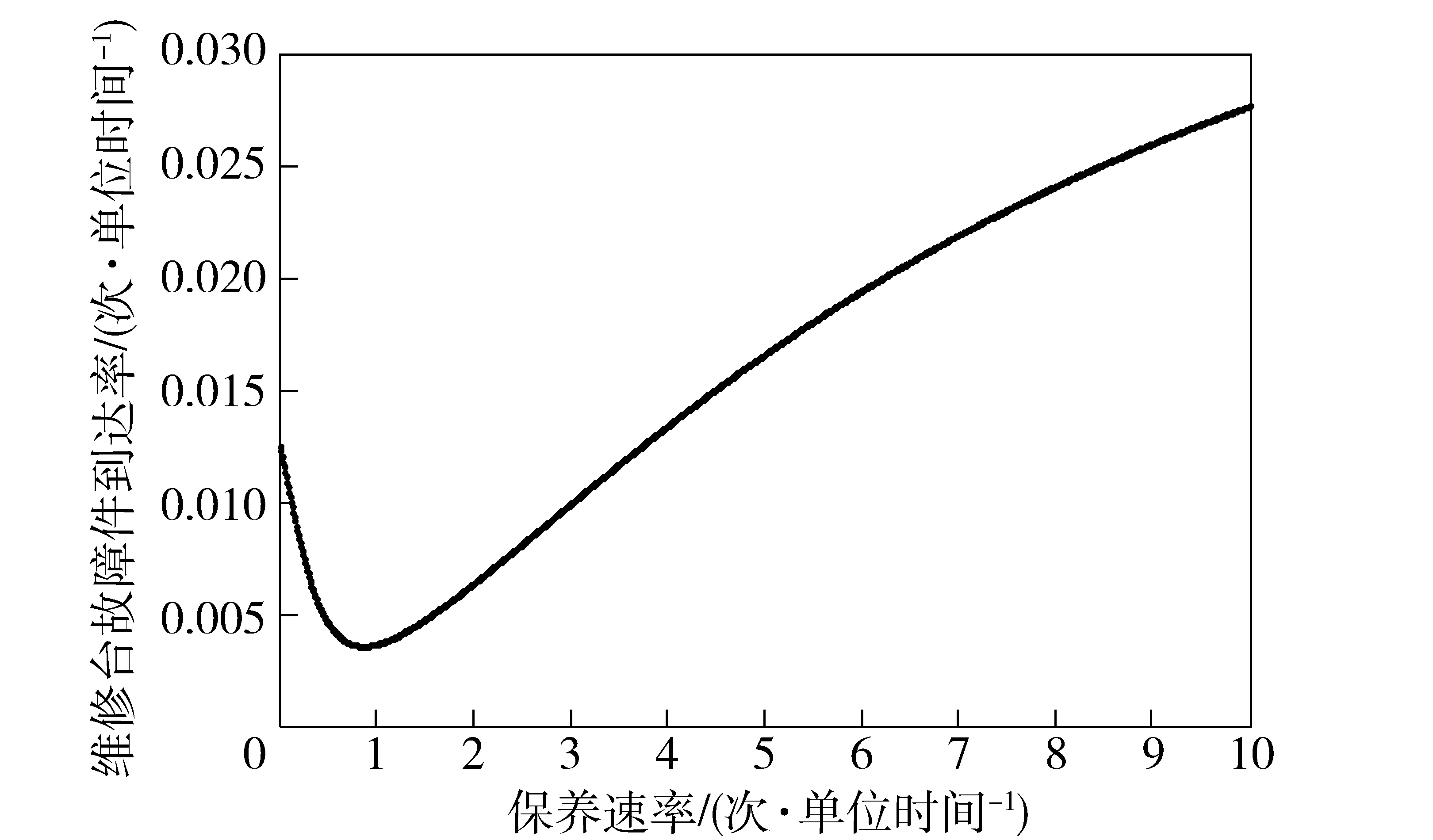
图3 保养速率对维修台故障件到达率的影响Fig.3 Relationship of preventive maintenance rate and failure arrival rate of repair facility

图4 保养速率对系统故障率的影响Fig.4 Relationship of preventive maintenance rate and system failure rate

由图1～图4可知，在该算例中保养速率过快或过慢并不利于提升系统可靠度，以及降低维修台故障到达率和系统故障率，而保养速率与系统平均停机间隔时间则具有近似线性关系。这是因为保养速率只会直接影响系统各部件在完好和一般状态的停留时间，不会直接影响系统的停机时间。因此，在实际的工程应用中，要注意选择合适的保养速率，使系统获得满意的可靠性指标。

同样，令维修时间也服从指数分布，可以方便地得出维修速率对系统可靠性的影响，如图5～图8所示。

图5 维修速率对可用度的影响Fig.5 Relationship of corrective maintenance rate and system stationary availability

图6 维修速率对系统平均停机间隔时间的影响Fig.6 Relationship of corrective maintenance rate and mean time between system halt

图7 维修速率对维修台故障件到达率的影响Fig.7 Relationship of corrective maintenance rate and failure arrival rate of repair facility

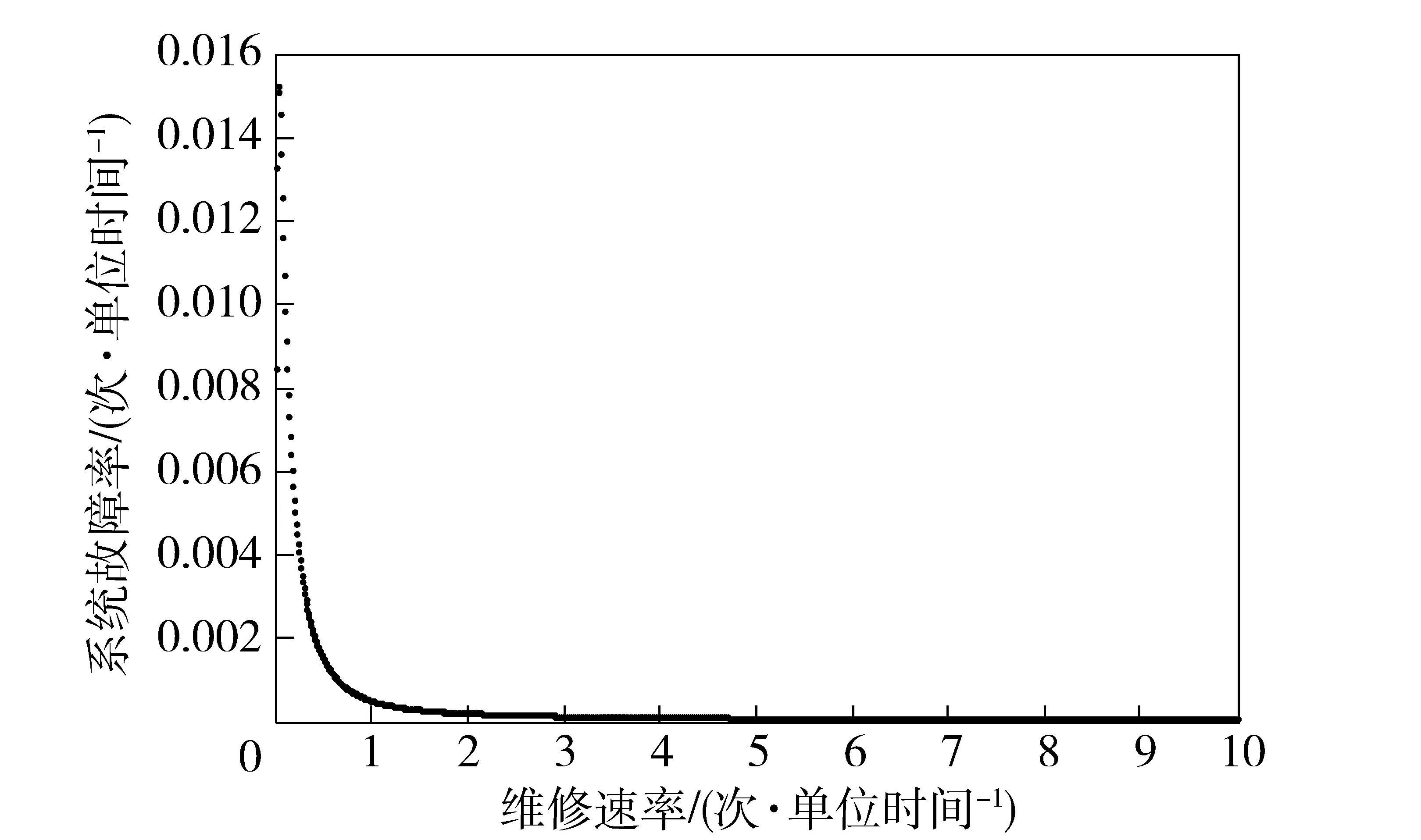
图8 维修速率对系统故障率的影响Fig.8 Relationship of corrective maintenance rate and system failure rate

由图5～图8可知，提升维修速率能够有效改善系统可靠性指标，但达到一定值后，其影响会越来越微弱。这是因为维修速率的小幅提升显然会有效缩短系统停机时间，并减少系统停机次数，从而提升系统平均停机间隔时间、降低系统故障率。当维修速率提升到一定程度时，维修活动对系统可靠性的影响已经趋于平稳，此时系统的可靠性指标主要还是取决于各部件自身的可靠性指标。

因此，在实际的工程实践中，需要合理配置维修资源，从而在获得满意的系统可靠性指标的同时，能够有效控制维修成本。

6 结论

本文针对大型装备系统存在不同优先级维修活动的现实，采用Phase-type分布研究了两部件多状态冷储备系统的可靠性规律，获得了系统稳态可用度、系统工作时间、系统平均停机间隔时间、维修台故障件到达率和系统故障率等参数的解析表达式，并通过算例分析了保养时间和维修时间对系统可靠性的影响。

研究结果表明，利用Phase-type分布表示各类随机时间分布，能够在确保模型良好解析特性的同时，有效提升模型的描述能力，也从模型假设条件环节保证了模型具有更强的通用性。同时，本文建立的模型在计算时主要涉及矩阵运算，目前高性能计算机和矩阵解析理论的应用能对大型矩阵的运算提供良好的支持。因此，在后续的研究工作中，可以尝试采用类似研究思路分析考虑维修优先权的复杂冗余系统可靠性问题。

References)

[1] Zio E. Reliability engineering: old problems and new challenges[J]. Reliability Engineering and System Safety, 2009, 94(2): 125-141.

[2] Gu Y K, Li J. Multi-state system reliability: a new and systematic review[J]. Procedia Engineering, 2012, 29(4): 531-536.

[3] Barton R M, Damon W W. Reliability in a multi-state system[C]∥6th Annual Southeastern Symposium on Systems Theory. Baton Rouge, Louisiana, US : IEEE, 1974.

[4] Lisnianski A, Frenkel I, Ding Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M]. London, UK: Springer, 2010.

[5] Zhang Y L,Wang G J. A deteriorating cold standby repairable system with priority in use[J]. European Journal of Operational Research, 2007, 183(1): 278-295.

[6] Zhang Y L,Wang G J. A geometric process repair model for a repairable cold standby system with priority in use and repair[J]. Reliability Engineering and System Safety, 2009, 94(11): 1782-1787.

[7] Leung K N F, Zhang Y L, Lai K K. Analysis for a two-dissimilar-component cold standby repairable system with repair priority[J]. Reliability Engineering and System Safety, 2011, 96(11): 1542-1551.

[8] Yuan L, Meng X Y. Reliability analysis of a warm standby repairable system with priority in use[J]. Applied Mathematical Modelling, 2011, 35(9): 4295-4303.

[9] Reetu, Malik S C. A parallel system with priority to preventive maintenance subject to maximum operation and repair times[J]. American Journal of Mathematics and Statistics, 2013, 3(6): 436-444.

[10] Kumara A, Malik S C. Reliability measures of a computer system with priority to PM over the H/W repair activities subject to MOT and MRT[J]. Management Science Letters, 2015, 5(1): 29-38.

[11] Moghaddass R, Zuo M J, Wang W B. Availability of a general k-out-of-n:G system with non-identical components considering shut-off rules using quasi-birth-death process[J]. Reliability Engineering and System Safety, 2011, 96(4): 489-496.

[12] Navarro J, Rubio R. Comparisons of coherent systems with non-identically distributed components[J]. Journal of Statistical Planning and Inference, 2012, 142(6): 1310-1319.

[13] He Q M. Fundamentals of matrix-analytic methods[M]. NY, US: Springer, 2013.

[14] Neuts M F, Meier K S. On the use of phase type distributions in reliability modelling of systems with two components[J]. OR Spektrum, 1981, 2(4): 227-234.

[15] Segovia M C, Labeau P E. Reliability of a multi-state system subject to shocks using phase-type distributions[J]. Applied Mathematical Modelling, 2013, 37(7): 4883-4904.

[16] Yu M, Tang Y, Liu L, et al. A phase-type geometric process repair model with spare device procurement and repairman’s multiple vacations[J]. European Journal of Operational Research, 2013, 225(2): 310-323.

[17] Montoro-Cazorla D, Pérez-Ocón R. A deteriorating two-system with two repair modes and sojourn times phase-type distributed[J]. Reliability Engineering and System Safety, 2006, 91(1): 1-9.

[18] 陈童, 黎放, 狄鹏. 基于PH分布的n中取k系统可靠性模型研究[J]. 系统工程理论与实践, 2015, 35(1): 260-266. CHEN Tong, LI Fang, DI Peng. The reliability analysis ofk-out-of-nsystem based on Phase-type distribution[J]. Systems Engineering-Theory & Practice, 2015, 35(1):260-266. ( in Chinese)

[19] 狄鹏, 黎放, 陈童. 考虑不同维修效果的多状态可修系统可靠性模型[J]. 兵工学报, 2014, 35(9):1488-1494. DI Peng, LI Fang, CHEN Tong, Reliability model of multi-state repairable systems with different repair effects[J]. Acta Armamentarii, 2014, 35(9):1488-1494.(in Chinese)

[20] LI Fang, YIN Dongliang, HU Bin. Analysis on reliability model for warm standby system with a repairman taking multiple vacations based on Phase-type distribution[C]∥Proceedings of IEEE International Conference on Industrial Engineering an Engineering Management. Bali, Indonesia: IEEE, 2016: 1436-1442.

[21] Kao E P C. An introduction to stochastic processes[M]. Beijing: China Machine Press, 2006.

[22] 田乃硕. 休假随机服务系统[M]. 北京: 北京大学出版社, 2001:5-7. TIAN Nai-shuo. Queuing systems with sever vacations[M]. Beijing:Peking University Press, 2001:5-7. (in Chinese)

Reliability Analysis of Multi-state Cold Standby System with Repair Priority

CHEN Tong, DI Peng, YIN Dong-liang

(Department of Management Engineering， Naval University of Engineering, Wuhan 430033, Hubei, China)

The maintenance mode of a multi-state cold standby system with two identical units is studied. According to the states of units, the single repair facility provides preventive maintenance and corrective maintenance, and the corrective maintenance has a higher priority. The residence time in the different performance levels of the operational unit, the preventive maintenance time and the corrective maintenance time are assumed to follow continuous Phase-type distribution, instead of exponential distribution or others typical distributions. The stationary distribution is built by using matrix analytic methods; and several performance measures of interest, such as the system stationary availability, operational time, mean time between system halt, failure arrival rate of repair facility and system failure rate, are obtained. Finally, the validity and applicability of the model are verified by numerical applications; and the influences of the preventive maintenance rate and the corrective maintenance rate on the system reliability measures are demonstrated. The study shows that the modeling of system reliability by Phase-type distribution can ensure the better analytical property of model, improve the description ability of model, and make the model have strong universality under the condition of some assumptions.

ordnance science and technology; multi-state; cold standby system; priority; reliability; Phase-type distribution

2016-11-15

国家自然科学基金项目(71501183)；海军工程大学自然科学基金项目(HGDQNJJ15033)

陈童(1980—)，男，讲师。E-mail: chentong@nudt.edu.cn

E92

A

1000-1093(2017)07-1422-08

10.3969/j.issn.1000-1093.2017.07.022