周期刺激作用下耦合神经振子集群的同步

赵小春, 焦贤发

(合肥工业大学 数学学院,安徽 合肥 230009)



周期刺激作用下耦合神经振子集群的同步

赵小春, 焦贤发

(合肥工业大学 数学学院,安徽 合肥 230009)

文章提出在外部周期刺激和噪声共同作用下全局耦合神经振子集群的相位演化模型，引入平均数密度描述神经振子集群的整体活动,利用Fokker-Planck方程导出了平均数密度的演化方程。数值模拟结果表明:刺激对神经振子群同步活动的影响取决于刺激强度和刺激频率;当刺激频率比系统特征频率小很多或者大得多时,神经振子集群的数密度呈现减幅振荡行为;当刺激频率接近系统特征频率时,神经振子集群趋于完全同步;在相同刺激频率条件下,神经振子集群的同步程度与刺激强度有关,刺激越强同步程度越高。

神经振子集群;周期刺激;噪声;平均数密度;同步振荡

神经元集群的振荡性同步放电行为广泛存在于哺乳动物的不同大脑皮层区域,大量的动物实验证明神经元集群的同步振荡活动是脑内神经信息处理的重要机制[1]。基于神经元集群的振荡性同步放电行为,使用全局耦合相位振子网络模型来研究神经系统的同步动力学行为是一种简单且有效的方法[2-5]。在医学、生物学、神经科学以及神经生理学等许多领域,神经振子集群的相位模型已被广泛研究[6-10]。用非线性Fokker-Planck方程描述随机动力系统状态概率密度的演化在很大程度上促进了对全局耦合相位振子集群的研究[4-6]。

真实的神经系统不可避免地要受到外部扰动或者其他神经振子集群的影响,探索神经系统对各种不同的外部信号的响应一直是计算神经科学领域的研究热点。神经系统的节律活动主要是由神经元之间的相互作用以及神经元与外部输入之间的相互作用产生的。神经系统许多功能的实现在很大程度上依赖于外部周期信号。例如,位于视交叉上核(suprachiasmatic nucleus，SCN)的大量神经元与昼夜循环周期的同步[10],不同的脑区与SCN节律的同步[11],以及心跳速率与窦房结(sinoatrial node，SAN)节律的同步[12]等。为了更清楚地了解这些系统的功能,过去的数十年间不断有研究者致力于研究神经动力系统对外部周期刺激或者来自其他脑区信号的响应。例如,用周期刺激模拟昼夜循环,可以使具有不同网络结构的耦合生物振子集群的频率达到一致[9];用一种线性化或圆极化电场代替SAN信号可以消除一些潜在的对生命有害的心律失常,从而恢复心肌细胞的相干跳动[13];文献[8,14]指出若对单个振子施加外部周期刺激,当振子的特征频率与信号频率接近时,就会出现锁相行为,并进一步证明了在耦合非线性振子网络中可以通过锁相行为检测到外部周期信号。然而,关于周期刺激如何影响神经系统的动力学行为方面的研究却很少。另外,神经系统中普遍存在的背景噪声也是不能忽略的,有研究表明噪声既有可能阻碍神经信息的处理和传递,也可能促进神经元集群的同步[15],考虑噪声的影响能够更真实地反映神经元集群的同步动力学行为。

综合考虑以上各方面的研究,本文建立外部周期刺激和噪声共同作用下全局耦合神经振子集群的相位演化模型,引入平均数密度来描述神经振子集群的同步模式。通过数值模拟研究自发活动情形下噪声强度对神经振子集群同步活动的影响,以及在刺激频率与系统特征频率的不同差值条件下,集群的同步发放模式以及刺激强度的变化对集群同步活动的影响。

1 数学模型

考虑外部周期刺激以及噪声共同作用下,N个全局耦合的神经振子集群的动力学演化方程为:

Isin(σt-θi)+ξi(t)

(1)

其中,i=1,…,N,N>1;θi为神经振子i的相位；Ω为单个神经振子的特征频率；K为弱耦合常数；I为刺激强度；σ为刺激频率；ξi(t)为作用于相位上与时间无关的随机噪声,为了计算方便将其模拟为零均值、δ相关的高斯白噪声,满足:

〈ξi(t)〉=0, 〈ξi(t)ξj(t′)〉=2Dδijδ(t-t′),

其中，D为噪声强度。

神经振子集群的动力学与外部周期刺激处于同一个旋转坐标系中[10],为此设ψi=θi-σt，则可将(1)式化为如下形式:

Isinψi+ξi(t)

(2)

其中,i=1,…,N。(2) 式的动力学可通过相应的Fokker-Planck方程来研究,即

(3)

其中,f为t时刻神经振子相位ψl落入区间(ψl,ψl+dψl)的概率密度,f=f({ψl};t),l=1,…,N。

定义具有相同相位ψ的神经元集群的数密度为:

(4)

考虑到神经系统的随机性,引入平均数密度为:

(5)

对平均数密度关于t求偏导得:

(6)

记

Γ(ψi,ψj)=(Ω-σ)+Ksin(ψj-ψi)-Isinψi

(7)

将(3)式代入(6)式,进行分部积分得:

(8)

(9)

将(7)式、(9)式代入(8)式得到平均数密度的演化方程为:

(10)

为得到偏微分方程(10)式的解,考虑以下2个边界条件对任意t成立,即

为了分析神经元集群的整体放电模式,考虑具有相同相位的神经元集群的数密度。若将神经元模拟成神经振子,则神经振子的相位ψ等于常数ψ0表示神经元发放1个动作电位。记p(t)=n(ψ0,t),则p(t)表示神经元集群在时刻t同时放电的神经元的密度[6],本文选取ψ0=0。

2 数值分析

当Ω=2π,D=0.4,K=0.1,σ=0,I=0时,在自发活动情形下,神经振子集群的放电模式表现为稳定的周期振荡,如图1所示。

图1 没有刺激条件下放电密度随时间的演化

当Ω=2π，K=0.1，σ=0，I=0时,在自发活动情形下,随着噪声强度的增大,神经振子集群的放电模式由稳定的周期振荡转变为减幅振荡行为,如图2所示。由图2可知,噪声强度越大振荡幅值越小,这表明噪声对神经振子群的振荡性同步活动有抑制作用。

为了研究外部周期刺激如何影响神经振子集群的活动,本文将神经系统的特征频率视为固定不变的常数,改变刺激频率的大小,观察不同的刺激频率与系统特征频率的大小关系下,神经振子集群的放电模式以及刺激强度的变化对集群同步活动的影响。

当Ω=2π,D=0.4,K=0.1,I=2.5时,不同的刺激频率条件下,神经振子集群的放电密度随时间的演化如图3所示。当刺激频率σ比神经系统的特征频率Ω小得多时,神经振子集群的同步活动受到抑制,呈现出减幅振荡行为;当σ接近Ω时,神经振子集群趋于完全同步;当σ大于Ω时,集群的同步受到抑制;随着σ的进一步增大,集群的放电密度再次呈现出减幅振荡行为,随着时间的增长,趋向于一个稳定的值。这表明当刺激频率与系统特征频率相差很多时,神经振子集群的节律性同步放电会受到抑制,当刺激频率接近系统特征频率时,神经系统接近完全同步。

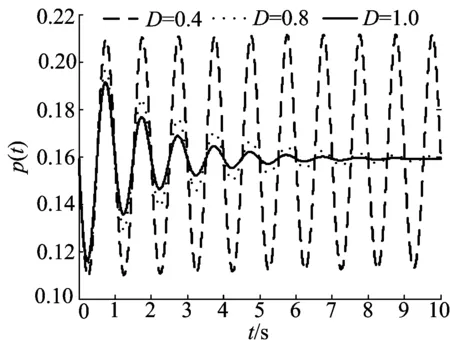
图2 不同噪声强度下放电密度随时间的演化

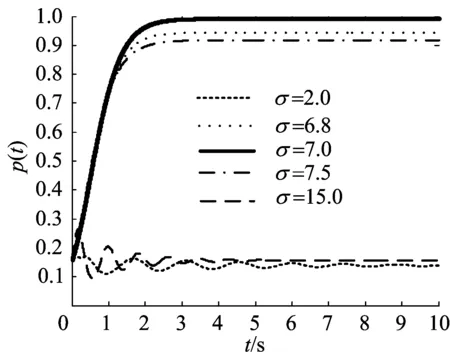
图3 不同刺激频率下放电密度随时间的演化

当Ω=2π,D=0.4,K=0.1时,相同刺激频率条件下,刺激强度的变化对神经元集群同步活动的影响如图4所示。当刺激频率σ比系统特征频率Ω小很多时,弱刺激条件下,神经元集群的放电密度只能产生微弱的减幅振荡,然后趋向于平稳,刺激强度越大,就越快地趋于平稳;当刺激强度增大到一定值时,神经元集群将迅速地达到完全同步而后又迅速失去同步最后趋于平稳(图4a),这表明低频刺激下,刺激强度可以改变集群的同步放电模式,弱刺激会抑制神经系统的节律性同步活动,强刺激使神经元集群迅速达到完全同步而后趋于平稳。当刺激频率σ接近系统特征频率Ω时,弱刺激条件下,神经振子集群的相位同步程度很低;然而随着刺激强度的增加,集群的同步程度将逐渐增大,并且更快地趋于同步(图4b),这表明当刺激频率σ接近系统特征频率Ω时,刺激强度由集群的相位同步程度编码。

图4 不同刺激强度下放电密度随时间的演化

3 结 论

文献[10]研究了周期刺激作用下耦合振子群的相位模型,给出了系统各种不同的行为相互转化的分岔分析。本文在文献[10]模型的基础上,考虑噪声环境下周期刺激对全局耦合神经振子集群同步模式的影响,通过数值模拟具体分析了耦合神经振子群的同步动力学行为。

数值模拟结果表明在自发活动情形下,神经振子集群的放电模式表现为稳定的周期振荡;同时噪声强度的增大会抑制神经振子集群的振荡性同步活动。在适当强度的刺激下,当刺激频率与系统特征频率差别很大时,集群的数密度呈现出减幅振荡行为;当刺激频率接近系统特征频率时,神经振子集群趋于完全同步。当刺激频率比集群特征频率小很多时,弱刺激只能使神经振子集群产生微弱的同步响应;强刺激可以使集群快速达到完全同步,然后失去同步,最后趋于平稳状态。当刺激频率接近神经振子集群的特征频率时,刺激强度由集群的相位同步程度编码,刺激越强同步程度越高。

[1] GRAY C M，SINGER W.Stimulus-specific neuronal oscillation in orientation columns of cat visual cortex[J].Process of the National Academy of Science，1989，86:1698-1702.

[2] KURAMOTO Y.Collective synchronization of pulse-coupled oscillators and excitable units[J].Physica D:Nonlinear Phenomena，1991,50(1):15-30.

[3] BAIBOLATOV Y，ROSENBULM M，ZHANABAEV Z Z，et al.Periodically forced ensemble of nonlinearly coupled oscillators:from partial to full synchrony[J].Physical Review E，2009，80:046211-1-046211-12.

[4] BREAKSPEAR M，HEITMANN S，DAFFERTSHOFER A.General models of cortical oscillations: neurobiological implications of the Kuramoto model[J].Frontiers in Human Neuroscience，2010，190(4):1-14.

[5] 黄小娟，焦贤发，周堂春.一类非线性时滞Fokker-Planck方程的近似平稳解[J].合肥工业大学学报(自然科学版)，2008，31(11):1886-1889,1893.

[6] TASS P A.Phase resetting in medicine and biology[M].Berlin: Springer-Verlag，1999: 98-106.

[7] WANG Rubin，JIAO Xianfa.Stochastic model and neural coding of large-scale neuronal population with variable coupling strength[J].Neurocomputing，2006，69:778-785.

[8] PIKOVSKY A，ROSENBULM M.Dynamics of globally coupled oscillators: progress and perspectives[J].Nonlinear Sciences，2015,1504:1-25.[9] ANTONSEN T M，FAGHIH R T，GIRVAN M et al.External periodic driving of large systems of globally coupled phase oscillators[J].Chaos，2008，18(3):037112.

[10] CHILDS L M，STROGATZ S H.Stability diagram for the forced Kuramoto model[J].Chaos，2008,18(4):043128.

[11] YAMAGUCHI S，ISEJIMA H，MATSUO T，et al.Synchronization of celluar clocks in the suprachiasmatic nucleus[J].Science，2003，302:1408-1412.

[12] GLASS L，MANKEY M C.From clocks to chaos:the rhythms of life[M].Princeton:Princeton University Press，1988:3-16.

[13] LUTHER S FENTON F H，KORNREICH B G，et al.Low-energy control of electrical turbulence in the heart[J].Nature，2011，475:235-239.

[14] LIU Zonghua.Organization network enhanced detection and transmission of phase-locking[J].A Letters Journal Exploring the Frontiers of Physics，2012，100:60002.

[15] ERMENTROUT G B，GALAN R F，URBAN N N.Reliability，synchrony and noise[J].Trends in Neurosciences,2008,31:428-434.

(责任编辑 张淑艳)

Synchronization of coupled neuronal oscillator population under external periodic driving

ZHAO Xiaochun, JIAO Xianfa

(School of Mathematics， Hefei University of Technology， Hefei 230009， China)

A phase model of globally coupled neuronal oscillator population in the presence of external periodic stimulus and noise is proposed， and the evolution equation of average number density describing the overall activity of neuronal population is derived with the Fokker-Planck equation. The results of numerical simulations indicate that the impact of stimulus on synchronization of a population of neuronal oscillators depends on stimulation intensity and stimulation frequency. If the stimulus frequency is much smaller or larger than the characteristic frequency of system， the number density of neuronal population shows a damped oscillation behavior. If the stimulus frequency is close to the characteristic frequency of system， the neuronal population tends to complete synchronization. As the stimulus frequency is fixed， stimulus with stronger intensity leads to higher synchronization.

neuronal oscillator population; periodic stimulus; noise; average number density; synchronous oscillation

2016-04-01；

2016-06-02

国家自然科学基金资助项目(11172086;11232005);安徽省省级质量工程专业综合改革试点资助项目(2012zy007)和名师(大师)工作室资助项目(2015msgzs126)

赵小春(1992-),女,安徽阜阳人,合肥工业大学硕士生; 焦贤发(1965-),男,安徽安庆人,博士，合肥工业大学教授,硕士生导师,通讯作者,E-mail:xfjiao@126.com.

10.3969/j.issn.1003-5060.2017.07.026

O29

A

1003-5060(2017)07-1000-04