内置钢骨GFRP管混凝土中长柱偏压承载力分析

张海霞, 刘 鹤, 孙云杰

(沈阳建筑大学 土木工程学院,辽宁 沈阳 110168)



内置钢骨GFRP管混凝土中长柱偏压承载力分析

张海霞, 刘 鹤, 孙云杰

(沈阳建筑大学 土木工程学院,辽宁 沈阳 110168)

为了提出内置钢骨玻璃纤维增强复合材料(glass fiber reinforced polymer,GFRP)管混凝土中长柱的偏压承载力计算方法,文章通过对7根内置钢骨GFRP管混凝土中长柱进行偏压试验,分析了长细比、偏心距、混凝土强度对组合柱偏压性能的影响,建立了考虑偏心距影响的承载力折减系数计算公式。利用ABAQUS有限元分析软件,对组合柱轴压性能进行数值模拟,在验证有限元分析结果正确的基础上,确定了短柱与中长柱长细比的界限值以及组合柱弹性失稳长细比的界限值,推导了考虑长细比影响的承载力折减系数计算公式,建立了组合柱偏压承载力实用计算公式,并将理论值与试验值进行了对比。结果表明,组合柱的偏压承载力随着长细比和偏心距的增大而减小,建立的偏压承载力计算公式理论值与试验值吻合良好。

内置钢骨;GFRP管混凝土;中长柱;长细比和偏心距影响;偏压承载力

内置钢骨玻璃纤维增强复合材料(glass fiber reinforced polymer,GFRP)管混凝土组合柱是由GFRP管、钢骨、核心混凝土3个部分构成的,即在GFRP 管混凝土柱内埋置钢骨的组合构件。该构件的各个组成部分之间具有良好的协同工作性能,这使得其表现出较好的力学性能:① GFRP管对混凝土提供环向约束作用,使混凝土处于三向受力状态,其强度得到提高,塑性得到改善[1-7];② 内置钢骨不仅可以提高构件的承载能力,而且可以增大构件的延性性能;③ 混凝土的存在可以避免或延缓GFRP管过早地发生局部破坏,保证材料性能得到充分发挥;④ GFRP管还可以作为浇筑其核心混凝土的模板,可加快施工速度。文献[8-9]对GFRP管钢骨高强混凝土组合柱进行了轴心受压和偏压试验研究;文献[10]分析了构件的工作机理和破坏模式,建立了组合柱极限承载力简化计算公式;文献[11]进行了纤维增强复合材料(fibre-reinforced polymer,FRP)纤维缠绕角度对组合柱偏压力学性能的影响分析。然而,这些研究成果还需要做进一步的验证。基于此,本文重点考虑长细比和偏心矩2个影响组合柱偏心力学性能的主要因素,在试验研究和有限元分析的基础上,确定了组合短柱和中长柱长细比的界限值和组合柱弹性失稳时长细比的界限值,推导了考虑长细比和偏心距影响的承载力折减系数计算公式,并利用经验系数法,进一步建立了内置钢骨GFRP管混凝土中长柱的偏压承载力计算公式,为工程应用奠定良好的理论基础。

1 试验研究

1.1 试验概况

本次试验设计了7个内置钢骨的GFRP管混凝土试件,其截面如图1所示。

图1 试件截面

试件混凝土设计强度等级为C30和C50,通过对150 mm×150 mm×150 mm混凝土立方体试块抗压强度值测定,其抗压强度分别为44.1、56.2 MPa。试件所用GFRP管内径为190 mm,壁厚为5 mm,GFRP纤维缠绕角度为80°,其环向抗拉强度为340 MPa,环向弹性模量为13.42 GPa。钢骨采用Q235B的I10工字钢,横截面积为14.33 cm2,实测屈服强度为290.2 MPa。试件2个主要参数为偏心距e和长细比λ,设计e为20、40、80 mm,λ为20、24、32,试件的主要参数见表1所列。表1中,L为柱长;Ne,u为极限承载力试验值;Ncal,u为极限承载力计算值。

表1 试件参数及试验结果

试验在5 000 kN压力机上进行,对试件进行一次性单向偏压试验。加载方向为强轴加载,即加载线与工字钢腹板垂直。试件两端为铰接,通过刀口铰加载,偏压柱形心线与刀口铰中心线的距离为偏心距。试件同时作用轴向压力N和弯矩M,两者按比例同步增大。试验采用分级加载制度,在达到预估极限荷载70%以前,每级荷载为极限荷载的1/15;在达到预估极限荷载70%以后,缓慢加载以观察试件变形情况,此时每级荷载为极限荷载的1/25。当试件的GFRP管被拉断、试件侧向挠度过大或荷载值降到极限荷载75%以后,停止试验。组合柱位移测量主要是侧向挠度,沿柱长四分点处布置量程为10 cm的位移计。应变测量主要是型钢和FRP管的应变,试验加载装置及位移测点布置分别如图2、图3所示。

图2 加载装置及位移测点

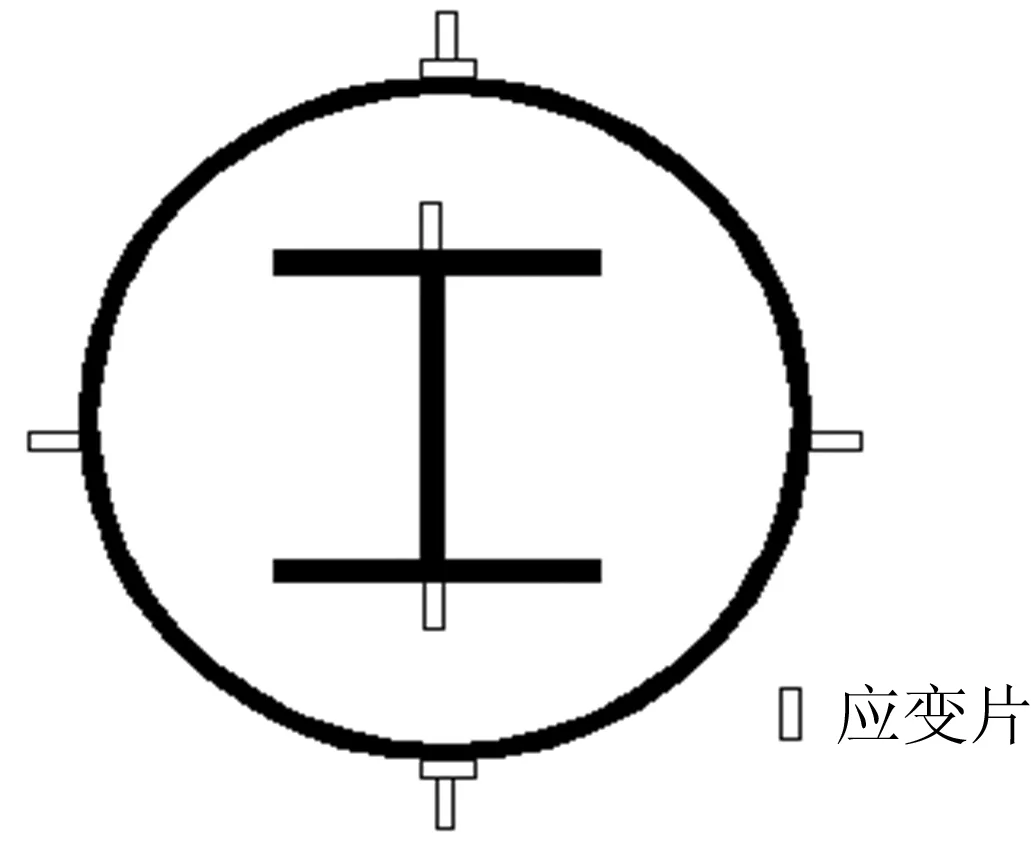
图3 应变片测点布置

1.2 试验破坏现象

典型试件破坏形态如图4所示。

选取偏心距较小的典型试件L10-E20-P进行分析。在荷载加载初期,试件变形增长缓慢;当达到极限荷载85%时,GFRP管外表面出现白纹,并伴有轻微的纤维拉断声;随着荷载的持续增大,纤维拉断声逐渐增多、增大,试件GFRP管外表面白纹愈加明显;达到极限荷载后,试件变形明显,侧向挠度也逐渐增大;在加载末期,纤维断裂声更加频繁,柱中截面位置处的GFRP管受拉区出现横向裂纹,受压区出现沿管长度方向的纵向裂纹并有轻微褶皱出现;最后,随着一声巨大的声响,GFRP管受压区纤维沿管长度方向被压溃,受压区混凝土被压碎,试件退出工作。而偏心距较大的试件L10-E80-P破坏时,GFRP管表面有白纹,但GFRP纤维受拉区未见明显裂纹,受压区沿GFRP管长度方向出现轻微横向褶皱,试件最终因侧向挠度过大而停止加载。而长细比较大的典型试件L16-E40-P破坏时,GFRP管受拉区未见裂纹出现,受压区出现横向褶皱,试件最终因荷载值下降过快且降为极限荷载75%后而停止加载。

从试验现象可以看出,内置钢骨的GFRP管混凝土中长柱在偏压荷载作用下,变形明显,破坏时有明显征兆,极限荷载以后承载力缓慢下降,表现出较好的延性性能。为了观察试件混凝土的破坏形态,选取典型破坏试件L10-E40-P进行剖解,将部分GFRP管移除,GFRP管混凝土受拉区和受压区破坏形态如图4d所示。

图4 典型试件破坏形态

可以看出,GFRP管受拉区柱中截面白纹较多、有明显的横向裂纹,此位置处对应的混凝土也出现横向裂缝,且此处的裂缝宽度最大,GFRP管受拉区柱中部截面两侧白纹较少、未见明显的横向裂纹,此位置处混凝土出现分层的横向裂纹,数量较多但宽度较小;受压区柱中部截面GFRP管沿纵向被拉断并出现沿柱长方向的褶皱,此位置处对应的混凝土出现大面积压碎,可轻易剥落。从GFRP管和混凝土的破坏形态及破坏位置可以看出,两者表现出良好的黏结性能,可以共同工作。

1.3 长细比、偏心矩及混凝土强度的影响

由表1可知,试件L10-E40-P、L12-E40-P和L16-E40-P在混凝土强度、偏心距均相同的情况下,长细比不同时试件偏压承载力分别为1 119、1 046、849 kN。随着长细比的增大,试件的偏压承载力逐渐降低,试件L16-E40-P的偏压承载力比试件L10-E40-P和L12-E40-P分别降低了24.13%和18.83%。

试件L10-E20-P、L10-E40-P和L10-E80-P在混凝土强度、长细比相同情况下,偏心距不同时试件的偏压承载力分别为1 553、1 119、575 kN。试件L10-E80-P的极限承载力比试件L10-E20-P和L10-E40-P分别降低了63%和48.6%。由于偏心距的增大,GFRP管对试件的环向约束作用降低,使得试件的偏压承载力逐渐降低。

另外,在偏心距、长细比相同的情况下,试件的极限承载力随着混凝土强度的增大而增加;试件L10-E20-G的极限承载力比L10-E20-P提高了21.5%,试件L10-E40-G的极限承载力比L10-E40-P提高了13.1%,偏心距的增大降低了混凝土强度对试件极限承载力的影响,偏心距较大时试件极限承载力提高幅度小。出现这种情况的原因主要有2个:① 随着混凝土强度的提高,混凝土变形能力减弱,使得GFRP管对混凝土的约束作用降低; ② 偏心距的增大减小了GFRP管对试件的约束作用。

2 有限元分析

本文利用ABAQUS有限元软件,建立组合中长柱轴压有限元模型,通过分析长细比的影响,确定界限长细比,以便建立考虑长细比影响的组合柱偏压承载力计算公式。

2.1 有限元模型的验证

本文通过对GFRP管、混凝土、钢骨材料力学参数进行合理简化后,在ABAQUS中建立内置钢骨的GFRP管混凝土中长柱偏压力学模型。为了验证有限元模拟结果的正确性,将典型试件荷载-挠度曲线与试验结果进行对比,如图5所示。

由图5可见,有限元模拟的结果与试验结果吻合较好,说明建立的有限元模型可以真实、有效地模拟内置钢骨的GFRP管混凝土中长柱的受力性能。

图5 荷载-挠度曲线对比

2.2 长细比界限值

试件的材料参数选取依据本文试验所获得的数据,长细比为主要参数,变化范围为12～92,有限元分析计算结果见表2所列。

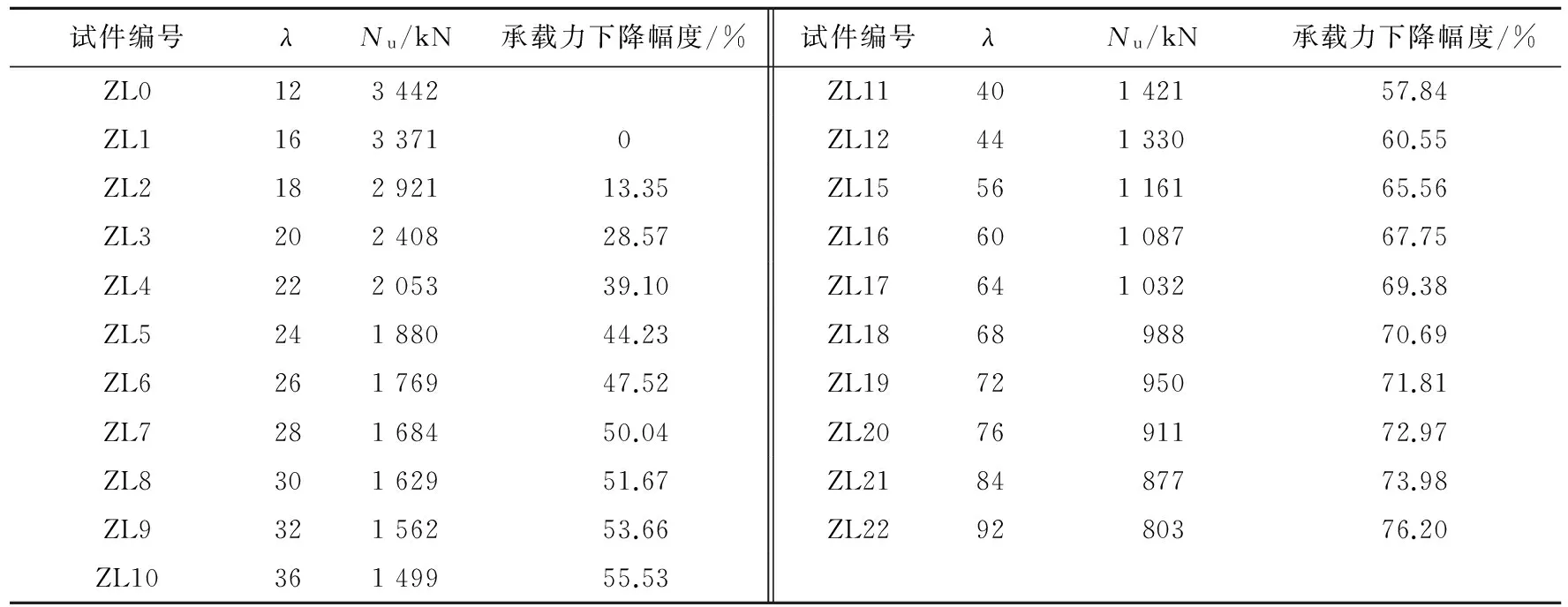
表2 组合柱数值模拟结果

注:承载力下降幅度是指λ>16的构件与λ=16的构件相比,其承载力下降的程度。

内置钢骨的GFRP管混凝土组合柱轴心受压的力学性能与钢筋混凝土柱相比要复杂得多。对于长细比较小的短柱,其破坏是材料达到极限强度导致的;对于长细比较大的长柱,其破坏是由于发生了弹性失稳所致,此时的纵向应变处于弹性范围之内;而长柱与短柱之间存在范围较大的中等长细比的中长柱,其破坏可能是发生了非弹性失稳破坏。为此,将内置钢骨的GFRP管混凝土短柱与中长柱长细比的界限值定义为λl,中长柱与长柱长细比的界限值定义为λp,即λp为发生弹性失稳的界限长细比。不同长细比下组合柱的轴向荷载(N)-轴向平均应变(ε)关系曲线如图6所示。

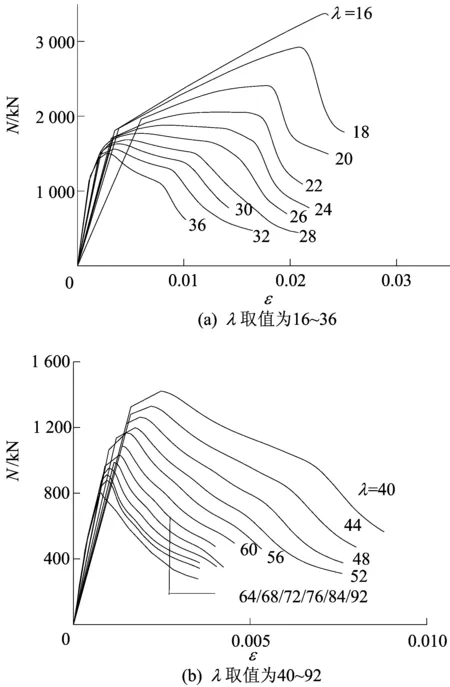
图6 组合柱N-ε关系曲线

从表2和图6中可以看出,随着长细比λ的增大,构件的极限承载力逐渐下降,破坏状态由强度破坏逐渐转变为失稳破坏。当λ≤16时,λ对构件的极限承载力影响很小,因而定义λl=16为短柱与中长柱的界限值。当18≤λ≤22时,构件的破坏以强度破坏为主;当长细比24≤λ≤92时,构件的破坏主要表现为失稳破坏,其中24≤λ≤84时,N-ε关系曲线在弹塑性阶段达到极限承载力;λ=92时,N-ε关系曲线在弹性阶段达到极限承载力,因此,定义该组合柱弹性失稳的长细比界限值λp=92。

3 中长柱偏压承载力的计算

本文参照文献[12]中单肢柱承载力计算公式,确定内置钢骨的GFRP管混凝土中长柱的偏压承载力计算公式为:

Nu=φlφeN0

(1)

其中,Nu为中长柱偏压承载力;φl为考虑长细比影响的承载力折减系数;φe为考虑偏心距影响的承载力折减系数;N0为内置钢骨GFRP管混凝土短柱轴压承载力,采用文献[13]给出的计算公式。

3.1 φl的计算表达式

对于内置钢骨的GFRP管混凝土中长柱轴压构件,在初始偏心距的影响下,受力初期便产生侧向挠度,二阶效应的影响又使得构件产生附加弯矩,而附加弯矩作用又导致构件侧向挠度增大,如此循环,最终导致构件发生破坏[14]。从大量有限元分析结果可知,构件的极限承载力随着长细比的增大而降低,但降低幅度逐渐减缓,出现这种情况的原因主要是由于长细比的增大导致构件极限承载力降低，同时也使得初始偏心距对构件力学性能的影响降低,长细比成为影响构件极限承载力的主要因素,构件的极限承载力降低趋势变缓,破坏形态逐渐由材料强度破坏向失稳破坏过渡。考虑长细比的影响,仿照钢管混凝土轴压中长柱长细比折减系数的计算方法,通过大量的有限元分析,将计算结果进行数据回归,得到φl的计算表达式为：

(2)

(3)

其中,L为柱子的计算长度;D为柱子直径;ζ为长细比影响系数;λ为柱子的长细比;e0为偏压柱的初始偏心距。

3.2 φe的计算表达式

根据极限平衡理论,偏压柱在柱端弯矩M和轴向力N的作用下,其广义屈服条件在直角坐标系中为一条外凸的曲线。与任何稳定材料的偏压构件一样,对于内置钢骨GFRP管混凝土中长柱在偏心距较小时,可以用一条直线简化表示外凸的屈服曲线[15],该直线表达式为:

(4)

其中,N0、M0分别为偏压柱所受的轴向力和弯矩;Nu、Mu分别为偏压柱的极限轴力和极限弯矩;a为待定系数。

内置钢骨GFRP管混凝土纯弯构件的极限弯矩[15]可表达为：

M0=N0rcb

(5)

其中,rc为核心混凝土的半径;b为小于1的系数。

Mu可表达为:

Mu=Nue0

(6)

将(5)式和(6)式代入(4)式中可得:

(7)

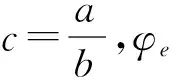
(8)

即φe与e0/rc之间的关系为一条双曲线。本文通过对试验数据进行回归,得到c的表达式为:

(9)

为了验证本文建立的内置钢骨GFRP管混凝土中长柱偏压承载力计算公式的正确性,将(4) 式的计算结果与试验结果进行对比,见表1所列。由表1可见,理论计算结果与试验结果比值的平均值为1.044,均方差为0.039 4,两者吻合较好。

4 结 论

(1) 长细比和偏心距是影响内置钢骨GFRP管混凝土中长柱承载力的主要因素。随着长细比和偏心矩的增大,组合柱的承载力逐渐降低。

(2) 基于大量的有限元数据回归,建立了考虑长细比影响的承载力折减系数φl的计算表达式。

(3) 基于有限元分析,确定了短柱与中长柱长细比界限值和弹性失稳时的长细比界限值,进一步建立了考虑偏心距影响的承载力折减系数φe的计算表达式。

(4) 采用经验系数法,建立了组合柱偏心受压承载力计算公式,并将理论计算结果与试验结果进行了对比,两者吻合较好,但其实用性和通用性仍需要更多的试验加以验证。

[1] MIRMIRAN A,SHAHAWY M,SAMAAN M,et al.Effect of column parameters on FRP-confined concrete [J].Journal of Composites for Construction,1998,2(4):175-185.

[2] 吴刚,吕志涛.FRP约束混凝土圆柱无软化段时的应力-应变关系研究[J].建筑结构学报,2003,24(5):1-9.

[3] MIRMIRAN A,SHAHAWY M,EL-KHOURY C,et al.Large beam-column tests on concrete-filled composite tubes [J].ACI Structural Journal,2000,97(2):268-276.

[4] FAM A,RIZKALLA S.Large scale testing and analysis of hybrid concrete composite tubes for circular beam-column applications [J].Construction and Building Materials,2003,17(6/7):507-516.

[5] 李杰,薛元德,李文晓.GFRP管混凝土组合结构压弯构件非线性全过程分析[J].玻璃钢/复合材料,2006 (3):7-10.

[6] 李杰,薛元德.FRP管混凝土组合结构试验研究[J].玻璃钢/复合材料,2004(6):7-10.

[7] COLE B,FAM A.Flexural load testing of concrete-filled FRP tubes with longitudinal steel and FRP rebar [J].Journal of Composites for Construction,2006,10(2):161-171.

[8] 王连广,秦国鹏,周乐.GFRP管钢骨高强混凝土组合柱轴心受压试验研究[J].工程力学,2009,26(9):170-175,185.

[9] 王连广,周乐.GFRP管钢骨高强混凝土偏压柱试验研究[J].工程力学,2011,28(1):145-149,156.

[10] 秦国鹏,王连广,刘美思.GFRP管钢骨混凝土组合柱偏压承载力计算[J].东北大学学报(自然科学版),2010,31(8):1200-1203.

[11] 张海霞,何禄源,曹朋朋.FRP纤维缠绕角度对FRP管约束钢骨混凝土中长柱偏压力学性能的影响分析[J].建筑结构学报,2013,34(增刊1):345-352.

[12] 哈尔滨工业大学,中国建筑科学研究院.钢管混凝土结构设计技术规程:CECS28:2012[S].北京:中国计划出版社,2012:19-23.

[13] 陈百玲,秦国鹏,王连广.GFRP管钢骨混凝土轴压短柱承载力研究[J].东北大学学报(自然科学版),2010,31(7):1035-1038.

[14] 关宏波.GFRP套管钢筋混凝土组合结构的研究[D].大连:大连理工大学,2011.

[15] 蔡绍怀.现代钢管混凝土结构[M].北京:人民交通出版社,2003:142-143.

(责任编辑 张淑艳)

Analysis of bearing capacity of steel-encased concrete filled GFRP tubes middle-long column subjected to eccentric compression load

ZHANG Haixia, LIU He, SUN Yunjie

(School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China)

The experiment of seven steel-encased concrete filled glass fiber reinforced polymer(GFRP) tubes column subjected to eccentric compression load is presented to explore the computation method of the composite column. The effect of slenderness ratio, eccentricity and strength of concrete on the behavior of the composite under eccentric compression is analyzed. The calculating formula of reduction coefficient of bearing capacity considering the influence of eccentricity is established. The numerical simulation on the composite column under axial compression is conducted through the finite element analysis software ABAQUS. Based on the verified validity of simulation results against experimental results, the boundary values of the short column to middle-long column and the slenderness ratio under elastic buckling of the composite column are determined, and the calculating formula of reduction coefficient of bearing capacity considering the influence of slenderness ratio is deduced. Furthermore, the practical calculation formula of the bearing capacity of the composite column subjected to the eccentric compression load is established, whose values are compared with the test results. The results indicate that the bearing capacity of the composite column decreases with the increase of eccentricity and slenderness ratio. The theoretical results from the calculation formula have a good agreement with test results.

steel-encased; concrete filled glass fiber reinforced polymer(GFRP) tube; middle-long column; effect of slenderness ratio and eccentricity; bearing capacity under eccentric compression load

2015-10-15；

2017-04-21

辽宁省自然科学基金资助项目(20170540750);辽宁省高等学校优秀科技人才支持计划资助项目(LR2015055)和沈阳建筑大学学科涵育计划资助项目(XKHY2-15)

张海霞(1976-),女,辽宁沈阳人,博士,沈阳建筑大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.07.020

TU398.9

A

1003-5060(2017)07-0965-06