椭圆钢管混凝土受扭性能及抗扭承载力计算

宋顺龙, 王静峰, 江 汉, 沈奇罕

(1.中交铁道设计研究总院有限公司,北京 100097; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)



椭圆钢管混凝土受扭性能及抗扭承载力计算

宋顺龙1, 王静峰2, 江 汉2, 沈奇罕2

(1.中交铁道设计研究总院有限公司,北京 100097; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

为研究椭圆钢管混凝土构件的受扭性能和抗扭承载力计算,文章通过ABAQUS建立了椭圆钢管混凝土受扭构件的理论分析模型,开展了椭圆钢管混凝土构件受扭性能的参数分析,研究参数包括钢材强度、混凝土强度、截面含钢率、截面面积和长短轴比,揭示了椭圆钢管混凝土构件在纯扭状态下的受力机理,提出了椭圆钢管混凝土纯扭构件的抗扭承载力简化计算公式。研究结果表明:椭圆钢管混凝土构件的抗扭强度承载力随着钢材强度、截面面积和含钢率的增大而增大;椭圆钢管混凝土构件的扭矩(T)-转角(θ)曲线可分为弹性阶段、弹塑性阶段和塑性强化阶段,表现出良好的塑性性能;提出的椭圆钢管混凝土构件抗扭强度承载力公式可用于椭圆钢管混凝土设计中。

椭圆钢管混凝土构件;有限元;受扭性能;抗扭承载力;受力机理

椭圆钢管混凝土构件是一种新型截面形式,具有圆、方形钢管混凝土的优点,还具有特有的建筑美学效果,其长短轴能提供不同的抗侧刚度,且受风流体阻力系数小,在马德里机场、伦敦Heathrow机场5号航站楼及爱尔兰柏林机场航站楼等有所应用,有望在高架桥梁、空间管桁架、办公楼等工程中推广和应用。然而我国缺乏此类结构应用。

目前国内外相关研究都是对椭圆钢管混凝土柱的轴压、偏压和受弯性能的试验研究和数值分析。例如,文献[1]对21个椭圆钢管混凝土试件进行轴压试验,研究了钢管壁厚、混凝土等级和混凝土收缩等参数影响;文献[2]开展了轴压下椭圆钢管混凝土长柱的数值模拟与试验分析;文献[3]通过试验分析钢管厚度和偏心距对椭圆钢管混凝土柱偏心受压性能的影响。文献[4-5]通过理论和试验分析进行了椭圆钢管混凝土轴压短柱、长柱和抗弯的研究;文献[6]进行了椭圆钢管混凝土柱轴压、压弯和纯弯试验研究,考虑了荷载偏心距、柱长细比、剪跨比、截面类型的影响。然而,在实际工程中椭圆钢管混凝土构件可能会承受较大的扭转作用,例如，建筑物的框架角柱、螺旋楼梯的中心柱等。因此,有必要研究椭圆钢管混凝土构件的受扭问题。

本文通过有限元软件ABAQUS,建立纯扭矩作用下椭圆钢管混凝土构件的有限元分析模型,系统分析了混凝土强度、钢材强度、径厚比、长短轴比等参数对其受扭性能的影响,探讨椭圆钢管混凝土构件在受扭状态下的破坏形态,并提出了抗扭承载力建议公式。

椭圆钢管混凝土截面形式如图1所示。

图1 椭圆钢管混凝土截面形式

1 理论分析模型与试验验证

本文采用有限元软件ABAQUS对椭圆钢管混凝土纯扭构件进行了分析,包括材料本构关系选择、单元选取、网格划分、边界条件与接触条件的确定等。

1.1 材料模型

钢材的本构关系模型采用二次流塑性模型[7],其应力-应变关系曲线如图2所示。

对于椭圆钢管混凝土受扭构件的核心混凝土本构关系,本文先将椭圆形核心混凝土直径等效为圆形核心混凝土直径De[8],再采用文献[9]提出的混凝土应力-应变关系模型。

图2 钢材的应力(σ)-应变(ε)关系曲线

具体公式如下:

(1)

(2)

(3)

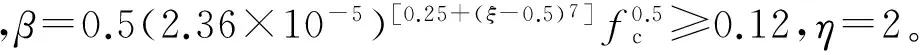
1.2 有限元模型

有限元模型由上下盖板、钢管及核心混凝土组成。混凝土、钢管和上下盖板均采用八节点减缩积分格式C3D8R三维实体单元来模拟。考虑了钢管与混凝土之间相对滑移,相互作用采用“表面与表面接触”,法向行为定义为“硬接触”,切向行为采用类型为“罚”。 椭圆钢管混凝土纯扭构件的有限元分析模型如图3所示。

图3 有限元分析模型

混凝土和钢管与盖板之间采用绑定约束,在盖板上施加转角位移以实现扭矩。施加转角位移端的盖板没有边界约束,而在另一端施加固定边界条件。

1.3 试验验证

目前国内外还没有椭圆钢管混凝土构件的扭转试验研究,可根据现有圆、方钢管混凝土扭转试验数据和椭圆钢管混凝土轴压、偏压试验数据来验证椭圆钢管混凝土扭转有限元分析模型。因此本文先将文献[10-14]中圆、方形钢管混凝土构件扭转试验的试验结果分别与本文的有限元模型分析结果进行比较,对比结果见表1所列,如图4所示。表1中D为圆管直径或方管边长,t为管壁壁厚,L为试件长度,单位为mm;fy为钢材屈服强度;fcu为混凝土立方体抗压强度Tue为试件抗扭强度试验值;Tuc为试件抗扭强度计算值。

表1 有限元计算结果与相关试验结果比较

注:试件S-T和试件FC为方形截面,其余为圆形截面。

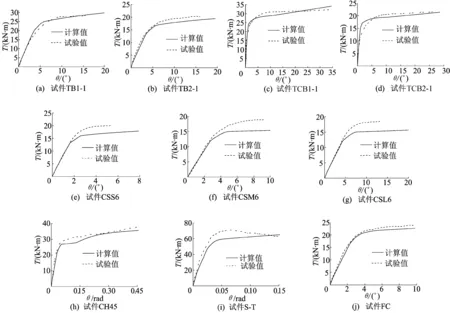
图4 圆、方钢管混凝土试验曲线与计算曲线比较

计算结果表明,计算结果与文献的试验结果吻合较好。在抗扭强度承载力上,有限元计算的抗扭强度与试验测得抗扭强度的比值(Tuc/Tue)的平均值为0.95,均方差为0.01,计算结果总体偏于安全。

本文再将部分椭圆钢管混凝土短柱轴压[1]、偏压[3]的试验曲线与有限元分析曲线进行对比,以进一步验证有限元模型的准确性。椭圆钢管混凝土柱轴压试验曲线[1]与计算曲线比较如图5所示。椭圆钢管混凝土柱偏压试验曲线[3]与计算曲线比较如图6所示。

图5、图6比较结果表明试验曲线和计算曲线基本吻合,本文提出的等效方法适用于椭圆钢管混凝土有限元分析。

图5 椭圆钢管混凝土柱轴压试验曲线与计算曲线比较

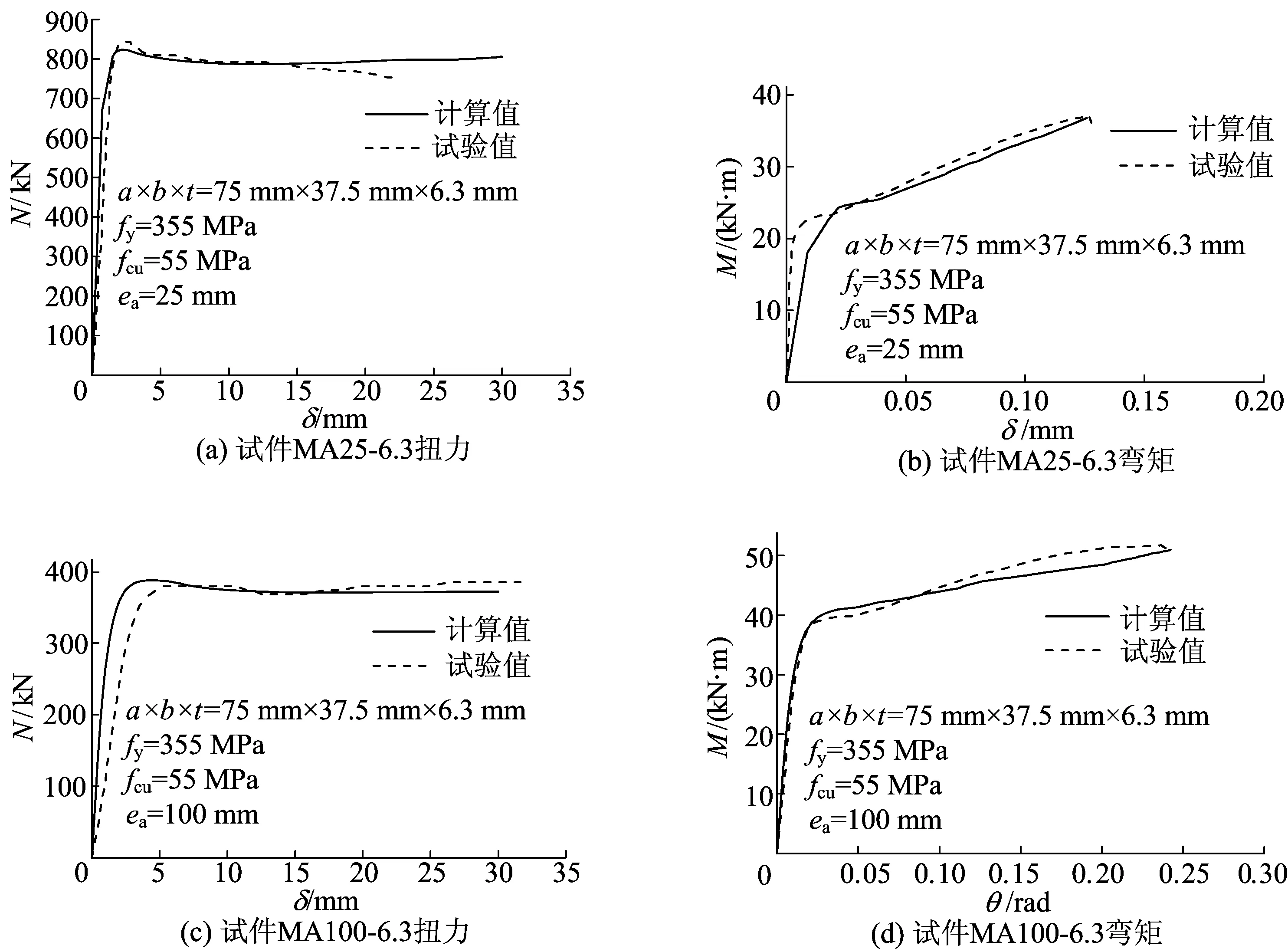
图6 椭圆钢管混凝土柱偏压试验曲线与计算曲线比较

2 参数分析

本文分别研究钢材强度、混凝土强度、径厚比、长短轴比以及截面面积等参数对椭圆钢管混凝土构件抗扭强度承载力的影响。因为椭圆钢管混凝土的扭矩(T)-转角(θ)曲线没有明显的峰值点和下降段,根据大量的曲线分析,发现当构件短轴端部剪应变达到10-1后,构件的扭矩-转角关系曲线已趋于平缓,构件变形增加显著,而扭矩增加很小,所以本文取椭圆钢管混凝土构件短轴端部剪应变为10-1时对应的扭矩为抗扭强度承载力。

为方便研究,引入椭圆钢管混凝土构件的截面含钢率α和套箍系数ξ,其表达式分别为:

α=As/Ac

(4)

(5)

其中,As为椭圆钢管横截面积;Ac为核心混凝土横截面积;fck为混凝土轴心抗压强度标准值。

具体计算参数及分析结果见表2所列,如图7、图8所示。表2中,Tu1为抗扭强度承载力。

表2 有限元计算参数

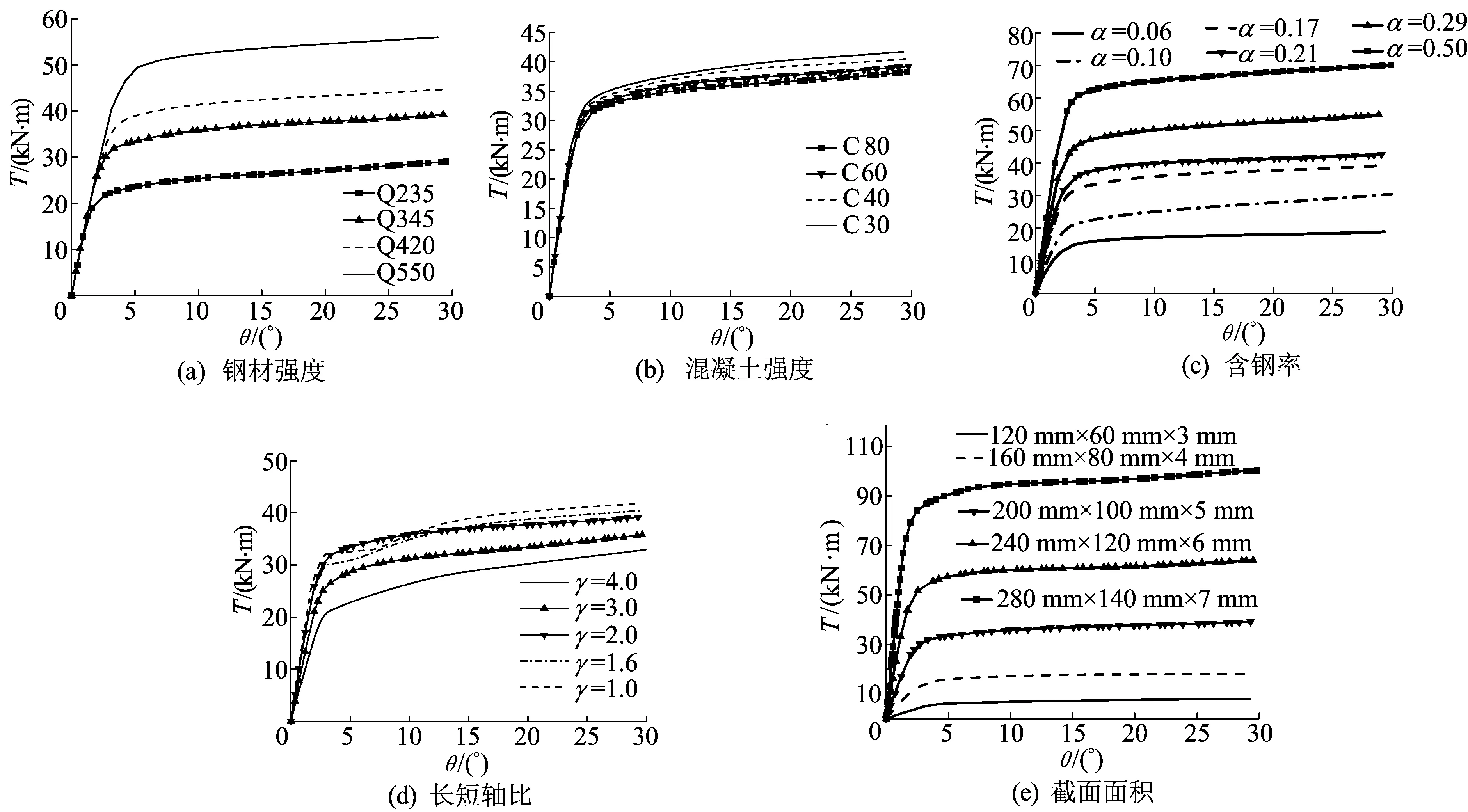
图7 不同参数对扭矩(T)-转角(θ)曲线影响

图8 截面面积比与抗扭强度承载力关系曲线

2.1 钢材强度

由图7a可见,钢材的屈服强度对扭矩-转角曲线的弹性阶段刚度几乎无影响。由表2计算结果表明,与钢材强度Q345相比,钢材强度Q235试件的抗扭强度承载力降低29.4%,钢材强度Q420和Q550试件的抗扭强度承载力分别提高16.0%和45.7%。随着钢材屈服强度的提高,构件的抗扭强度会显著增大。

2.2 混凝土强度

写完给丈夫儿子的遗书，心里有踏实之感。我想，我必须给儿子一些嘱咐，于是拉着儿子的手对他说：“如果飞机掉到海里了，一定要抱住漂浮的东西！”儿子颤抖着的手一直拉着我的手不放……

图7b与表3计算结果表明,混凝土强度C80试件的抗扭强度承载力比混凝土强度C30试件只提高了不到4%。由此可见,混凝土强度对椭圆钢管混凝土的抗扭强度影响很小,但曲线弹性阶段的刚度会随着混凝土强度增大而略有提高。

2.3 含钢率

由图7c可见,T-θ曲线弹性阶段的刚度随截面含钢率增加而有所增大,抗扭强度承载力也会增大,但曲线的形状不会改变。与α=0.17试件相比,α=0.06和α=0.10试件的抗扭强度承载力分别降低了49.5%和27%,α=0.21、α=0.29及α=0.17试件的抗扭强度承载力分别提高了18%、44.2%及98.6%。由此可见,截面含钢率对椭圆钢管混凝土构件的抗扭强度影响较大。

2.4 长短轴比

本文在保证钢材强度、混凝土强度、截面含钢率和截面面积相同的条件下,研究不同长短轴比对椭圆钢管混凝土构件抗扭承载力的影响。长短轴比计算公式为：

γ=a/b

(6)

由图7d和表2可知,在γ≥2时,长短轴比对椭圆钢管混凝土构件的抗扭强度影响很小;γ≤2时,构件抗扭强度随着长短轴比的增加而略微增大,曲线弹性阶段的刚度也随着长短轴比的增大而略有提高。在同等条件下,γ=2的椭圆钢管混凝土构件具有较高的抗扭强度和较好的延性。

2.5 截面面积

为研究椭圆钢管混凝土纯扭构件的尺寸效应,本文在保证钢材强度、混凝土强度、长短轴比和含钢率相同的条件下,给出了不同截面尺寸的椭圆钢管混凝土T-θ关系曲线,如图7e所示。由表2可知,与截面尺寸为200 mm×100 mm×5 mm的试件相比,120 mm×60 mm×3 mm和160 mm×80 mm×4 mm的试件抗扭强度承载力分别降低78.3%和50.1%,240 mm×120 mm×6mm和280 mm×140 mm×7 mm的试件抗扭强度承载力分别提高了67.6%和159.2%。

由图7e和表2可知,截面面积对T-θ关系曲线的形状影响不大,但对构件抗扭强度有较大影响。曲线弹性阶段的刚度和构件抗扭承载力会随着截面面积的增大而显著增大。由图8(图中A0为截面尺寸为120 mm×60 mm×3 mm试件的截面面积,A1为其余4个截面的截面面积)可见,椭圆钢管混凝土构件抗扭强度承载力的增大与截面面积的增加近似成线性关系。

3 受力机理分析

空钢管和椭圆钢管混凝土的钢管在纯扭状态下的典型破坏模态如图9所示。

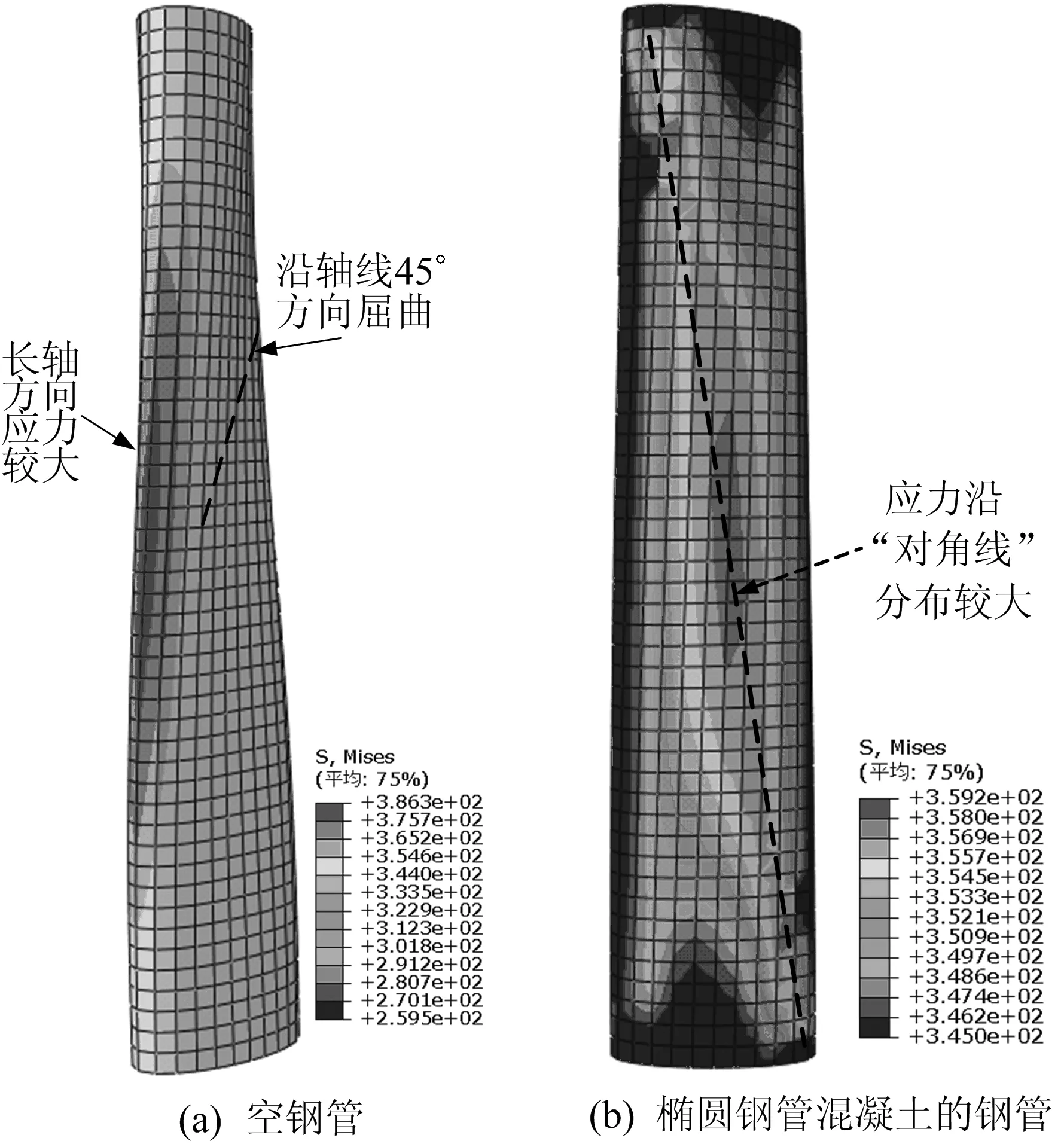
图9 钢管混凝土和空钢管的钢管扭转破坏模态比较

由图9可以看出两者的破坏模态有较大区别,空钢管受扭破坏时长轴方向管壁最先屈服,钢管管壁沿轴线45°方向产生明显屈曲,在椭圆长轴方向应力较大。椭圆钢管混凝土的钢管中应力在短轴方向较大,若把椭圆短轴方向曲率大的面近似看做矩形,则应力沿矩形对角线分布较大,且钢管没有明显屈曲,表现出较好的塑性和稳定性。这说明椭圆钢管内填混凝土能有效地防止钢管内凹屈曲,充分发挥钢材的强度。

3.2 钢管与核心混凝土间的相互作用

椭圆钢管混凝土构件在纯扭作用下,钢管和核心混凝土的相互作用力主要集中在曲率小的地方,在椭圆长轴方向的力要比短轴方向显著。钢管和核心混凝土的相互作用力的大小与椭圆长短轴比γ有关,随着长短轴比γ的减小,钢管对核心混凝土的约束作用逐渐增强,相互作用力的受力面也更加均匀。

3.3 荷载-变形曲线全过程分析

通过大量数值分析,得到了椭圆钢管混凝土构件的T-θ关系曲线,如图10所示,按其受力特点,T-θ曲线大致可以分为3个阶段。

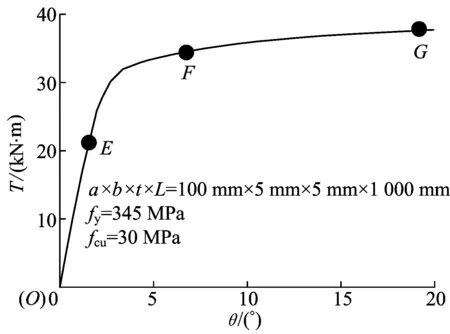
图10 椭圆钢管混凝土柱受扭构件典型T-θ关系曲线

(1) 弹性阶段(OE)。扭矩-转角关系曲线基本呈线性关系,椭圆钢管和核心混凝土只在长轴方向产生相互作用力。E点相当于构件进入弹塑性阶段的起点。

(2) 弹塑性阶段(EF)。进入弹塑性阶段后,钢管开始屈服,核心混凝土在扭矩作用下,裂缝不断开展,钢管和核心混凝土的相互作用力由长轴方向逐渐向全截面扩展。F点相当于构件进入塑性阶段的起点。

(3) 塑性强化段(FG)。钢管全截面屈服,但核心混凝土有效地抑制了椭圆钢管的凹曲,核心混凝土也由于钢管的包裹而不会发生破碎。椭圆钢管混凝土的抗扭强度因而不断增长,表现出较好的塑性性能。

4 抗扭承载力计算公式

根据材料力学理论,椭圆形截面杆的扭转最大切应力发生在椭圆短轴端部,计算公式为:

(7)

其中,Wt=πab2/2。

τscy=X(0.435+0.313α2.33)ξ0.175fesc

(8)

其中,X为长短轴比影响系数;fesc为椭圆钢管混凝土轴压承载力指标。

当γ=1.6时,X=1.5;当γ=2.0时,X=1.7;当γ=3.0时,X=2.1;中间按线性插值法取值。

fesc计算公式[15]为:

fesc=(A+Bξ+Cξ2+Dξ3)fck

(9)

其中,A=1.362 46；B=0.707 95；C=0.062 36；D=-0.007 46。

通过数据拟合得出椭圆钢管混凝土的抗扭强度承载力公式为:

Tu=γtWtτscy

(10)

γt=1.21+0.28ln(ξ/γ)

(11)

(10) 式、 (11) 式适用于Q235～Q550钢材和C30～C80混凝土,α=0.06～0.21,γ=1.6～3.0。

抗扭承载力公式的计算结果与有限元计算结果比较见表3所列。

表3 抗扭承载力计算结果对比

注:Tu1为有限元结果,Tu2为公式计算结果。

计算结果表明,Tuc/Tue的平均值为0.98,均方差为0.004,因此,本文经回归拟合提出的椭圆钢管混凝土抗扭承载力计算公式具有较好的准确性,且计算结果总体偏于安全。

5 结 论

(1) 本文采用椭圆等效截面法[8]和钢管混凝土本构关系模型[9],考虑了钢管与混凝土之间复杂接触问题和边界条件等,建立了椭圆钢管混凝土有限元分析模型。

(2) 影响椭圆钢管混凝土构件抗扭承载力的主要参数有钢材强度、截面含钢率和截面面积。钢材强度越高,截面面积和含钢率越大,抗扭承载力越大。

(3) 纯扭状态下钢管和混凝土的相互作用形式与长短轴比γ有关,随着长短轴比的减小,钢管对核心混凝土的约束作用逐渐增强,相互作用力的受力面也更加均匀。

(4) 椭圆钢管混凝土的T-θ曲线可分为弹性阶段、弹塑性阶段和塑性强化阶段。进入塑性强化阶段以后,扭矩值继续缓慢增长,表现出较好的塑性性能。

(5) 基于钢管混凝土统一理论,提出了椭圆钢管混凝土构件抗扭强度承载力计算公式,并通过有限元计算验证了公式的准确性和可靠性,对此类构件设计具有参考意义。由于目前国内外尚缺乏椭圆钢管混凝土受扭构件的试验数据,后期研究将作进一步的试验验证。

[1] YANG H,LAM D,GARDNER L.Testing and analysis of concrete-filled elliptical hollow sections[J].Engineering Structures,2008,30(12):3771-3781.[2] DAI X H,LAM D,JAMALUDDIN N,et al.Numerical analysis of slender elliptical concrete filled columns under axial compression[J].Thin-Walled Structures,2014,77(4):26-35.[3] SHEEHSAN T,DAI X H,CHAN T M,et al.Structural response of concrete-filled elliptical steel hollow sections under eccentric compression[J].Engineering Structures,2012,45(15):314-323.

[4] 刘习超,查晓雄.椭圆形钢管混凝土构件性能的研究Ⅰ:轴压短柱和长柱[J].建筑钢结构进展,2011,13(1):8-14.

[5] 刘习超,查晓雄.椭圆形钢管混凝土构件性能的研究Ⅱ:纯弯和压弯构件[J].建筑钢结构进展,2011,13(1):15-19.

[6] REN Q X,HAN L H,LAM D,et al.Tests on elliptical concrete filled steel tubular (CFST) beams and columns [J].Journal of Constructional Steel Research,2014,99(8):149-160.

[7] 韩林海.钢管混凝土结构:理论与实践[M].2版.北京:科学出版社,2007:159-170.

[8] ZHAO X L,PACKER J A.Tests and design of concrete-filled elliptical hollow section stub columns[J].Thin-Walled Structures,2009,47(6/7):617-628.

[9] 刘威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学,2005:54-57.

[10] 韩林海,钟善桐.钢管混凝土纯扭转问题研究[J].工业建筑,1995,25(1):7-13.

[11] 徐积善,周竞.钢管混凝土中长柱在压扭复合受力下的试验研究[C]//中国钢协钢-混凝土组合结构协会第三次年会论文集.哈尔滨:中国钢结构协会钢-混凝土组合结构分会,1991:43-50.

[12] BECK J,KIYOMIYA O.Fundemental pure torsional properties of concrete filled circular steel tubes [J].Journal of Materials,Concrete Structures and Pavements,2003,60(739):285-296.

[13] 陈逸玮.钢管混凝土柱形状因素于扭转韧性行为研究[D].台北:中央大学,2003:30-51.

[14] KITADA T,NAKAI H.Experimental study on ultimate strength of concrete-filled square steel short members subjected to compression or torsion [C]//Proceedings of the International Conference on Steel-Concrete Composite Structures.Fukuoka,Japan:International Association for Coorperation and Research of Steel-Concrete Composite Strectures,1991:137-142.

[15] 沈奇罕,王静峰,王伟,等.基于数值分析的椭圆钢管混凝土柱轴压性能及承载力计算[J].建筑钢结构进展,2015,17(6):68-78.

(责任编辑 张淑艳)

Torsional behavior and ultimate torsional strength calculation of ECFST

SONG Shunlong1, WANG Jingfeng2, JIANG Han2, SHEN Qihan2

(1.CCCC Railway Consultants Group Co.， Ltd., Beijing 100097, China; 2.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

To study the torsional behavior and ultimate torsional strength calculation of elliptical concrete-filled steel tube(ECFST) members, the numerical analysis model of the ECFST members subjected to torsional loading was established by ABAQUS software. The parameter analysis of ECFST members under pure torsion was carried out, including steel and concrete strength, steel ratio, sectional area and long-to-short axis ratio. The force mechanism of ECFST members under pure torsion was revealed. A simplified calculating formula of ultimate torsional strength of ECFST members was proposed. The research results indicated that the ultimate torsional strength of ECFST members increased with the increase of steel strength, sectional area and steel ratio. The torsion(T)-angle(θ) curve of ECFST members could be divided into elastic stage, elastic-plastic stage and plastic hardening stage, showing a good plastic property. The calculating formula of ultimate torsional strength can be used in the design of ECFST members.

elliptical concrete-filled steel tube(ECFST) members; finite element; torsional behavior; ultimate torsional strength; force mechanism

2016-05-11；

2017-05-08

国家自然科学基金资助项目 (51478158);教育部新世纪优秀人才支持计划资助项目(NCET-12-0838)

宋顺龙(1976-),男,湖南邵阳人,中交铁道设计研究总院有限公司高级工程师; 王静峰(1976-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师,通讯作者,E-mail:jfwang008@163.com.

10.3969/j.issn.1003-5060.2017.07.018

TU398.9

A

1003-5060(2017)07-0952-08