Crypton算法的不可能差分分析
2017-08-12崔竞一郭建胜刘翼鹏
崔竞一 郭建胜 刘翼鹏
(解放军信息工程大学 郑州 450001)
Crypton算法的不可能差分分析
崔竞一 郭建胜 刘翼鹏
(解放军信息工程大学 郑州 450001)
(xd_cjy@126.com)
Crypton算法是基于Square算法设计的SPN结构类密码算法,由于其具备良好的软硬件性能而引起了广泛的关注.对Crypton分组密码算法在不可能差分分析下的安全性进行了研究.通过分析Crypton算法扩散层的性质,指出了现有7轮Crypton算法不可能差分分析中存在的问题,结合快速排序、分割攻击与早夭技术对7轮Crypton算法的不可能差分分析进行了改进,降低了其数据复杂度与时间复杂度;同时,通过并行使用4条不可能差分区分器,结合密钥扩展算法的性质给出了7轮Crypton算法的多重不可能差分分析结果,恢复了算法的主密钥;最后,在7轮Crypton算法的不可能差分分析的基础上向后拓展1轮,给出了8轮Crypton-256算法的不可能差分分析,恢复了其主密钥,其数据复杂度为2103个选择明文,时间复杂度为2214次8轮Crypton加密,存储复杂度为2154.4B.研究结果表明:结合算法的性质及多种技术给出了Crypton算法目前最优的不可能差分分析结果.
分组密码;密码分析;Crypton;不可能差分分析;早夭技术
AES加密标准面向全球征集了15个候选算法[1],Crypton分组密码算法[2]就是其中之一.Crypton算法是基于Square算法[3]设计的,由于其具有很多优点:使用SPN结构满足加脱密结构相似,具有良好的可证明安全性,同时具有良好的并行能力,能够广泛适用于各类软硬件环境,从而受到广大学者的关注.Crypton算法共有2个版本,通常称作Crypton v0.5[4]与Crypton v1.0[2].设计者对Crypton v0.5的密钥扩展算法与S盒的设计中存在的缺陷进行改进后提出了Crypton v1.0.随着物联网技术与RFID技术的发展,对轻量级密码算法的需求日益增加,Lim等人[5]于2006年参照Crypton算法的设计思路,设计提出了轻量级分组密码算法mCrypton.人们针对Crypton算法与mCrypton算法给出了许多分析结果.1999年Seki等人[6]给出了Crypton算法的不可能差分分析结果;2000年Minier等人[7]给出了Crypton算法的猜测攻击;2001年Cheon等人[8]给出了改进不可能差分分析结果;2003年Kim等人[9]给出了8轮Crypton算法截断差分分析结果;2010年Mala等人[10]利用不可能差分给出了7轮Crypton算法的分析结果;2011年Wei等人[11]给出了Crypton算法的相关密钥不可能差分分析结果;2013年Kang等人[12]给出了Crypton-192256算法与mCrypton-96128算法的碰撞攻击;2014年Song等人[13]给出了全轮Crypton-256算法与mCrypton-128算法的Biclique攻击结果,同时Hao等人[14]给出了mCrypton算法在中间相遇攻击下的安全性研究结果;2015年Shakiba等人[15]进一步完善了全轮Crypton算法的Biclique攻击结果,同时,Shakiba等人[16]与Jeong等人[17]分别对全轮mCrypton算法在Biclique下的安全性进行了讨论;2016年Hao等人[18]给出了10轮Crypton-256算法的中间相遇攻击结果,王高丽等人[19]给出了8轮mCrypton-96算法的中间相遇攻击结果.
不可能差分分析是由Knudsen[20]和Biham等人[21]独立提出的1种单密钥条件下的攻击方法.Knudsen在分析AES候选算法DEAL的安全性时,提出轮函数是双射的Feistel结构存在5轮不可能差分;Biham等人在FSE 1999上介绍了利用中间相遇思想来构造不可能差分的方法.随后,不可能差分成为了研究热门并在许多算法的分析中得到应用.近年来,不可能差分的思想逐渐演化出了多种分析方法,如零相关线性分析[22]、相关密钥不可能差分分析[23].
本文对Crypton算法在不可能差分分析下的安全性进行了研究.结合扩散层性质、早夭技术[24]、分割攻击、快速排序算法[25],改进7轮Crypton算法的不可能差分分析;同时并行利用4个区分器[26],给出7轮Crypton算法的多重不可能差分分析结果;最后,给出首个8轮Crypton-256算法不可能差分分析结果.
1 Crypton算法介绍
1.1 符号说明
xi: 第i轮经过密钥异或σ后的状态;
yi: 第i轮经过非线性变换γ后的状态;
zi:第i轮经过比特置换π后的状态;
wi: 第i轮经过字节移位τ后的状态;
xi,c ol(j):xi状态的第j列;
xi,r ow(j):xi状态的第j行;
ke i: 第i轮加密密钥;
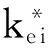
xi[j]: 状态xi的第j个字节;
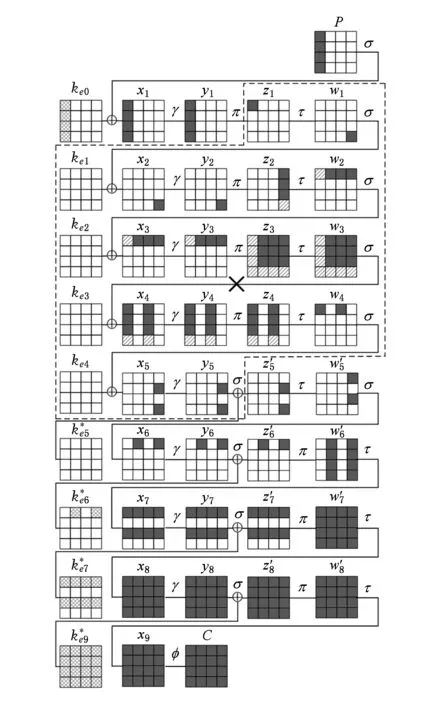
< 1.2 Crypton算法 Crypton v0.5与Crypton v1.0算法仅在S盒与密钥扩展算法处不同,本节以Crypton v1.0为例进行介绍.Crypton算法采用SPN结构,分组规模为128 b,密钥规模为64+32k(0≤k≤6)位,迭代轮数为12轮,本文对算法迭代轮数的标号从1开始记,分别标记为第1轮至第12轮.128 b的分组状态可表示为16 B的形式,如图1所示,其中aij表示第i行第j列的元素. Fig. 1 The state of Crypton图1 Crypton状态表示 Crypton算法的轮函数ρ由非线性变换γ、比特置换π、字节移位τ、密钥异或σ共4个变换组成.下面分别对4个变换进行说明. Fig. 2 The S layers of Crypton图2 Crypton算法的S层 2) 比特置换π.对状态的每1列使用4个字节掩码mi进行置乱,分支数为4,其中m0=0xfc,m1=0xfc,m2=0xcf,m3=0x3f.定义4个列置换πi(0≤i≤3): 算法中包含2个不同的扩散层,奇数轮使用πo,偶数轮使用πe: πo(A)=(π3(A3),π2(A2),π1(A1),π0(A0)); πe(A)=(π1(A3),π0(A2),π3(A1),π2(A0)). 3) 字节移位τ.将位于第i行、第j列的字节移位至第j行、第i列,满足B=τ(A)⟺bij=aji. 4) 密钥异或σ.将密钥字节与状态字节进行异或. 完整的加密流程需要在算法的初始位置异或1个白化密钥,在算法的末尾增加1个出口变换φe=τ∘πe∘τ确保加脱密算法结构相似性,同理可以定义φo=τ∘πo∘τ. Crypton v1.0的密钥扩展算法利用主密钥生成52个32位字节,构成13个圈子密钥.密钥扩展算法分为利用主密钥生成8个扩展密钥和利用扩展密钥生成圈子密钥2个过程. 1) 生成扩展密钥.在主密钥左侧填充0,将规模为64+32k(0≤k≤6)位的主密钥扩充至256 b.令K=k31…k1k0为256 b扩展密钥,将K分为8个32位字节: U[0]=k6k4k2k0,V[0]=k7k5k3k1; U[1]=k14k12k10k8,V[1]=k15k13k11k9; U[2]=k22k20k18k16,V[2]=k23k21k19k17; U[3]=k30k28k26k24,V[3]=k31k29k27k25. 利用U,V按步骤生成扩展密钥Ee: 步骤1.U′=τ∘πo∘γ(U),V′=τ∘πe∘γ(V); 步骤2. fori=0 to 3 生成圈子密钥:利用扩展密钥Ee(k)与13个轮常数Ce[i]、4个掩码常数MCj共同生成13个圈子密钥.其中轮常数Ce[i]与掩码常数MCj的具体形式为 Ce[0]=0xa54ff53a, Ce[i]=Ce[i-1]+0x3c6ef372 mod 232, (i=1,2,…,12); MC0=0xacacacac, (j=1,2,3). 2) 按照2个步骤生成13个圈子密钥. 步骤1. 计算前2轮的圈子密钥Ke[0,1,…,7].对于i=0,1,2,3,计算: Ke[i]=Ee[i]⊕Ce[0]⊕MCi; Ke[i+4]=Ee[i+4]⊕Ce[1]⊕MCi. 步骤2. 计算2~12轮的圈子密钥,对于奇数轮与偶数轮分别使用不同的步骤. 步骤2.1. IFr为偶数*对于偶数轮* {Ee[3],Ee[2],Ee[1],Ee[0]}← Ke[4r+i]←Ee[i]⊕Ce[r]⊕MCi, (i=0,1,2,3); 步骤2.2. IFr为奇数*对于奇数轮* {Ee[7],Ee[6],Ee[5],Ee[4]}← Ke[4r+i]←Ee[4+i]⊕Ce[r]⊕MCi, (i=0,1,2,3). 首先对Crypton算法的差分性质进行研究,其次构造Crypton算法的2类4轮不可能差分区分器. 2.1 相关性质 性质1. 在Crypton算法中,所有奇数轮(偶数轮)圈子密钥的对应字节之间存在一一映射关系,已知奇数轮(偶数轮)圈子密钥的1 B,可以求出其他奇数轮(偶数轮)圈子密钥的对应字节. 证明. 在奇数轮(偶数轮)圈子密钥的生成算法中,独立使用4个扩展密钥生成圈子密钥,且在生成圈子密钥时,32 b块的循环移位是以8 b16 b24 b进行的,1个输出字节仅与对应的1个输入字节有关.因此,各奇数轮(偶数轮)圈子密钥字节与字节之间存在一一映射关系. 证毕. 性质2. 在Crypton算法中,当已知任意1个奇数轮圈子密钥与任意1个偶数轮圈子密钥时,可以恢复主密钥. 证毕. 类比文献[10]中的结论,可以给出Crypton算法最后1轮复合输出变换的差分特性. 性质3. 当仅考虑截断差分传递规律时,Crypton算法的最后1轮的τ∘π变换与输出变换φ=τ∘π∘τ可合并为1个字节移位变换,同时满足πe∘πo=πo∘πe. 证明. 仅考虑差分传递时,当减轮Crypton算法为奇数轮时,最后1轮τ∘πo与输出变换φe=τ∘πe∘τ可以合并为1个字节移位变换;当减轮Crypton算法为偶数轮时,最后1轮τ∘πe与输出变换φo=τ∘πo∘τ也可以合并为1个字节移位变换.下面以奇数轮的Crypton算法为例进行证明,偶数轮的Crypton算法可以同理证明得到. 由于密钥模加变换相对于异或操作是线性的,因此在考虑字节的异或差分传递时可以忽略密钥模加操作,则最后1轮与输出变换复合后得τ∘πe∘πo.令a为非线性变换层的输出且满足τ∘πe∘πo(a)=c,若c′=τ(c),b=πo(a)则有πe∘πo(a)=c′. b3=m3a3⊕m0a7⊕m1a11⊕m2a15; b7=m0a3⊕m1a7⊕m2a11⊕m3a15; b11=m1a3⊕m2a7⊕m3a11⊕m0a15; b15=m2a3⊕m3a7⊕m0a11⊕m1a15. 证毕. 性质4. 当Crypton算法的π变换满足输入2 B差分活动,输出2 B差分活动时,必满足输入2 B的差分值与输出2 B的差分值相同且取特定差分值,共有4组差分对应: 1) 第1组.其中x=0x1,0x2,0x3, (x,x,0,0)→(x,0,0,x), (0,x,x,0)→(0,0,x,x), (x,0,x,0)→(x,0,x,0), (0,x,0,x)→(0,x,0,x), (x,0,0,x)→(x,x,0,0), (0,0,x,x)→(0,x,x,0). 2) 第2组.其中x=0x4,0x8,0xc, (x,x,0,0)→(x,x,0,0), (0,x,x,0)→(x,0,0,x), (x,0,x,0)→(0,x,0,x), (0,x,0,x)→(x,0,x,0), (x,0,0,x)→(0,x,x,0), (0,0,x,x)→(0,0,x,x). 3) 第3组.其中x1=0x10,0x20,0x30, x2=0x10,0x11,0x12,0x13,0x20,0x21,0x22,0x23,0x30,0x31,0x32,0x33, (x1,x1,0,0)→(0,x1,x1,0), (0,x1,x1,0)→(x1,x1,0,0), (0,0,x1,x1)→(x1,0,0,x1), (0,x2,0,x2)→(0,x2,0,x2), (x1,0,0,x1)→(0,0,x1,x1), (x2,0,x2,0)→(x2,0,x2,0). 4) 第4组.其中x1=0x40,0x80,0xc0, x2=0x40,0x44,0x48,0x4c,0x80,0x84,0x88,0x8c,0xc0,0xc4,0xc8,0xcc, (x1,x1,0,0)→(0,0,x1,x1), (0,x1,x1,0)→(0,x1,x1,0), (0,0,x1,x1)→(x1,x1,0,0), (0,x2,0,x2)→(x2,0,x2,0), (x1,0,0,x1)→(x1,0,0,x1), (x2,0,x2,0)→(0,x2,0,x2). 其中,x代表非0差分字节,0代表字节差分为0. 性质5[14]. 随机给定Crypton算法S盒的1对输入差分与输出差分对应,平均可以确定1对S盒的输入与输出. 2.2 2类4轮不可能差分区分器 定理1. 区分器I.当τ变换输入状态中仅有1 B为差分活动字节时,经过4轮Crypton算法加密后,γ变换输出状态仅在1列中有2个差分活动字节是不可能的. 证明. 当输入状态中仅有1 B为差分活动时,经过1轮Crypton算法加密后,π变换的输出至少有3个差分活动字节.经过1.5轮Crypton算法加密后,输出一定至少存在9个差分活动字节,至多有1列不含差分活动字节. 当输出状态中仅有1列中含有2个差分活动字节时,经过1.5轮Crypton算法解密后,必存在2列不含有差分活动字节,因此产生矛盾. 证毕. 当取输入状态中第3个字节为差分活动时,经过4轮Crypton算法加密后,输入状态中不可能仅在第8个字节与第12个字节处为差分活动.具体形式图3所示,灰色表示差分活动字节,斜线表示该字节可能存在差分,白色表示该字节非差分活动. Fig. 3 4-round impossible differential distinguisher图3 4轮不可能差分区分器 定理2. 区分器I的对偶形式.当τ变换输入状态同一列任意2 B为差分活动字节时,经过4轮Crypton算法加密后,γ变换的输出状态不可能仅有1个差分活动字节. 证明. 当τ变换输入状态同一列中存在2个差分活动字节,则经过γ∘τ变换后,下一轮π变换的输入必有1行中含有2个差分活动字节,经过π变换后必有2列为非差分活动的. 若最后1轮γ变换后的输出状态中仅有1个差分活动字节,则向上推导可知在π-1变换的输入中仅有1个差分活动字节,经过π-1变换后该行必至少存在3个差分活动字节.经过τ-1变换与π-1变换后,必存在3列有差分活动字节,从而产生矛盾,形成了1个不可能差分对应. 证毕. 利用定理1中构造的区分器I,改进7轮Crypton算法的不可能差分分析,恢复最后1轮圈子密钥;同时通过并行利用4条定理2给出的不可能差分区分器,恢复7轮Crypton算法的主密钥. 3.1 改进的7轮Crypton算法不可能差分分析 文献[10]使用定理1中所给出的区分器,对7轮Crypton算法进行了攻击,恢复了第7轮的圈子密钥.通过进一步研究发现,上述攻击存在2个问题: 1) 根据性质4,当输出差分模式满足(0,0,1,1)时,输入差分模式不存在(0,0,1,1)的形式; 2) 根据性质4,当输出差分第11,15 B差分活动,而输入差分为任意2 B差分活动时,仅存在15个可能的差分对应,因此其概率应为2-12.4而非2-11.8. 基于定理1中的4轮不可能差分区分器,结合扩散层性质、快速排序算法、分割攻击与早夭技术[27]改进7轮Crypton算法的不可能差分分析.攻击过程分为预计算与在线攻击2个阶段. 1) 在预计算阶段需要预计算并存储3个表 ① 表T1.满足第3列中仅有1 B差分活动,其余字节为非差分活动的差分状态Δz1,c ol(3)共有210种取值.因此,S盒输出差分Δy1,c ol(3)共有210种取值,根据性质5,给定S盒输入差分Δx1,col(3),平均能够确定出210个y1,c ol(3).同时,由于Δx1,col(3)=ΔPc ol(3),表T1以232个明文差分ΔPc ol(3)为索引,存储对应的210个x1,col(3). ② 表T2.对于仅在第0个字节处差分活动的状态对Δz6,c ol(0)′,共有28种可能取值.根据性质5,表T2以232个密文差分ΔCc ol(2)为索引,存储28个(z6′[0],z6″[0])和对应的y7,row(0). ③ 表T3.类似表T2,对于仅在第2个字节处为差分活动的状态对Δz6,col(2)′,共有28种可能取值.因此以232个ΔCc ol(0)为索引,存储28个(z6′[2],z6″[2])和y7,row(2). 2) 在线攻击阶段包含6个步骤: 步骤1. 选择2n1个明文结构,其中明文满足在第3,7,11,15字节上取所有的值,在其余字节上取固定值,1个明文结构包含232个明文,可以构造263个明文对.因此攻击的选择明文量为2n1+32,其中包含2n1+63个明文对. 步骤2. 运用快速排序算法筛选明文对.根据性质3,筛选出密文在第0,2,4,6,8,10,12,14字节差分活动,其余字节差分不活动的明文对,剩余2n1-1个明文对.以明文对序号作索引,将筛选得到的明文对存储在表Ω中,存储明文的第3,7,11,15字节与密文的第0,2,4,6,8,10,12,14字节. 具体的攻击路径如图4所示,其中黑色表示差分活动字节,白色表示差分为0的字节,斜线表示可能存在差分的字节,网状表示猜测的密钥字节.定理3给出上述7轮Crypton算法不可能差分分析的复杂度分析结果. Fig. 4 Impossible differential attack on 7-round Crypton图4 7轮Crypton算法不可能差分分析 定理3. 利用4轮不可能差分区分器能够对7轮Crypton算法进行不可能差分分析,恢复第7轮的圈子密钥,其时间复杂度为2112.6,数据复杂度为2120.4,存储复杂度为299.1. 证明. 预计算阶段与在线攻击阶段的复杂度相差较大,在线攻击阶段的复杂度占主要部分,可以忽略预计算阶段的复杂度. 在线攻击阶段各步骤的复杂度如下: 步骤2快速排序筛选明文对的时间复杂度为2n1×232lb 232=2n1+37次比较,表Ω顺序存储2n1-1个明密文对,其中包含明文4B,密文8B,存储复杂度为2n1-1×2×(4+8)=2n1+2×3B. 步骤3对2n1-1个明文对查找表T2并存储的时间复杂度为2n1-1×28=2n1+7次查表,表Ω1需要存储2B与明文对序号,其存储复杂度为2n1-25×232×(2+(n1-1)8)B. 证毕. 上述7轮不可能差分分析没有利用密钥扩展算法的信息泄漏规律,而且复杂度较低,因此适用于128 b192 b256 b共3种密钥规模的算法. 3.2 7轮Crypton算法多重不可能差分分析 使用定理2中的区分器,仅改变区分器输出的差分活动字节分别为第0,1,2,3 字节,则4条区分器具有相同输入,通过选取相同的明文结构,并行利用4条不可能差分路径,结合密钥扩展算法性质可以给出7轮Crypton算法多重不可能差分分析,恢复算法主密钥.攻击过程分为预计算阶段与在线攻击阶段. 在预计算阶段,需要预计算并存储6个表. 表T4:仅在第15 B差分非0的差分Δz1,c ol(3)共有28种可能取值,可以得到S盒的输出差分Δy1,c ol(3).由明文对可以得到S盒的输入差分Δx1,col(3),根据性质5可以求出28个x1,col(3),将x1,col(3)和(z1[15], 在线攻击阶段共包含8个步骤: 步骤1. 选择2n2个明文结构,其中的明文满足在第1,3,5,7,9,11,13,15字节取所有值,在其余字节上固定.1个明文结构包含264个明文,可构造2127个明文对,因此选择明文量为2n2+64,明文对2n2+127个. 步骤2. 对i=0,1,2,3,分别运用快速排序算法筛选明文对.若i=3,保留密文在第1,5,9,13字节的差分活动,其余字节差分为0的明文对,筛选后剩余2n2+31个明文对.以明文对序号为索引,将剩余明文对存储在表Γi中,存储明文的第1,3,5,7,9,11,13,15字节与密文的第1,5,9,13字节. 步骤5. 由密钥ke 0,c ol(1,3)的当前值求解ke 1[7,15].由表Ω2中2n2-17个明文对,可以得到S盒的输入差分Δx2[7,15].根据性质4,S盒的输出差分满足Δy2[7]=Δy2[15].对Δy2[7]的取值进行穷举,由性质5可以求出(x2[7,15],y2[7,15]),从而可以确定密钥ke 1[7,15].以密钥ke 1[7,15]的216个可能的取值为索引,将满足区分器的明文序号存储在表Ω3中.1个ke 1[7,15]平均剩余明文对个数2n2-17×30216=2n2-28.1. 步骤7. 对密钥(ke 0,c ol(1,3),ke 1[7,15]),在i=0,1,2时,分别进行下面2步检测: 步骤7.1. 对Γi中的明文对,加密1轮后,若输出在第1行与第3行中差分活动字节多于1个或者2个差分活动字节不在同一列,则丢弃该明文对;否则加密至第2轮π变换后,若仅有1列包含2个差分活动字节,其余字节均非差分活动,则保留该明文对.平均剩余明文对个数为2n2+31×2-48×3065 025=2n2-28.1. 攻击路径如图5所示,定理4给出7轮Crypton算法多重不可能差分分析的复杂度分析结果. Fig. 5 Multiple impossible differential attack on 7-round Crypton图5 7轮Crypton算法多重不可能差分分析 定理4. 并行利用4条不可能差分区分器可以恢复7轮Crypton算法的主密钥,其时间复杂度为2115.2,数据复杂度为2120.9,存储复杂度为2101.8. 证明. 步骤2分别对4组2n2+64个明文进行快速排序筛选的时间复杂度为4×2n2×264lb 264=2n2+72次比较,对4组2n2+31个明密文进行存储,存储复杂度为4×2n2+31×2×(4+8)=2n2+36×3 B. 步骤3对2n2+31个明文对查表T5并存储的时间复杂度为2n2+31×28=2n2+39次查表,表Ω1的存储复杂度为232×2n2+7×(2+(n2+31)8)B. 步骤4在ke 0,c ol(1)下,对2n2+7个明文对查表T4的时间复杂度为2n2+7×232×28=2n2+47次查表,表Ω2的存储复杂度为232×2n2-17×(4+(n2+31)8)B. 步骤5的时间复杂度为264×2n2-17×28=2n2+55次查表,存储复杂度为216×2n2-28.1×(n2+31)8B. 步骤6利用类似3.1节中的早夭技术,时间复杂度为280×225.6×210=2115.6次查表. 错误密钥(ke 0,c ol(1,3),ke 1[7,15])通过步骤6检测概率为q=1-[1-(1-2-22)2n2-28.1]232≈1-[1-e-222×2n2-28.1]232≈1-e-232×e-222×2n2-28.1≈1-e-232-1.4425×2n2-50.1,因此能够通过步骤6检测的密钥个数为280×q≈280(1-e-232-1.4425×2n2-50.1). 步骤7分2个子步骤,对于i=0,1,2,步骤7.1的时间复杂度可以忽略不计,通过步骤7.2中检测的概率为q′=1-e-232-1.4425×2n2-50.1,则步骤7.2的时间复杂度为280×225.6×210×q×(q′)i次查表.步骤6与步骤7的时间复杂度之和不超过2115.6×4次查表. 步骤8的候选密钥量为280+4×32×[(1-2-22)2n2-28.1]4≈2208-1.4425×2n2-50.1,对剩余的候选密钥依次穷举8 B,总的计算复杂度为2208-1.442 5×2n2-50.1×264次加密.取n2=56.9时,时间复杂度主要由步骤2所决定2115.2,数据复杂度为2120.9,存储复杂度为2101.8. 证毕. 7轮Crypton算法多重不可能差分分析没有利用密钥扩展算法的信息泄漏规律,而且复杂度较低,因此适用于128 b192 b256 b共3种密钥规模的算法. 本节在3.1节中7轮Crypton算法不可能差分分析的基础上向后拓展1轮,结合密钥扩展算法与扩散层的性质,利用分割攻击思想给出8轮Crypton-256算法的不可能差分分析过程及复杂度分析结果.攻击分为预计算阶段与在线攻击阶段. 预计算阶段需要预计算并存储5个表. 表T5:穷举210个差分Δz1,c ol(3),以232个明文差分ΔPc ol(3)为索引,存储对应的210个x1,col(3). 在线攻击阶段包含8个步骤: 步骤1. 选择2n个明文结构,其中的明文满足在第3,7,11,15 B上取所有的值,在其余字节上取固定值,1个明文结构包含232个明文,可以构造263个明文对.因此攻击的选择明文量为2n+32,将2n+63个明文对以明文序号为索引存储在表Ω1中. Fig. 6 Impossible differential attack on 8-round Crypton-256图6 8轮Crypton-256算法不可能差分分析 图6给出了8轮Crypton算法的不可能差分分析的具体路径,定理5给出其复杂度分析结果. 定理5. 8轮Crypton-256算法的不可能差分分析能够恢复最后1轮圈子密钥,其时间复杂度为2213,数据复杂度为2103,存储复杂度为2154.4. 证明. 以表1的形式给出8轮Crypton-256算法不可能差分分析中各步的时间复杂度与存储复杂度. Table 1 Complexity of Impossible Differential Attack on 8-round Crypton-256表1 8轮Crypton-256算法不可能差分分析复杂度 E: One round encryption. 控制经过步骤8后剩余的候选密钥量2192×(1-2-14.9)2n-49=1时,得到n=71.时间复杂度为2213次8轮Crypton-256算法加密,存储复杂度为2154.4B,数据复杂度为2103个选择明文. 证毕. 定理6. 8轮Crypton-256算法的不可能差分分析能够恢复256 b主密钥,其时间复杂度为2214,数据复杂度为2103,存储复杂度为2154.4. 本文对Crypton算法在不可能差分分析下的安全性进行了研究.指出了文献[10]中对Crypton算法不可能差分分析中差分传递概率估计与攻击路径表示中的错误,并运用π变换性质、分割攻击、早夭技术、快速排序算法改进了7轮Crypton算法不可能差分分析结果;同时并行使用4条不可能差分区分器,结合密钥扩展算法的性质恢复了7轮Crypton算法的主密钥;向后拓展1轮后给出了8轮Crypton算法的不可能差分分析并对其复杂度进行了分析.本文结果与现有Crypton算法的不可能差分分析结果对比如表2所示: Table 2 Comparison of Impossible Differential Attacks on Crypton表2 Crypton算法不可能差分分析结果对比 目前,针对Crypton算法的研究多集中于中间相遇攻击、不可能差分分析和Biclique攻击等单密钥情况下的分析,而Crypton算法的密钥扩展算法较弱,能否进一步结合密钥扩展算法中的弱点,给出更高轮数的攻击或者复杂度更低的相关密钥条件下的攻击结果是下一步研究的重点. [1]Biham E. A note on comparing the AES candidates[EBOL]. 1998 [2016-06-02]. http:csrc.nist.govarchiveaesround1conf2papersbiham2.pdf [2]Lim C. A revised version of Crypton-Crypton V1.0[G]LNCS 1636: Proc of Fast Software Encrypton. Berlin: Springer, 1999: 31-45 [3]Daemen J, Knudsen L, Rijmen V. The block cipher Square[G]LNCS 1267: Proc of Fast Software Encryption. Berlin: Springer, 1997: 149-165 [4]Lim C. Crypton: A new 128-bit block cipher[EBOL]. 1998 [2016-06-01]. http:citeseerx.ist.psu.eduviewdocdownload?doi=10.1.1.52.5771&rep=rep1&type=pdf [5]Lim C, Korkishko T. mCrypton—A lightweight block cipher for security of low-cost RFID tags and sensors[G]LNCS 3786: Proc of Information Security Applications. Berlin: Springer, 2006: 243-258 [6]Seki H, Kaneko T. Cryptanalysis of five rounds of Crypton using impossible differentials[G]LNCS 1716: Proc of ASIACRYPT. Berlin: Springer, 1999: 43-51 [7]Minier M, Gilbert H. Stochastic cryptanalysis of Crypton[G]LNCS 1978: Proc of Fast Software Encryption. Berlin: Springer, 2000: 121-133 [8]Cheon J H, Kim M J, Kim K, et al. Improved impossible differential cryptanalysis of Rijndael and Crypton[G]LNCS 2288: Proc of Information Security and Cryptology. Berlin: Springer, 2001: 39-49 [9]Kim J, Hong S, Lee S, et al. Truncated differential attacks on 8-round Crypton[G]LNCS 2971: Proc of Information Security and Cryptology. Berlin: Springer, 2003: 446-456 [10]Mala H, Shakiba M, Dakhilalian M. New impossible differential attacks on reduced-round Crypton[J]. Computer Standards & Interfaces, 2010, 32(4): 222-227 [11]Wei Yuechuan, Li Chao, Sun Bing. Related-key impossible differential cryptanalysis on Crypton and Crypton v1.0[G]Proc of World Congress on Internet Security. Piscataway, NJ: IEEE, 2011: 227-232 [12]Kang J, Jeong K, Sung J, et al. Collision attacks on AES-192256, Crypton-192256, mCrypton-96128, and Anubis[JOL]. Journal of Applied Mathematics, 2013: Article ID 713673 [2016-08-22]. http:www.hindawi.comjournalsjam2013713673 [13]Song J, Lee K, Lee H. Biclique cryptanalysis on the full Crypton-256 and mCrypton-128[JOL]. Journal of Applied Mathematics, 2014: Article ID 529736 [2016-08-22]. http:www.hindawi.comjournalsjam2014529736citations [14]Hao Yonglin, Bai Dongxia, Li Leibo. A meet-in-the-middle attack on round-reduced mCrypton using the differential enumeration techniques[G]LNCS 8792: Proc of Network and System Security. Berlin: Springer, 2014: 166-183 [15]Shakiba M, Dakhilalian M, Mala H. Cryptanalysis of mCrypton-64[J]. International Journal of Communication Systems, 2015, 28(8): 1401-1418 [16]Shakiba M, Dakhilalian M, Mala H. Non-isomorphic biclique cryptanalysis of full-round Crypton[J]. Computer Standards & Interfaces, 2015, 41: 72-78 [17]Jeong K, Kang H, Lee C, et al. Weakness of lightweight block ciphers mCrypton and LED against biclique cryptanalysis[J]. Peer-to-Peer Networking and Applications, 2015, 8(4): 716-732 [18]Hao Yonglin. Improved meet-in-the-middle on round-reduced Crypton-256[EBOL]. [2016-05-21]. https:eprint.iacr.org2016267.pdf [19]Wang Gaoli, Gan Nan. A meet-in-the-middle attack on 8-round mCrypton-96[J]. Journal of Computer Research and Development, 2016, 53(3): 666-673 (in Chinese)(王高丽, 甘楠. mCrypton-96算法的改进中间相遇攻击[J]. 计算机研究与发展, 2016, 53(3): 666-673) [20]Knudsen L R. DEAL-A 128-bit block cipher[EBOL]. 1998 [2016-06-02]. http:repo.hackerzvoice.netdepot_madchatcryptohash-lib-algodealdeal.pdf [21]Biham E, Bivyukov A, Shamir A. Miss in the middle on IDEA and Khufu[G]LNCS 1636: Proc of Fast Software Encryption. Berlin: Springer, 1999: 124-138 [22]Sun Bing, Liu Zhiqiang, Rijmen V, et al. Links among impossible differential, integral and zero correlation linear cryptanalysis[G]LNCS 9215: Proc of CRYPTO. Berlin: Springer, 2005: 95-115 [23]Wei Hongru, Yin Guangli. Related-key impossible differential cryptanalysis on LBlock[J]. Journal of Computer Research and Development, 2014, 51 (7): 1520-1526 (in Chinese)(卫宏儒, 殷广丽. LBlock算法的相关密钥不可能差分分析[J]. 计算机研究与发展, 2014, 51(7): 1520-1526) [24]Lu Jiqiang, Kim J, Keller N, et al. Improving the efficiency of impossible differential cryptanalysis of reduced Camellia and MISTY1[G]LNCS 4964: Proc of Topics in Cryptology. Berlin: Springer, 2008: 370-386 [25]Zhang Qinggui. Plaintext pair sieve methods in impossible differential attack[J]. Computer Engineering, 2010, 36(2): 127-129 (in Chinese)(张庆贵. 不可能差分攻击中的明文对筛选方法[J]. 计算机工程, 2010, 36(2): 127-129) [26]Li Rongjia, Jin Chenhui. Meet-in-the-middle attacks on 10-round AES[J]. Designs, Codes and Cryptography, 2016, 80(3): 459-471 [27]Hu Hongjian, Jin Chenhui, Li Xinran. Improved impossible differential attack on 7-round AES -128[J]. Journal of Cryptologic Research, 2015, 2(1): 92-100 (in Chinese)(胡弘坚, 金晨辉, 李信然. 改进的7轮AES -128的不可能差分攻击[J]. 密码学报, 2015, 2(1): 92-100) Cui Jingyi, born in 1992. Master candidate. His main research interests include design and cryptanalysis of symmetric cipher. Guo Jiansheng, born in 1972. Professor and PhD supervisor. His main research interests include information security and cryptology theory. Liu Yipeng, born in 1992. Master candidate. His main research interests include information security and quantum cryptology (lyp_31@126.com). Impossible Differential Attack on Crypton Cui Jingyi, Guo Jiansheng, and Liu Yipeng (ThePLAInformationEngineeringUniversity,Zhengzhou450001) Crypton is one of the candidates of AES that designed based on Square which is a SP-network block cipher. Crypton attracts much attention of the world because of its excellent performance on hardware. The security of Crypton block cipher under impossible differential attack was studied in this paper. The properties of the diffusion layer and nonlinear layer of Crypton are analyzed and combined with the quick sort technique, the divide-and-conquer strategy, the early abort technique, the impossible differential attack on 7-round Crypton is improved with a lower data complexity and time complexity. By using 4 impossible differential distinguishers in parallel, combined with the property of key schedule, the master key of 7-round Crypton is recovered. Based on the impossible differential attack on 7-round Crypton, one more round is extended to maintain the attack on 8-round Crypton-256 to recover the 256-bit key with a data complexity of 2103chosen plaintexts, a time complexity of 22148-round encryptions, a memory complexity of 2154.4B. The results show that with the usage of several techniques and the properties of Crypton, the best impossible differential attacks on Crypton are proposed in this paper known before. These techniques can also be used to analyze the other SP-network block ciphers. block cipher; cryptanalysis; Crypton; impossible differential attack; early abort technique 2016-06-12; 2016-08-31 中国博士后科学基金项目(2014M562582) This work was supported by the China Postdoctoral Science Foundation (2014M562582). 郭建胜(tsg_31@126.com) TP309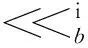






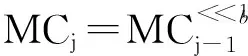
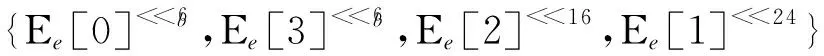

2 Crypton算法的不可能差分性质
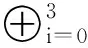




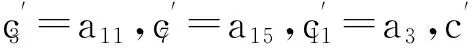
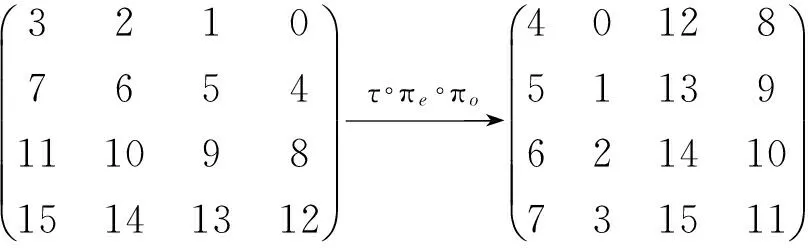

3 7轮Crypton算法不可能差分分析


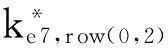



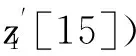
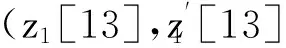
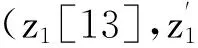



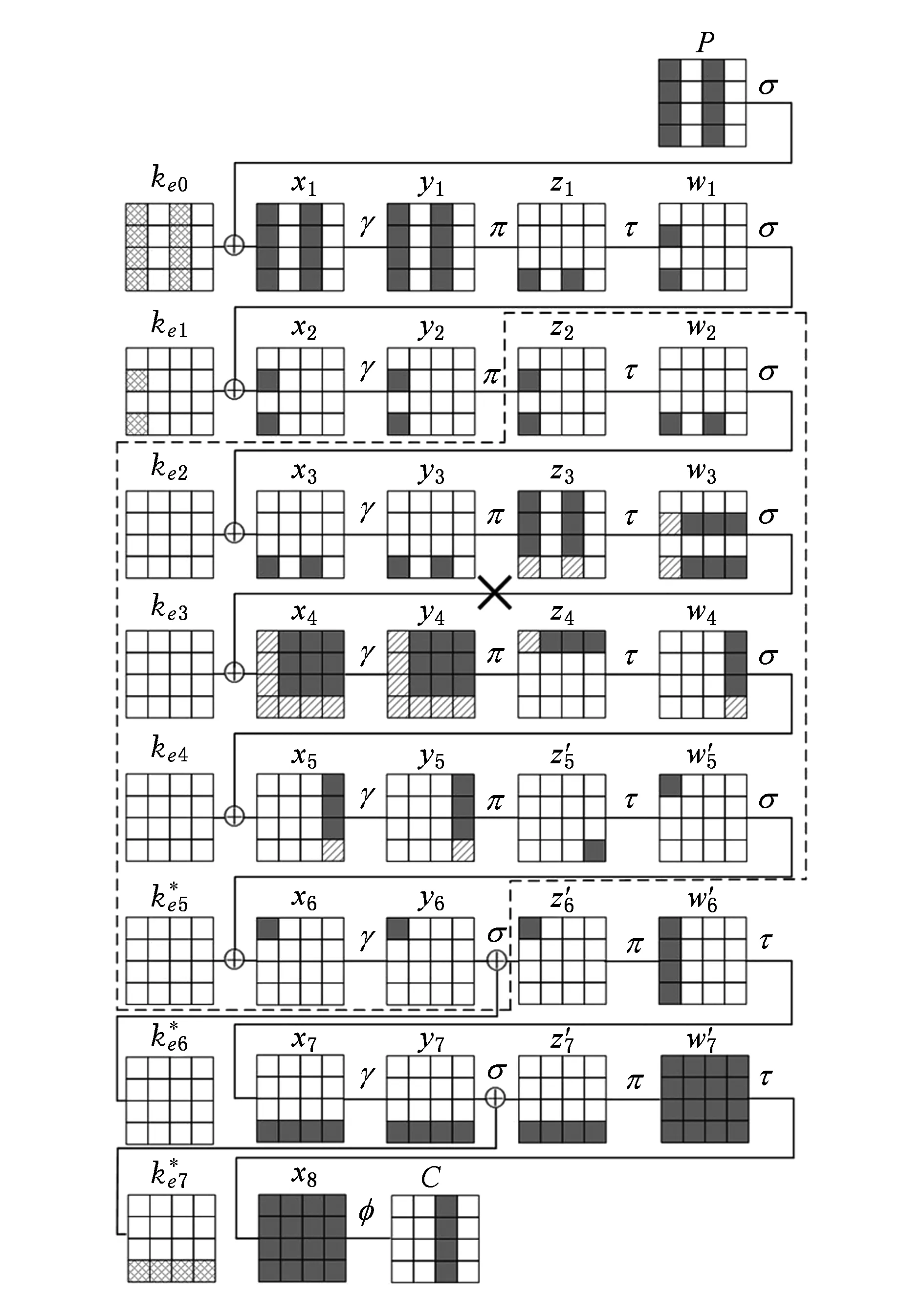
4 8轮Crypton-256算法不可能差分分析




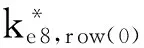


5 结束语




