基于图和改进K近邻模型的高效协同过滤推荐算法

孟桓羽 刘 真 王 芳 徐家栋 张国强

1(北京交通大学计算机与信息技术学院 北京 100044)2(北京交通大学信息中心 北京 100044)3 (南京师范大学计算机科学与技术学院 南京 210023)



基于图和改进K近邻模型的高效协同过滤推荐算法

孟桓羽1刘 真1王 芳2徐家栋1张国强3

1(北京交通大学计算机与信息技术学院 北京 100044)2(北京交通大学信息中心 北京 100044)3(南京师范大学计算机科学与技术学院 南京 210023)

(huanyum@bjtu.edu.cn)

在互联网高速发展的今天，推荐系统已成为解决信息过载的有效手段，能够缓解用户在筛选感兴趣信息时的困扰，帮助用户发现有价值的信息.推荐系统中的协同过滤推荐算法，因其领域无关性及支持用户发现潜在兴趣的优点被广泛应用.由于数据的规模过大且稀疏的特点，当前协同过滤在算法实时性、推荐精确度等方面仍有较大提升空间.提出了GK-CF方法，通过建立基于图的评分数据模型，将传统的协同过滤算法与图计算及改进的KNN算法结合.通过图的消息传播及改进的相似度计算模型对用户先进行筛选再做相似度计算；以用户-项目二部图的节点结构为基础，通过图的最短路径算法进行待评分项目的快速定位.在此基础上，进一步通过并行图框架对算法进行了并行化实现及优化.在物理集群环境下进行了实验，结果表明，与已有的协同过滤算法相比，提出的GK-CF算法能够很好地提高推荐的准确度和评分预测的准确性，并具有较好的算法可扩展性和实时性能.

协同过滤；社会网络；图模型；K近邻；最短路径

随着信息技术和互联网的快速发展，大众对社会化网络的参与和关注程度也越来越高，全球最大的社交网站Facebook的日用户数量在2015年第4季度已经突破10亿，国内的社交网站新浪微博日活跃用户数也达到1亿.据中国电子商务研究中心监测数据显示，截止2015年12月，国内著名电商网站年度活跃用户数增长至1.536亿，同比增长70%.人们逐渐从信息匮乏的时代走入了信息过载的时代，用户在海量信息中选择自己可能感兴趣的信息的难度也逐日增加.为了缓解用户在筛选信息时的困扰，社会网络推荐系统应运而生.据世界最大电商亚马逊的统计，推荐系统对亚马逊销售额贡献率在20%～30%.社交网络推荐主要是指通过挖掘分析用户在社交网络中的社会关系或历史兴趣，结合推荐系统算法，对用户进行各种推荐.比如，通过挖掘用户在社交网络中的好友关系从而为用户推荐新的可能感兴趣的用户或者项目.

随着20世纪90年代协同过滤算法的提出，推荐系统已经成为用户用来对过量互联网信息过滤的一种重要手段[1].作为推荐系统最重要且应用最广泛的一种推荐算法，协同过滤算法的基本思想是根据用户对项目或信息的偏好，发现项目或内容本身的相关性或者是发现用户的相关性.例如，用户甲和用户乙对某类项目恰巧有相同的偏好，那么，协同过滤在对用户甲进行推荐的时候，就会更看重那些曾经被用户乙选择过而用户甲还没有注意到的那些项目.由于协同过滤算法主要利用用户项目评分矩阵来计算项目或者用户之间的相似度，并不要求用机器可以理解的语言来对项目进行详细的描述，属于领域无关的，所以，学术界和工业界经常将协同过滤算法应用到社会网络推荐中.

但是，当前的社会网络用户-项目二部图中，用户基数大但活跃度有限，因此，用户项目评分数据集的密度很小，即稀疏度高.采用降维的矩阵分解算法，算法的计算复杂度过高，计算效率低.在采用奇异值分解(singular value decomposition, SVD)等矩阵分解的方法时，也容易导致过度拟合[2].此外，大多数社会网络推荐算法假设推荐的项目之间是相互独立的，仅着眼于用户，使得推荐的精确度不高.

近年来，随着分布式并行图框架的出现，学术界和工业界将图模型应用于社会网络数据关系建模，并在利用高效的分布式并行图框架的基础上运用图算法来支持机器学习和数据挖掘.针对当前研究中，数据稀疏度高算法效率低，以及算法推荐精确度不高这2个问题，本文提出一种基于图模型和K近邻(K-nearest neighbor,KNN)模型的GK-CF算法.为了解决社会网络推荐中数据过于稀疏的问题，本算法将原有的评分数据使用加权无向图的方式进行数据建模，图节点和边表示用户、项目及其之间的关系，以利用图的拓扑性质和基本的图算法.同时，基于文献[1]的研究发现用户更容易接受来自有相似项目购买偏好的用户的推荐，在本文中我们采用改进的K近邻算法结合无向有权图中消息的传播，以及改进的相似度计算模型来进行相似用户的筛选，使所得到的相似用户更加精准.进一步地，算法通过图的最短路径算法来进行带评分项目的快速定位和筛选，也降低了计算的复杂性.最后利用并行图框架对算法进行了优化，使得本文提出的方法具有较好的实时性.

1 相关工作

2006年，美国著名的DVD租赁网络Netflix为了推动推荐系统中评分预测问题的研究，举行了Netflix Prize比赛，伴随着大量研究人员的深入研究推动了学术界对推荐系统的研究.近年来社会网络快速兴起使得推荐系统的发展有了新的动力和时机.社会网络可以很好地模拟现实社会，学术界和工业界对于如何利用社会网络给用户进行个性化推荐及对社会化推荐过程的建模方法进行了广泛的研究.

作为推荐算法的典型代表，协同过滤算法近年来受到工业界和学术界的广泛关注.协同过滤算法不需要预先获取用户或项目的特征，仅依赖于用户的历史兴趣显式或隐式反馈对用户兴趣建模，再根据所建模型为用户进行推荐.在协同过滤算法中，显式反馈指的是用户曾经对项目有过的历史评分或者报告，隐式反馈指的是用户群的历史购买信息、浏览信息、搜索模式和鼠标停留信息等.以基于用户的协同过滤算法为例，其主要关注点是根据相似用户曾有的对项目的历史评分预测出目标用户u对项目i的兴趣度.其中，用户之间相似度的计算有很多种方法，比较常见和普遍使用的就是根据2个用户对共同关注过的项目的历史评分来进行皮尔斯相似度和余弦相似度[1]的计算.

学术界在余弦函数和皮尔斯函数的基础上已经提出了大量的提高算法准确度和表现的算法，如用户倒排评分、实例扩展[3]和主流加权预测[4].Park等人[5]提出了一种基于KNN图的协同过滤算法.KNN图的构建基于对项目的贪婪过滤，从而确定与每个项目最相似的前K′个项目列表.然后从当前用户未评分项目中筛选出其K′个项目与目标用户曾经评分项目集合的交集为K的项目，再计算目标用户对其的评分.在降低计算复杂度的同时保持了算法的精度.但算法的主要关注点放在用K近邻图来提高寻找相似用户的效率上，缩小了需要计算的未评分项目的范围，而且此算法不能预测目标用户对所有未评分项目的兴趣度.Das等人[6]利用二叉树剖分技术提出了一种将用户所在区域分解后仅利用与用户相关的特殊区域的数据为当前用户进行推荐的推荐算法，从而降低了计算的复杂度.Liu等人[7]提出了一种结合了用户评分的全局偏好信息和每对用户共同评分的上下文信息的启发式相似度计算模型，来提高评分预测的准确性.Xiang等人[8]引入时间窗口信息区分用户不同时间段的行为，提高评分预测的准确性.Ding等人[9]根据项目加入系统的时间引入相应的衰减因子提高推荐的准确性.Koren[10]利用时序图对用户的长期兴趣和短期兴趣进行区分，旨在更准确地定义用户当前兴趣，提高推荐准确性.孙光福等人[11]通过衡量用户之间的关系寻找相似的邻居用户，提出了一种对用户间的时序行为进行建模的方法并将基于该方法发现的邻居集合成功融入到基于概率矩阵分解的协同过滤推荐算法中，提升推荐精度.Matook等人[12]提出了一种结合了熟人之间的推荐和历史评分的推荐算法.Jia等人[13]提出了一种基于双层邻居选取策略的协同过滤推荐算法.Qin等人[14]提出一种融合信任和用户情感偏好的协同过滤算法.此外，为了提高推荐的准确性，Alami等人[15]提出了一种结合2种启发式方法进行相似用户选择及使用矩阵分解的方法发现相似用户或项目的潜在特征的混合协同过滤算法.Santos[16]提出一种将心理模型理论、积极心理学中的共同临时想法与传统的协同过滤算法结合的基于用户好奇心的混合推荐算法.

在基于图的模型中，用户与项目或者用户与用户或者项目与项目之间的关系往往是通过有向权图或者无向权图的方式来表示.通常情况下，图中的节点表示用户或者项目，图中的边被赋予了权值，用来表示用户间和项目间的相似度或者用户对项目的评分.在这些模型中，标准的方法只是利用与用户节点或者项目节点有边相连的节点来预测用户对于项目的评分.例如，通过统计用户节点和项目节点之间的距离来直接估计用户对项目的评分[17-18].在一些文献中[19-21]，目标项目节点或者用户节点往往也通过沿着图中的边对其消息进行广播来影响那些未与其直接连接的节点.

随着云计算时代的到来，Zhu等人[22]提出了一种适用于云计算分布式处理环境下基于协同过滤的个性化推荐机制RAC.

不断增长的数据规模也驱动了分布式并行图框架系统的出现[23-24]，这些系统可以优化数据在集群环境中的布局，并将复杂的迭代算法在有数百亿的顶点和边的图上进行分布执行.在并行图方式下的图算法的迭代效率要比普通的数据并行系统下的执行效率有数量级的提高[23].

2 评分数据表示及系统建模

2.1 评分数据描述

用u表示用户，p表示项目.用户历史评分记录中的用户集合用U={u1,u2,…,un}表示，项目集合用P={p1,p2,…,pm}表示，则用户历史评分记录可以用一个n×m的矩阵R表示，矩阵中的每一个元素rij表示用户ui对项目pj的已有评价分数，且i∈1,2,…,n，j∈1,2,…,m.如果用户集合中的某个用户ui对项目集合中的项目pj尚未有过评分，则在R评分矩阵中与其对应的矩阵元素rij为空，R评分矩阵为

其中，评分矩阵R中元素存在已知值和空值，已知值表示当前行所代表的用户曾经对当前列所代表的项目有过历史评分，空值表示当前行所代表的用户尚未关注当前列所代表的项目或者还未给项目做过评分.推荐算法的工作就是基于R中已有的评分值和其他相关信息对矩阵R中的空值进行预测.

2.2 基于无向有权图的数据表示及系统建模

本文中，我们引入图结构来对用户项目历史评分数据进行建模，基于并行化图模型的推荐系统框架如图1所示：

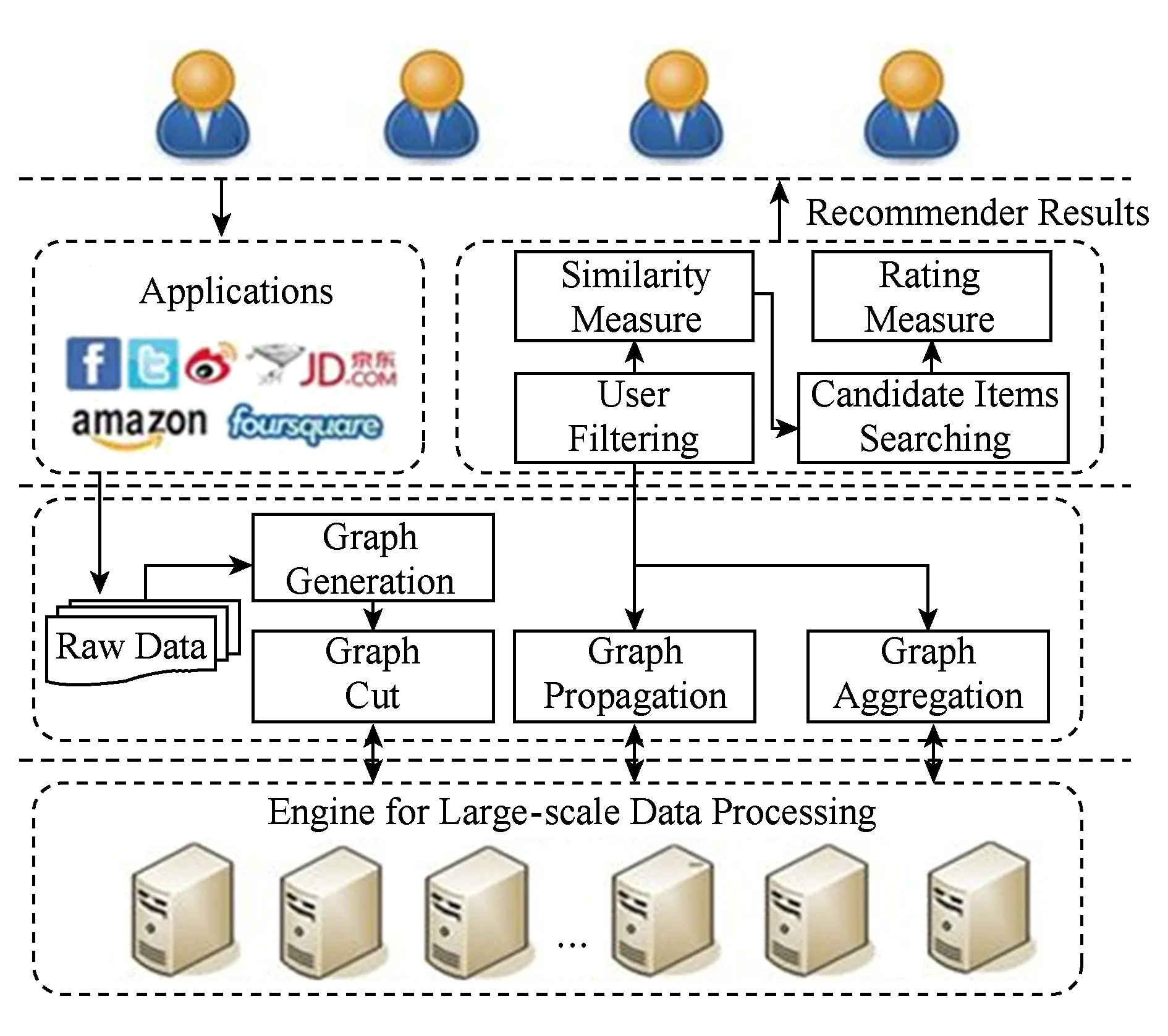
Fig. 1 Recommendation system architecture based on parallel graph framework图1 基于并行图模型的推荐系统架构

图1中，最底层是支持大规模数据处理的并行集群环境，通过分布式处理引擎支持流式计算和分布式存储.用户在参与社会化网络活动中形成的各种数据，通过图的生成、图的分割加载到底层的集群环境中，通过图的消息传播和汇聚及基于图的计算，可以对基于图的用户数据做进一步处理，包括用户过滤、用户相似度计算、确定候选项目以及对项目进行评分.最终将用户可能感兴趣的结果推荐给用户.

本文中，我们用无向有权图的方式对原始的评分矩阵进行建模，假设用图G表示用户评分的历史记录.G=(V,E).其中，V={v1,v2,…,vn,vn+1,vn+2,…,vn+m}，对应上文所提用户列表U和项目列表P的并集.其中v1～vn代表用户列表U中的用户u1～un;vn+1～vn+m代表项目列表P中的项目p1～pm.E代表图中边的集合，〈vi,vj〉∈E(i=1,2,…,n;j=n+1,n+2,…,n+m)代表用户vi曾经对vj有过历史评分，历史评分用来表示边的权值.图G如图2所示.则给用户ui推荐项目的问题可以定义为：在当前的无向有权图中，预测从用户顶点vi到与之没有边相连的某一项目顶点vj之间在图上的相关性.

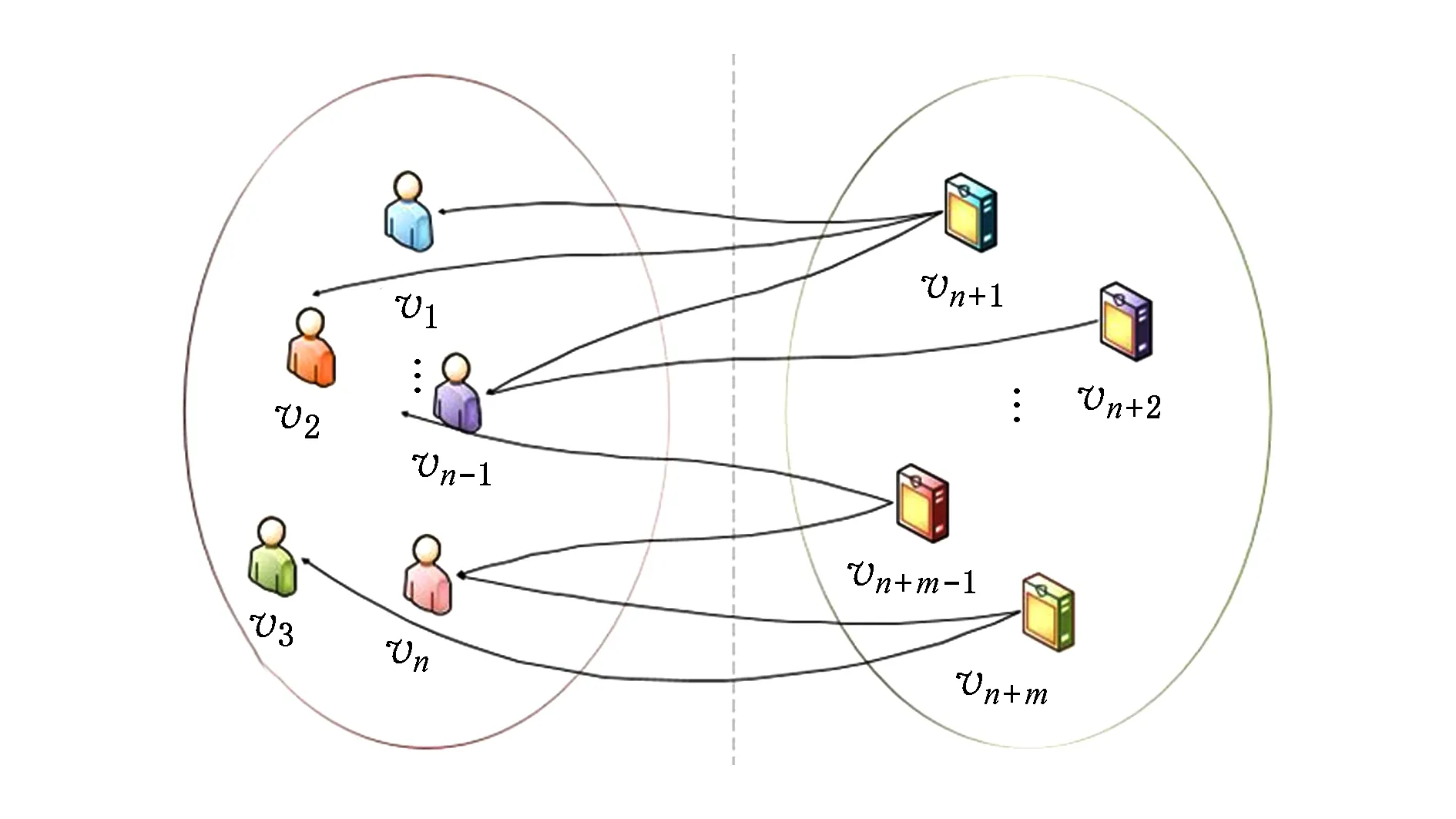
Fig. 2 The undigraph with weight based on the users- items historical ratings图2 用户-项目历史评分无向有权图

在这里给出基于图的评分数据模型的几个定义：

定义1. 目标顶点的2-度关联顶点.目标顶点vi的2-度关系顶点可以表示为集合：

{vj|〈vi,vj〉∉E∧(∃k)〈vi,vk〉∈E∧〈vk,vj〉∈E}，

即从图中该目标顶点vi出发，若存在1个中间节点vk，经过2条不重复边〈vi,vk〉以及〈vk,vj〉能够到达的顶点vj为目标顶点vi的2-度关联顶点.

定理1. 若以用户顶点为目标顶点，则其2-度关联顶点一定是用户顶点.因为本文针对的用户-项目历史评分是二部图结构，所有的边都代表某用户对某项目的评分，用户之间或项目之间不存在边.

证明略.

定义2. 用户的n-度关联项目.若从图中某一用户顶点vi出发，沿图中的边能够到达的项目顶点，称其为用户vi的关联项目，n表示从vi到达关联项目经过的边数.

定义3. 用户与关联项目的最短路径.若e1,e2,…,en∈E,其中，ei是关联于节点vi-1，vi的边，交替序列v0e1v1e2…envn称为联接v0到vn的路.边的数目n称作路的长度.若一条路中所有的节点v0,v1,…,vn均不相同，称作通路.从图中某一用户顶点vi出发到其关联项目vj存在多条通路，则从节点vi到节点vj路径中边数之和称为vi到vj的路径长度，长度最小的路径称为vi到vj的最短路径.

3 基于图和改进KNN的协同过滤算法GK-CF

在传统K近邻算法中，对每个目标用户uactive进行相似度计算时，都是对其计算与系统中所有剩余用户的相似度，使得计算量较大且复杂度高，或者由于相似用户的过滤过于随机使得推荐的精确度不高.

为了选出K个相似用户，传统的用户近邻模型直接通过皮尔斯公式和余弦公式来计算2个用户之间的临近程度.

本文对上述方法进行了改进，主要解决2个问题：

1)K个相似用户的选取问题；

2) 相似好友用户与目标用户uactive之间的相似度计算问题.

3.1 基于图的相似用户选取

文献[1]指出相比传统的基于评分的推荐，用户更容易接受来自有相似项目购买偏好的用户的推荐，因此本文在传统协同过滤算法的基础上，结合共同评分的上下文信息，在计算用户相似度之前，先进行目标用户uactive的相似用户筛选，仅考虑那些曾经与目标用户uactive有过共同选择和评分的用户，将其看作目标用户uactive的相似用户组，然后在目标用户uactive与其相似用户组间计算相似度.

按照2.2节前述基于图模型的定义1，与目标用户uactive有共同选择和评分的用户即为2-度关联用户，因此，筛选相似用户问题可以描述为求目标顶点的2-度关联顶点问题.

为了确定目标用户uactive的2-度关联用户，本文提出图的消息传播和聚合方法GraPA.

在GraPA方法中，图中的顶点有3种状态：1)未激活状态，记为S0；2)被消息激活对消息进行广播的状态，记为S1；3)收到消息后对消息进行合并的状态，记为S2.图中每一个顶点vi维护的消息可表示为vList=(vidi，Li)，其中vidi表示顶点vi的ID，Li表示在传播过程中到达顶点vi的其他顶点ID的集合，初始化为Li=(vidi).全图顶点按照离散的等间隔时间序列在3个状态间进行状态转换，完成消息的传播和聚合.图的信息传播和聚合的方法GraPA流程如算法1所示：

算法1. 基于时间步序列的图信息传播和聚合方法GraPA.

输入: 无向图G=(V,E)；

输出: 无向图G中所有顶点的消息列表List[(vid,Li)].

① 初始时刻，将图中的所有顶点的状态初始化为S0.

② 在时间步T=2n-1，所有顶点均作为发布消息的源节点，沿着以当前广播消息顶点vi为源顶点的边e〈vi，vj〉广播vi顶点的Li至顶点vj，这是图的消息传播.

③ 在时间步T=2n，所有顶点将时间步T=2n-1时收到的不同源顶点广播来的顶点，如Lj,Lp,…,Lk合并起来，同时将合并后的集合L=Lj∪Lp∪…∪Lk作为顶点vi的更新后的Li.这是图的消息聚合.

从图的初始时刻开始，在经过1轮2个时间步后，每个用户顶点所维护的Li即为该用户的2-度关系用户.

3.2 用户相似度计算

在筛选出用户的2-度关联用户后，接着计算2-度关联用户与目标用户uactive之间的相似度.

如果用I来表示2用户u和v曾经共同给过评分的项目集合，则传统的皮尔斯公式计算用户之间的相似度为

(1)

传统的皮尔斯公式仅考虑2用户曾经有过共同评分的项目，对于一方用户曾经做过评分而另一方用户尚未关注的项目不加考虑.但是这种拥有共同评分的项目数较少，使得用于计算2用户之间相似度的数据过少，在一定程度上降低了用于推荐预测的信息量.因此，在本文中，我们考虑2用户间一方有评分而另一方尚未评分的项目，假设用Iuv=Iu-Iv表示用户u曾经有过评分而用户v尚未评分的项目，并将用户v对这一部分项目的评分统一赋值为常量C.同理用Ivu=Iv-Iu表示用户v曾经有过评分而用户u尚未评分的项目，同时将用户u对这一部分项目的评分也统一赋值为常量C.将Iuv和Ivu这2个集合中的项目评分加入计算，则式(1)中，计算用户评分与此用户的评分均值的偏离度的平方和扩展为

(2)

式(1)中，除了计算I中项目涉及到的2个用户评分与对应用户的评分均值偏离度的乘积和

(3)

还将考虑Iuv和Ivu这2个集合中的项目，将式(3)扩展为

(4)

从而保证2用户有足够的评分项目信息量用于计算用户之间的相似度.

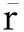
(5)

(6)

综上，本文提出用户相似度的计算方法：

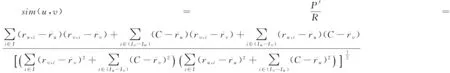
(7)

3.3 基于图最短路径的可推荐项目数计算

对于无向图G=(V,E)中的一条路径是指1个顶点序列P=v1v2…vk,其中每一对相邻的顶点vi和vi+1之间都有1条边,P也称为从v1到vk的一条路径.按照2.2节定义2和定义3，在一个无向图中的节点vi到节点vi+1的最短路径指的是从节点vi到节点vi+1路径长度之和最小的路径.

通过最短路径寻找符合条件的项目的过程我们通过图的消息传播方式实现，此算法归结为在无向图G的拓扑节点中迭代执行特定的算法，shortPA算法流程如算法2所示：

算法2. 基于图消息传播的ShortPA算法.

输入: 无向图G=(V,E)、目标顶点的ID:TargetID；

输出: 无向图G中所有非目标顶点的顶点ID-属性列表List[(VID,Vattribute)].

① forV-*初始化*-

② ifVid==TargetIDthen

changeVattr(Vid,0);

③ elsechangeVattr(Vid,∞);

④ end if

⑤ end for -*初始化各顶点的属性为到目标顶点的距离，也即定义各非目标顶点到目标顶点的距离为无穷大，目标顶点到自身的距离为0*-

⑥ repeat；

⑦ begin Phase 1：并行化； -*图中每条边上的源节点沿着与其相连的边向其目标顶点发送消息，当源顶点自身的距离属性值加1小于目标顶点的属性值时，设定源顶点的属性值加1为当前要发送的消息，否则，设定要发送的消息值为空*-

⑧ ifsrcVattr+1

⑨ elsesentMessage(dstID,positiveInfitility)；

⑩ end if

由于评分数据图的规模性，评分数据图会进行分割得到评分数据子图，为了保证对数据的并行处理，在算法2中，阶段1、阶段2及阶段3均为可并行对各评分数据子图进行分别处理的设计.

基于用户的协同过滤推荐中用户u对项目i的兴趣度评分是通过综合用户u的其他相似用户对项目i的评分而得到的：

ru,i=aggrsu∈Srsu,i，

(8)

其中，S表示用户u的相似用户中曾经给项目i做过评分的用户的集合.为提高预测评分的精确度，在具体的算法[1]中，用户u对项目i的评分ru,i通过式(9)进行计算：

(9)

其中，k是正则化因子，通常通过

求得，其中Isu代表用户su曾经给过评分的项目的集合.

3.4 GK-CF算法及其并行化设计

本文提出的基于图模型和改进K近邻的协同过滤算法GK-CF，算法伪代码描述如算法3所示：

算法3. 基于图模型和改进K近邻的协同过滤GK-CF算法.

输入: 用户-项目历史评分数据ru,i；

输出: 推荐项目列表List[Iid].

① 初始化:G:(V,E)←graphBuild(ru,i)；

-*G为无向有权图，V={v1,v2,…,vn,vn+1,vn+2,…,vn+m},对应上文所提用户列表U和项目列表P的并集.其中的v1～vn代表用户列表U中的用户u1～un.vn+1～vn+m代表项目列表P中的项目p1～pm.E代表图中边的集合.E〈vi,vj〉∈E代表vi所代表的用户ui曾经对vj所代表的项目pj有过历史评分*-

②U1={v1,vi,…,vn}←GraPA(G)； -*筛选出目标用户uactive的2-度关系用户*-

③unSortPearson={(v1,Pv1),(vi，Pvi),…,(vn，Pvn)}←improvedPearson(U1)； -*计算用户集U1与目标用户uactive之间的相似度*-

④U1′←SortByPearsonValueAndTakeTopK(unSortPearson,K)； -*根据其与目标用户uactive之间的相似度进行排序后选出其前K个用户作为目标用户uactive的相似用户集U1′*-

⑤I′={vm+1,vm+k,…,vm+n+1}←ShortPA(G,TargetID)； -*根据ShortPA算法筛选出符合条件的项目集*-

⑥unSortItemAttractive={(vm+1，Avm+1)，(vm+k，Avm+k+1),…,(vm+n+1，Avm+n+1)}←formulation(I′)； -*根据式(9)计算出目标用户uactive对可推荐项目集I′={vm+1,vm+k,…,vm+n+1}中项目的兴趣度*-

⑦List[Iid]={vm+1，vm+p,…,vm+n-2}←SortByAttractiveValueAndTakeTopN(unSortItemAttractive，K)； -*选择预测值前top-N的项目作为推荐项目推荐给用户*-

⑧ returnList[Iid].

GK-CF算法的输入为根据用户-项目历史评分文件生成的基于并行计算框架Spark的弹性分布式数据集(resilient distributed dataset, RDD).RDD是不可变的带分区的记录集合，也是Spark中的编程模型，与并行计算框架Hadoop的MapReduce 2阶段提交任务，任务间相互等待高时延不同，Spark提供了RDD上的2类操作：RDD本身的转换(trans-formation)以及对RDD的动作(action).在Spark中，一段程序实际上就构造了一个由相互依赖的多个RDD组成的有向无环图(directed acyclic graph， DAG)，将这个有向无环图作为一个任务提交给Spark执行将完成在RDD上的各种操作.因此Spark任务之间不需要互相等待，对于迭代式数据处理性能好.并且Spark每次迭代的数据保存在内存中，使得Spark的性能相比Hadoop有很大的提升[23,25].

GK-CF算法中的每一步都进行了并行化设计，使得全图数据得以并行化处理.其中，算法3中的步骤②和步骤⑤分别对应算法1和算法2,算法3中的步骤③(计算用户集U1与目标用户uactive之间的相似度)和步骤⑥(根据式(9)计算出目标用户uactive对可推荐项目集I′={vm+1,vm+k,…,vm+n+1}中项目的兴趣度)是另外2个重要步骤，对其并行化设计说明如下：

步骤③中，为了并行计算目标用户uactive和其2-度关系用户U1间的相似度，将计算相似度任务划分为4个不同的子任务：

2) 通过对用户-项目历史评分RDD及用户平均评分RDD进行连接(join)，map操作求出目标用户uactive和其2-度关系用户集U1={v1,v2,…,vn}中每个用户vu的评分均值偏离度RDD及其评分均值偏离度平方和RDD；

3) 再通过map操作将评分均值偏离度RDD做键值对中的key-value值交换后通过join操作将与目标用户uactive相关的评分偏离度RDD和与其2-度关系用户集U1中用户相关的评分偏离度RDD的笛卡儿积求出后，通过map操作求出目标用户uactive与其对应的2-度关系用户的评分均值偏离度的乘积RDD；

4) 通过对评分均值偏离度的乘积RDD及评分偏离度平方和的一系列join及map操作后获取目标用户uactive及其2-度关系用户间的相似度RDD.

同理，步骤⑥中的任务也可以分为2个子任务：

1) 通过求和(sum)和map操作计算出式(9)中的正则化因子k；

2) 基于算法步骤③中计算出的目标用户uactive与其2-度关系用户间的评分偏离度RDD、相似度RDD、目标用户平均评分RDD以及步骤⑥中计算出的正则化因子k通过join、过滤(filter)、map等一系列操作完成用户u对项目i的评分ru,i.

3.5 算法复杂度分析

由于推荐算法涉及对海量数据的处理，除了推荐结果的准确性之外，算法本身的复杂度也是需要讨论的.本文提出的GK-CF算法通过建立图数据模型及子图分割，实现了对原始海量数据的分布式并行处理，对其时间复杂度Ttime和空间复杂度Tspace分析如下：根据算法3的描述，算法3的主要步骤是计算目标用户uactive的2-度好友集合(步骤②)、计算目标用户uactive与其2-度好友间的相似度(步骤③)、基于图的最短路径计算可推荐项目(步骤⑤)及计算目标用户uactive对可推荐项目的兴趣度(步骤⑥).

1) 在计算目标用户uactive的2-度好友集合过程中，根据算法1中图的消息传播和聚合算法GraPA，每个顶点均需向其邻居顶点发送1次消息，假设图中的顶点个数为N(N为用户-项目评分文件中用户U和项目数P之和)，边的条数为E，则按邻接表方式存储图的空间复杂度为O(N+E).1次消息传播和聚合的时间复杂度为O(N)，2-度好友通过前后2次的消息传播和聚合，时间复杂度仍然为O(N).众所周知，用户评分数据具有高稀疏性，通过无向有权图对其建模后得到稀疏图，不失一般性，1个稀疏图其边数和图中节点数的关系表现为E≤(Nlog·N)-2.由于在此步骤中图中的每一个顶点都要沿着它的邻边向它的邻居顶点进行1次消息传播，并在邻居顶点进行存储以完成聚合操作，因此需要在每个顶点开辟的额外存储空间为2E≤Nlog·N.因此，此步骤中的空间复杂度为O(Nlog·N).

2) 在计算目标用户uactive与其2-度好友间的相似度时，其时间复杂度主要表现为RDD进行1次map操作的时间，也即对图中代表目标用户uactive的2-度好友的顶点的属性值进行1次变换修改操作的时间，因此，时间复杂度为O(N).在计算过程中需要将顶点数据的RDD存储在内存中，RDD通常以〈目标用户，2-度好友用户，相关value〉的方式存在，则此步骤的空间复杂度为O(N).

3) 在基于图的最短路径计算可推荐项目中，由于寻找最短路径需要进行3次消息传播，因此此步骤的时间复杂度为O(N)，空间复杂度为O(Nlog·N).

① http:--grouplens.org-datasets-movielens-

4) 在计算目标用户uactive对可推荐项目的兴趣度中，此计算过程同样需要将顶点的RDD以〈目标用户，可推荐项目，兴趣度〉形式存在内存中，其空间复杂度为O(N).此步骤时间复杂度与计算目标用户uactive与其2-度好友间相似度的时间复杂度一样为O(N).

综合分析得出，GK-CF算法的时间复杂度为O(N),空间复杂度为O(Nlog·N+E).由于算法的每一步均为并行执行，在给定集群环境拥有多台处理器数目的情况下，算法能够在更短的时空范围内完成计算.

通过具体的算法实现，对于同样的社会网络标准数据集MovieLens①，采用并行化方法设计实现的GK-CF算法在4.1节的实验环境下运行效率为3.33·s，而串行方式下该算法的运行效率为31.53·s.本文提出的算法在6个节点的并行平台上的运行效率较串行方式实现下的运行效率高出10倍.

上述2种算法的执行时间结果记录如表1所示.本文同时以Wilcoxon秩和检验方法检验采用并行化方法设计实现的GK-CF算法较之串行方式的实现效率是否有显著提升.

Table 1 The Descriptive Statistics of the Operation Efficiency of GK-CF and Serialized GK-CF

表1 GK-CF及其串行方式实现的运行时间的描述性统计

从表1中可以看出，GK-CF算法通过并行化的实现，其运行效率远高于串行方法.基于Wilcoxon秩和检验方法对表1中数据进行了分析.

Wilcoxon秩和检验是一种非参数统计方法[26]，综合了t_test和阈值误判方法(threshold number of misclassification，TNOM)的良好特性，克服了t_test对于噪音敏感和TNOM会丢失数据中信息的缺点[27].Wilcoxon秩和检验法在检验样本时，首先在符号检验的基础上计算样本的正、负号秩及其样本秩的总和w及样本的统计量概率p.如果样本的统计量z的统计量概率p接近于0，则2配对样本存在着显著性的差异.其中，样本统计量z计算为

z=[w-n1(n1+n2+1)-2]-

[n1n2(n1+n2+1)-12]1-2，

(10)

其中，n1为第1个样本集的样本容量，n2为第2个样本集的样本容量，w为第1个样本集样本的秩和.

检验结果如表2所示：

Table 2 The Wilcoxon Rank SumTest表2 Wilcoxon秩和检验

该结果显示Wilcoxon统计量w和z皆拒绝GK-CF和其串行方式的算法运行效率相等的零假设.且样本的统计量z的统计量概率p接近于0，2配对样本存在显著性差异，该检验表明，并行化设计实现的GK-CF较其串行方式的实现，在运行效率上有显著提升.

4 实验及结果分析

本节通过实验继续对本文提出算法的推荐效果进行验证，讨论了选取不同的用户数和项目数对推荐结果的影响.并将本文提出的算法GK-CF同其他算法在真实的物理集群环境下进行了实现及对比.

4.1 数据集及实验环境

实验环境由6台服务器组成云平台集群，服务器运行的是Ubuntu14.04 64位系统，集群管理平台为Spark1.1.0，每台服务器节点包括一个4核CPU和8·GB内存.集群由1台服务器作为Master节点，5台作为计算节点.实验中GK-CF算法与所有参与对比的算法均在Spark平台上进行了并行化实现.

实验采用大规模社会网络标准数据集MovieLens①来验证本文所提出的GK-CF算法能够更好地进行社会网络应用中对项目的推荐.

① http:--grouplens.org-datasets-movielens-

4.2 评价指标和实验参数

为了使本文提出的算法能够取得较好的推荐效果，我们分别对相似用户数量和项目数量的选取进行了实验.分别考虑了预测的均方根误差(rmse)、准确率(precision)以及召回率(recall)三个评价指标.

(11)

令R(u)是根据用户在训练集上的行为为用户做出的推荐列表，而T(u)是用户在测试集上的行为列表，则推荐结果的准确率(precision)定义为

(12)

推荐结果的召回率(recall)定义为

(13)

表3对推荐的项目数不做限制的情况下，选取不同数量的相似用户的实验结果.通过表3可以看出，在重点考虑rmse的前提下，当用户数取100时，能够取得较好的rmse和recall，但precision略低.

Table 3 The Similar Users Number Choose Experiment表3 相似用户数选取

Table 4 The Candidate Items Choose Experiment表4 候选项目数选取

1)rmse

评分预测的预测准确度一般通过rmse计算.

本文对4种算法进行了对比实验，分别是：基于用户的协同过滤算法(collaborative filtering algori-thm, CF)、基于评分数据矩阵及本文提出的改进KNN算法实现的K-CF算法、基于交替最小二乘的协同过滤算法(alternating least squares-collaborative filtering algorithm, ALS-CF)以及基于图模型和改进KNN的GK-CF算法.在MovieLens①不同大小的数据集上分别运行上述算法.结果如图3所示，GK-CF算法的rmse值远低于基准CF算法、K-CF算法及ALS-CF，能够达到0.89，比ALS-CF低8%.说明本文提出的算法在评分预测的准确度上是优于其他3种算法的.

Fig. 3 The rmse comparison of four algorithms图3 4种算法的rmse对比

2)precision和recall

推荐结果准确率定义为推荐算法正确判定用户对一个项目是否喜欢的比例.因此，当用户只有二元选择时，使用precision，recall指标来衡量推荐质量，比rmse更直观.

① http:--grouplens.org-datasets-movielens-

② http:--webscope.sandbox.yahoo.com-catalog.php?datatype=r&did=3

本实验除了前述4种算法CF，K-CF，ALS-CF，GK-CF，进一步加入了基于图的随机游走的算法(实验中简称RW算法)参与对比.各算法在MovieLens①数据集上运行的precision和recall的实验结果分别如图4、图5所示.从图4可以看到，GK-CF的precision与ALS-CF相当，相对于其他3种方法优势较为明显，比基准CF算法precision提高25%.图5中，GK-CF的recall相对于基准CF算法、ALS-CF算法，分别提高25%，14%.

Fig. 4 The precision comparison of five algorithms图4 5种算法的precision对比

Fig. 5 The recall comparison of five algorithms图5 5种算法的recall对比

本文也通过不同的标准数据集对GK-CF算法与其他算法进行了对比实验.表5是GK-CF算法与ALS-CF算法在标准数据集Yahoo!Music 1·MB②上进行的对比实验.实验结果表明，GK-CF算法的recall仍高于ALS-CF算法的recall，并且GK-CF算法的precision比ALS-CF算法的precision提高了3%.

3) 算法运行效率

我们考察了在同样节点规模的情况下，不同算法的运行效率.基准CF算法在前述实验中牺牲precision，recall，rmse的情况下，运行效率较高.GK-CF与ALS-CF运行效率相当，说明，GK-CF在取得较好的rmse，precision，recall的情况下，并未以牺牲算法效率为代价.其实验结果如图6所示.

Table 5 TherecallandprecisionComparisons Between GK-CF and ALS-CF

表5 GK-CF 与ALS-CF算法的召回率及准确率对比 %

Fig. 6 The runtime comparison of five algorithms图6 5种算法运行时间对比

GK-CF与ALS-CF在Yahoo!Music 1·MB②数据集上的算法运行效率如表6所示.GK-CF算法较ALS-CF算法运行效率高.

Table 6 The Algorithm Runtime Comparisons Between GK-CF and ALS-CF表6 GK-CF 与ALS-CF算法的运行时间对比 s

4) 加速比

在真实的物理集群环境下，节点的规模与并行算法的执行效率是相关的，本文通过GK-CF，RW及ALS-CF算法的加速比实验，对算法在节点规模上的可扩展性进行了分析.如图7在MovieLens①的1·MB规模数据集上，算法的加速效率较为明显，当集群规模从1个节点变换到5个节点时，本文提出的GK-CF算法效率有近3倍的提升，与ALS-CF算法相当.说明本文提出的算法随着节点规模的扩展有良好的可扩展性.RW算法的效率虽然比GK-CF和ALS-CF的算法效率低近15倍且当其运行于单个节点时算法效率过低，但其加速比有近7倍的提升，也说明对于基于图模型的算法求解，适合于通过并行平台来加速执行效率.

Fig. 7 The speedup experiment of three algorithms图7 3种算法加速比实验

5 总 结

现有的个性化推荐系统不仅需要处理海量、实时的数据，而且还要响应用户多样化的服务请求，如亚马逊的个性化书籍推荐和YouTube的个性化视频推荐.然而大多数推荐算法存在算法精确度不高、运行效率低等问题，导致推荐质量受限.本文提出了一种基于图模型和改进KNN模型的GK-CF算法，并对算法进行了并行化的实现.通过建立图数据模型及子图分割，实现了对原始海量数据的分布式并行处理.利用图拓扑结构及沿图路径信息传播和聚合的方式提出了改进的KNN算法，用于对每个目标用户的相似用户筛选，并通过改进的皮尔斯公式处理由于用户过多带来相似度计算误差，再利用图的最短路径算法对目标用户的可推荐项目集合进行快速定位，最后根据目标用户对项目的评分选出最终给用户推荐的项目.我们在真实的集群环境下，利用标准数据集验证了基于并行图的GK-CF推荐算法的有效性.实验结果表明，相对于基准CF算法、基于模型的ALS-CF算法以及基于图结构的随机游走RW算法，GK-CF算法有较好的rmse，precision，recall.同时并未以牺牲算法效率为代价.本文也通过算法复杂度分析、GK-CF算法的串行化和并行化的算法运行效率对比实验和Wilcoxon秩和检验验证了GK-CF由于其并行化设计实现具有较好的高效性，在未来的可扩展集群上也具有较好的算法可扩展性.

[1]Adomavicius G, Tuzhilin A. Toward the next generation of the recommender systems: A survey of the state-of-the-art and possible extensions[J]. IEEE Trans on Knowledge and Data Engineering, 2005, 17(6): 734-749

[2]Koren Y. Factorzation meets the neighborhood: A multifaceted collaborative filtering model[C] --Proc of the 14th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2008: 426-434

[3]Breese J S, Heckerman D, Kadie C. Empirical analysis of predictive algorithms for collaborative flitering[C] --Proc of the 14th Conf on Uncertainty in Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 1998: 43-52

[4]Delgado J, Ishii N. Memory-based weighted-majority prediction for recommender systems[C] --Proc of the ACM SIGIR’99 Workshop Recommender Systems: Algorithms and Evaluation. New York: ACM, 1999

[5]Park Y, Park S, Jung W. Reversed CF: A fast collaborative filtering algorithm using aK-nearest neighbor graph[J]. Expert Systems with Applications, 2015, 42(8): 4022-4028

[6]Das J, Aman A K, Gupta P, et al. Scalable hierarchical collaborative filtering using BSP trees[C] -- Proc of the Int Conf on Computational Advancement in Communication Circuits and Systems. Berlin: Springer, 2015: 269-278

[7]Liu Haifeng, Hu Zheng, Mian Ahmad, et al. A new user similarity model to improve the accuracy of collaborative filtering[J]. Knowledge-Based Systems, 2014, 56(1): 156-166

[8]Xiang Liang, Yuan Quan, Zhao Shiwan, et al. Temporal recommendation on graphs via long-and short-term preference fushion[C] --Proc of the 16th ACM Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 723-731

[9]Ding Yi, Li Xue. Time weight collaborative filtering[C] --Proc of the 14th ACM Int Conf on Information and Knowledge Management, New York: ACM, 2005: 485-492

[10]Koren Y. Collaborative filtering with temporal dynamics[J]. Communications of the ACM, 2010, 53(4): 89-97

[11]Sun Guangfu, Wu Le, Liu Hong, el al. Recommendations based on collaborative filtering by exploiting sequential behaviors[J]. Journal of Software, 2013, 24(11): 2721-2733 (in Chinese )(孙光福, 吴乐, 刘洪, 等. 基于时序行为的协同过滤推荐算法[J]. 软件学报, 2013, 24(11): 2721-2733)

[12]Matook S, Brown S A, Rolf J. Forming an intention to act on recommendations given via online social networks[J]. European Journal of Information Systems, 2015, 24(1): 76-92

[13]Jia Dongyan, Zhang Fuzhi. A collaborative filtering recommendation algorithm based on double neighbor choosing strategy[J]. Journal of Computer Research and Development, 2013, 50(5): 1076-1084 (in Chinese )(贾冬艳, 张付志. 基于双重邻居选取策略的协同过滤推荐算法[J]. 计算机研究与发展, 2013, 50(5): 1076-1084)

[14]Qin Jiwei, Zheng Qinghua, Tian Feng. Collaborative filtering algorithms integrating trust and preference of user’s emotion[J]. Journal of Software, 2013, 24(Suppl 2): 61-72 (in Chinese)(秦继伟, 郑庆华, 田峰. 一种融合信任和用户情感偏好的协同过滤算法[J]. 软件学报, 2013, 24(增刊2): 61-72)

[15]Alami Y, Nfaoui E, Beqqali O. Toward an effective hybrid collaborative filtering: A new approach based on matrix factorization and heuristic-based neighborhood[C] --Proc of the Intelligent Systems and Computer Vision(ISCV). Piscataway, NJ: IEEE, 2015: 51-58

[16]Santos A. A hybird recommendation system based on human curiosity[C] --Proc of the 9th ACM Conf on Recommender Systems. New York: ACM, 2015: 367-370

[17]Fouss F, Pirotte A, Renders J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Trans on Knowledge and Data Engineering, 2007, 19(3): 355-369

[18]Huang Zan, Chen Hsinchun, Zeng Daniel. Applying associative retrieval techniques to alleviate the sparsity problem in collaborative filtering[J]. ACM Trans on Information System, 2004, 22(1): 116-142

[19]Aggarwal C C, Wolf J L, Wu Kun-Lung, et al. Horting hatches an egg: A new graph-theoretic approach to collaborative filtering[C] --Proc of the 5th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 1999: 201-212

[20]Onuma K, Tong H, Faloutsos C. TANGENT: A novel, surprise me, recommendation algorithm[C] --Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 657-666

[21]Xiang Liang, Yuan Quan, Zhao Shiwan, et al. Temporal recommendation on graphs via long-and short-term preference fusion[C] --Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 723-732

[22]Zhu Xia, Song Aibo, Dong Fang, et al. A collaborative filtering recommendation mechanism for cloud computing[J]. Journal of Computer Research and Development, 2014, 51(10): 2255-2269 (in Chinese )(朱夏, 宋爱波, 东方, 等. 云计算环境下基于协同过滤的个性化推荐机制[J]. 计算机研究与发展, 2014, 51(10): 2255-2269)

[23]Xin R S, Crankshaw D, Dave A, et al. GraphX unifying data-parallel and graph-parallel analytics[DB-OL]. Computer Science Databases. 2014[2016-04-29]. https:--arxiv.org-abs-1402.2394

[24]Quick L, Wilkinson P, Hardcastle D. Using pregel-like large scale graph processing frameworks for social network analysis[C] --Proc of 2012 IEEE-ACM Int Conf on Advances in Social Networks Analysis and Mining. Piscataway, NJ: IEEE, 2012: 457-463

[25]Zaharia M, Chowdhury M, Das T, et al. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing[C] --Proc of the 9th USENIX Conf on Networked System Design and Implementation. Berkeley, CA: USENIX Association, 2012: 15-28

[26]Deng lin, Pei Jian, Ma Jinwen, et al. A rank sum test method for informative gene discovery[C] --Proc of the 10th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2004: 410-419

[27]Xie Juanying, Gao Hongchao. Statistical correlation andk-means based distinguishable gene subset selection algorithms[J]. Journal of Software, 2014, 25(9): 2050-2075 (in Chinese)(谢娟英, 高红超. 基于统计相关性与K-Means的区分基因子集选择算法[J]. 软件学报, 2014, 25(9): 2050-2075)

Meng Huanyu, born in 1990. Master. Her main research interests include recommender system, location-based social networks.

Liu Zhen, born in 1977. PhD, associate professor. Member of CCF. Her main research interests include recommender system, location-based social networks, cloud and virtualization.

Wang Fang, born in 1977. Associate professor. Member of CCF. Her main research interests include future network architecture, mobile and internet.

Xu Jiadong, born in 1991. Master. His main research interests include recommender system, location-based social networks.

Zhang Guoqiang, born in 1980. PhD, associate professor. Senior member of CCF. His main research interests include future network architecture, network science.

An Efficient Collaborative Filtering Algorithm Based on Graph Model and ImprovedKNN

Meng Huanyu1, Liu Zhen1, Wang Fang2, Xu Jiadong1, and Zhang Guoqiang3

1(SchoolofComputerandInformationTechnology,BeijingJiaotongUniversity,Beijing100044)2(InformationTechnologyCenter,BeijingJiaotongUniversity,Beijing100044)3(SchoolofComputerScienceandTechnology,NanjingNormalUniversity,Nanjing210023)

With the rapid development of Internet, recommender system has been considered as a typical method to deal with the over-loading of Internet information. The recommender system can partially alleviate user’s difficulty on information filtering and discover valuable information for the active user. Collaborative filtering algorithm has the advantages of domain independence and supports users’ potential interests. For these reasons, collaborative filtering has been widely used. Because the user item rating matrix is sparse and in large-scale, recommender system is facing big challenges of precision and performance. This paper puts forward a GK-CF algorithm. By building a graph-based rating data model, the traditional collaborative filtering, graph algorithms and improvedKNN algorithm have been integrated. Through the message propagation in the graph and the improved user similarity calculation model, candidate similar users will be selected firstly before the calculation of users similarity. Based on the topology of bipartite graph, the GK-CF algorithm ensures the quick and precise location of the candidate items through the shortest path algorithm. Under the parallel graph framework, GK-CF algorithm has been parallelized design and implement. The experiments on real world clusters show that: compared with the traditional collaborative filtering algorithm, the GK-CF algorithm can better improve recommendation precision and the rating accuracy. The GK-CF algorithm also has good scalability and real-time performance.

collaborative filtering; social network; graph model;KNN; shortest path

2016-04-26；

2016-10-20

国家重点研发计划项目(2016YFB1200100)；国家自然科学基金项目(61202429,61572256)；中央高校基本科研业务费专项资金项目(2015JBM042)；江苏省自然科学基金项目(BK20141454) This work was supported by the National Key Research and Development Program of China (2016YFB1200100), the National Natural Science Foundation of China (61202429, 61572256), the Fundamental Research Funds for the Central Universities (2015JBM042), and the Natural Science Foundation of Jiangsu Province of China (BK20141454).

刘真(zhliu@bjtu.edu.cn)

TP181