一种巴氏系数改进相似度的协同过滤算法

武文琪 王建芳 张朋飞 刘永利

(河南理工大学计算机科学与技术学院 河南 焦作 454000)



一种巴氏系数改进相似度的协同过滤算法

武文琪 王建芳 张朋飞 刘永利

(河南理工大学计算机科学与技术学院 河南 焦作 454000)

针对传统协同过滤算法中评分数据稀疏性及所造成推荐质量不高的问题，提出一种巴氏系数(Bhattacharyya Coefficient)改进相似度的协同过滤算法。在基于近邻协同过滤算法基础上，首先利用Jaccard相似性来计算用户间的全局相似性；其次使用巴氏系数获得评分分布的整体规律，并结合Pearson相关系数来计算其局部相似性；最后融合全局相似性和局部相似性得到最终的相似度矩阵。实验结果表明，该算法在稀疏数据集上获得更好的推荐结果，有效地缓解了评分数据稀疏性问题，提高了推荐的准确度。

协同过滤 数据稀疏性 巴氏系数 相似度计算

0 引 言

推荐系统帮助人们成功解决信息过载问题[1]，并且在过去的几十年建立了电子商务的重要组成部分。推荐系统的首要任务是通过对大型项目空间的滤波为用户提供项目或产品的个性化推荐。推荐算法在电子商务、数字图书馆、电子媒体和在线广告等各种应用中发展，其中协同过滤算法在推荐系统中得到了广泛的应用[2]。

基于近邻的协同过滤作为协同过滤中重要的一类，其简单、直观、有效的特点被广泛应用于电影、音乐、图书等领域。其基本思想是采用一种相似性度量方法寻找最近邻居集合；然后通过对最近邻居集合的评分进行加权平均求和，从而产生推荐集[3]。相似性计算的准确性直接影响推荐质量，用户之间的相似性是基于两个用户对相同项目的评分(共同评分)，同样，项目之间的相似性是在对项目具有共同评分的用户基础上进行计算。但是，当数据极大稀疏无法保证足够的共同评分数据，传统的相似性计算方法其推荐效果不佳。即使没有一个共同用户，两个项目也可以是相似的；用户评价的项目不同，两个用户也可以是相似的，这些情况是传统的相似性方法没有考虑到的。因此，传统的相似性计算方法并不适合于稀疏数据(共同用户很少或者共同评价项目很少甚至没有)。

文献[4]在推荐系统中引入了用户相似度的概念，改善了社交网络中用户好友推荐的问题。文献[5]中提出了基于用户模糊相似度的协同过滤算法，分别建立年龄和评分的梯形模糊模型，将用户年龄和评分模糊化，进行相似度计算。文献[6]基于搜索引擎日志，提出了一种基于流行性和相似性相结合的查询推荐策略，为目标用户产生推荐词集合，改善推荐的多样性和流行性。文献[7]提出了一种结合Jaccard相似度和皮尔逊(Pearson)相关系数的改进相似性度量方法，在计算相似度时不但考虑共同评分还考虑共同评分的绝对数量，提供精确的评分预测。Bobadilla等提出了基于MSD(均方误差)的相似度度量方法；并在此基础上将评分数据结合上下文信息，提出Jaccard与MSD相结合的相似度来提高皮尔逊相关性的结果[8]。上述改进相似度计算方法在计算相似度时只考虑了相似性的全局信息，没有考虑其局部相似性；适用于数据集相对集中(存在共同评分)，没有共同评分时其推荐结果不佳，实际中用户评价的项目只是项目空间中的九牛一毛，其共同评分更少甚至没有。

针对上述问题，在基于近邻协同过滤算法的基础上，本文提出了一种利用巴氏系数改进相似度的协同过滤算法(BCCF)，通过改进相似度计算方法缓解数据稀疏性问题，以及数据稀疏导致无法计算相似度的问题。改进相似度计算重视用户的每一个评分，在计算用户之间相似性时，不仅考虑到用户评分之间的相似性，还结合Jaccard和Pearson方法的优点，利用巴氏系数来发现用户评分的分布规律。在Movielens数据集上的实验表明，BCCF算法在相对稀疏的数据集上的表现更好，有效改善评分数据稀疏性问题，提高预测评分的准确性。

1 相关工作

协同过滤算法的关键在于最近邻居集合的选择，推荐系统的性能直接依赖于目标用户(项目)邻居的选择，也就是依赖于用户(项目)之间相似度的度量，因而改进相似性计算方法成为提高推荐系统性能的有效途径之一[9]。协同过滤中常用的相似性度量方法：余弦相似性、调整余弦相似性、Pearson相关系数和Jaccard相似性等[10]，以基于用户的协同过滤算法为例。

(1) 余弦相似度

将用户的评分看作为一个向量，计算两个用户评分向量的夹角余弦值来衡量两个用户之间的相似度。

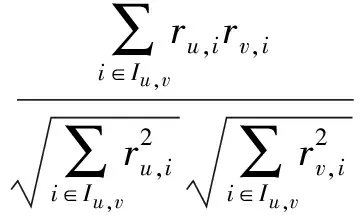
(1)

式(1)中Iu,v表示用户u和v的共同评分项目集，ru,i和rv,i分别表示用户u和用户v对项目i的评分。

如ru= (1,1)，rv= (5,5)，simcos(u,v)=1，尽管两个用户的评分差距很大(一个非常满意，一个非常不满意)，但两个用户的余弦相似度却为1。余弦相似性过于关注向量之间的夹角而忽视向量的长度(共同评分项数量)，且过于依赖两个用户的共同评分，这种方式对评分数值不敏感。

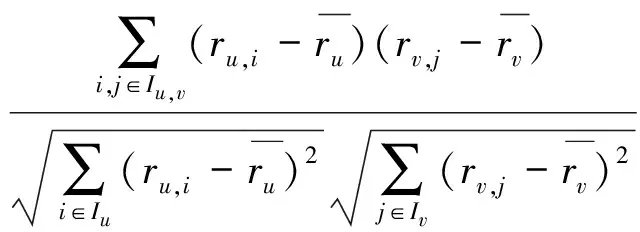
(2)

(3) Pearson相关系数

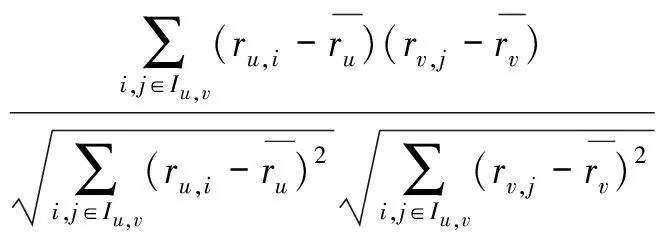
(3)

Pearson相关系数用来度量两个评分数据集合之间的线性关系，但对数值之间的差距不敏感。令ru=(1,1,3,3,2)，rv=(3,3,5,5,4)。simpear(u,v)=1。两组数据的差异明显，用户u对项目的评分都较低，而用户v对项目的评分都较高，很难看出两者之间有相关性，其计算结果与理论分析完全相反。Pearson相关系数考虑到用户评分的偏差，却忽略了评分的全局信息和用户共同评分的项目数，所以线性相关系数并不能很好地度量相似性。

(4) Jaccard相似度

(4)

其中Iu表示用户u评分的项目，Iv表示用户v评分的项目。Jaccard相似度与Pearson相关系数不同，Jaccard相似度仅考虑了两个用户的共同评分数，但未考虑绝对评分，从而影响用户相似度的准确性。

针对上述相似性计算方法中存在的缺陷，本文在基于近邻协同过滤算法的基础上，提出了一种利用巴氏距离改进相似性度量方法，充分利用用户的每一个评分，即使没有一个共同项目评分时，也可以计算两个用户之间的相似度。Jaccard相似度通过计算两个用户共同评分项目数的比重，能够在全局上衡量两个用户的相似度，以此作为全局相似度，Pearson相关系数考虑到用户评分偏差，并结合巴氏系数得到的评分整体规律，以此可以作为局部相似性，将全局和局部相似性进行融合作为两个用户之间最终的相似度值。

2 一种巴氏系数改进相似度的协同过滤算法

2.1 巴氏系数

巴氏系数是对两个评分数据向量的重叠近似计算，可用来对两个用户之间评分的相关性进行测量。已广泛应用于信号处理、模式识别研究领域。

在连续域两个密度分布p1(x)和p2(x)之间的相似度用巴氏系数(BC)定义为：

(5)

在离散域上BC定义为：

(6)

其中p1(x)和p2(x)密度是已知的评分数据，用户u和v的评分别用Puh和Pvh来评估其离散密度，计算用户u和v之间的BC相似度为：

(7)

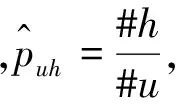
例如：评分在1～5之间，用户u和v的评分向量：ru= (1,0,2,0,1,0,2,0,3,0)T，rv=(0,1,0,2,0,1,0,2,0,3)T，所以用户u和v之间的BC系数为：

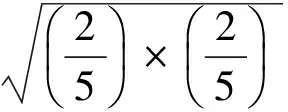
0+0=1

(8)

2.2 巴氏系数相似度

基于巴氏系数提出一种新的相似性度量方法——巴氏系数相似度，利用用户的所有评分来计算两个用户之间的相似度。Jaccard相似性计算的是共同评分项目数所占的比重，利用式(4)描述两个用户评分之间的全局相似性；由于Pearson相似性不能区分数值的差距，而巴氏系数是对相同评分数值重叠的近似计算，可以用来计算评分分布规律相似度，将两者相乘不仅可以发现评分分布规律还能区别评分数值上的差距，互相弥补其缺陷。令用户u和v评价的两个项目分别为Iu和Iv，用户u和v评价的两项目之间的局部相似性定义如下。

(9)

设两个用户的评分向量为：ru=(1,1,3,3,2)，rv=(3,3,5,5,4)。其simpear(u,v)=1，simloc(u,v)=0.16，其实这两个用户评分整体偏差较大，相似度较低，其局部相似性设计更为合理。

当两个用户之间的共同评分数为0即Iu∩Iv=∅，巴氏系数相似度也可以计算用户u和v之间的相似度，其相似度等于局部相似度，且数值往往很小，远远小于1，即sim(u,v)=simloc(u,v)<<1。当两个用户之间存在共同评分数时其整体相似度被分割成全局和局部相似性两部分，且sim(u,v)>simJac(u,v)>simloc(u,v)。如果两个用户在全局角度上是相似的，则BC(u,v)提高用户u和v的评分之间的局部相似性，另一方面，如果用户u和v完全不相似，则BC(u,v)降低两个用户评分之间的局部相似度的重要性。局部相似性提供非常重要的用户局部信息，局部相似性也必须提供用户评分之间的正和负关系。

融合局部相似度和全局相似度得到最终的相似度值。当BC(u,v)=1时局部相似度的作用最大，为相同项目提供最大的局部相似性；当BC(u,v)=0时局部相似度为0，此时全局相似度就是最终的相似度值。

(10)

本文提出的巴氏系数相似度特点在于整合利用巴氏系数、Jaccard和Pearson相关系数互相弥补其缺陷，完美诠释两个用户之间的相似性。考虑了用户评分的全局信息和局部信息，不再仅依靠用户对共同项目的评分，即使没有也可以计算两个用户(项目)之间的相似性，不受数据稀疏性的影响。计算相似性时利用用户对项目的所有评分，多方面的考虑可能影响用户之间相似度的因素，考虑用户评分的全局相似性和局部相似性。

2.3 BCCF算法

在基于近邻协同过滤算法的基础上，利用巴氏系数改进相似度计算，BCCF的算法流程。

算法：BCCF算法

输入：用户——项目的评分矩阵Rm×n，最近邻居数目k。

输出：目标用户u对未知项目的预测评分集。

算法步骤：

步骤1由数据集得到评分矩阵Rm×n。

步骤2用式(4)计算用户u和用户v的全局相似度(当u=v时令simJac(u,v)=0)。

步骤3利用式(7)来得到用户u和用户v分别评价项目的评分分布规律(当u=v时令BC(u,v)=0)。

步骤4利用步骤3的计算结果，并通过式(9)计算用户u和用户v的局部相似度(当u=v时令simloc(u,v)=0)。

步骤5根据步骤3和步骤4得到的全局相似度和局部相似度利用式(10)进行融合，形成最终的相似度。

步骤6利用步骤5计算任意两两用户之间的相似度，最终形成相似度矩阵，然后将目标用户u与其他用户v之间的最终相似度递减排序{sim(u,v1)>sim(u,v2)>…>sim(u,vm)}，选择相似度排序中前k个用户作为目标用户u的最近邻居，k个最近邻居用户构成目标用户u的最近邻居集合Iu={v1,v2,…,vk}。

步骤7已知评分矩阵R和最近邻居集合Iu={v1,v2,…,vk}，由k个最近邻居用户对未知项目i的评分，通过加权平均求和得到目标用户u对该项目的预测评分Pu,i，公式如下：

(11)

算法结束。

3 实验与分析

3.1 实验数据集

为了检验提出方法的有效性，在Movielens_100K和Movielens_1M数据集上分别进行验证，数据集的具体参数如表1所示。

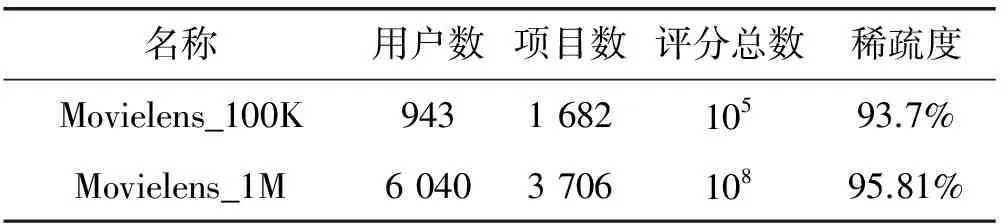
表1 实验数据集的具体参数

本文实验环境为：Windows 7操作系统，内存为4G，Intel(R)Core(TM)i3-4150 CPU3.5 GHz开发工具使用Matlab2013b。

3.2 评价标准

为了反映实际情况的预测误差，本文采用平均绝对误差MAE和均方根误差RMSE从不同侧重点来衡量算法的准确性。设在训练集上得到用户的预测评分集合为p={pu,1,pu,2,…,pu,n}，用户实际评分集合为r={ru,1,ru,2,…,ru,n}，通过计算两集合评分的平均差值或绝对平均差值来衡量推荐的精确率。则平均绝对误差MAE定义为：

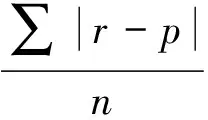
(12)

RMSE同样用来衡量推荐的精确率，RMSE更侧重于预测评分与实际评分差值的绝对值，相对MAE加大了惩罚力度，RMSE值越小，则MAE值越小，预测评分与实际评分越接近，推荐精确度越高。均方根误差RMSE定义为：

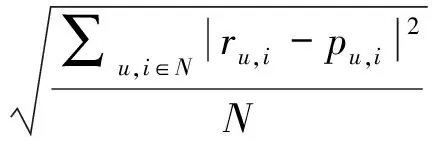
(13)

3.3 实验结果与分析

本实验在Movielens不同大小的数据集上分别进行验证，将Movielens数据集按一定比例(本实验采用8∶2比例)随机分为训练集和测试集，同时进行10次交叉实验求得平均值作为最终结果。

(1) 在Movielens_100K数据集上传统相似度比较

当邻居数目k从5～30变化时，比较Pearson相关系数、Jaccard相似度的MAE值。Jaccard在全局上计算共同评分所占比重，由巴氏系数取得评分分布并结合Pearson相关系数在局部上得到评分之间的相似性，由全部和局部相似性得到巴氏系数相似性；从图1中可以看出：随着用户邻居数目k的增大，本文提出的BCCF算法其MAE值总体趋于减少，当邻居数达到30时MAE值基本稳定；相对于传统的Jaccard和Pearson相关系数计算方法，BCCF算法的MAE值最低且相对稳定。

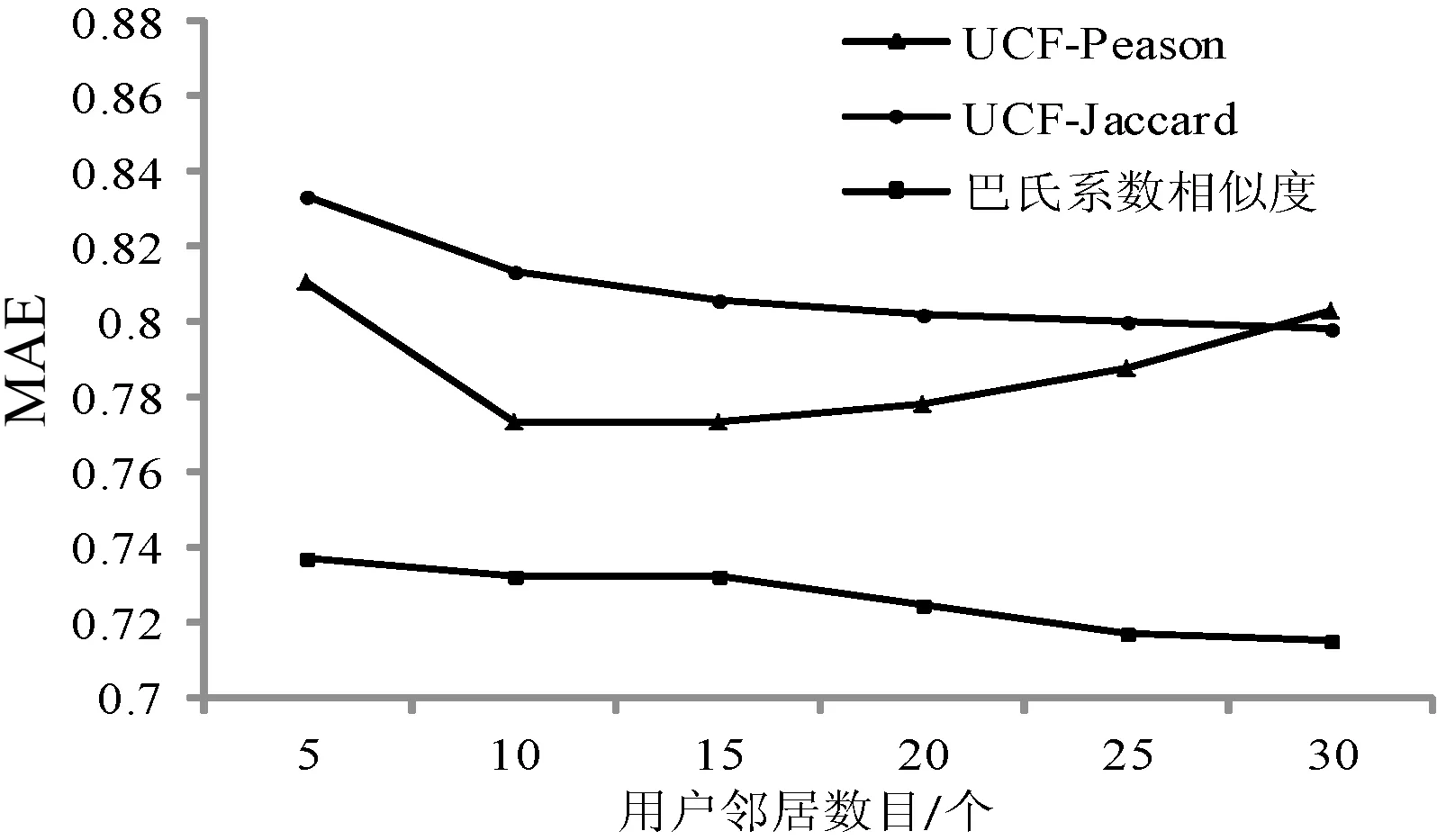
图1 巴氏系数相似度与传统相似度的MAE比较

(2) Movielens_100K数据集上不同算法之间对比

实验中最近邻居数k分别取5、10、15、20、25和30，根据实验(1)中选取巴氏系数相似性作为算法的相似度计算方法，本文提出的BCCF算法分别与文献[7]中提出的改进相似度算法(JPCC)、文献[8]中提出的改进算法 (JMSD) 在Movielens_100K数据集上进行 MAE和RMSE值对比。

由图2和图3可以看出，在Movielens_100K数据集上改进算法BCCF与传统的JPCC算法相比MAE在趋于稳定状态下降低了6%、RMSE降低了2%；比JMSD算法相比MAE在趋于稳定状态下降低了10%、RMSE降低了5%。在Movielens_100K数据集上BCCF算法的精确性比上述所参照的经典论文算法的精确度有所提高，从一个侧面说明了在该数据集中实际存在着用户对项目的共同评分很少的情况下进行优化的方案，即采用巴氏系数进行用户间所有的评分能够进一步提高算法的精度。

图2 Movielens_100K数据集上三种算法的MAE对比

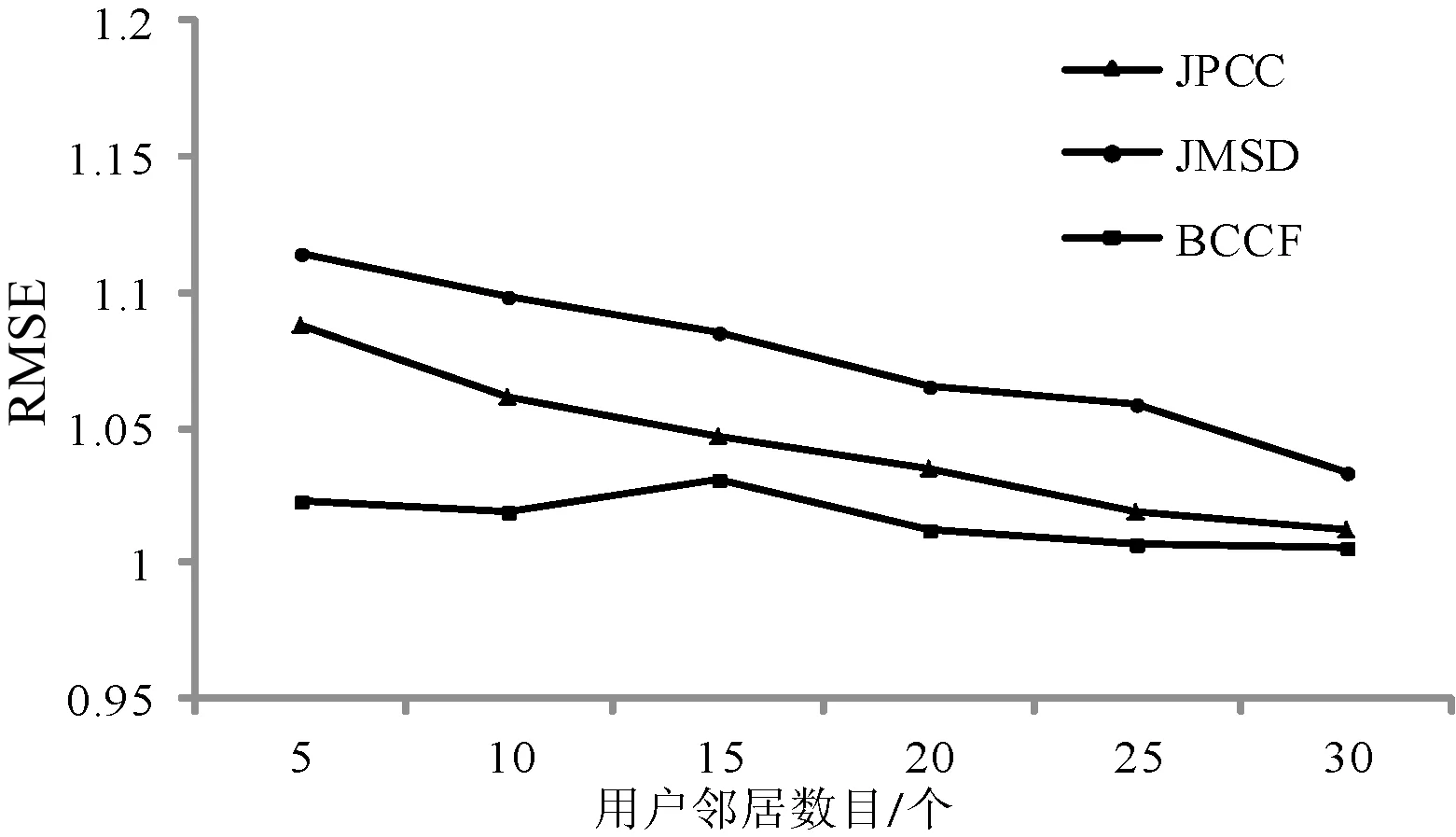
图3 Movielens_100K数据集上三种算法的RMSE对比

(3) 在Movielens_1M数据集上不同算法之间对比

本节实验中最近邻居数k为 5～30，根据实验(1)中选取巴氏系数改进相似性作为算法的相似度计算方法，在Movielens_1M数据集上，本文提出的BCCF算法分别与JPCC算法、JMSD算法进行 MAE和RMSE值对比。其效果分别如图4、图5所示。

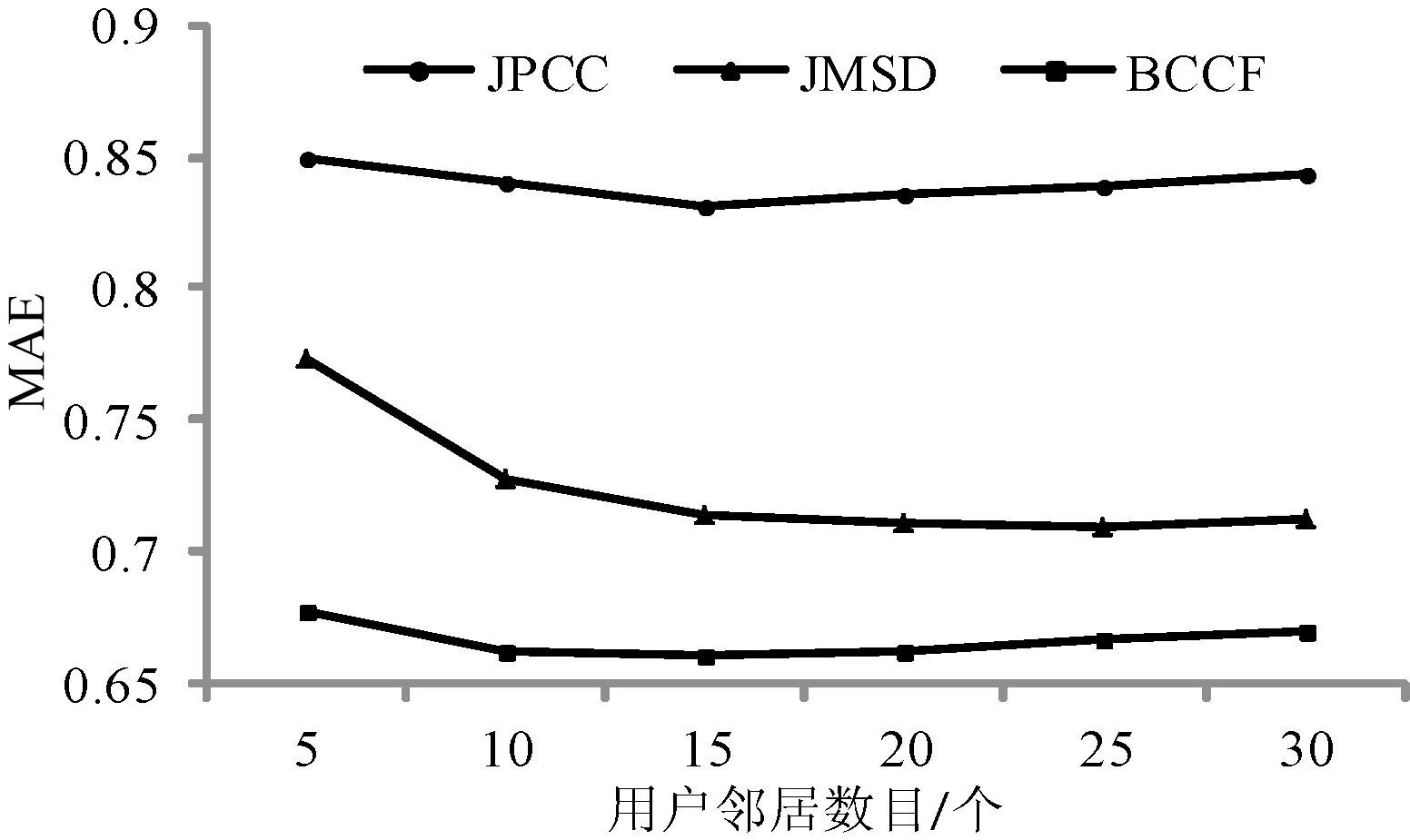
图4 Movielens_1M数据集上三种算法的MAE对比

图5 Movielens_1M数据集上三种算法的RMSE对比

由图4和图5可以看出，在Movielens_1M数据集上改进算法BCCF与传统的JPCC算法相比在趋于稳定状态下MAE降低了20%、RMSE降低了17%，比JMSD算法相比在趋于稳定状态下MAE降低了10%、RMSE降低了4%。RMSE和MAE值越小则表示推荐质量越好，且在Movielens_1M数据集上BCCF算法的RMSE和MAE值比在Movielens_100K数据集上实验结果更小，说明数据集越稀疏其BCCF算法的MAE和RMSE性能越好，说明本文提出的一种巴氏系数改进相似度的协同过滤算法能有效缓解评分数据稀疏性问题及其带来的推荐精度问题。

4 结 语

本文提出了一种基于巴氏系数的改进相似度计算方法，考虑了用户评分的全局和局部相似性，能更全面分析用户之间的相似性，并在此基础上设计了BCCF算法。通过与传统协同过滤算法比较，实验结果表明：BCCF算法不再仅依赖于共同评分，解决了推荐系统中数据极大稀疏时无法计算相似度，以及由数据稀疏性带来的推荐精度问题；现实情况中用户对项目的共同评分很少甚至没有，故BCCF有很强的实用性，BCCF更适用于评分矩阵稀疏的数据集；BCCF合理利用用户的每一个评分，根据用户的评分来发现其内在的相关性。考虑用户的所有评分，造成计算相似度时其时间复杂度增加，对巴氏系数相似度计算进行优化，找到能降低其时间复杂度方法，进一步提高算法性能。

[1] Bobadilla J,Ortega F,Hernando A,et al.Recommender systems survey[J].Knowledge-Based Systems,2013,46(1):109-132.

[2] Lien D T,Phuong N D.Collaborative filtering with a graph-based similarity measure[C]//Computing,Management and Telecommunications (ComManTel),2014 International Conference on.IEEE,Da Nang,2014:251-256.

[3] Han X,Wang L,Farahbakhsh R,et al.CSD:A multi-user similarity metric for community recommendation in online social network[J].Expert Systems with Applications,2016,53:14-26.

[4] 荣辉桂,火生旭,胡春华.基于用户相似度的协同过滤推荐算法[J].通信学报,2014,35(2):16-24.

[5] 吴毅涛,张兴明,王兴茂.基于用户模糊相似度的协同过滤算法[J].通信学报,2016,37(1):198-206.

[6] 孙达明,张斌,张书波,等.一种流行性与相似性结合查询推荐策略[J].小型微型计算机系统,2016,37(6):1121-1125.

[7] 郑翠翠,李林.协同过滤算法中的相似性度量方法研[J].计算机工程与应用,2014,50(8):147-149.

[8] Bobadilla J,Ortega F,Hernando A,et al.A similarity metric designed to speed up,using hardware,the recommender systems k-nearest neighbors algorithm[J].Knowledge-Based Systems,2013,51(1):27-34.

[9] Pirasteh P,Hwang D,Jung J E.Weighted similarity schemes for high scalability in user-based collaborative filtering[J].Mobile Networks & Applications,2015,20(4):497-507.

[10] Sun H F,Chen J L,Yu G,et al.JacUOD:A new similarity measurement for collaborative filtering[J].Journal of Computer Science & Technology,2012,27(6):1252-1260.

COLLABORATIVEFILTERINGALGORITHMBASEDONIMPROVEDSIMILARITYMEASUREWITHBHATTACHARYYACOEFFICIENT

Wu Wenqi Wang Jianfang Zhang Pengfei Liu Yongli
(SchoolofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)

Aiming at the problem of low-quality recommendation and data sparsity, we proposed a collaborative filtering algorithm based on improved similarity measure with Bhattacharyya coefficient. First, we use Jaccard similarity to calculate the global similarity between users based on neighbor cooperative filtering algorithm. Secondly, we use the Bhattacharyya coefficient to obtain the whole law of the grade distribution. And we combine the Pearson correlation coefficient to calculate the local similarity. Finally, we fuse the global similarity and local similarity to obtain final similarity metric. The experimental results show that algorithm can get better recommendation results on sparse data sets. It effectively mitigates the sparseness of scoring data and improves the recommended accuracy.

Collaborative filtering Data sparsity Bhattacharyya coefficient Similarity measure

2016-08-31。国家自然科学基金项目(61202286)；河南省高等学校青年骨干教师资助计划项目(2015GGJS-068)。武文琪，硕士生，主研领域：数据挖掘，推荐算法。王建芳，副教授。张朋飞，硕士生。刘永利，副教授。

TP391

A

10.3969/j.issn.1000-386x.2017.08.047