Gauss诱导核模糊c均值聚类算法

文传军 詹永照

1(常州工学院数理与化工学院 江苏 常州 213002) 2(江苏大学计算机科学与通信工程学院 江苏 镇江 212013)



Gauss诱导核模糊c均值聚类算法

文传军1詹永照2

1(常州工学院数理与化工学院 江苏 常州 213002)2(江苏大学计算机科学与通信工程学院 江苏 镇江 212013)

针对核模糊聚类算法优异的非线性表达能力，提出一种Gauss诱导核模糊c均值聚类算法(GIKFCMs)。首先，基于核目标函数和梯度法，得到特征空间聚类中心表达式，并通过内积运算得到聚类中心与样本的核矩阵表达式。其次，取核目标函数中的核函数为Gauss核函数，并利用梯度法得到输入空间聚类中心表达式。最后将聚类中心与样本的核矩阵代入输入空间聚类中心表达式中，从而得到GIKFCMs核聚类中心计算方法，同时得到相应的GIKFCMs核聚类算法。研究GIKFCMs算法的相关性质，分析算法的收敛性和初始化约束。GIKFCMs算法克服了原有核聚类算法在收敛性与初始化约束方面的缺陷。通过仿真实验验证了该算法的有效性。

核方法 模糊聚类 非线性映射 核聚类中心 算法等价性证明

0 引 言

自核方法被成功地应用于分类器支持向量机(SVM)[1]以来，即受到机器学习和模式分类领域研究者的广泛关注和研究，并进一步将其推广应用到特征提取[2]、模糊聚类[3]等领域。

核方法将输入空间的非线性关系通过非线性映射转换为高维特征空间的线性关系，增大了模式间的差异性刻画。且利用核函数表示高维特征空间中的内积运算，无需明确知道具体的非线性映射形式，克服了机器学习的维数灾难问题，所以在模糊聚类领域有着广泛而成功的应用。

由于核方法利用核函数表达特征空间中的内积运算，且特征空间中的空间距离可转换为内积运算形式。所以核方法适合于在特征空间中仅存在内积和距离运算的算法。聚类中心是模糊聚类算法[4]的重要组成部分，由于核方法中非线性映射的无具体形式给出，因此在模糊聚类算法中应用核方法时，一个关键性的问题是如何表示核聚类中心。

自文献[5-6]提出硬核聚类算法以来，将核方法应用于聚类算法的各种核模糊聚类算法应运而生[7-9]。通过对比研究可以发现，这些核模糊聚类算法的根本原理都是相同的，即在各种模糊聚类算法中结合应用核方法。这些核模糊聚类算法的聚类目标函数和模糊隶属度公式在形式上是一致的，不同之处在于核聚类中心的推导原理及表现形式的不同。

本文在上述研究工作的基础上，以核聚类中心推导原理为分类标准，归纳总结了现有的三种基本核模糊聚类算法。在此基础上推导得到一种新的核聚类中心计算方法，称所对应的核聚类算法为Guass诱导核模糊c均值聚类算法(GIKFCMs)。GIKFCMs首先基于高斯核函数和核聚类目标函数，并利用梯度法分别得到特征空间和输入空间的聚类中心表示式。然后借助核方法和内积运算得到样本与特征空间聚类中心的核矩阵。最后通过该核矩阵将特征空间和输入空间的聚类中心表示式结合起来，从而得到了GIKFCMs算法的核聚类中心计算方法。GIKFCMs算法的核聚类中心与一般核模糊聚类目标函数及核模糊隶属度组成了GIKFCMs核模糊聚类算法。所提出的GIKFCMs算法克服了原有聚类算法在收敛性和初始化方面的缺陷，仿真实验验证了所提出算法的有效性。

对于已知的三种核模糊聚类算法，它们的推导原理和算法实现机制是不同的，但目前没有文献研究对它们的原理和实现进行归纳比较分析。

1 模糊c均值聚类算法及核模糊c均值聚类算法

模糊c均值聚类算法(FCM)是一种典型的并成功应用的模糊聚类算法。众多模糊或核模糊聚类算法都是在其基础之上改进得到的，基于FCM算法可直观简洁地阐述核模糊聚类算法的原理和性质，核模糊c均值聚类算法(KFCM)相应结论可平行推广到其他核模糊聚类算法。

1.1 模糊c均值聚类(FCM)

设X={x1,x2,…,xn}为样本空间Rd中的一个有限数据集，xj为该样本空间中的一个样本向量。 FCM采用模糊划分的方法，用值在0到1之间的隶属度确定每个样本属于各组聚簇的程度，并将数据集X划分为c个模糊聚簇。FCM最优化准则即为最小化目标函数，可表示为：

(1)

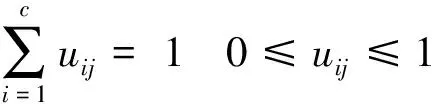
(2)

其中V=[vi]c×d为聚类中心矩阵，dij=‖xj-vi‖表示xj与vi在样本输入空间中的距离，一般采用欧氏距离(Euclid)表示。U=[uij]c×n表示模糊隶属度矩阵，uij(0≤uij≤1)表示样本xj属于第i组聚簇的隶属程度；m(m>1)称为模糊指标。通过梯度法得到FCM模糊隶属度及聚类中心迭代公式，如式(3)、式(4)所示：

(3)

∀i=1,…,c∀j=1,…,n

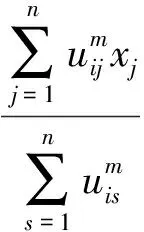
(4)

∀i=1,…,c

由于FCM算法在输入空间中采用欧氏距离，所以仅可对在输入空间中具有超球体结构的可分数据集作有效聚类，而对蕴含非线性可分关系的数据集不能作有效聚类[7]。

1.2 核方法(NM)

对于X={x1,x2,…,xn}，xj∈Rd，函数K:X×X→R在满足对称正定的条件下称为Mercer核函数，任一核函数总可以表示为：

K(xi,xj)=Φ(xi)·Φ(xj)

(5)

其中Φ为从低维输入空间X到高维特征空间F的非线性映射，即有：

Φ:X→F

(6)

非线性映射Φ的形式并不需要明确给出，数据集X通过Φ映射到空间F，可表示为Φ(X)={Φ(x1),Φ(x2),…,Φ(xn)}，由式(5)知可利用核函数表示高维特征空间中向量间的欧氏距离。

‖Φ(xi)-Φ(xj)‖2=

(Φ(xi)-Φ(xj))·(Φ(xi)-Φ(xj))=

Φ(xi)·Φ(xi)+Φ(xj)·Φ(xj)-2Φ(xi)·Φ(xj)=

K(xi,xi)+K(xj,xj)-2K(xi,xj)

(7)

利用核函数表示高维特征空间中向量间距离关系，即称之为核方法。核方法适合于在高维特征空间中仅存在点积运算和距离关系的算法。

常用的核函数包括：

(1) 多项式核函数：KP(xi,xj)=(xi·xj+b)d，b>0，d∈N。当b=0，d=1时，得到线性核函数，即有KL(xi,xj)=xi·xj。

(2) Sigmoid核函数：KS(xi,xj)=tanh(α(xi·xj)+β)，α,β>0。

1.3 核模糊c均值聚类算法(KFCM)

核模糊c均值聚类算法(KFCM)即是将核方法应用于模糊c均值聚类算法。模糊聚类算法主要由目标函数、模糊隶属度和聚类中心三部分构成，由式(1)、式(3)可知，目标函数和模糊隶属度仅含有距离运算，满足应用核方法的要求。由式(4)可知，聚类中心并不满足应用核方法的条件，因此不能直接使用核方法处理聚类中心。目前主要有三种不同的聚类中心表现方法，将在第2节中进行介绍，这里主要给出核方法在聚类目标函数和模糊隶属度中的应用。

由式(1)、式(7)可知，KFCM算法目标函数可表达为：

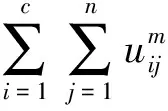
(8)

其中dKij=‖Φ(xj)-Φ(vi)‖表示特征空间中向量Φ(xj)与聚类中心Φ(vi)的欧氏距离，且可利用核函数表达出来。即有：

(9)

由式(3)、式(7)可知，KFCM算法模糊隶属度可表达为：

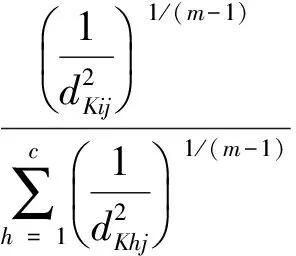
(10)

∀i=1,…,c∀j=1,…,n

对比式(1)、式(8)、式(3)和式(10)可知，FCM与KFCM算法的目标函数和模糊隶属度表达形式基本一致。

2 核聚类算法分类

核聚类中心的表示是FCM算法与核方法结合生成KFCM算法的关键，现有研究文献主要包含了三种不同的核聚类中心表现方法。本文根据其推理原理的不同分别做了这三种核聚类中心的命名和分类。由于这些核聚类算法的目标函数和模糊隶属度是相同的，所以以核聚类中心命名相应的核模糊聚类算法，并在2.1至2.3节中进行了阐述。

2.1 隐核模糊c均值聚类算法(HKFCMs)

文献[7]在硬核聚类算法的基础上提出了一种核模糊聚类算法。在这种核聚类算法中，核聚类中心Φ(vi)利用梯度法以隐式形式表现在核矩阵中，因此将该算法核聚类中心命名为隐核聚类中心，相应的核聚类算法为隐核模糊c均值聚类算法(HKFCMs)。

令式(8)对特征空间聚类中心Φ(vi)求偏导，并令求导结果等于0，则有：

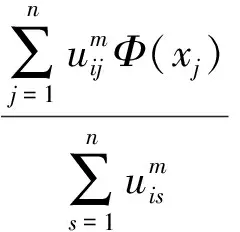
(11)

由于非线性映射Φ具体形式不可知，所以不能显式计算Φ(vi)，将Φ(vi)与Φ(vi)、Φ(xh)分别作内积运算并利用核函数表示出来，得到：

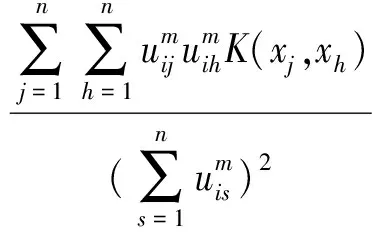
(12)

(13)

类似FCM算法参数迭代估计流程，利用式(8)、式(10)与式(12)、式(13)及AO交替迭代算法，可对数据集X给出模糊聚类划分。在式(12)、式(13)中，特征空间聚类中心Φ(vi)并没有显式给出，但特征空间聚类中心信息已蕴藏在K(vi,vi)及K(xh,vi)中。在最小化目标函数的过程中，HKFCMs算法利用了核聚类目标函数对Φ(vi)的梯度信息，且该算法由式(8)、式(10)、式(12)及式(13)确定。HKFCMs算法没有聚类中心的显示计算公式，所以在算法迭代时只能对模糊隶属度做初始化，从而由式(10)、式(12)及式(13)生成交替迭代序列。

2.2 Gauss核模糊c均值聚类算法(GKFCMs)

文献[8]利用Gauss核函数提出了一种模糊聚类算法，其聚类中心依赖于Gauss核函数计算得到，所以称其为Gauss核聚类中心，称相应的核聚类算法为Gauss核模糊c均值聚类算法(GKFCMs)。

根据Gauss核函数的定义，可以得到式(14)：

(14)

其中KG表示高斯核函数。

对于KFCM目标函数式(8)，取核函数为高斯核函数，由式(8)及式(14)可得到：

(15)

令式(10)中核函数K取为高斯核函数KG,可得到：

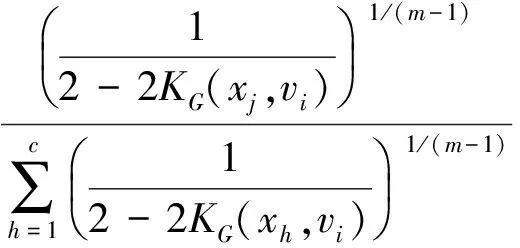
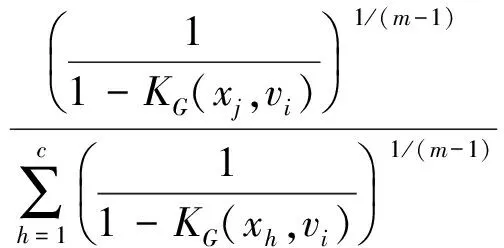
(16)

令式(15)对输入空间聚类中心vi求偏导，并令求导结果等于0，则有：

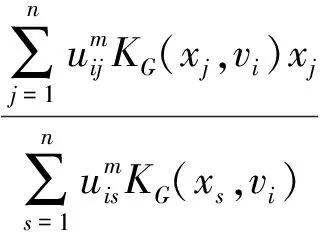
(17)

GKFCMs算法由式(15)-式(17)构成。GKFCMs算法给出了核聚类算法在输入空间中原始聚类中心vi的显式表达。在最小化目标函数的过程中，GKFCMs算法利用了核聚类目标函数对vi的梯度信息。由于GKFCMs算法聚类中心式(17)的右端含有聚类中心vi本身，所以该聚类算法不满足一般聚类算法收敛性证明的基本条件，即要求聚类中心仅为模糊隶属度的函数。因为GKFCMs算法聚类中心式(17)右端既有vi且有uij，初始化uij无法计算聚类中心vi，所以在算法迭代时只能对聚类中心vi作初始化。

2.3 PSO核模糊c均值聚类算法(PSO-KFCMs)

生物进化算法越来越多的被引入到模糊聚类算法中，用于模型的参数估计和目标函数求解。此类算法的优势在于全局优解搜索性能和不依赖于梯度信息，适合于非线性、不可微和多峰值复杂问题的优化。由于粒子群(PSO)算法是基于实数域编码并在输入解空间全局搜索优解的，适合于对模糊聚类算法聚类中心估计寻优。文献[10-11]利用PSO算法对聚类中心进行编码寻优求解，文献[9]进一步将其与核方法结合起来，称这样的聚类中心为PSO核聚类中心，相应的核聚类算法为PSO核模糊c均值聚类算法(PSO-KFCMs)。基本PSO在每次迭代中粒子根据自身pbest和全局gbest来修正自身飞行速度。

粒子的速度及位置更新公式分别为：

vij(t+1)=wvij(t)+c1r1[pij(t)-xij(t)]+

c2r2[gij(t)-xij(t)]

(18)

xij(t+1)=xij(t)+vij(t+1)

(19)

其中c1、c2为加速因子，取为正的常数；r1、r2为[0,1]之间的随机数，w称为惯性因子。

模糊聚类算法一般定义式(20)为PSO适应度函数。

(20)

PSO-KFCMs算法在输入空间中对聚类中心vi寻优，没有利用核目标函数对于Φ(vi)或vi的梯度信息，而仅是在适应度函数的指引下修正迭代寻优路径和速度。PSO-KFCMs算法利用PSO算法对聚类中心寻优，其模糊隶属度和目标函数由式(8)和式(10)确定。PSO-KFCMs算法没有聚类中心的计算公式，其聚类中心取值依赖于PSO算法在解空间中的搜索，所以在算法迭代时只能对聚类中心做初始化。

3 Gauss诱导核模糊聚类算法(GIKFCMs)

3.1 Gauss诱导核模糊聚类算法

GKFCMs算法由于其聚类中心公式的右端含有聚类中心本身，所以不满足聚类算法收敛性条件，且HKFCMs算法和GKFCMs算法在迭代初始化上存在缺陷。在2.1节隐核聚类中心和2.2节Gauss核聚类中心的基础上，推导出了一种新的核聚类中心计算方法，并称所得到的聚类中心为Gauss诱导核聚类中心，相应的核聚类算法为Gauss诱导核模糊c均值聚类算法(GIKFCMs)。

类似HKFCMs算法，令核目标函数式(8)对特征空间聚类中心Φ(vi)求偏导，并令求导结果等于0，则有：

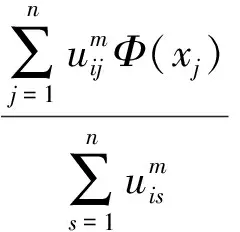
(21)

对式(21)两边乘以Φ(xj)，得到：

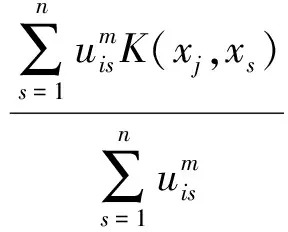
(22)

令式(22)中核函数取为Gauss核函数，得到：

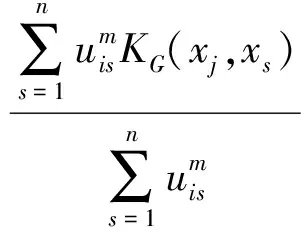
(23)

类似GKFCMs算法，令核目标函数式(8)中的核函数为Gauss核函数，得到：

(24)

令式(24)对输入空间聚类中心vi求偏导，并令求导结果等于0，则有：

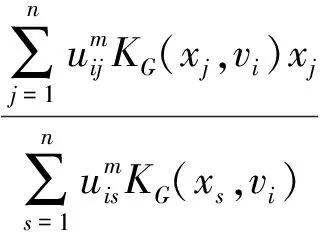
(25)

再将式(23)代入式(25)右端，即有：

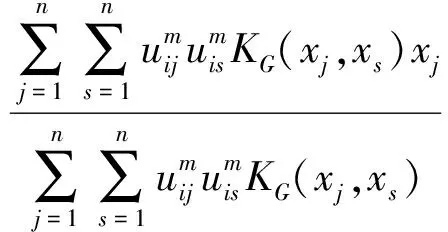
(26)

根据GIKFCMs算法聚类中心推导过程可知，该聚类中心既利用了隐核聚类中心对Φ(vi)的梯度信息，又使用了GKFCMs聚类中心对vi的梯度信息，且聚类中心vi在输入空间显式表示，所以是一种新的核聚类中心确定方法。特别强调的是，如式(26)所示，GIKFCMs聚类中心vi的显式表达式右端并不包含聚类中心vi，这是与GKFCMs算法聚类中心式(17)所截然不同的，从而使得GIKFCMs算法满足聚类算法收敛性证明的要求。同时也使得GIKFCMs算法可类似FCM算法，不仅可以对聚类中心作初始化，而且可以对模糊隶属度作初始化。

很显然，GIKFCMs算法的目标函数和模糊隶属度与GKFCMs算法相同，所以该算法由式(16)、式(24)和式(26)构成。

3.2 Gauss诱导核模糊聚类算法迭代流程

GIKFCMs用下列步骤确定聚类中心vi和隶属矩阵U=(uij)c×n：

步骤2用式(26)计算c个聚类中心vi，i=1,…,c。

步骤3根据式(24)计算代价函数。如果它小于某个确定的阈值，或它相对上次价值函数值的改变量小于某个阈值，则算法停止。

步骤4用式(16)计算新的U矩阵。返回步骤2。

上述迭代算法也可以先初始化聚类中心，然后再执行迭代过程。

为了避免分母为0不可运算，若某样本xj与某聚类中心vi重合，则规定该样本归于该类的隶属度为1，归于其他类的隶属度为0即可。

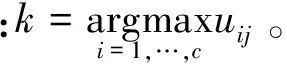
4 各核模糊聚类算法性质分析

4.1 各核聚类算法聚类中心确定方法的性质

四种推导原理不同的核聚类中心计算方法，引出了四种不同的核模糊聚类算法。这些核模糊聚类算法的目标函数和模糊隶属度表现形式是一致的。

HKFCMs算法将核目标函数JKFCM(U,V)对特征空间聚类中心Φ(vi)求偏导计算极值点，得到Φ(vi)的显式表达式，但由于非线性变换Φ的映射形式不可知，使得算法不能直接利用Φ(vi)的显式信息。因此，将Φ(vi)与Φ(vi)及Φ(xj)作点积运算，并利用核函数得到Φ(vi)的隐示表达式。隐核聚类中心聚类算法利用的是目标函数关于Φ(vi)对梯度信息进行参数优化估计，该算法的核函数具有一般性，能够选择任意核函数。

GKFCMs算法令核函数为Gauss核函数，利用Gauss核函数中蕴藏‖x-y‖2的特殊性，将核目标函数对输入空间聚类中心vi求导，得到vi的显示表达式。因此GKFCMs算法聚类中心方法只能选取Gauss核函数。在Gauss核聚类中心公式的右端，还包含了聚类中心vi本身，不满足聚类算法收敛性证明的条件，因此不能仿照FCM算法证明其算法收敛性[4]。

PSO-KFCMs算法聚类中心确定方法与PSO-FCMs聚类中心确定原理和计算流程相同，即利用PSO生物进化算法在输入空间中依适应度函数值迭代寻优聚类中心。该算法和HKFCMs算法一样，可以选择任意核函数。

GIKFCMs算法首先利用Gauss核函数及隐核聚类中心式(11)，得到式(23)的结论，然后将其与Gauss核聚类中心表达式(25)相结合，得到Gauss核诱导聚类中心式(26)。在Gauss核诱导聚类中心的推导过程中，既利用了隐核聚类中心关于Φ(vi)对梯度信息，又结合了Gauss核聚类中心关于vi对梯度信息，且在输入空间中显式表达vi，所以是一种与前述三种方法所不同的核聚类中心计算方法。很显然，GIKFCMs算法和GKFCMs算法一样，也只能选取Gauss核函数，但GIKFCMs算法聚类中心公式右端不包含聚类中心vi，仅为模糊隶属度uij的函数，这与GKFCMs算法聚类中心截然不同，从而满足了一般模糊聚类算法收敛性证明的要求，进而保证了算法的收敛性[4]。

另外HKFCMs算法和PSO-KFCMs算法的目标函数和模糊隶属度公式是一致的，即采用一般核函数所定义距离生成的目标函数和模糊隶属度。而GKFCMs算法与GIKFCMs算法的目标函数及模糊隶属度公式是相同的，即取核函数为Gauss核函数的特殊情况。

4.2 各核聚类算法的收敛性分析

传统FCM算法是利用梯度算法推导出来的，文献[4]给出了FCM算法收敛性的严谨证明，FCM算法及其改进算法均可以类似得到聚类算法的收敛性。因此可直接根据文献[4]所提供方法证明隐核及Gauss核诱导聚类中心聚类算法的收敛性，这两种核模糊聚类算法所产生的迭代序列将收敛于核目标函数的极小值点或鞍点。对于PSO核模糊聚类中心聚类算法而言，由于核模糊聚类目标函数转换为PSO算法的适应度函数，所以聚类算法的收敛性由PSO算法的收敛性决定。

对于GKFCMs算法，并不能够运用文献[4]的方法判定聚类算法的迭代收敛性，因为文献[4]收敛性证明方法要求聚类中心仅为模糊隶属度的函数。而GKFCMs算法聚类中心公式右端包含聚类中心本身，并不满足聚类算法迭代收敛条件，其算法收敛性的理论证明需要作进一步研究。

4.3 各核聚类算法迭代初始化的要求

GKFCMs算法由式(15)-式(17)确定，其聚类中心式(17)右端含有聚类中心vi，因此不能利用模糊隶属度的初始化计算GKFCMs算法聚类中心。所以GKFCMs算法只能先对聚类中心进行初始化，否则无法进行算法的迭代计算。HKFCMs算法由式(12)、式(13)、式(15)和(16)确定，对于HKFCMs算法而言，由于其在核映射空间中以核矩阵形式隐式表达聚类中心，没有显示的聚类中心表示和计算公式，所以HKFCMs算法只能对模糊隶属度作初始化。而GIKFCMs算法由式(16)、式(24)和式(26)确定，其迭代方式和FCM算法类似，既可以对聚类中心进行初始化，也可以对模糊隶属度进行初始化，反映了该算法的迭代通用性。对于PSO-KFCMs算法而言，它在输入空间中利用PSO算法搜索聚类中心优解，不能利用模糊隶属度求解聚类中心。因此该算法仅能对聚类中心作初始化并根据适应函数取值进行迭代更新。

5 仿真实验

为了验证本文所提出的GIKFCMs 算法的有效性，将GIKFCMs算法与在第2节中所归纳的核聚类算法做对比测试。在第2节中，GIKFCMs算法和HKFCMs 、GKFCMs算法的推导原理相似，都是利用梯度法得到聚类算法参数计算公式，并通过AO交替迭代流程进行参数估计。这三种算法进行对比测试具有可比性，因此选用HKFCMs 、GKFCMs算法与GIKFCMs算法做对比测试。

5.1 公共测试数据集

基于UCI机器学习数据库中的公共数据集进行算法比对测试，所选数据集为Iris数据集，数据集的信息如表1所示。

表1 iris实验数据集

5.2 仿真实验说明

在测试时，三种核聚类算法都选用Gauss核函数，Gauss核函数需要对Gauss核参数σ赋值，取核参数σ取值范围为[21,22,23,24]，聚类算法模糊指标m取值为[2,3,4]。在取核函数为Gauss核函数的情况下，HKFCMs算法由式(13)、式(15)、式(16)作聚类运算，GKFCMs算法由式(15)-式(17)作聚类运算，而GIKFCMs算法由式(16)、式(24)、式(26)作聚类运算。每种聚类算法根据参数和数据集进行10次测试，计算各类聚类平均精度。很显然这三种核聚类算法的核模糊隶属度及聚类目标函数是相同的，区别在于聚类中心的表达上，其中GKFCMs和GIKFCMs算法在输入空间中寻找聚类中心，而HKFCMs算法在核映射空间中隐式表现了聚类中心。在算法迭代的初始化方面，如4.3节分析所述，GKFCMs、GIKFCMs算法选择对聚类中心做初始化，HKFCMs算法选择对模糊隶属度做初始化。

5.3 实验结果及分析

由于三种核聚类算法中存在参数σ和m的设置，且这两个参数的取值对聚类结果有着重要的影响，所以依参数不同取值表现算法聚类结果，三模型聚类结果分别如表2-表4所示。

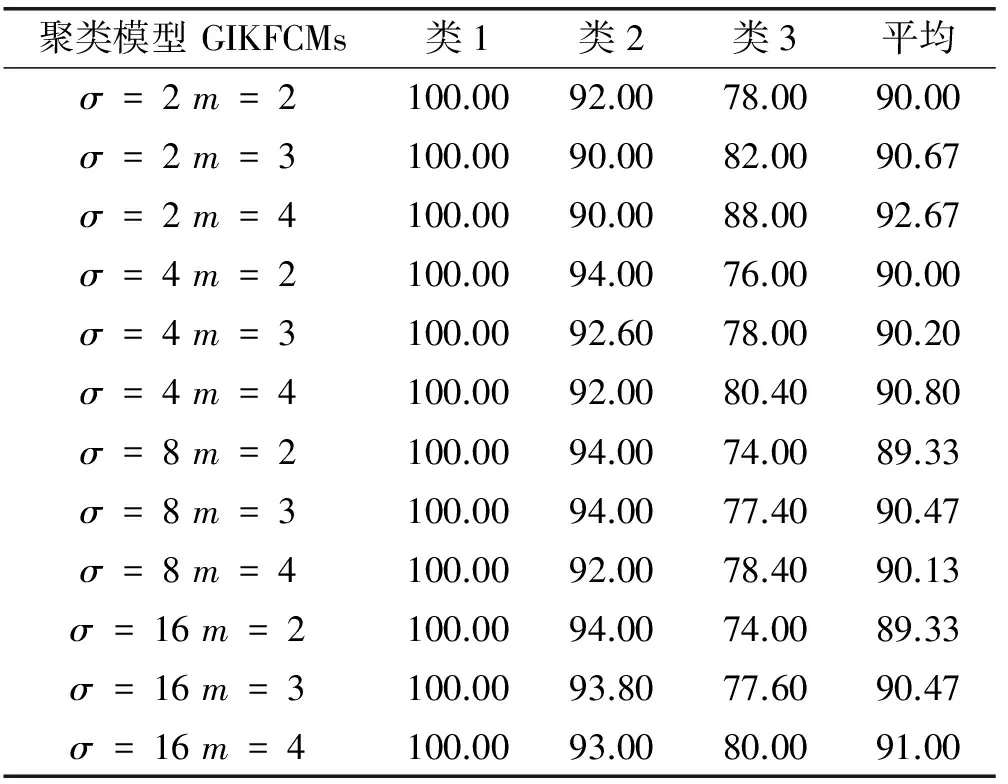
表2 GIKFCMs算法基于Iris数据集的分类精度 %

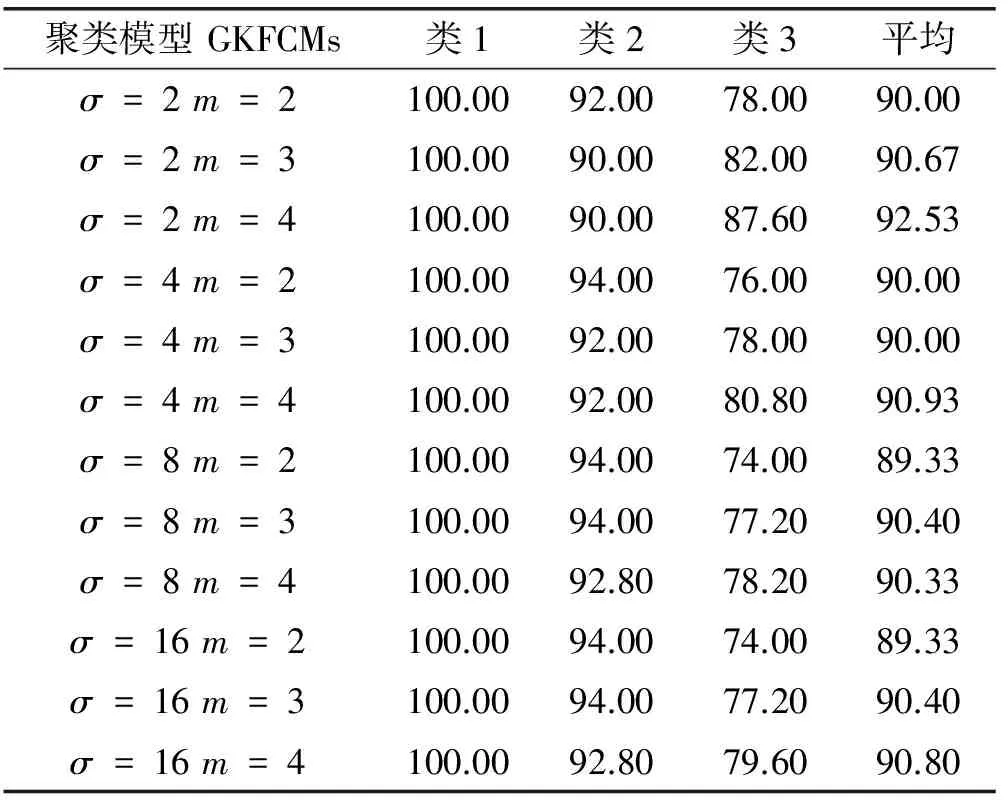
表3 GKFCMs算法基于Iris数据集的测试结果 %

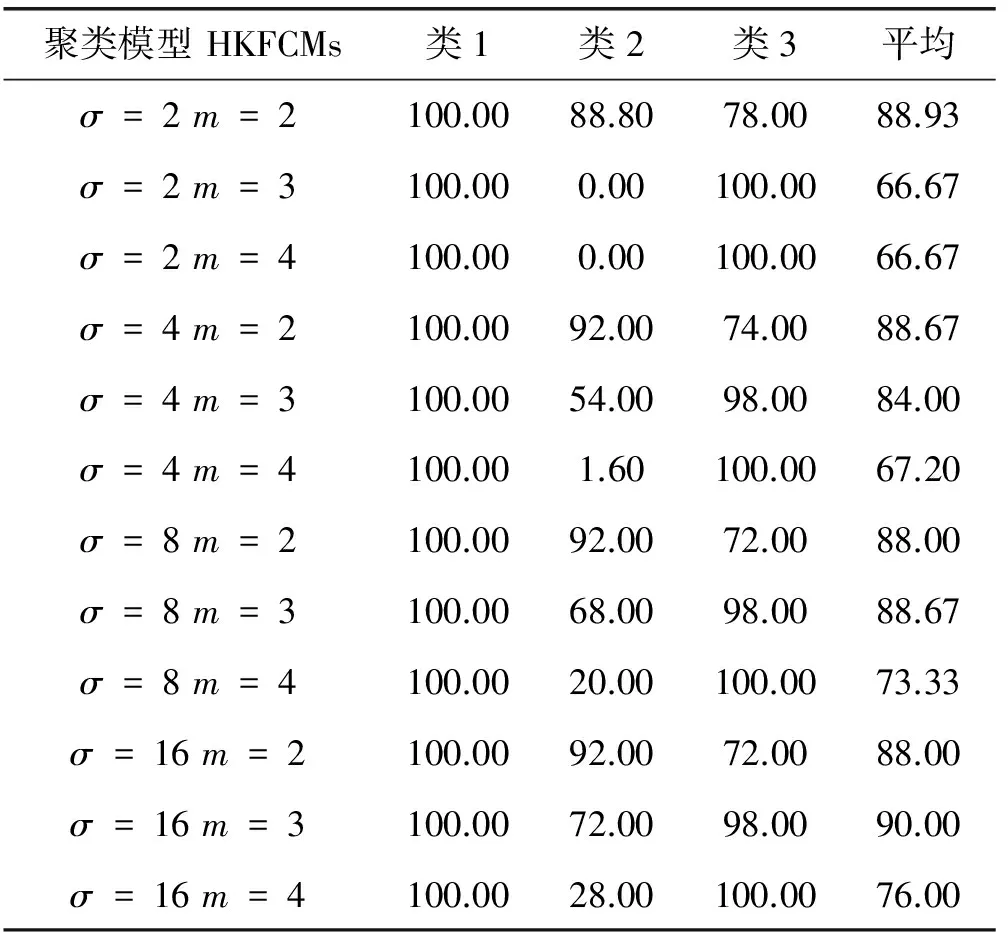
表4 HKFCMs算法基于Iris数据集的分类精度 %

GIKFCMs算法基于数据集iris的最高平均分类精度为92.67%，在参数σ=2，m=4时取得；最低平均分类精度为89.33%，分别在参数σ=8，m=2和σ=16，m=2。在聚类平均精度的基础上，再取聚类平均精度的平均为90.422 5%。

GKFCMs算法基于数据集iris的最高平均分类精度为92.53%，在参数σ=2，m=4时取得；最低平均分类精度为89.33%，分别在参数σ=8，m=2和σ=16，m=2。在聚类平均精度的基础上，再取聚类平均精度的平均为90.39%。

HKFCMs算法基于数据集iris的最高平均分类精度为90.00%，在参数σ=16，m=3时取得，最低平均分类精度为66.67%，分别在参数σ=2，m=3和σ=2，m=4。在聚类平均精度的基础上，再取聚类平均精度的平均为80.51%。

由表2和表3可知，GIKFCMs和GKFCMs算法对于iris数据集都能取得较好的聚类结果，在不同的参数取值情况下，GIKFCMs和GKFCMs算法聚类结果之间各有高低。如当σ=2，m=4时，GIKFCMs平均聚类精度92.67%高于GKFCMs平均聚类精度92.53%；而在σ=4，m=4时，GIKFCMs平均聚类精度90.80%低于GKFCMs平均聚类精度90.93%。但在最高平均分类精度上和聚类平均精度的平均上，GIKFCMs算法是高于GKFCMs算法的，体现了GIKFCMs算法的有效性。由表4可知，HKFCMs算法基于数据集iris的测试结果并不理想，体现在该算法对模糊指标m异常敏感，随着参数m的变化，HKFCMs算法聚类结果波动较大，且聚类结果表现不好。

6 线性KFCM与FCM算法等价性证明的修正

6.1 原等价性证明存在的问题

文献[7]提出命题：对于核模糊c均值聚类算法，若取核函数为线性核函数，即KL(xi,xj)=xi·xj时，KFCM算法等价于FCM算法。虽然这个命题并没有错误，但文中在证明聚类中心等价性时存在错误，因此其证明过程并不能严谨推导出KFCM算法与FCM算法等价的结论。

文献[7]利用线性核函数，得到了：

Φ(xj)·Φ(vi)=K(xj,vi)=xj·vi

(27)

文献[7]由式(27)认为特征空间聚类中心Φ(vi)与输入空间聚类中心vi等价，由核函数性质可知[12]，核函数对应特征空间和特征映射Φ并不唯一，所以由式(27)并不能证明Φ(vi)与vi等价，即不能证明Φ(vi)=vi。

一个简单的反例，设xj=(xj1,xj2,…,xjd)T，取Φ1(xj)=(xj1,xj2,…,xjd,0)T，Φ2(xj)=(0,xj1,xj2,…xjd)T，Φ3(xj)=(xj1,0,xj2,…,xjd)T，很显然特征映射Φ1、Φ2及Φ3皆满足式(27)式约束，但并不能证明Φ1(vi)=Φ2(vi)=Φ3(vi)=vi。

6.2 FCM与线性KFCM算法等价的证明

由于文献[7]所提出的核聚类算法是隐核聚类中心聚类算法，特征空间聚类中心Φ(vi)隐式给出，直接证明Φ(vi)与vi的等价性是非常困难的。因此在证明FCM及KFCM算法等价性时应回避Φ(vi)与vi等价性讨论。

类似隐核聚类中心展开FCM算法，由式(1)、式(3)、式(4)得到式(28)-式(31)：

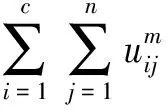
(28)

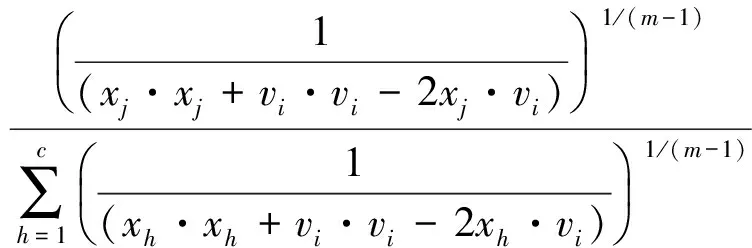
(29)

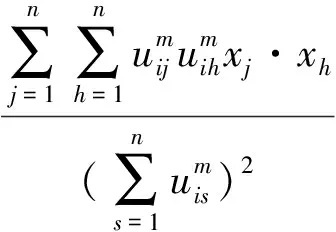
(30)

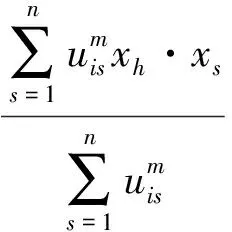
(31)

即可用式(27)-式(31)表示FCM算法，在此种表示中聚类中心vi被隐藏起来。当KFCM算法取为线性核函数式(27)时，KFCM算法表示式(8)、式(10)、式(12)及式(13)转换为FCM算法式(28)-式(31)，从而证明了在线性核函数条件下，FCM算法与KFCM算法是等价的。

7 结 语

核方法具有良好的非线性区分性能，并在机器学习领域应用广泛。模糊聚类算法[13-14]在运用核方法时，核聚类中心的有效表示是运用核方法的关键。所提出的GIKFCMs核模糊聚类算法首先基于Gauss核目标函数和梯度法，分别得到输入空间和特征空间聚类中心表示式。然后借助核方法和内积运算得到样本与特征空间聚类中心的核矩阵。最后应用该核矩阵将特征空间和输入空间的聚类中心表示式结合起来，从而得到了GIKFCMs算法的核聚类中心计算方法及相应的GIKFCMs算法。GIKFCMs算法和HKFCMs、GKFCMs算法相比，不仅能对聚类中心初始化，也能对模糊隶属度作初始化，且满足聚类算法收敛性条件，仿真实验验证了所提出算法的聚类有效性。同时，对线性核KFCM算法与FCM算法聚类中心等价性证明提出反例，并对线性核KFCM算法与FCM算法等价性作了重新证明。由于Gauss核参数对于聚类算法的影响较大，下一步工作将对Guass核参数的恰当选取问题进行研究。

[1] Cortes C,Vapnik V.Support vector networks[J].Machine Learning,1995,20(3):273-297.

[2] Scholkopf B,Smola A J,Muller K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5):1299-1319.

[3] Filippone M,Camastra F,Masulli F,et al.A Survey of Kernel and Spectral M ethods for Clustering[J].Pattern Recognition,2008,41(1):176-190.

[4] 文传军,汪庆淼,詹永照.隐隶属度模糊C均值聚类算法[J].计算机应用与软件,2015,32(12),245-248.

[5] Girolami M.Mercer kernel based clustering in feature space[J].IEEE Trans on Neural Networks,2002,13(3):780-784.

[6] 张莉,周伟达,焦李成.核聚类算法[J].计算机学报,2002,25(6):587-590.

[7] 伍忠东,高新波,谢维信.基于核方法的模糊聚类算法[J].西安电子科技大学学报(自然科学版),2004,31(4):533-537.

[8] Zhang D Q,Chen S C.Fuzzy clustering using kernel method[C]//International Conference on Control and Automation,2002.Icca.Final Program and Book of.IEEE,2002:162-163.

[9] 于德亮,唐海燕,丁宝,等.基于粒子群优化模糊核聚类的电梯群交通模式识别[J].哈尔滨工业大学学报,2012,44(10):84-88.

[10] Niu Q,Huang X J.An improved fuzzy C-means clustering algorithm based on PSO[J].Journal of Software,2011,6(5):873-879.

[11] Kumar S,Singh S K.Hybrid BFO and PSO swarm intelligence spproach for niometric geature optimization[J].International Journal of Swarm Intelligence Research,2016,7(2):36-62.

[12] 王国胜.核函数的性质及其构造方法[J].计算机科学,2006,33(6):172-178.

[13] Verma H,Agrawal R K,Sharan A.An improved intuitionistic fuzzy c-means clustering algorithm incorporating local information for brain image segmentation[J].Applied Soft Computing,2016,46(C):543-557.

[14] Parastar H,Bazrafshan A.Fuzzy C-means clustering for chromatographic fingerprints analysis:A gas chromatography-mass spectrometry case study[J].Journal of Chromatography A,2016,1438:236-243.

GAUSS-INDUCEDKERNELFUZZYC-MEANSCLUSTERINGALGORITHM

Wen Chuanjun1Zhan Yongzhao2
1(SchoolofMathematicalSciencesandChemicalEngineering,ChangzhouInstituteofTechnology,Changzhou213002,Jiangsu,China)2(SchoolofComputerScienceandCommunicationEngineering,JiangsuUniversity,Zhenjiang212013,Jiangsu,China)

Aiming at the excellent nonlinear expression ability of the kernel fuzzy clustering algorithm, this paper proposes a Gauss-induced kernel fuzzy c-means clustering algorithm. Firstly, based on the kernel objective function and the gradient method, the central expression of the feature space clustering is obtained, and the kernel matrix expression of the cluster center and the sample is obtained by the inner product operation. Secondly, the kernel function in the kernel objective function is Gauss kernel function, and the input spatial clustering center expression is obtained by using the gradient method. Finally, the kernel matrix of the clustering center and the sample is substituted into the input space clustering center expression to get the new clustering center calculation method of GIKFCMs, and the corresponding GIKFCMs kernel clustering algorithm is obtained. In this paper, we studied the properties of GIKFCMs and analyzed the convergence and initialization constraints of the algorithm. The algorithm overcomes the shortcomings of the original kernel clustering algorithm in convergence and initialization constraints. The effectiveness of the proposed algorithm is verified by simulation experiments. In addition, this paper also corrects the error of linear kernel FCM and FCM algorithm equivalence.

Kernel method Fuzzy clustering Non-linear mapping Kernel clustering center Algorithm equivalence proof

2016-10-28。国家自然科学基金项目(61170126)；常州工学院校级课题(YN1305)。文传军，博士，主研领域：数据挖掘，模式识别，模糊聚类。詹永照，教授。

TP391.41

A

10.3969/j.issn.1000-386x.2017.08.046