基于资源分配指标的最大约束社区发现算法
2017-08-12宁念文许合利刘喜峰
宁念文 许合利 刘喜峰
1(河南理工大学计算机科学与技术学院 河南 焦作 454000)2(郑州工程技术学院机电与车辆工程学院 河南 郑州 450044)
基于资源分配指标的最大约束社区发现算法
宁念文1许合利1刘喜峰2
1(河南理工大学计算机科学与技术学院 河南 焦作 454000)2(郑州工程技术学院机电与车辆工程学院 河南 郑州 450044)
在复杂网络中的社区发现一直受到广泛的关注,基于模块度最大化的方法是目前流行的社区发现技术。提出一种基于资源分配(RA)指标和多步贪婪凝聚策略的模块度最大化社区发现算法RALPA(Resource Allocation-based of Label propagation Algorithm)。该算法利用准确衡量节点间相似性的RA指标,通过最大约束标记传播模型使社区内部节点拥有较高的相似性,与社区外部的节点拥有较低的相似性。然后,通过多步贪婪凝聚策略将划分模块度增加最大的多对小社区进行合并。实验结果表明,该算法不仅避免了对节点更新顺序的敏感和易得到平凡解的问题,而且提高了算法的稳定性和社区划分的精度。
社区发现 模块度最大化 资源分配指标 最大约束标记传播模型
0 引 言
社区结构具有内部个体之间联系密切,但与外部其他个体联系稀疏的特点。因此,根据“在具有社区结构的网络中,任何一个节点都应当与其大多数相邻节点在同一个社区内”的思想,2007年Raghavan[1]等提出了接近线性复杂度的大规模复杂网络社区发现算法—标签传播算法(LPA)。该算法具有简单高效、不需要提供社区规模和社区个数等先验知识的特点。但是,由于LPA在标签传播过程中存在着大量的随机性,这些随机性严重破坏了算法的鲁棒性,进而破坏了所识别社区结构的稳定性[2]。针对上述缺点,Barber[3]等为了避免算法将所有节点划分到同一社区,提出了一种带有约束的模块化标签传播算法(LPAm),将社区聚类问题转化为求基于模块度的目标函数最大值问题。但是,LPAm易陷入局部最优并且基于不同的社区具有相似的总节点度数。Liu[4]等提出了LPAm+算法,该算法在LPAm的基础上通过多步贪婪凝聚算法(MSG)使LPAm跳出局部最大值,提高了社区划分的精度。但是,该算法循环迭代效率较低,并且应用到大数据集上时性能受到限制。Leung等[5]发现算法经过5次迭代后,大部分节点已经正确聚集,后面的迭代主要是对社区内的节点进行不必要的更新。因此,通过改进LPA的节点更新策略和迭代规则可以提高算法的执行效率,减少迭代次数,使算法尽快收敛。
为了提高算法的迭代效率和划分社区的准确度,一方面通过节点影响力的优化,另一方面通过节点之间相似度的优化。张素智等[6]提出了基于节点聚集系数的分布式标签传播算法。该算法通过聚集系数衡量节点的影响力,使算法能够快速收敛到正确的社区中,同时通过并行化处理提高算法的执行效率。黄健斌等[7]提出基于相似性模块度最大约束标记传播算法。该算法将最大约束标记传播模型为目标函数,使划分的社区结构更加紧密。很多研究者通过网络拓扑结构中节点间的相似性衡量节点之间联系的强弱。周涛等[8]基于不同类型的网络对9种已知的基于局部信息的相似性指标在链路预测中的效果进行比较分析,并提出了资源分配指标RA(Resource Allocation index) 和LP(Local Path index)。通过在网络中的预测效果表明这种指标都具有明显好于9种已知指标的预测能力。
本文所做的工作:第一,利用RA相似性指标,使其准确地衡量直接相连节点间的相似性;第二,通过最大约束标记传播模型对网络进行粗粒度的社区发现,提高社区划分的准确度,避免算法对节点更新顺序敏感的缺点;第三,使用MSG算法依据模块度最大化策略合并已得到的社区结构,使算法得到更高质量的社区结构。
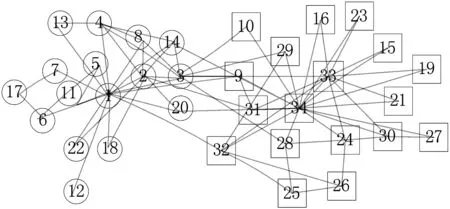
图1 Karate网络中社区结构特点
1 相关工作
现有的针对标签传播算法的改进都存在迭代次数增加导致算法性能降低或者是仍然存在较高随机性和不稳定性。本节通过资源分配指标准确衡量节点之间的相似性,减少标签传播过程中的随机操作和迭代次数。在基于节点之间的资源分配相似性和目标函数优化理论的基础上,通过最大约束标记传播模型判定标签的传播方向, 使社团的划分结果更加符合社团内部结构相对紧密, 社团之间结构较为稀疏的性质,提高算法对社区划分的精度。
1.1 标签传播算法基本步骤
网络G=(V,E),V表示节点集,E表示边集。对于任意的x∈V,Cx(t)=Lx。Cx(t)表示t时刻节点x所属的社区,Lx表示x节点t时刻的标签。LPA算法的具体步骤如下:
(1) 每个节点初始化唯一的标签Lx=x。
(2) 将V中节点随机重新排序,并赋予节点集x。
(3) 对于重新排序后的任意x∈X,节点x将自身的标签更新为其邻节点中拥有相同标签节点个数最多的标签。
(4) 当所有节点的标签都与其大多数相邻节点的标签相同时,算法结束。否则,继续返回第2步再次进行标签的更新。
标签的更新策略分为:同步更新策略和异步更新策略。同步更新策略是当对节点进行第t+1次标签更新时,依据邻居的第t次标签来更新自身的标签。异步更新策略是对节点进行第t+1次更新时,依据邻居最新的标签来更新自身的标签。由于同步更新策略容易产生震荡现象,所以本文算法采用异步更新策略。
1.2 资源分配指标(RA)
为了更加准确地衡量节点间的相似度,我们利用RA指标相似性反映节点之间联系的紧密程度。在图1中节点12.0和节点1.0直接相连。那么,根据文献[8]中RA的定义不能够直接计算,文献[9]计算得到两点之间的相似性为0,将节点12.0和不在节点1.0邻域中的其他节点同等对待,这样导致衡量的结果不够准确,不能正确反映节点之间的关系。因此,本文对RA相似性进行了扩展:
(1)
x和y直接相连, 表示节点x和节点y之间的相似性, 表示x的邻接点集(包括x节点本身以及与x直接相连的节点),k(z)表示x和y共享的邻节点集中节点z的度数。扩展之后的RA相似性能够更加准确地反映节点之间的相似性,将相邻节点之间的相似性与非相邻节点进行了区分。
1.3 最大约束标记传播模型
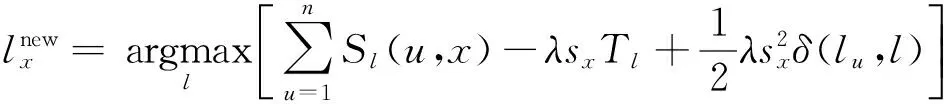
(2)
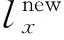
本文基于RA指标和最大约束标记传播模型对网络进行粗粒度的社区发现。因为RA指标能够通过节点局部信息准确地反映节点之间联系的紧密程度,所以使最大约束标记传播模型能够提高社区划分的准确度,并且使划分结果更加符合社区结构的特点。
2 RALPA算法
2.1 RALPA算法思想
本文提出的RALPA算法主要分为两个部分:1) 通过RA相似性的最大约束标记传播模型进行社区发现,得到粗粒度的社区划分;2) 在上一步划分的基础上,进行基于MSG算法的模块度最大化社区的修正。
MSG算法的对于社区对的修正准则为:假设t1和t2是要合并的社区对,合并后模块度增加量为ΔQ(t1,t2)并且不存在其他任意的社区t,与t1、t2组成社区对(t,t1)或(t,t2),使ΔQ(t,t1)、ΔQ(t,t2)>ΔQ(t1,t2)。通过两种方式的结合,随着迭代次数的增加,能够更快、更准确地将节点划分到正确的社区中。同时,减少模块度最大化合并的社区数目和在局部最优空间中的小范围循环次数,避免低效率的迭代。
RALPA算法的主要思想:首先,利用RA指标计算每个点与相邻节点之间的相似性;然后,根据最大约束标记传播模型来更新节点的标签,得到初步的社区划分结果;最后,基于MSG算法合并能够使社区模块度最大程度提高的社区,得到最终的社区划分。因为文献[5]中经过大量实验证明经过5次迭代后,95%的节点已正确的聚集。所以,本文设置算法的迭代次数为5次。因为通过MSG算法对结果进行修正,所以能够同时合并多对符合要求的社区,提高算法的效率。
算法1 RALPA算法
输入:网络G=(V,E),V表示节点集,E表示边集,迭代次数Iterate=5
输出:各节点以及所属的社区
变量和函数说明:
ΔQt1t2表示社区t1和t2合并之后模块度的变化量;Initialize(x)表示节点x的标签初始化;Merge(t1,t2)表示将社区t1和t2进行合并。
算法流程:
1) 初始化每个节点的标签Vi=i。
2) 计算每个节点x的邻域Γ(x),根据式(1)计算每个节点x与其他节点y的资源分配相似性矩阵Sxy。
3) 迭代次数iter=1。
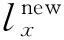
5) 如果每个节点的标签都不再变化或者达到最大迭代次数Iterate,则算法结束,具有相同标签的节点为同一个社区;否则iter=iter+1,返回步骤(4)。
6) 在步骤5)所得到结果的基础上,根据MSG算法合并准则,同时合并使模块度增大的多对社区。
7) 如果任意社区对合并后模块度不再增加,那么算法结束;具有相同标签的节点为同一个社区。
算法伪代码:
For everyx∈V
xlabel= Initialize(x);
//将节点的标签初始化
Fory∈xneighbor
//依次计算x和邻域元素的相似度
// Sxy表示节点之间的相似矩阵
End for
End for
For iter=1:Iterate
//设置最大迭代次数
For everyx∈V
//根据下面公式更新节点自身的标签
End for
End For
While ∃(t1,t2):Δt1t2>0
//模块度增加量为正整数
For every (t1,t2):Δt1t2>0∧!∃t:Δt1t>Δt1t2∨Δt1t<Δt1t2
Merge(t1,t2);
//合并社区对
End For
End While
2.2 时间复杂度分析
对于图G=(V,E),N表示节点个数,M表示边的个数,最大迭代次数Iterate。本文算法主要的时间复杂度为节点标签更新的时间复杂度和计算社区划分模块度的时间复杂度。
节点标签更新的时间复杂度为:对每个节点进行相似性计算和更新标签的时间复杂度为O(N);Iterate次迭代的总时间复杂度为O(Iterate×N)。
计算模块度的时间复杂度:每次计算模块度增量计算的时间复杂度为O(M);以模块度优化为目的进行社区之间的合并所需要的最大时间复杂度为O(N),社区合并在最坏情况下需要的迭代次数为O(logN)。因此,RALPA算法的时间复杂度为O(M×logN)。由于采用基于相似性的社区发现和MSG凝聚策略所以比LPAm+算法拥有更优的时间复杂度。
3 实验结果与分析
在真实网络数据集和人工网络数据集上,通过模块度和NMI值,这两种公认的评价标准来验证算法的性能。本文所采用的数据集:1)真实网络数据集,数据来源于现实世界中,通过对真实世界中关系的建模得到;2)人工网络数据集,即利用程序自动生成的数据集。本文采用LFR基准程序生成人工网络数据集。本文算法的实验环境为Matlab2014a软件,硬件的配置为:Pentium(R) Dual-Core CPU, E5800 @ 3.20GHz, RAM 4.00G;软件配置:64位WIN8操作系统。
3.1 模块度Q
Newman和Girvan在文献[10]中提出模块度的概念,后来作为衡量社区算法性能的公认评价标准。模块度用来衡量社区结构性的强弱,其值越接近1,表示划分出的社区结构性越强,划分的结果越好。模块度的定义如下:
(3)
其中,N表示社区数目,lc表示社区c中的总边数,m表示网络中的总边数,dc表示社区c中节点度数的总和。
3.2 标准化互信息NMI
NMI[11]即标准化互信息,通过NMI值比较社区划分的结果与标准社区结构的相似度,从而衡量社区划分的质量。由于本文采用的真实网络数据集的社区结构已知,以此衡量划分结果与真实社区的相似度。NMI的定义为:
(4)
其中,Ni,j表示两个社区公共节点数,Ni和Nj分别表示混合矩阵中第i行与第j列的和。
3.3 真实数据集
为了验证本文提出的RALPA算法的性能,选择的真实数据集为空手道俱乐部Karate数据集、海豚Dolphins数据集、橄榄球俱乐部Football数据集、政治书Polbooks数据集四种公认的真实网络数据集,其参数如表1所示。
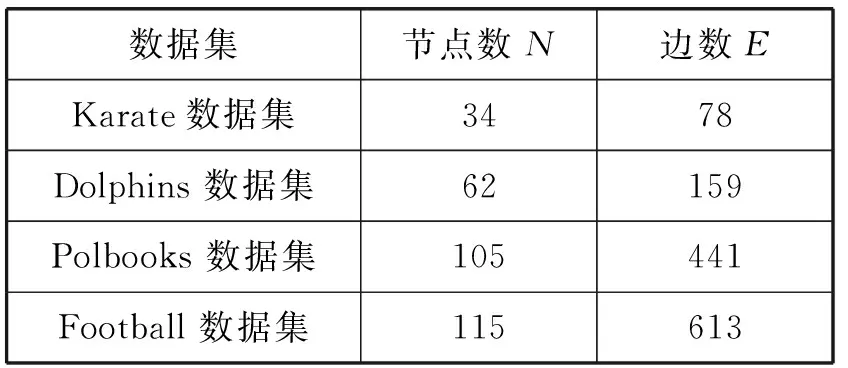
表1 真实网络数据集信息
将算法应用到真实网络数据集测试所划分社区的平均模块度Q和NMI指标。将本文算法与传统LPA、LPAm、LPAm+、MLPA进行比较。不同算法分别在四种数据集上进行100次运算,计算结果的平均模块度和NMI值见表2和表3。
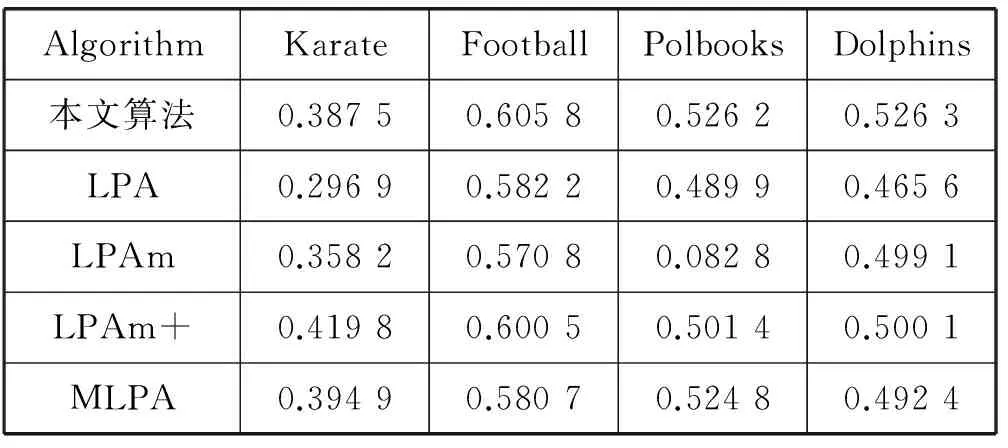
表2 各种算法平均模块度的比较
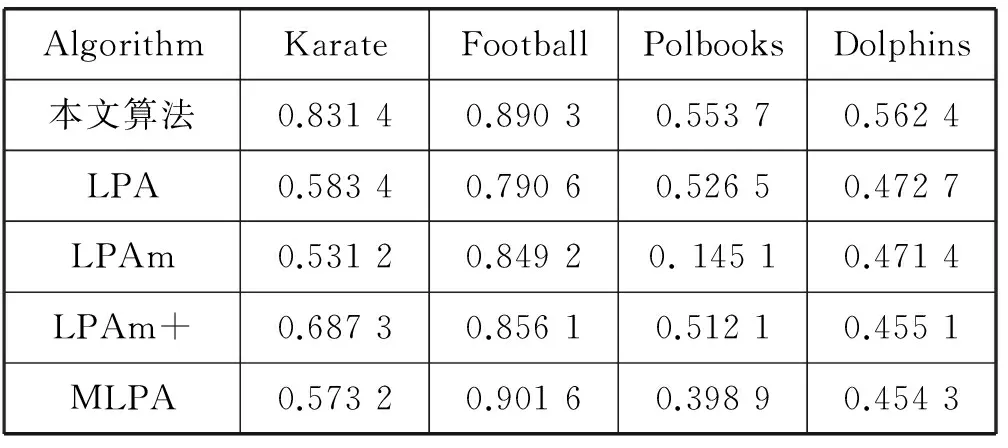
表3 各种算法NMI值的比较
通过对表2和表3的分析可知,RALPA算法在四种不同的真实数据集中表现出较好的性能。但在Karate数据集中本文算法的平均模块度值不是最好。由于LPAm+算法从初始节点开始进行模块度的优化,所以获得了很好的模块度,同时导致算法具有较高的时间复杂度。总体而言,本文算法表现出较好的性能,特别是在Polbooks社区结构不明显的情况下也获得了较好的结果。本文算法对karate数据集的划分结果如图2所示。
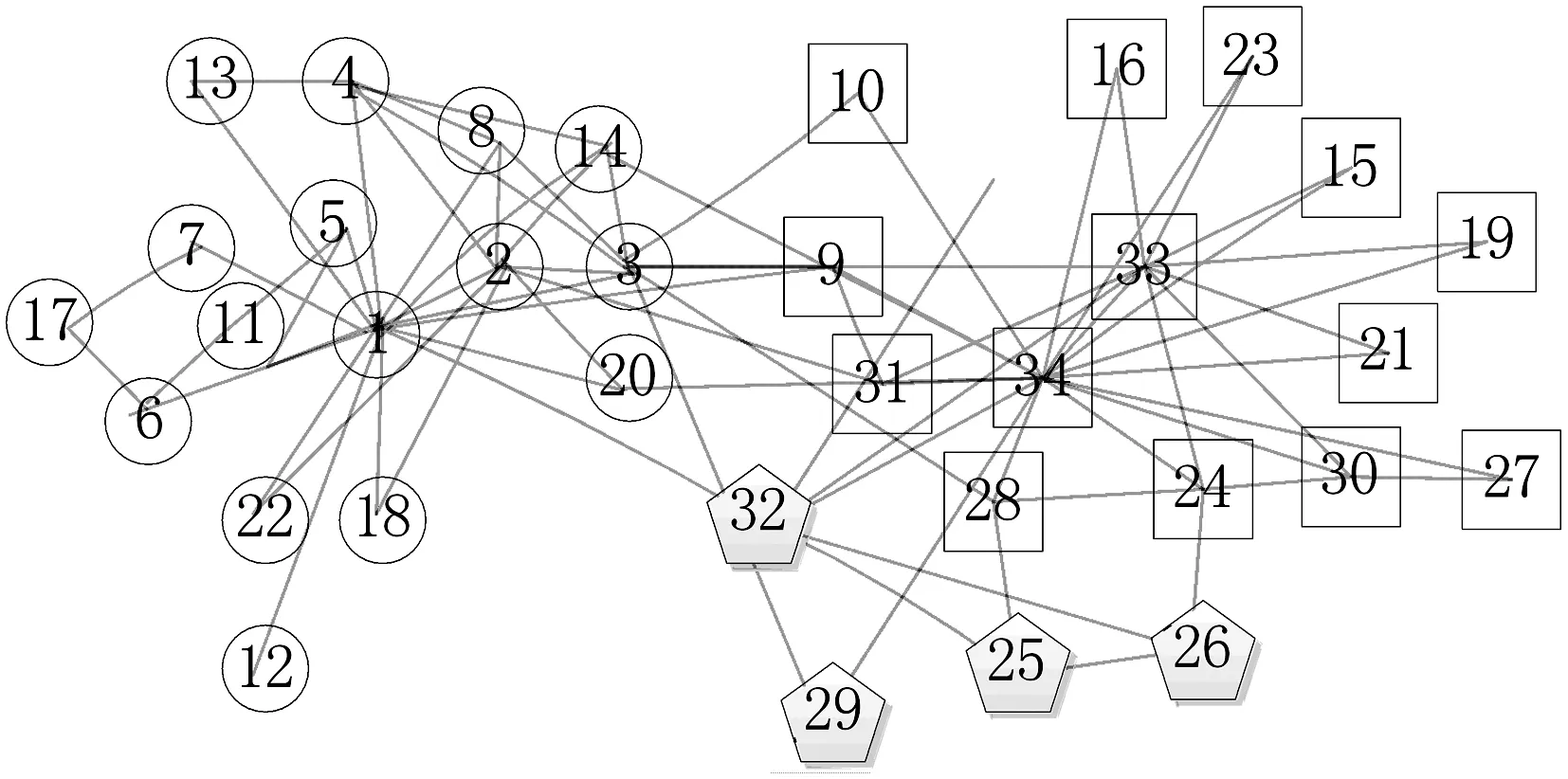
图2 本文算法对Karate数据集划分结果
通过图1与图2的对比,本文算法将以33.0为中心的社区划分为两部分。其中{25.0,26.0,29.0,32.0}表示一个小社区,这样使获得的社区结构具有较高的模块度。这四个节点在最大约束标记传播模型和模块度最大化两者作用下,最终获得了具有更高模块度的社区划分。综上所述,RALPA算法在4个真实网络数据集中得到了较好的社区结构。
3.4 LFR人工网络数据集
通过LFR基准程序分别生成了500个节点基准数据集和1 000节点的基准数据集。节点数N,平均度数AD, 最大度数MD, 最大社区规模MXC, 最小社区规模MIC,节点度分布指数DD, 社团规模分布指数DC, 社区混合参数μ。其中,μ表示混合参数,反映生成社区结构性的关键指标。具体信息如表4所示。
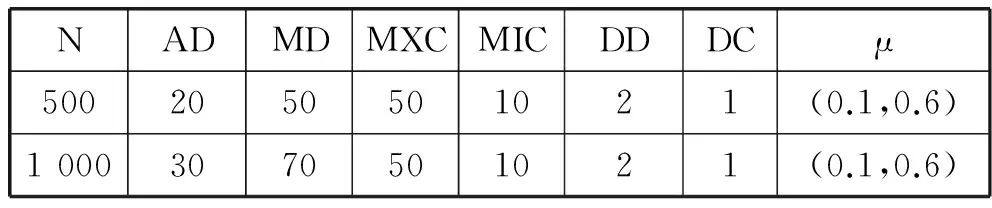
表4 两种LFR网络参数信息
LFR人工数据集已有确定的社区结构,在这两种数据集上通过分析NMI值比较算法的性能,考虑到实验中算法的不稳定性,不考虑结果为0的样本。实验结果如图3(a)、(b)所示。
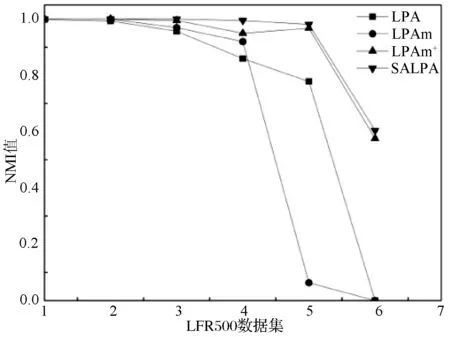
(a) 算法在LFR500数据集上NMI值
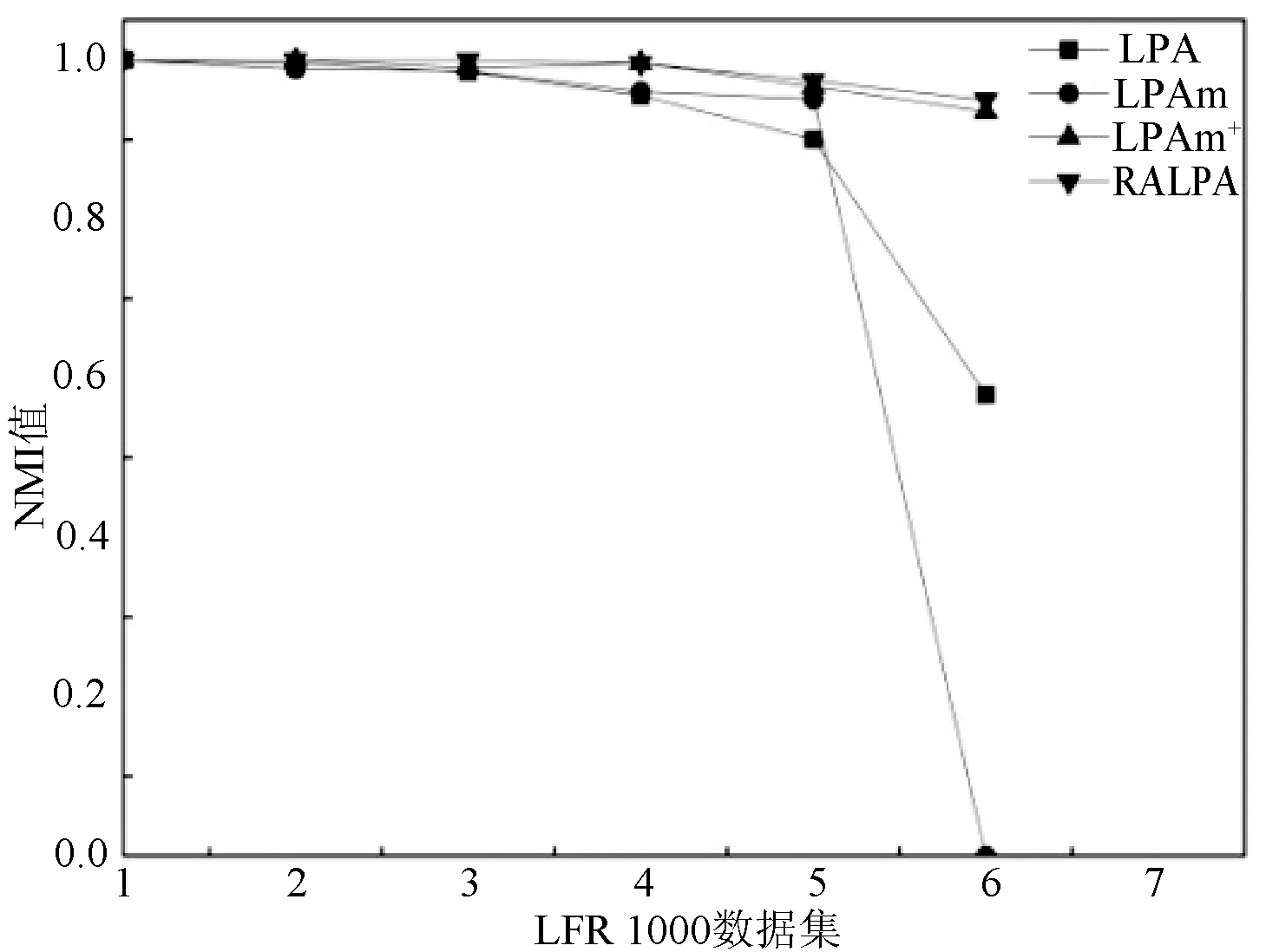
(b) 算法在LFR1000数据集上NMI值图3 4种算法分别在两种数据集上的NMI值
在节点为500和1 000的人工网络数据集中,RALPA算法表现出较好的性能,划分出更准确的社区结果。其中,在μ≤0.6时,社区结构不明显的情况下能表现出比LPA、LPAm、LPAm+算法更好的性能。无论是在500个节点的数据集中还是1 000个节点的数据集中,本文算法划分结果的NMI值都在0.60以上。表5为本文算法和MLPA算法在μ=0.6和μ=0.65时的NMI结果比较,可以看出本文算法在社区结构不明显的情况下优于MLPA算法。由于RALPA算法具有较低的时间复杂度和较好的划分结果,所以本文算法比以上算法具有更好的性能。
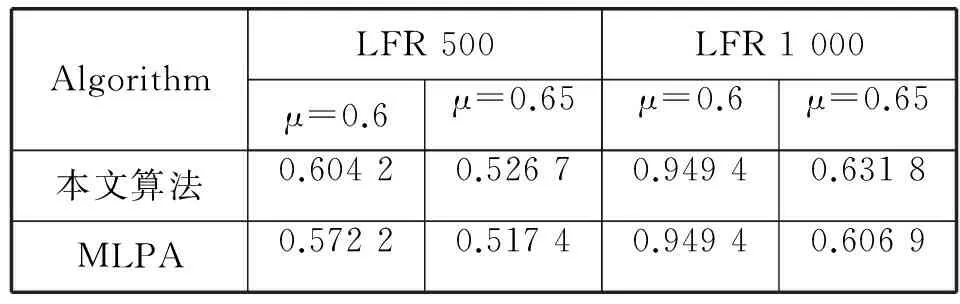
表5 社区结构不明显的情况下算法NMI值的比较
4 结 语
RALPA算法利用资源分配指标更准确地衡量节点之间的相似性。通过引入最大约束标记传播模型,使划分出的社区结构内部节点之间具有更高的相似性,与社区之间具有较低的相似性,提高了社区划分精度,减少了在局部最优取值空间中的迭代次数。通过多步贪婪凝聚算法进行模块度最大化,提高了社区合并的效率,同时使算法能够跳出局部最优解。通过在真实基准数据集和人工网络数据集的实验结果表明RALPA算法具有更好性能,能够划分出更高质量的社区结构。
本文算法运用模块度最大化进行社区发现,但是由于模块度的缺陷使以模块度为目标函数的优化算法只能够发现特定的社区结构,而真实网络中的社区都是多规模的。因此,下一步的工作是对多分辨率社区发现算法的研究。
[1] Usha Nandini R, Réka A, Soundar K. Near linear time algorithm to detect community structures in large-scale networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007,76(3):36106.
[2] 石立新, 张俊星. 一种稳定的标签传播社区发现算法[J].计算机应用与软件, 2015,32(3):261-265.
[3] Barber M J, Clark J W. Detecting network communities by propagating labels under constraints[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009,80(2):283-289.
[4] Liu X, Murata T. Advanced modularity-specialized label propagation algorithm for detecting communities in networks[J].Physica A: Statistical Mechanics and its Applications, 2010,389(7):1493-1500.
[5] Leung X Y, Hui P, Lio P, et al. Towards real-time community detection in large networks[J].Physical review E, Statistical, nonlinear, and soft matter physics,2009,79(6):066107.
[6] 张素智, 孙嘉彬, 王威. 基于节点聚集系数的分布式标签传播算法[J].计算机应用与软件,2016,33(4):125-128.
[7] 黄健斌, 钟翔, 孙鹤立,等. 基于相似性模块度最大约束标记传播的网络社团发现算法[J]. 北京大学学报(自然科学版),2013(3):389-396.
[8] Zhou T, Lü L, Zhang Y C. Predicting missing links via local information[J].The European Physical Journal B, 2009,71(4):623-630.
[9] Pan Y, Li D H, Liu J G, et al. Detecting community structure in complex networks via node similarity[J].Physica A:Statistical Mechanics and its Applications,2010,389(14):2849-2857.
[10] Newman M E. Fast algorithm for detecting community structure in networks[J].Physical review. E, Statistical, nonlinear, and soft matter physics, 2004, 69(6):066133.
[11] Danon L, Diaz-Guilera A, Duch J, et al. Comparing community structure identification[J].Journal of Statistical Mechanic:Theory and Experiment, 2005(9):P09008.
MAXIMUM CONSTRAINED COMMUNITY DETECTION ALGORITHM BASED ON RESOURCE ALLOCATION INDEX
Ning Nianwen1Xu Heli1Liu Xifeng2
1(CollegeofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)2(InstituteofElectricalandMechanicalVehicleEngineering,ZhengzhouInstituteofTechnology,Zhengzhou450044,Henan,China)
Community detection in complex networks have
wide attention, and the method based on modularity maximization is the popular community detection technology. In this paper, a modularity maximization community detection algorithm named RALPA (Resource Allocation-based of Label Propagation Algorithm) is proposed, which is based on resource allocation (RA) and multi-step greedy cohesion strategy. The algorithm uses the RA index to measure the similarity between nodes accurately. By using the maximum constraint label propagation model, the internal nodes of the community have high similarity, and have low similarity with the nodes outside the community. Then, through the multi-step greedy cohesion strategy, the multi-pair small communities with the largest increase of partitioning degree will be merged. The experimental results show that the proposed algorithm not only avoids the problem of the sensitivity of node update order and the trivial solution, but also improves the stability of the algorithm and the accuracy of community division.
Community detection Modularity optimization Resource allocation Maximum constraint label propagation model
2016-07-11。国家自然科学基金项目(61202286);国家科技重大专项核心电子器件、高端通用芯片及基础软件产品专项(2014ZX01045-102)。宁念文,硕士生,主研领域:数据挖掘,并行计算。许合利,教授。刘喜峰,教授。
TP3
A
10.3969/j.issn.1000-386x.2017.07.040
