基于统计分析的自适应蚁群算法及应用

许明乐 游晓明* 刘 升

1(上海工程技术大学电子电气工程学院 上海 201620)2(上海工程技术大学管理学院 上海 201620)



基于统计分析的自适应蚁群算法及应用

许明乐1游晓明1*刘 升2

1(上海工程技术大学电子电气工程学院 上海 201620)2(上海工程技术大学管理学院 上海 201620)

路径规划是机器人关键技术之一。利用改进的蚁群算法进行机器人的路径规划。针对传统蚁群算法收敛速度慢且易陷入局部最优解的缺陷，在Ant Colony System算法基础上，对每代蚁群动态随机统计分析，提取最优、平均和最差的蚂蚁信息，构成自适应算子用于局部信息素的自适应更新。仿真实验结果证明该自适应算子在平衡增加收敛速度和陷入局部最优解矛盾的问题中是有效的。

路径规划 自适应精英策略 统计分析 蚁群算法

0 引 言

移动机器人技术是机器人技术的重要组成部分，应用前景十分广阔，可广泛应用于工业、农业、国防、医疗、以及服务业等[1]。文献[2]提出未来数年内，中国服务机器人发展将超过传统的工业机器人。机器人路径规划技术是服务机器人研究的核心内容之一[3]，研究机器人的路径规划问题十分必要。

近年来，各国学者致力于机器人路径规划的研究且取得了相当丰硕的研究成果。目前已有多种算法用于规划机器人的路径，文献[4]将其分为经典方法和进化算法。进化算法等人工智能技术是近些年来新兴的技术，有着传统方法不具有的优点，它使得移动机器人在理论上拥有了一定的“智能”。

进化算法中的蚁群算法是人工智能技术的组成部分，最早由意大利学者Dorigo于20世纪90年代提出AS(ant system)，首先成功应用于解决TSP问题[5]。蚁群算法是一种拥有自组织和正反馈优点的并行优化算法，经过学者们大量研究，成功运用于许多领域[6]。

然而，和其他算法一样，蚁群算法也面临着一些挑战，一个有效的启发式算法必须要实现对还未探索过领域的探索和对当前已获得结果的开发之间的平衡，改善路径上信息素的更新方式是实现这种平衡的方法之一[7]。文献[5]提出精英蚂蚁的概念，在基本的信息素更新的基础上，额外增加了最优路径上信息素增量，以提高收敛速度。然而精英蚂蚁的增加，使得最优路径上信息素快速增加，降低了种群多样性。文献[8]根据每代中不同蚂蚁的结果得到不同的信息素增量，可以避免精英蚂蚁的影响。在提高收敛速度的同时，通过减少最优蚂蚁与次优蚂蚁路径上信息素的差距来增加种群多样性。但是此方法仅使用了部分蚂蚁的信息，无法体现群体智能行为。文献[9]提出局部更新信息素的方法，通过减少已访问边上的信息素量来鼓励后续蚂蚁选择其他的边，以提高种群多样性。然而，局部信息素的更新是一个定值，每一代蚁群之间相同，不能表现蚁群算法作为群智能算法的进化智能。

蚁群算法作为一种正反馈的群智能算法，应当积极使用群体所表现的智能行为，以提高蚁群算法的性能。本文在局部更新的基础上，对每一代蚁群进行统计分析，利用整个蚁群的信息以提高种群多样性，对蚁群中不同蚂蚁统计分析进行不同的信息素更新以提高收敛速度。根据每一代蚂蚁的不同结果还可以自适应地调整蚁群迭代过程，以体现蚁群的群体智能行为。

1 机器人路径规划问题和环境建模

机器人的路径规划是指按照一定的性能指标搜索一条从起始状态到目标状态的最优或近似最优的无碰路径[14]。按照机器人对环境信息已知程度的不同，路径规划问题分为对环境已知的全局路径规划和对环境信息完全不知或者部分不知的局部路径规划问题[7]。前者在已知或者直接给出的静态环境中进行相关的工作，本文进行的就是机器人全局路径规划研究，即障碍地图已知的机器人路径规划研究。

对于机器人的环境建模有多种方法，如可视图法、maklink和人工势场法等。其中栅格法是一类经典的环境建模方法，本文采用此种方法对环境进行建模，将环境划分为单位大小的正方格，如果方格内有障碍物，则标记为1，在图形中表示为黑色；没有障碍物的方格标记为0，在图形中表示为白色。在计算中用方格的中心表示方格的整体位置。在四周没有障碍、也不是边缘方格的前提下，每个方格有8个方向可以移动，即右、右上、右下、左、左上、左下、和正上和正下八个方向可以移动。

2 相关工作

从自然界中蚂蚁寻求蚁穴到食物之间的最短路径得到启示，20世纪90年代Dorigo.M最早提出蚂蚁算法AS，主要基于搜索过程中信息素的正反馈机制和启发式的贪婪机制，首先成功运用于NP难中的TSP问题。根据算法优点，蚁群优化算法成功运用于很多问题[12-14]。与此同时，蚁群算法也开始应用于机器人路径规划。

在基本蚁群AS的基础上，本章介绍了几类经典的改进算法，分别是精英蚁群算法(ASelite)，排序蚁群算法(ASrank)，和蚁群系统(ACS)。

2.1 基于精英策略的蚁群算法(ASelitist)

根据基本的蚁群优化算法，精英策略改进了信息素的更新方式[5, 13]。主要思想是：每一次迭代中全局最优蚂蚁所经过的路径，获得额外的信息素更新，相当于好几只蚂蚁经过了此最优路径并释放了信息素。这加强了全局最优蚂蚁对后续蚂蚁的影响，使后面的蚂蚁在全局最优路径及其附近的路径上的选择概率增加，在当前最优的路径上进一步的开发，提高了算法的收敛速度。

精英策略蚂蚁系统中信息素更新规则按下式计算：

τ(i,j)←(1-ρ)τ(i,j)+△τ(i,j)+△τ(i,j)*

(1)

(2)

式中，σ为精英蚂蚁的数量，L*为全局最优路径的长度。

实验结果表明基于精英策略的蚂蚁算法提升了蚂蚁算法收敛速度[5]。但是，随着精英蚂蚁对应路径上信息素的增加，降低了后续蚂蚁解的多样性。单纯的精英算法牺牲了算法的多样性来提升收敛速度。其潜在的缺陷和遗传算法中保留最优个体的行为类似，造成算法的早熟，使得某一条路径上的信息素急剧增加，从而严重影响了后续蚂蚁解的多样性，使得算法收敛于某一局部最优解[17]。

作为群智能进化算法，精英策略虽提高了种群中最优个体的作用，但忽视了每一代蚂蚁中较优个体的智能行为，没体现种群进化的特点。

2.2 基于排序策略的蚁群算法(ASrank)

考虑到精英策略的缺陷，联系到遗传算法中对个体适应度排序并进行选择的策略，Bullnheimer·B等提出了基于排序的精英蚂蚁算法，它只更新一定量较优蚂蚁路径上的信息素[8]。此算法改进后的信息素更新策略按照下式进行：

τ(i,j)←ρ·τ(i,j)+△τ(i,j)+τ(i,j)*

(3)

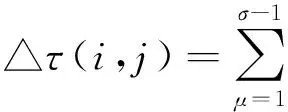
△τ(i,j)μ=

(4)

式(3)中τ(i,j)*是全局最优路径上信息素更新的增量，是保留了精英策略的部分，也按照式(2)进行计算。

排序策略不仅增加了最优路径上的信息素增量，还增加了次优路径上的信息素增量。相对于精英蚂蚁算法，排序策略提高了后续蚂蚁解的多样性，即后续蚂蚁在路径转移中的指导不仅仅来自于全局最优蚂蚁，还有历次迭代中前几只较优的蚂蚁。排序策略保留了精英策略让当前最优的蚂蚁指导后续蚂蚁解的构造过程，但更进一步地考虑了每代蚂蚁中较优个体的智能行为，并且还考虑了优化程度不同蚂蚁之间的差别，即给予不同的权重。正如文献[8]所说排序策略通过选择多个较优个体的方法来减少精英策略或者是全局优化策略带来的潜在缺陷。实验结果表明排序策略有一定的效果。

排序策略使用更多的蚂蚁信息缓解了精英策略的弊端，可见考虑更多蚂蚁的信息有利于解决蚁群算法中收敛速度和解的多样性之间的矛盾，这体现了排序策略的有效性。然而，排序策略仅仅考虑了每一代蚂蚁中较优个体的信息，忽视了每一代蚂蚁的整体信息。此外，虽然排序策略考虑了较优蚂蚁之间的不同，但是却没有考虑到较优蚂蚁与其他不执行更新操作蚂蚁之间的不同，如最后一只较优蚂蚁和第一只非较优蚂蚁之间的差异很有可能极小，这种情况下，更新前者而不更新后者是有一定缺陷的。考虑每一代蚂蚁的所有信息将有助于算法性能的进一步提高。

2.3 蚁群系统(ACS)

针对基本蚁群算法的缺陷，ACS是一类经典的改进算法[11]。相对于基本蚁群算法，ACS主要对状态转移规则和信息素更新方式做了如下改变：

在状态转移过程中，利于伪随机概率选择下一城市，即位于城市i的蚂蚁在选择下一城市时按照下式进行：

(5)

通过伪随机的不确定性，改变了AS中选择路径的规则和信息素和启发式之间的确定性关系，增加了蚂蚁在求解过程中解的多样性，从而增加跳出局部最优解的可能性。

ACS算法有全局信息素更新和局部信息素更新两个部分。局部信息素的更新利用了每一代蚂蚁的路径信息，一定程度上提高了算法多样性。但是路径对应的信息素增量都相同，每一代增量也相同，没有考虑不同蚂蚁的信息，也无法体现群体进化的特点。

ACS中全局信息素更新规则根据下式进行：

τ(i,j)←(1-α)·τ(i,j)+α·△τ(i,j)

(6)

式中：

全局信息素更新的是当前所有迭代中出现的全局最优解对应路径上的信息素。与此同时，文献[11]也提出了当代最优的概念，相对于全局最优解，当代最优路径上信息素的更新得到的实验效果稍差于全局最优。全局最优路径上信息素的增强，指导了后面蚂蚁解的构造过程，使得当前最优解对应路径上的邻近路径在此后得到进一步的开发，增加了收敛速度。在全局最优和当代最优的选择中，根据实验结果作者选择了前者，然而作者却忽视了当代最优的信息。正如文献[11]所说，全局最优只是比当代最优的效果稍微好一点，将两者同时使用有可能进一步的提高算法的性能。

3 基于统计分析的自适应精英蚁群算法

蚁群算法是一种随机搜索方法，与遗传算法类似，主要用在大量的可能解中寻求最优解。蚁群算法解的构造主要包括两部分，其一是通过每个个体单独构造解，其二是群体之间的信息交流。个体蚂蚁的行为虽然简单，但是作为一个群体而体现出相应的智能。蚁群算法通过信息素的改变，充分地发挥了个体蚂蚁与群体之间智能行为。

然而实际上，以上改进算法都忽视了整个群体蚂蚁的智能行为，要么只是利用了部分蚂蚁的信息，或者是没考虑迭代过程中蚁群的进化。由第2节分析，如果利用蚁群算法作为进化算法的特征，以及每一代蚁群的信息，则可以提高种群多样性。

但是，如果直接利用所有蚂蚁的所有信息，最优个体的信息的作用会被相应的降低，进而使得算法的收敛速度下降；还会由于信息交流量增加，算法的复杂度也会增加。因此本文寻找一种利用群体信息而又不会影响算法其他性能的方法。

统计学中利用均值等概念来表示一个群体的相关特征信息。本文借鉴统计分析的方法提取了每一代蚁群的三个特征参数，即在最优值的基础上，本文还提取了每代蚂蚁信息的均值和最差的值来代表这一代的蚂蚁信息，进而在蚁群的信息交流(信息素更新)中加以利用。

本文在ACS算法基础上借鉴精英策略和排序策略，加入本文提出的自适应算子。得到的局部信息素更新方式按照下式进行：

τ(i,j)←(1-ρ)·τ(i,j)+ρ·△τ(i,j)

(7)

式中ρ为可调参数，而△τ(i,j)按下式计算：

△τ(i,j)=

(8)

式中，σ为精英蚂蚁的个数，为可调参数，Lk为每一代中最优蚂蚁对应的最短路径长度，Lwor为每代中最差蚂蚁对应的路径长度，L为每代中除去最优蚂蚁的其他σ-1个较优蚂蚁对应的路径长度，Lave为每代蚂蚁的平均路径长度。

本文引用了ACS中全局信息素更新策略，本文全局信息素更新策略按照下式进行：

τ(i,j)←(1-α)·τ(i,j)+α·△τ(i,j)*

(9)

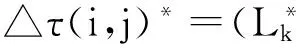
另外，根据机器人路径规划的实际问题，本文引用文献[18]启发式方法，即当前节点到下一节点的启发式信息是下一节点到目标节点的欧式距离。启发式信息按照下式生成：

eta(j)=distance(j,goal)

(10)

式中，eta(j)表示节点j的启发式信息，distance(j,goal)表示节点j到节点goal之间欧式距离，goal是机器人路径规划的目标结点。

4 实验结果与仿真

为了验证本文改进算法的有效性，本节将本文算法和精英蚂蚁算法、排序蚁群算法及蚁群系统分别应用于栅格法的机器人路径规划仿真实验中。仿真实验在MATLAB中进行：3.3 GHz处理器，内存4 GB，32位系统。

4.1 简单环境下四种算法的性能比较

本文首先将各种算法运用于不同的简单障碍环境下进行路径规划，各种环境下的参数设置见表1所示。起点从障碍图的左上角开始计数，从左到右，从上到下依次增加。

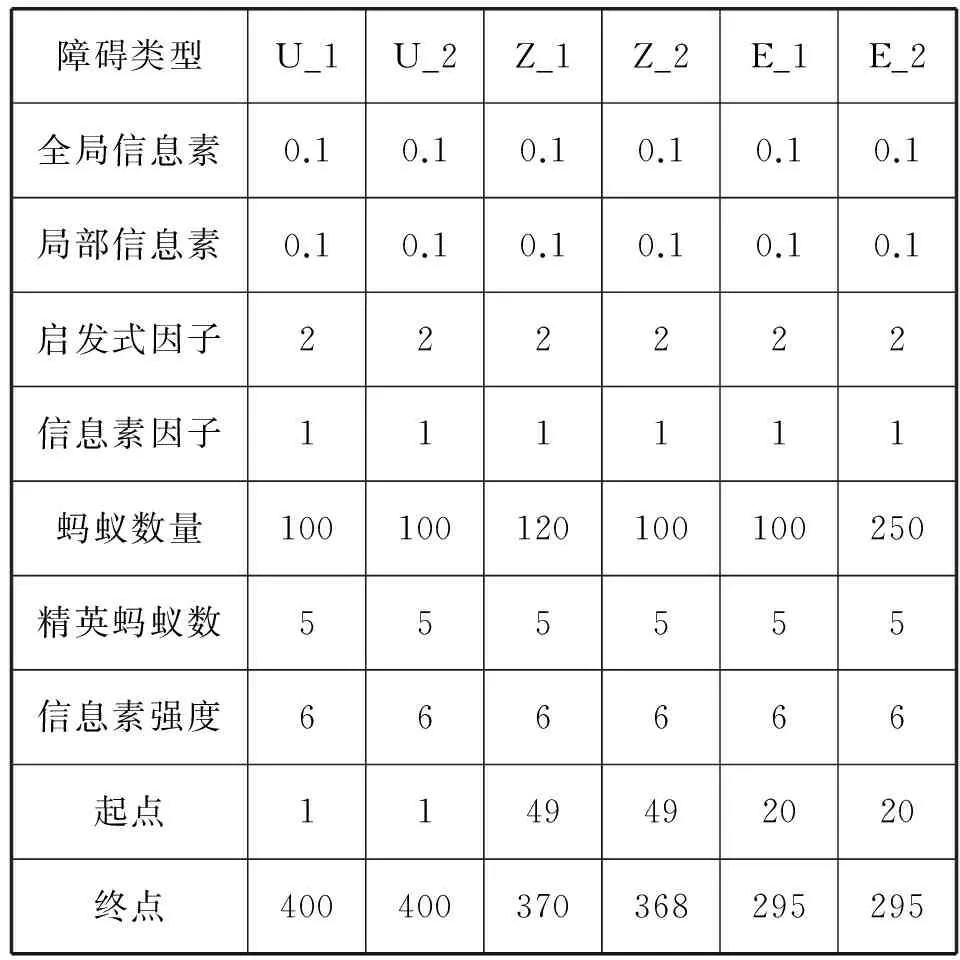
表1 不同环境下算法的参数设置情况

图1和图2分别给出了都为U型障碍物环境但障碍物位置不同时四种算法的路径规划情况和迭代曲线图。从中可以看出，当U型障碍物在右边时，四种算法都能很快地找到最优路径，各种算法并没有太大区别。但是一旦U型障碍物在左边时，此时启发式的理想路径经过U型障碍物的内部，情况则变得不一样。ACS收敛速度最快，但是本文算法得到了最优解，相应的收敛速度也并不慢。除了本文算法，其他算法都未能找到最优解。

从图3和图4看出，即使在同一障碍物下，即使起点相同，而终点不同时，路径规划的难度也是不一样的。当终点在障碍物交接中间时，ACS算法和本文算法都能够找到最优解，但本文的收敛速度明显要快于ACS算法，而精英蚂蚁和排序蚂蚁算法并没有找到最优路径。当终点位于障碍物交界的左边时，排序算法和精英算法几乎始终在距离终点最近的点处徘徊，无法找到新的出口，其多样性明显比较差。而ACS算法虽然在前几次都能够逃离局部最优解，然而，在最后一个可能局部最优解中没能成功逃离，其多样性还有待进一步提高。虽然ACS算法收敛速度最快，但是本文算法并没有下降很多。本文算法在较困难的路径规划中仍然可以较快地找到最优解而不陷入局部最优。

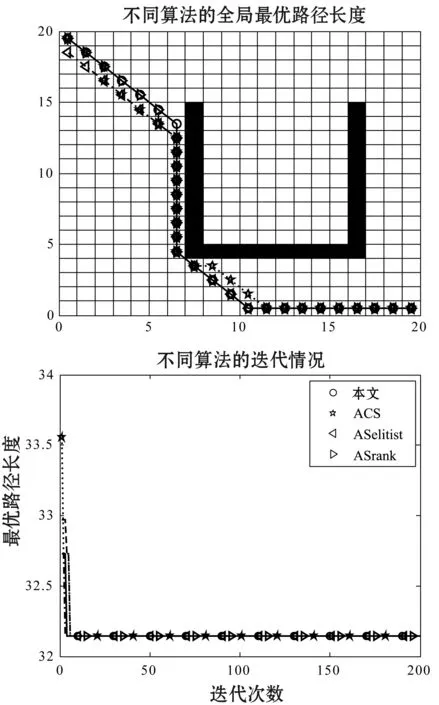
图1 U_1·右边U型障碍物路径规划和迭代情况

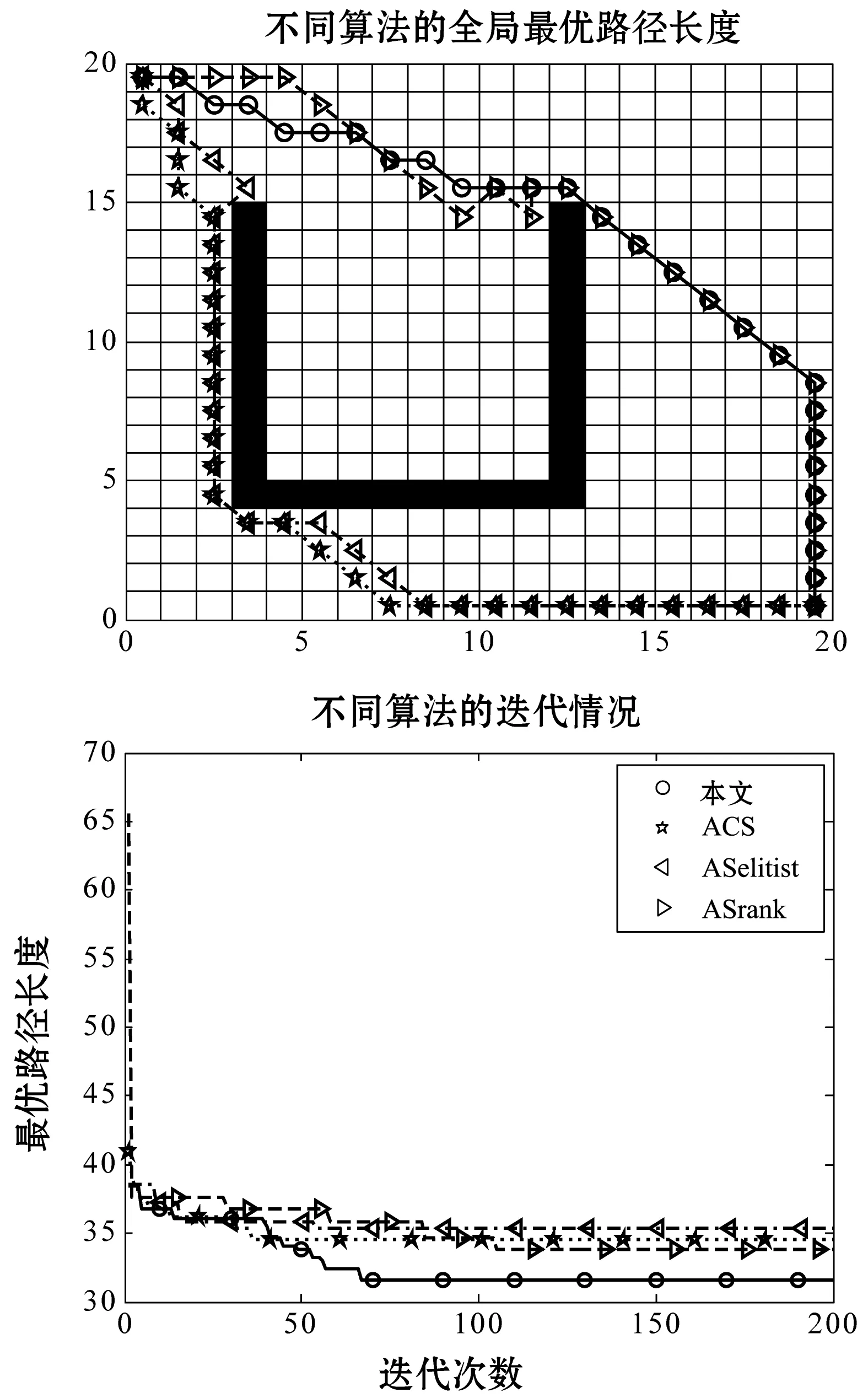
图2 U_2·左边U型障碍物路径规划和迭代情况

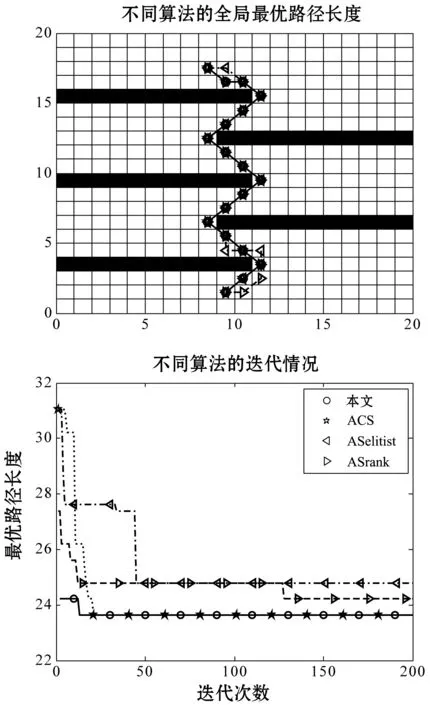
图3 Z_1·Z型障碍物简单情况的路径规划和迭代情况

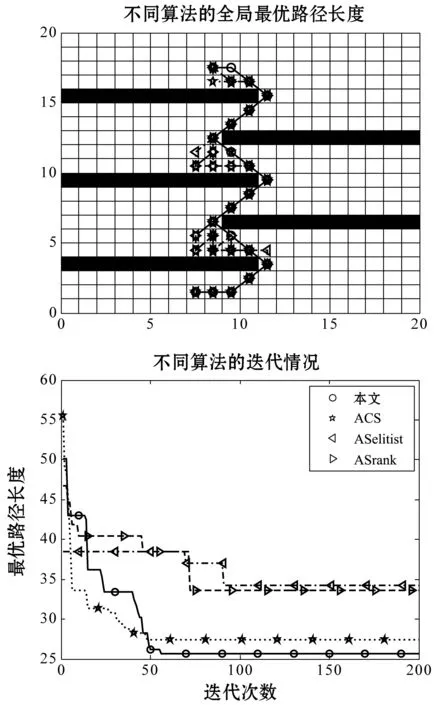
图4 Z_2·Z型障碍物复杂情况的路径规划和迭代情况

从图5得到，在这种障碍物环境下，传统算法都比较难以得到最优解，在第一个缺口处总是陷入了局部最优。可知其此处的多样性较差，因而很难寻找到全局最优。相对来讲，ACS算法比精英蚂蚁算法和排序蚂蚁算法有了很大的提高。本文算法找到了全局最优解，而对应的收敛速度只是稍微下降了一点。

图6中E型障碍物中间存在着一个缺口，相对于图5，则大大缓解了启发式构成的陷入局部最优解的威胁，所有算法都能够找到全局最优解,但本文算法是最快收敛的。

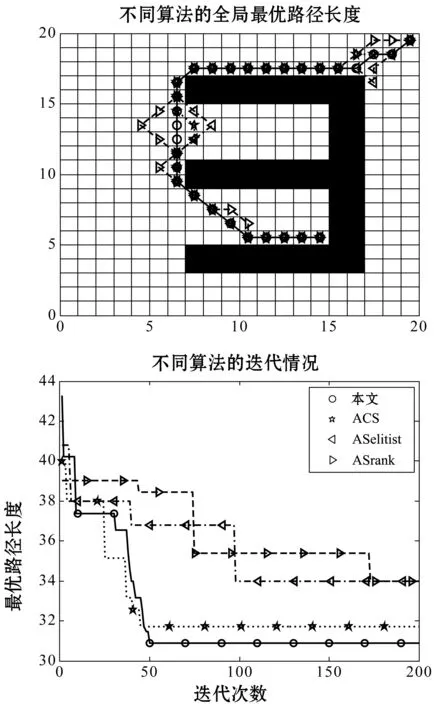
图5 E_2 无缺口的E型障碍物路径规划和迭代情况

4.2 复杂环境下四种算法的性能比较

上节给出了四种算法在简单环境下的性能比较分析，体现了本文算法的有效性。本节将验证复杂环境下算法的有效性。上节中，环境只是20乘以20的栅格，本节环境为50乘以50的栅格。解空间的增加大大增加了算法寻找最优解的难度。表2给出了复杂环境下蚁群优化算法的参数。

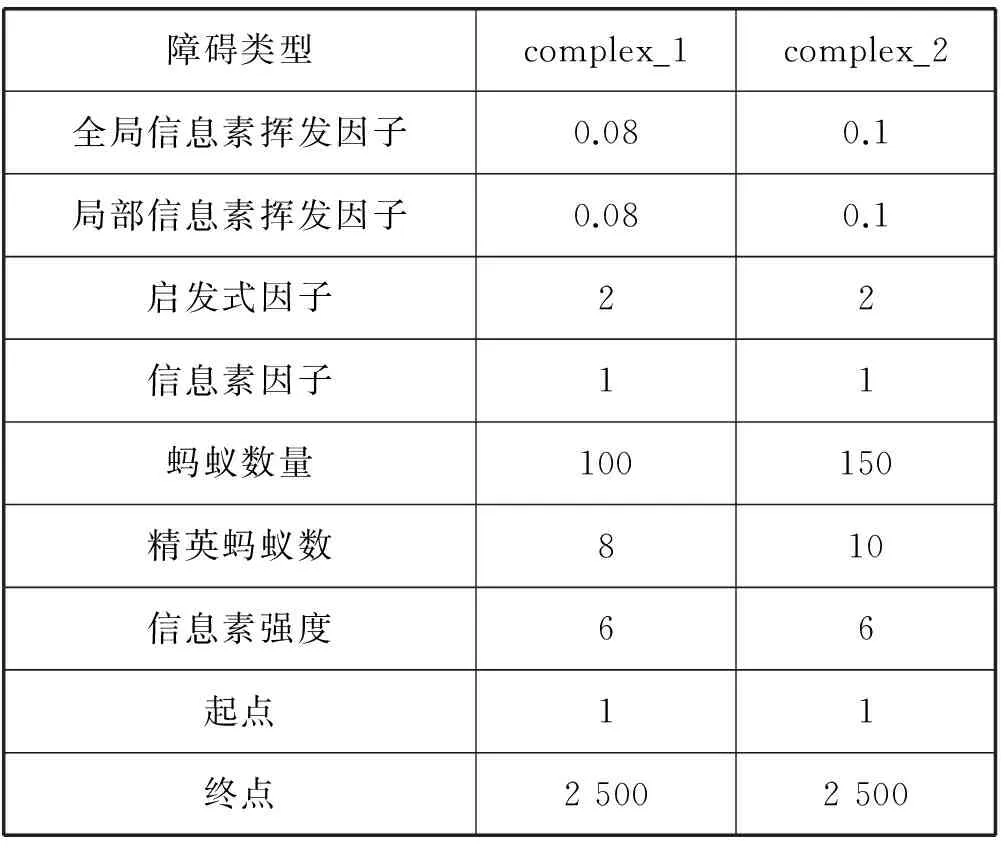
表2 复杂环境下算法的参数设置情况

图7给出了第一种复杂环境下的路径规划和迭代情况。由图可知，本文算法不仅收敛速度快，而且得到了全局最优解。而其他算法不仅收敛速度较慢，还没有得到最优解，都陷入了局部最优。

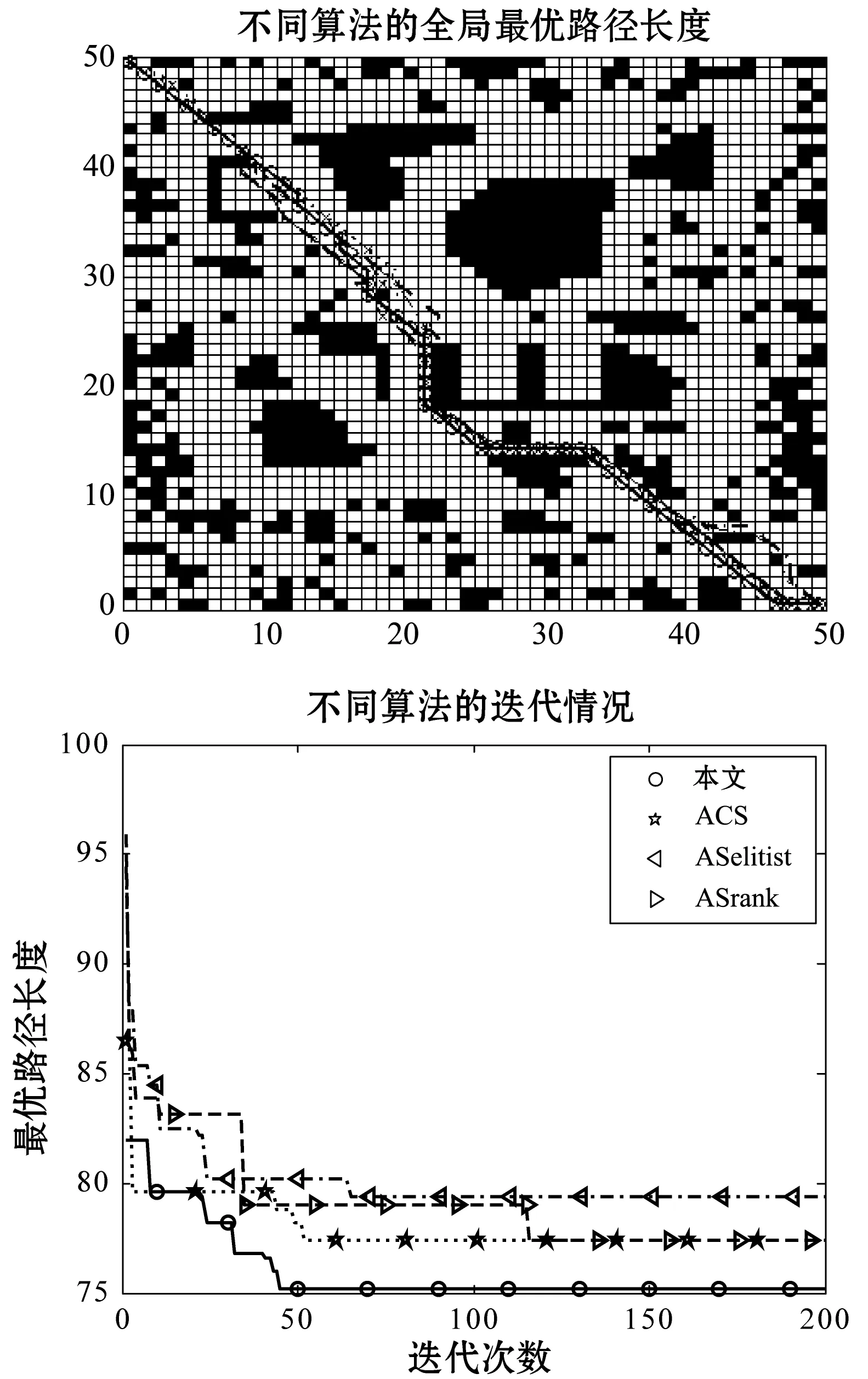
图7 complex_1·第一种复杂情况下的路径规划和迭代情况

图8是另一种复杂性的障碍地图，且比图7更容易陷入局部最优解。在这种情况下本文算法依旧得到了比较好的结果：不仅得到了最优解，而且收敛速度也是四种算法中最快的。

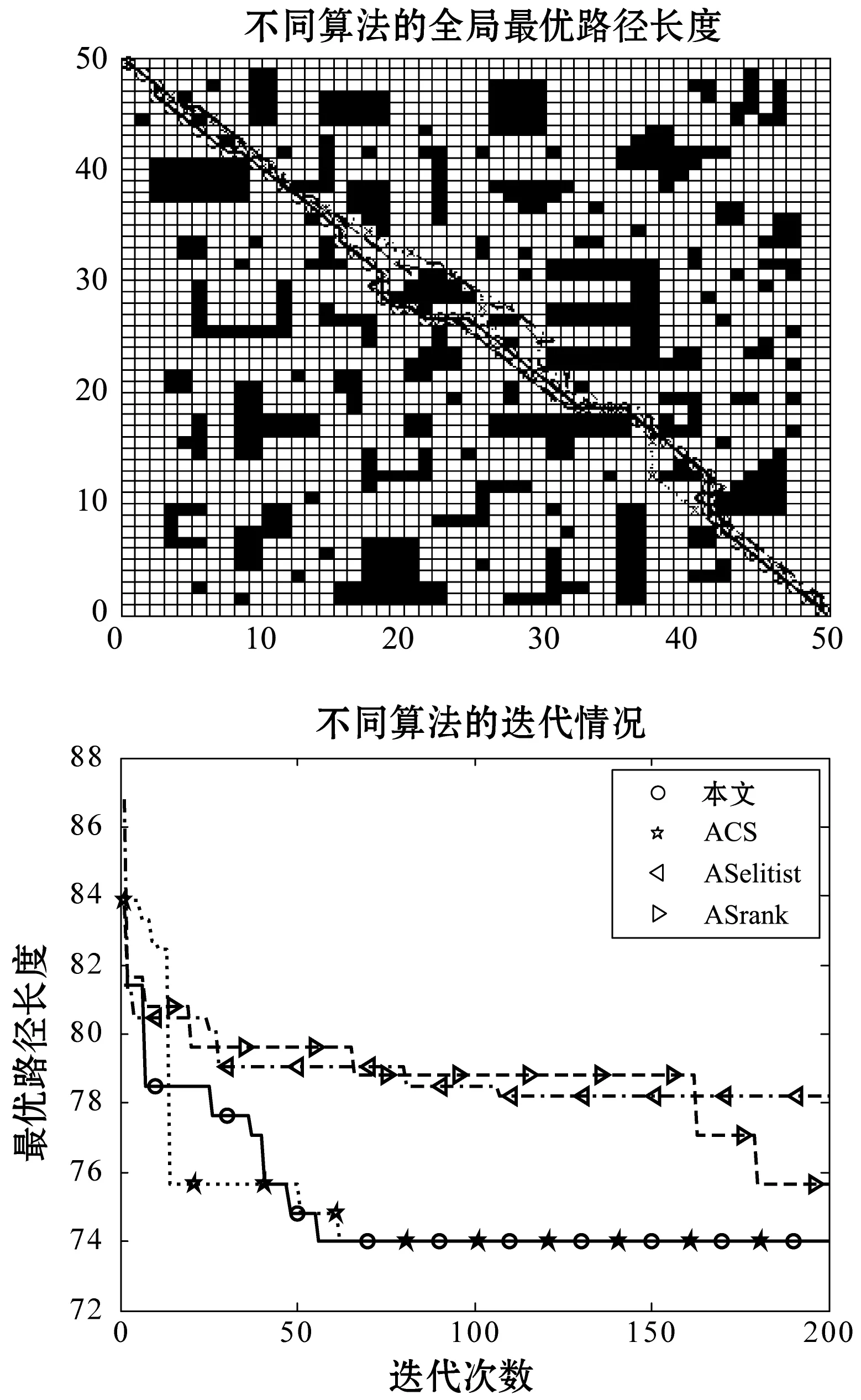
图8 complex_2·第二种复杂情况下的路径规划和迭代情况

虽然本文算法和ACS算法都能够得到最优解，并且收敛速度也只是比ACS算法稍好一点，几乎可以忽略不计。但是从迭代曲线图可以看出，本文算法在得到最优解之前能够保持一个比较稳定搜索过程，即本文算法可以在一定的平均迭代次数上，得到一个比较优良的解。比较而言，ACS算法不能保持这样的特性。另一方面，这也说明ACS可能会出现停滞行为而搜索不到最优解。此外，也说明本文算法在自适应算子下有一个比较稳定的搜索过程。

4.3 四种算法的性能分析比较

前两节分别在简单环境和复杂环境下将本文算法和经典蚁群优化算法进行了性能比较，证明了本文算法的有效性。为了进一步验证本文算法的稳定性，本节在同一种地图中(障碍如图9)，将不同算法运行20次，统计分析每种算法的结果，各个算法有着相同的参数，最大的迭代次数都为250，相关参数见表3，统计分析结果见表4所示。

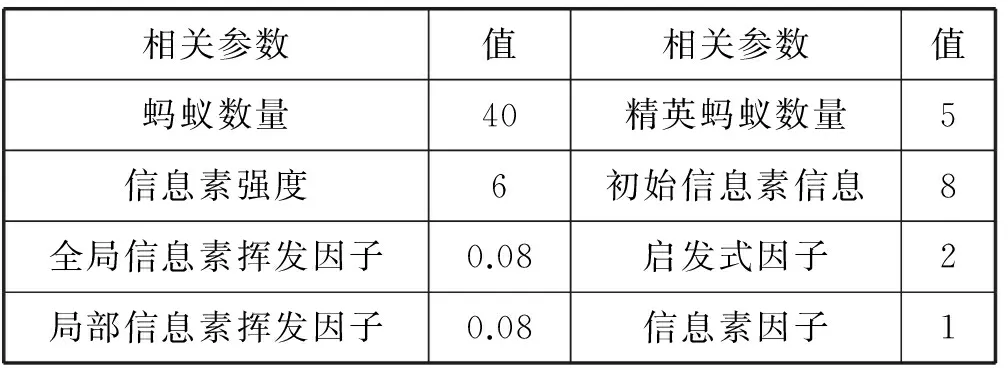
表3 算法的参数设置情况

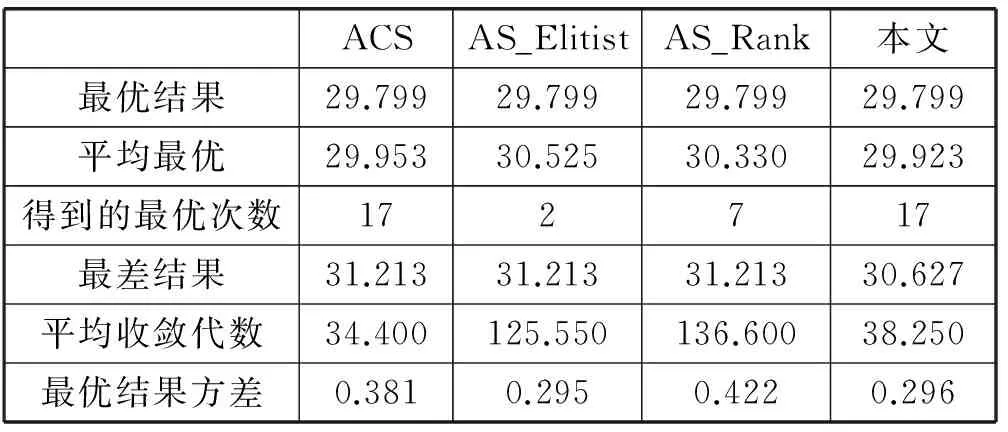
表4 不同算法的性能分析

表4分别对比了四种算法在20次情况的不同性能，最优结果，最优结果的次数，最差结果，以及算法平均的收敛速度，并分析了算法每次得到结果的方差。图9中，分别给出了本文算法和其他算法某次路径规划及相应的收敛情况。

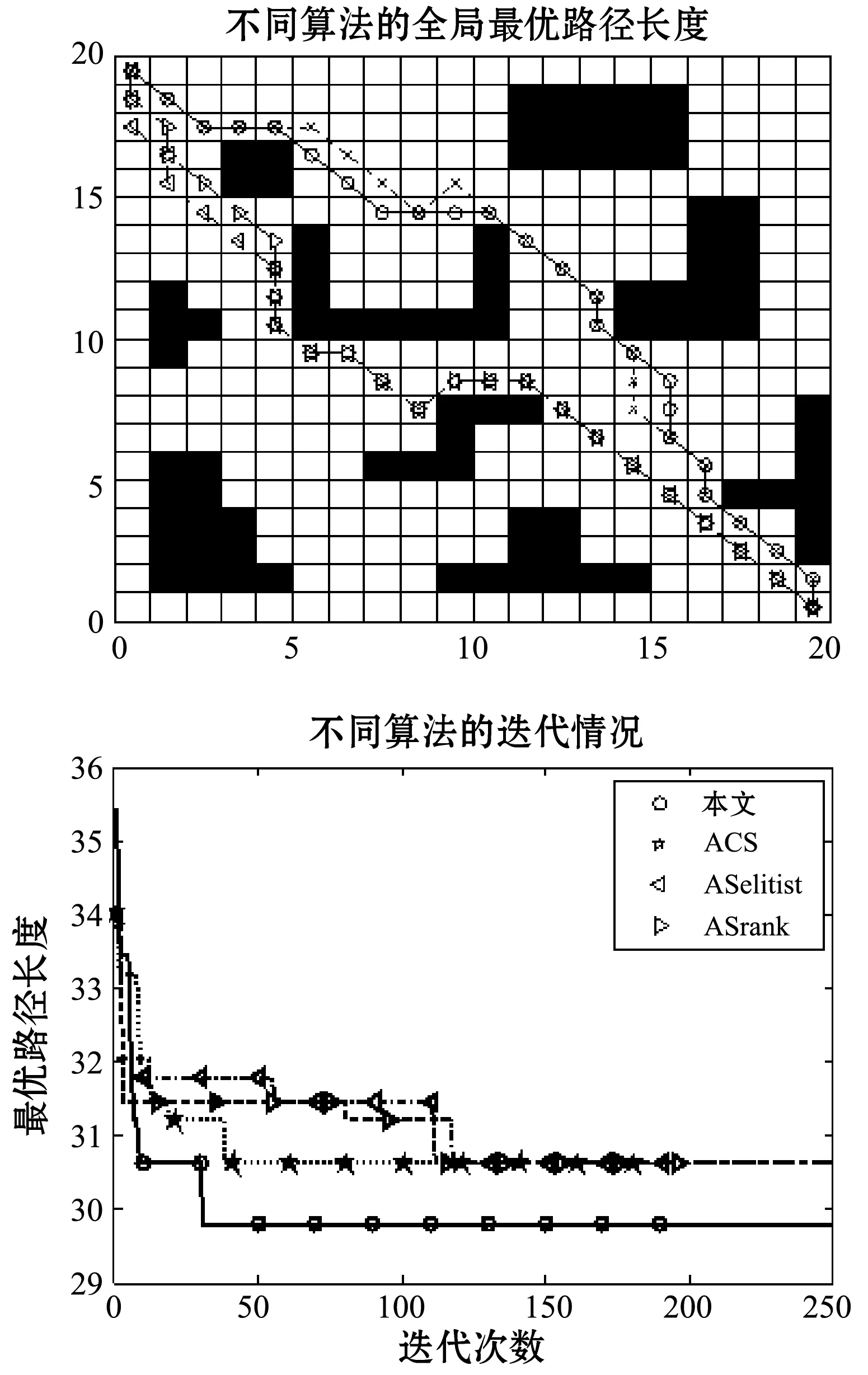
图9 不同算法的路径规划和收敛情况

由表4知，精英策略和排序策略得到的最优解的次数比较少。但精英策略比较稳定，而其最易陷入局部最优解。排序策略比精英策略的多样性要好一点，这与前面的理论分析相吻合。算法实验结果也表明这两种算法大部分都落入了如图9中的局部最优解。ACS算法得到的结果相对来说也很好，能够快速地稳定地得到最优解。本文算法的方差比ACS还低一点，表明本文算法可以更加稳定地得到解。最差结果也比ACS好，本文算法多样性更好。而本文收敛速度并没有下降很多。可知本文算法能够较快地稳定地得到最优解。

5 结 语

本文分析了蚁群算法中利用蚂蚁信息这一正反馈过程。在传统蚁群算法仅使用最优或者较优的蚂蚁信息的基础上，本文提出的基于统计分析的自适应精英蚁群算法对每一代蚂蚁的整体信息进行了统计分析，进而不仅提取了最优蚂蚁的信息，还提取了平均蚂蚁的信息以及最差蚂蚁的信息。并在信息素更新中加以运用，平衡了蚁群算法的收敛速度和跳出局部最优解间的关系。由于是对每一代蚁群的随机统计使得蚁群算法具有一定的自适应性。将算法应用于机器人的全局路径规划问题中，仿真实验结果证明了不管是在简单还是复杂环境下，本文算法都能够得到最优的解，较快的收敛速度。此外，由于本文算法可以根据每代蚁群的整体信息自适应的调整信息素的更新过程，使得本文算法维持一定范围的搜索解空间。而且，在复杂情况下，本文算法的效果更加明显。

未来，将考虑多种群蚁群算法中如何利用多个蚁群种群的相关信息，以平衡算法收敛速度和解的多样性之间的矛盾，从而解决更大规模的复杂问题，并运用在机器人的路径规划中。此外，还要讨论如何确定精英蚂蚁个数以期更加有效地解决实际问题。

[1] 徐国保,尹怡欣,周美娟.智能移动机器人技术现状及展望[J].机器人技术与应用,2007(2):29-34.

[2] 蔡自兴.中国机器人学40年[J].科技导报,2015,33(21):23-31.

[3] 朱大奇,颜明重.移动机器人路径规划技术综述[J].控制与决策,2010,25(7):961-967.

[4] Raja P, Pugazhenthi S. Optimal path planning of mobile robots: A review[J]. International Journal of Physical Sciences, 2012,7(9):1314-1320.

[5] Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 1996, 26(1): 29-41.

[6] 段海滨,王道波,朱家强,等.蚁群算法理论及应用研究的进展[J].控制与决策,2004,19(12):1321-1326.

[7] Dorigo M, Stützle T. Ant Colony Optimization: Overview and Recent Advances[J]. International, 2010, 146(5):227-263.

[8] Bullnheimer B, Hartl R F, Strauss C. A New Rank Based Version of the Ant System - A Computational Study[J]. Central European Journal of Operations Research, 1999, 7(1):25-38.

[9] Dorigo M, Birattari M, Stutzle T. Ant colony optimization[J]. IEEE computational intelligence magazine, 2006, 1(4): 28-39.

[10] 李磊,叶涛,谭民,等.移动机器人技术研究现状与未来[J].机器人,2002, 24(5)：475-480.

[11] Dorigo M, Gambardella L M. Ant colony system: a cooperative learning approach to the traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation,1997,1(1): 53-66.

[12] 吕勇.蚁群优化算法及在网络路由中的应用研究[D].杭州:浙江大学电气工程学院，2005.

[13] 杨业娟,屠莉江.基于蚁群算法的水果图像分割技术[J].江苏农业科学,2014,42(9):380-382.

[14] 张海涛,周爱武.蚁群算法在文本聚类中的应用研究[J].微电子学与计算机,2016,33(1):81-84.

[15] Farahnakian F, Ashraf A, Pahikkala T, et al. Using ant colony system to consolidate vms for green cloud computing[J]. IEEE Transactions on Services Computing, 2015,8(2):187-198.

[16] Lee S G. Multiagent elite search strategy for combinatorial optimization problems[C]// International Conference on Computer and Information Sciences. Springer-Verlag, 2005:432-441.

[17] 何琳,王科俊,李国斌,等.最优保留遗传算法及其收敛性分析[J].控制与决策,2000,15(1):63-66.

[18] 郭玉.基于改进蚁群算法的机器人路径规划研究[D].哈尔滨:哈尔滨工业大学学院控制科学与工程系，2008.

SELF-ADAPTIVE ANT COLONY ALGORITHM BASED ON STATISTICAL ANALYSIS AND ITS APPLICATION

Xu Mingle1You Xiaoming1*Liu Sheng2

1(CollegeofElectronicandElectricalEngineering,ShanghaiUniversityofEngineeringScience,Shanghai201620,China)2(CollegeofManagement,ShanghaiUniversityofEngineeringScience,Shanghai201620,China)

Path planning is one of the key technologies of robot. In this paper, the improved ant colony algorithm is applied to robot path planning. Aiming at the shortcoming of traditional ant colony algorithm which is slow to converge and easy to fall into local optimum, the dynamic random statistical analysis of each ant colony is performed based on the Ant Colony System algorithm. The optimal, average and worst ant information are extracted to form an adaptive operator for the local pheromone adaptive updating. Simulation results show that the proposed adaptive operator is effective in solving the problem of increasing the convergence speed and falling into the local optimal solution.

Path planning Adaptive elitist strategy Statistical analysis Ant colony optimization

2016-06-26。国家自然科学基金项目(61075115，61403249);上海市教委科研创新重点项目(12ZZ185)。许明乐，硕士生，主研领域：机器人应用和群智能算法。游晓明，教授。刘升，教授。

TP3

A

10.3969/j.issn.1000-386x.2017.07.038