基于平均区域划分的Laplacian稀疏编码的图像分类

史 莹 万 源 陈晓丽

(武汉理工大学理学院 湖北 武汉 430070)



基于平均区域划分的Laplacian稀疏编码的图像分类

史 莹 万 源 陈晓丽

(武汉理工大学理学院 湖北 武汉 430070)

针对稀疏编码方法中编码过程不稳定和金字塔匹配的划分方法无法使得融合后的特征很稀疏这两个问题，提出基于平均区域划分的Laplacian稀疏编码LSCARD(Laplacian sparse coding based on average region division)的图像分类方法。首先，对原始图像进行局部不变特征转化(SIFT)特征提取；然后，在稀疏编码方法中加入Laplacian正则化对局部特征进行编码，使相似的特征具有相似的码字；再利用平均区域划分以及最大值融合将编码后的特征向量进行融合；最后，采用多类SVM分类器对图像进行分类。在几个标准图像数据集上的实验结果表明，LSCARD算法具有更高的分类精度。

稀疏编码 Laplacian正则化 平均区域划分 最大值融合

0 引 言

图像分类是计算机视觉领域中一个重要的研究问题，其关键在于提取合适的特征表示图像。目前应用得最广泛的是利用局部特征，如SIFT[1]特征来表示图像。对于SIFT特征的改进，涂秋洁等[2]提出基于PCA-SIFT特征与贝叶斯决策的图像分类算法。而图像表示最原始的算法是词袋BoW(bag of words)[3]模型，为解决缺少特征点的空间关系信息的问题，Lazebnik等[4]提出利用空间金字塔匹配SPM(spatial pyramid matching)对图像进行分类。由于BoW模型中的C-means方法导致语义信息的丢失从而造成量化误差，Yang等[5]提出了基于稀疏编码的空间金字塔匹配(ScSPM)图像分类算法。该算法在图像的不同尺度上进行稀疏编码，并利用多类线性SVM分类器[6]对表示图像的特征向量进行分类。然而，ScSPM对特征的变化很敏感，因此Gao等[7]引入图Laplacian算子提出基于Laplacian的ScSPM(LScSPM或LSC)算法，改善了编码的不稳定性。另外，由于金字塔匹配的划分方法无法使融合后的特征向量很稀疏，许多学者在图像区域划分的改进和应用方面做了相关的研究。例如在图像去噪领域中，傅鹏等[8]将图像的平均区域划分ARD(average region division)方法应用在噪声估计中，提出一种遥感图像信噪比评估和度量准则。Liu等[9]提出对于盲目去噪的单图像噪声水平估计。由于稀疏表示理论为图像去噪方法带来了新思路，将其与冗余字典结合，周确[10]提出基于区域划分和字典学习的图像去噪方法。在图像检索方面，张旭等[11]利用一种结合SIFT和Harris特性的尺度空间兴趣点检测(IPDSH)和空间区域划分的方法对图像进行检索，有效提高了图像的检索准确率。另外，对于合成孔径雷达(SAR)图像，张光胜等[12]将图像划分成尺寸变化的子图像块，并与马尔可夫随机场模型(MRF)结合，对SAR图像实现变化检测。Kazuhiro等[13]利用图像特征的空间域和频域，并将图像划分成单独的几个图像块，从而改善图像的检索效率。对于图像分类的应用，唐峰等[14]提出基于改进稀疏编码模型的图像分类算法，利用ARD方法和随机森林多分类器，提高了图像分类的性能。姜宇恒[15]提出基于区域划分的极化SAR图像分类算法研究，并取得了较好的分类效果。

上述的研究中，遇到的第一个问题就是稀疏编码SC(sparse coding)在编码过程中极其不稳定，相似特征之间的多种组合方式会导致相似的特征可能会被编成不同的码字。而第二个问题是图像区域划分中金字塔匹配方法运用使得融合后的特征无法很稀疏。因此，为了解决第一个问题，由于Laplacian正则化可以提取图像的空间几何信息来保持相似特征之间编码的一致性，从而改善编码的不稳定性，因此本文首先在SC的优化问题中引入Laplacian正则化。针对第二个问题，从上述的研究成果中可以看出，图像的ARD凭借其操作简单、快速等优点应用得最广泛。因此，本文将LSC方法结合图像的ARD，提出一种基于ARD的Laplacian稀疏编码的图像分类算法，即LSCARD。该方法利用Laplacian正则化提取更多的图像空间几何信息并保持特征空间中特征的依赖关系和相似信息，而图像的ARD使得区域融合后的特征向量尽可能稀疏并具备空间信息，因此可得到较低的重构误差和较好的分类性能。

1 相关工作

对于图像分类来说，局部特征的适当编码不仅可以简洁准确地模拟图像，而且还可以提高图像分类的效率。因此，在这节中将回顾两种典型的编码方法：向量量化和稀疏编码。

相关符号说明：X=[x1,x2,…,xn]∈Rd×n为输入的SIFT特征矩阵，A=[a1,a2,…,ak]∈Rd×k代表字典(或码本)，S=[s1,s2,…,sn]∈Rk×n为相应的编码。

1.1 向量量化

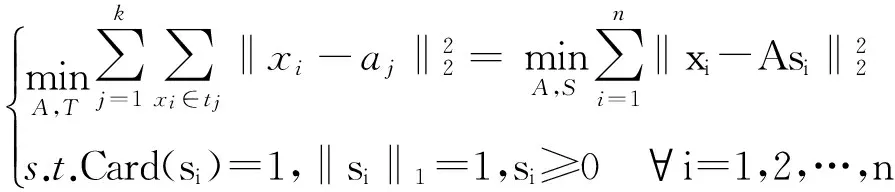
(1)

其中，S∈Rk×n为聚类指标矩阵即X的编码集；‖·‖2和‖·‖1分别代表l2-范数和l1-范数；Card(si)=1代表si的仅一个元素非零；si≥0表示向量si的所有元素非负；所有这些约束条件加起来表示向量si中有且仅有一个元素的值为1。

对于式(1)的简单解法是对于每一个局部特征xi搜索其最近邻，并给相应的指标标记为1，其他的标记为0。

1.2 稀疏编码(SC)

由于VQ方法很容易导致量化误差，并且C-means方法可能会使语义信息丢失，因此Yang等[5]提出了基于SPM的稀疏编码方法(ScSPM)即SC。其核心问题是学习k空间中的超完备(即k≫d，基向量的个数远大于维数)字典A，并选取其中尽可能少的基向量来表示原始的特征向量。该方法利用空间金字塔划分方法进行稀疏编码，它首先训练用于稀疏编码的基向量，再利用得到的基向量和对图像进行空间划分方法，将不同金字塔层次得到的向量直接相连构成一个向量，从而利用此向量表示图像的特征。因此，图像中的每个特征都是由字典中的多个基向量表示，减少特征点的量化误差，从而能更准确地描述一幅图像的特点。具体优化问题如下：

(2)

其中，S∈Rk×n为相应的稀疏编码；λ为正则化参数，用来平衡重构误差和编码的稀疏性；aj为矩阵A的第j个列向量。

对于式(2)的通常解法是交替固定A(或S)从而优化S(或A)，直到目标函数的值达到指定的极值即可。首先固定X和A，则优化问题可以转化为通过优化每一个编码系数si来解决。即：

(3)

针对式(3)，可以通过特征符号搜索算法[16]来求解。固定X和S，则相应地将优化问题转化为二次约束的最小平方问题。即：

(4)

利用共轭梯度法或Lagrange对偶方法[16]可得出式(4)的解。

2 基于平均区域划分的Laplacian稀疏编码

虽然传统的LSC方法能提取图像的空间几何信息，保留相似特征编码的一致性和稳定性，但该方法在划分图像时利用的是金字塔匹配，由于金字塔的第一层和第二层划分的局域数量较小，使得融合后的向量无法达到很稀疏，并且缺乏空间信息。而ARD是将一幅图像平均划分为大小相等的方块，利用最大值融合方法能使融合后的每一个图像的特征向量都尽可能达到稀疏并保留空间信息，因此本文结合ARD和最大值融合提出LSCARD的图像分类方法。LSCARD方法的整体框架如图1所示。

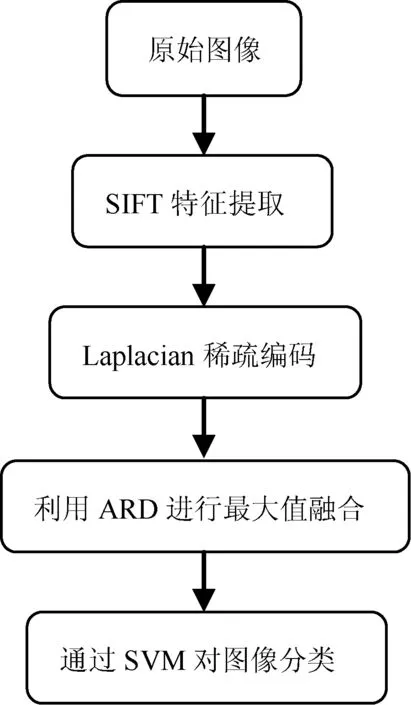
图1 LSCARD算法的整体框架

2.1 Laplacian稀疏编码

Laplacian稀疏编码方法最初是由Gao等[7]考虑到传统的SC方法对特征变化很敏感，且相似的局部特征之间缺乏判别能力，因此引入Laplacian矩阵保留特征之间编码的一致性，使得编码过程不再独立。相应的优化问题如下：

(5)

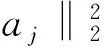
(6)

其中，k是两个直方图的维数(即字典的尺寸)，Him和Hjm分别表示特征xi和xj落入直方图Hi和Hj的数量，即向量Hi和Hj的第m个元素。

对于式(5)来说，同时求解A和S是非凸的，但是固定A(或S)求S(或A)却是凸的。一般的解法是：首先从所有局部特征中随机选择部分局部特征即模板特征来训练A和S。在交替更新A和S的过程中，分别采用共轭梯度法和特征符号搜索算法[16]。当有新的特征出现时，就可以得到对于新特征的稀疏编码。

下面具体介绍利用特征符号搜索算法求编码的步骤。首先固定特征X和字典A，优化S。为了优化S，我们逐个优化si，固定所有剩下的sj(j≠i)。相应的优化问题如下：

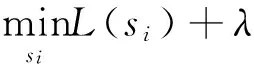
(7)

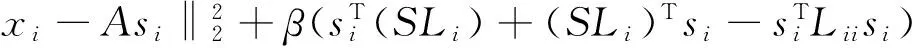
接下来，利用算法1求解式(7)。算法中涉及的公式定义如下：

(8)

(9)

其中，矩阵S-i是去掉矩阵S的第i列的子矩阵，向量Li,-i是去掉Li第i项的子向量，E是单位矩阵。

算法具体步骤如下：

算法1 特征符号搜索算法求稀疏编码

输入：字典A，特征矩阵X的第i个特征，初始化编码S，参数λ和β以及Laplacian矩阵L

输出：第i个特征的稀疏编码si

step 1 初始化si=0，θ=0，其中，θi∈{-1,0,1}表示系数的符号，activeset:={}。

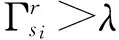
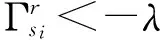
其中，θm是θ的第m个分量。

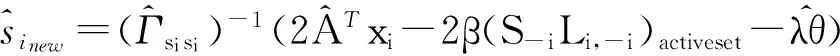
(10)

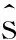
step5 检查最优化条件：

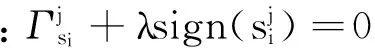
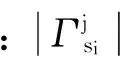
2.2 利用ARD进行最大值融合

这节将介绍利用ARD对图像进行划分，由于ARD是对给定图像平均划分为多个区域，因此结合最大值融合方法可使融合后的特征向量尽可能稀疏，有效地克服了金字塔的不同尺度所划分的局域数量较小并无法顺畅地传递空间信息的缺点。在对图像进行SIFT提取阶段，若每个SIFT描述子是在p×p的像素块上计算所得，则将每幅图像I平均分成p(p=q×q)个方块。因此，在对图像进行LSC之后，可以利用ARD将这些稀疏特征进行最大值融合，从而得到图像的最终表示。具体步骤如下：

输入：图像I，图像划分的区域数量p=q×q，字典A

输出：融合后的特征向量z∈Rp×k，其中k为字典的个数

step 1 将图像I平均地划分成p个方块，并提取每一个方块中的SIFT特征。

step 2 利用算法1求解特征的稀疏编码系数，得到每一个SIFT特征向量X∈R128×n的稀疏编码S∈Rk×n。

step 3 采用最大值融合方法将每一个方块中的所有稀疏编码利用ARD进行融合，即：

vl=max{|s1l|,|s2l|,…,|snl|},l=1,2,…,k

(11)

其中，snl是稀疏编码sn的第l个元素；而vl是向量v的第1个元素。而每一方块的稀疏向量可用v=[v1,v2,…,vk]表示。

step 4 将表示该图像中每一方块的稀疏向量v按照这个方块所在位置拼接成表示该幅图像的稀疏向量z，即：z=[v11,…,v1k,…,vi1,…,vij,…,vik,…,vp1,…,vpk]

(12)

其中，vij是表示第i个方块的稀疏特征向量的第j个元素。

得到图像的最终表示之后，对于图像分类，由于线性SVM具备快速、低复杂度等优点，因此，本文采用多类线性SVM分类器。

3 实验仿真

为了验证本文LSCARD算法的有效性，分别在Corel-10[18]、Scene-15[19]和Caltech-101[20]三个标准数据集上进行仿真实验。并将其与三种稀疏编码方法的分类准确率进行比较。

3.1 图像数据集

这节将介绍三个标准的图像数据集，包括Corel-10、Scene-15和Caltech-101数据集。具体如表1所示。其中，Scene-15数据集的部分图片如图2所示。

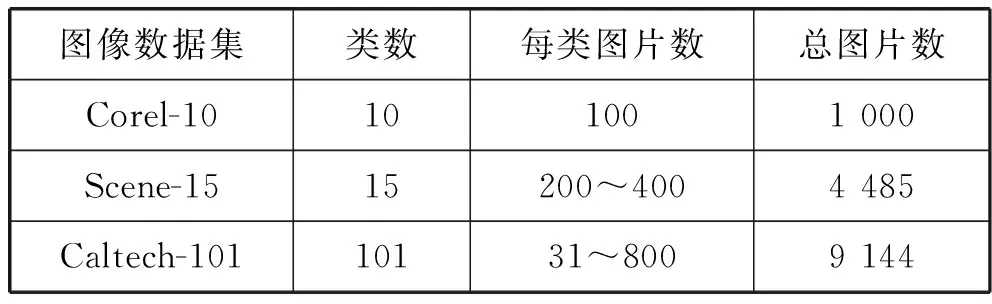
表1 三个标准图像数据集(张)

图2 Scene-15数据集中部分图片

3.2 实验设置

对于ARD中的空间划分粒度，本文选取4×4的粒度。在特征提取阶段，利用16×16的窗口，步长为8提取图像的SIFT特征。对于训练字典的过程，固定字典的尺寸为k=1 024。使用K最近邻构建相似W矩阵时，K=5。

针对LSC优化问题中的目标函数，有两个重要的参数λ和β。本文依照文献[7]中的方法，对于不同的图像数据集设置不同的值。例如，对于Corel-10和Scene-15数据集，λ=0.4,β=0.2；对于Caltech-101数据集，λ=0.3,β=0.1。

3.3 实验步骤

首先，对于上述的三个标准图像数据集，将每一个数据集随机分成10份，并利用10-折交叉验证来证明本文方法的有效性。然后，记录基于10-折交叉验证的LSCARD方法的平均分类准确率和标准差。最后，将本文方法与其他三种稀疏编码方法进行比较并分析相应的实验结果。

3.4 实验结果与分析

表2、3、4给出了LSCARD方法与一些知名的稀疏编码方法包括ScSPM、LScSPM和SC-RF[14]在上述三个标准图像数据集上的分类效果比较。

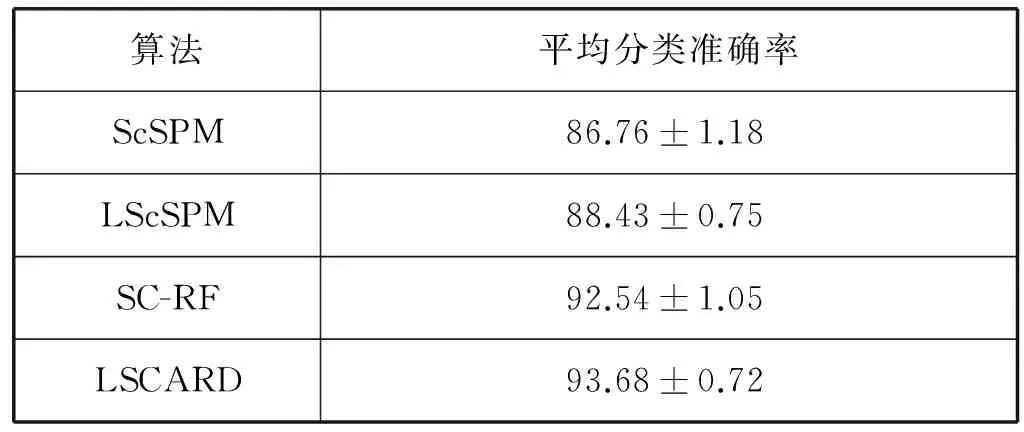
表2 Corel-10数据集上的分类结果 %

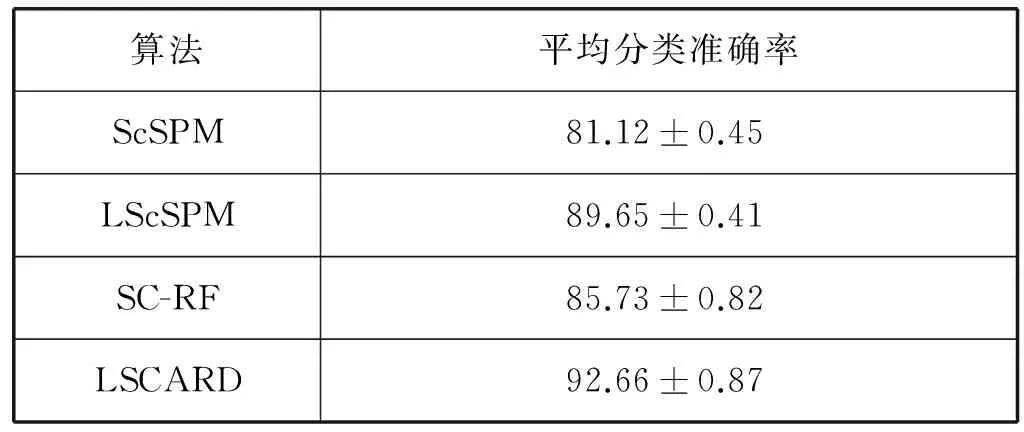
表3 Scene-15数据集上的分类结果 %

从上述这三个表可以看到，LSCARD方法在所有图像数据集上的平均分类准确率都比其它三种编码方法要高。具体地，对于ScSPM和LScSPM这两种方法，由于其在进行图像划分时，利用的是金字塔匹配，这会造成金字塔的第一层和第二层因划分的局域数量较小，使得融合后的特征无法很稀疏，并且缺乏空间信息。而LSCARD方法利用的是将图像平均划分为多个区域，这不仅使得融合后的特征尽可能稀疏，而且还具备空间信息，因此更能准确地表示图像。对于SC-RF来说，由于其缺乏Laplacian正则化的使用，因此相似的编码可能被编成不同的码字。而LSCARD方法利用Laplacian算子能提取更多的空间几何信息，保持编码的一致性并使编码过程不再独立。因此，从整体上看，本文的LSCARD方法能显著地提高图像分类准确率。

3.5 复杂度分析

给定一幅图像的局部特征数量为n，模板特征的数量为n1，字典的数量为k，则总的局部特征和模板特征之间相似度的计算的复杂度为O(n×n1)，特征符号搜索算法[16]的复杂度为O(n×k)，因此编码阶段的总复杂度为O(n×n1+n×k)=O(n×(n1+k))。针对编码融合阶段，空间金字塔划分过程中涉及到金字塔的层数pLevels和直方图的个数nBins，因此复杂度为O(2×n+pLevels×nBins)。而本文方法在融合阶段利用的是平均区域划分，假设一幅图像的区域划分数量为p，则该阶段的复杂度为O(p×k)。因此，LSCARD方法的总复杂度为O(n×(n1×k)+p×k)，远小于利用空间金字塔划分进行特征融合的算法的复杂度。

4 结 语

针对SC方法中不稳定和金字塔匹配的划分方法无法使得融合后的特征很稀疏这两个问题，本文提出LSCARD的图像分类方法。由于Laplacian正则化能降低由字典的超完备性造成稀疏编码对局部特征的敏感性，并保留了相似特征编码的一致性，使得对局部特征的表达更具鲁棒性。同时由于使用ARD对图像进行划分，结合最大值融合，能使融合后的特征更稀疏并带有空间信息。因此，在图像表示阶段，通过利用特征之间的依赖性和稀疏性可以更准确地模拟图像。在三个标准图像数据集上的实验结果也表明本文的LSCARD方法与已有的三种编码算法相比有更好的性能。

[1] Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004,60(2):91-110.

[2] 涂秋洁, 王晅. 基于PCA-SIFT特征与贝叶斯决策的图像分类算法[J]. 计算机应用与软件, 2016,33(6):215-219.

[3] Sivic J, Zisserman A. Video Google: A text retrieval approach to object matching in videos[C]//Proceedings of the International Conference on Computer Vision,2003,2:1470-1477.

[4] Lazebni S, Schmid C, Ponce J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2006,2:2169-2178.

[5] Yang J C, Yu K, Gong Y H, et al. Linear spatial pyramid matching using sparse coding for image classification[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2009:1794-1801.

[6] 杨淑莹. 模式识别与智能计算—Matlab技术实现[M].2版.北京: 电子工业出版社, 2011:126-133.

[7] Gao S H, Tsang I W, Chia L-T, et al. Local features are not lonely-Laplacian sparse coding for image classification[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2010:3555-3561.

[8] 傅鹏, 孙权森, 纪则轩, 等. 一种遥感图像信噪比评估和度量准则[J]. 测绘学报, 2013,42(4):559-567.

[9] Liu X H, Tanaka M, Okutomi M. Single-image noise level estimation for blind denoising[J].IEEE Transcations on Image Processing, 2013,22(12):5226-5237.

[10] 周确. 基于区域划分和字典学习的图像去噪方法[D]. 西安: 西安电子科技大学, 2013.

[11] 张旭, 郭宝龙, 孟繁节, 等. 基于IPDSH兴趣点空间区域划分的图像检索[J].吉林大学学报(工学版),2013,43(5):1408-1414.

[12] 张光胜, 李长春, 邹友峰. 基于自适应分块马尔可夫随机场(MRF)模型的SAR图像变化检测研究[J].科学技术与工程,2014,14(16):6-10.

[13] Kazuhiro K, Chen Q. Image retrieval using features in spatial and frequency domains based on block-division[C]//2015 International Conference on Computational Science and Computational Intelligence,2015:448-453.

[14] 唐峰, 孙锬锋, 蒋兴浩, 等. 基于改进稀疏编码模型的图像分类算法[J].上海交通大学学报,2012,46(9):1406-1410.

[15] 姜宇恒. 基于区域划分的极化SAR图像分类方法研究[D]. 西安: 西安电子科技大学, 2014.

[16] Lee H, Battle A, Raina R, et al. Efficient sparse coding algorithms[C]//Advances in Neural Information Processing Systems,2006:801-808.

[17] Wu J X, Rehg J M. Beyond the Euclidean distance: Creating effective visual codebooks using the histogram intersection kernel[C]//Proceedings of IEEE 12th International Conference on Computer Vision, 2009:630-637.

[18] Lu Z W, Ip H H S. Image categorization with spatial mismatch kernels[C]//IEEE Conference on Computer Vision and Pattern Recognition, 2009:397-404.

[19] Li F F, Perona P. A Bayesian hierarchical model for learning natural scene categories[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005,2:524-531.

[20] Li F F, Fergus R, Perona P. Learning generative visual models from few training examples: An incremental Bayesian approach tested on 101 object categories[J].Computer Vision and Image Understanding,2007,106(1):59-70.

IMAGE CLASSIFICATION BASED ON AVERAGE REGION PARTITIONING AND LAPLACIAN SPARSE CODING

Shi Ying Wan Yuan Chen Xiaoli

(SchoolofScience,WuhanUniversityofTechnology,Wuhan430070,Hubei,China)

For the sparse coding method, the coding process is unstable and the pyramid matching method can not make the fusion feature very sparse, an image classification method based on Laplacian sparse coding with average region partition is proposed. Firstly, local invariant feature transform (SIFT) feature extraction was applied to the original image. Then, Laplacian regularization was added to the sparse coding method to encode the local features so that the similar features have similar code words and the feature vectors were fused by average region partition and max pooling. Finally, multi-class SVM classifier was used to classify the images. Experimental results on several standard image datasets show that the algorithm has higher classification accuracy.

Sparse coding Laplacian regularization Average region division Maximum fusion

2016-07-14。国家自然科学基金项目(81271513,91324201)。史莹，硕士生，主研领域：图像处理与模式识别。万源，副教授。陈晓丽，硕士生。

TP391.4

A

10.3969/j.issn.1000-386x.2017.07.027