云计算中最小化任务完工时间的多资源调度算法

杨 鹏 靳 丹 张 晟 徐 鑫 姚建国

1(国网甘肃省电力公司信息通信公司 甘肃 兰州 730050)2(上海交通大学 上海 200240)



云计算中最小化任务完工时间的多资源调度算法

杨 鹏1靳 丹1张 晟2徐 鑫2姚建国2

1(国网甘肃省电力公司信息通信公司 甘肃 兰州 730050)2(上海交通大学 上海 200240)

云计算中Hadoop平台上默认调度方式FIFO是以公平性为目标，然而考虑单一因素会使资源利用率低下以及任务完成时间过长。在公平性和完成时间的权衡中，运行时间指标更为重要。据此，建立云计算下多资源和应用程序任务以及调度的数学模型和其目标函数，运用归约方法和具有强大计算能力的工具MINI SAT SOLVER去求解问题。仿真实验结果表明，在不同的资源供给条件下，基于MINI SAT SOLVER的次优算法比YARN(Yet Another Resource Negotiator)中默认的调度算法FIFO缩短了任务的完工时间，优化比率最高可以达到30%。

云计算 调度算法 NP完全问题 完工时间

0 引 言

云计算是基于互联网的一种新型服务模式，用户通过支付一定的金额，便可获取到高性能、高保障性、高扩展性的服务资源。这种资源主要包括软件服务资源、平台服务资源、基础设施服务资源等。由于云计算具有易用性，随时部署，相对于传统经济所提供的服务更为可靠的这些特征，越来越多的企业和个人选择将工作流放在云端执行，通过云进行大量的科学计算以及存储[1]。随着云服务处理数据量的攀升以及用户对于云服务质量的提升，云服务提供商的计算机资源变得相对欠缺，经发现，传统云服务中资源利用率比较低，可以通过提高云服务中的资源调度效率的方式，缓解或解决云服务中计算机资源稀缺的问题。

当前的云计算多租户多资源调度算法中存在许多问题。面对不同租户所要求的服务质量不一致，和不同工作流对于计算资源需求的不一致，传统的一些调度算法难以针对性地完成调度任务。当前，工业界着手探索Hadoop平台上所推出的基于多资源的管理框架——YARN，提出以资源集合——容器为粒度的调度，提高多资源利用率和相关评价指标[2]。

在YARN中，默认采用先进先出FIFO的调度算法，是按照先进先出的优先队列原则选择执行的任务[3]。然而，这种调度算法只考虑到了公平性这样的单一因素，会使资源利用率低，并且极大地增加了任务的完工时间。本文认为，在公平性和完成时间的权衡中，运行时间指标更为重要。据此，本文采用具有强大计算能力的工具和归约方法，研究了在云平台多资源调度框架下的完工时间优化问题和解决方法。

1 云计算多资源问题的数学建模

1.1 云计算资源的建模以及任务模型的建模

我们定义一个云平台拥有n台服务器，其中某个节点拥有的资源可以表达成一组向量：

rw=〈k1,k2,…,km〉w≤n

(1)

其中m为总资源的分类,ki(1≤i≤m)表示第m资源的总资源量，r表示云平台所有服务器资源的集合。

定义每个application可以表达成一个如下的向量：

va=〈pa,sa〉

(2)

其中p是一个正整数，表达了这个application的优先级，越大表示其优先级越高，下标a表示属于的那个application编号。

sa定义了编号为a的应用的任务集合taskSet，所有application的task集合表示为{task}，简写为s，每个task可以表达成：

(3)

taskSet中的task有严格的先后关系，定义在taskSet中的全序关系Before表示成：

(4)

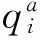
1.2 云计算调度算法相关建模

定义task执行序映射集合：

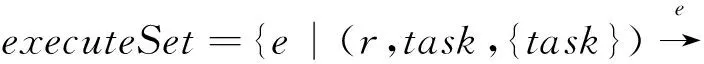
(t,n)∀task,t∈N}

(5)

定义task是否处于running状态的函数为：

(6)

定义task在时间t是否完成：

(7)

定义调度函数集合:

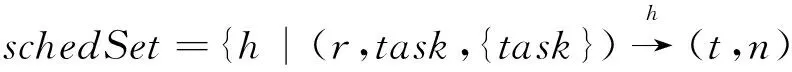
task,t∈N}

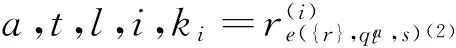
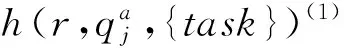
(8)

1.3 目标函数的定义

我们定义指标效率为一个调度算法在时间t的效率：

(9)

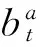
(10)

定义指标资源利用率为一个调度算法在时间t的资源利用率：

(11)

定义指标公平性为各个任务的进度方差：

(12)

定义一个调度算法的工作时长：

makeSpan(h,r,{task})=min(t)

s.t.∧taskisDone(h,r,task,{task},t)=true∀task

(13)

1.4 调度算法在目标函数下的性质

我们定义对于指标A(不包括工作时长)在时间t下的最优调度函数为：

(14)

不同的优化指标有一定联系，但同时具有一定的独立性。事实上，不可能存在一种调度算法使得它同时是指标效率最优且是指标资源利用率最优，考虑反证法：

假设存在算法，如果它是指标资源率最优，取0时刻，这时寻找往后第一个不属于其应用，只有一个任务且资源需求小于等于此时调度任务的任务，并调高对应所属应用的优先级使其大于当前调用应用程序的优先级，称此调度算法为S1。显然有在时刻0，算法S在资源利用率上优于算法S1的，算法S1在效率上优于算法S的。

这说明了不存在一种调度算法在任何情况下都是最优的，即不同的算法设计应该对应不同的目标函数。

下面，我们将考虑云计算多资源调度问题在不同的目标函数下的复杂度。

证明在指标效率下的调度问题的复杂度为NPC，即判断时间t，指标效率能否大于等于e，此算法的复杂度为NPC。

先证明，它属于NP问题，首先给定e所生成的ta,l，显然验证e是否属于schedSet只要多项式时间(O(a×1×T)，我们认为t有最大上限T)，计算指标效率也只需要多项式时间，总体需要多项式时间。

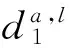
证明在指标资源利用率下的调度问题的复杂度为NPC，即是判断时间t，指标效率资源利用率大于等于M，此算法的复杂度为NPC。

NP证明与在指标效率下的证明类似，故略去。

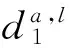
事实上，取特定的时刻，云计算中多资源调度问题属于多维多背包问题。考虑时间因素，不考虑背包容量时，云计算中多资源多调度问题属于排序调度变种问题。两者都是NP完全问题，且没有fptas近似算法。

2 基于MINI SAT SOLVER的次优算法

2.1 MINI SAT SOLVER

作为NPC问题的始祖，SAT问题一直是算法研究当中的重点。近几年来，对于SAT问题研究的一个重大突破，即是高效的SAT SOLVER的诞生。SAT SOLVER结合了高效的回溯算法，如DPLL(Davis-Putnam-Logemann-Loveland)这种算法经过40年的验证依然证明了其高效性，被广泛运用于一阶逻辑以及自动证明的基础[4]。还有一些启发式原理，如选择满足子式最多的赋值，选择短子式并对其进行赋值等。

实践上，SAT SOLVER在解决几百万子式数量级的问题时依然有不俗的性能表现，几乎能在1秒内得出结果[6]。基于此，我们假设，如果有一个问题能有效地转化为SAT问题，那么它的性能会有相对的保证。本文将在后文实验中，会试图对SAT SOLVER做一些性能测试来验证其可接受输入规模的范围。

MINI SAT SOLVER作为SAT SOLVER的一种，具有开源，易于修改，轻巧等特点，它曾获得三界工业界的奖杯，也获得过2005年SAT COMPETTION的嘉奖。由于SAT SOLVER的高效性、准确性，本文决定采用MINI SAT SOLVER作为处理问题的工具方法。

2.2 典型问题描述

相比于YARN中默认的调度算法所考虑的公平性因素，我们认为最短工作时长指标更为重要，无论是以任务吞吐率，还是以资源利用率来说，都和它们有着千丝万缕的联系。最短工作时长的典型问题，面对同一任务集合，每个任务独立需要占有相应的资源(App1先后需要单位时间的CPU，两单位时间的Network和单位时间的IO资源，App2需要单位时间的Network，IO资源和CPU资源，App3需要单位时间的CPU，单位时间的IO和单位时间的Network资源)，那么存在两种可行的调度方式，如表1和表2所示。但是其最大的不同是时间，显然在指标工作时长最优的情况下，应该选择总时长最短的调度方式，也就是第一种。我们要完成的算法，应要正确地得出时长最短的调度策略。

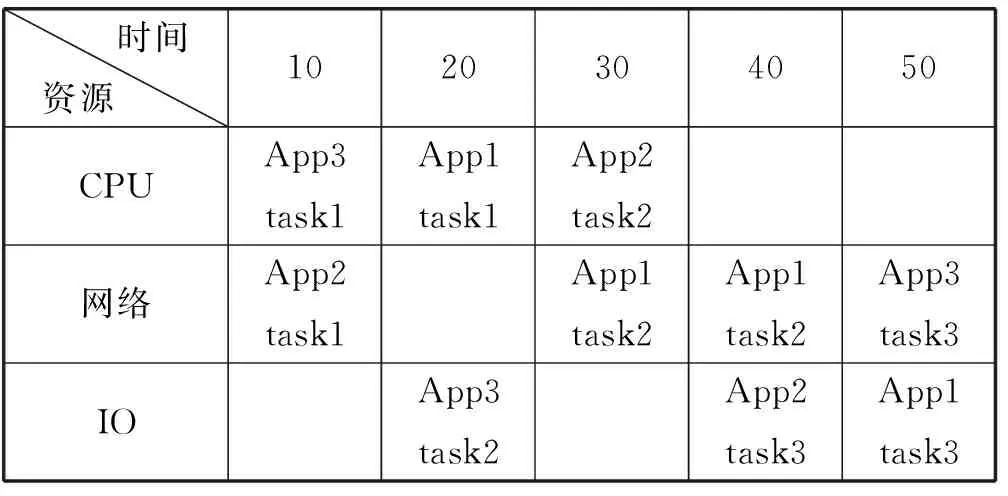
表1 同一任务集的第一种调度方法

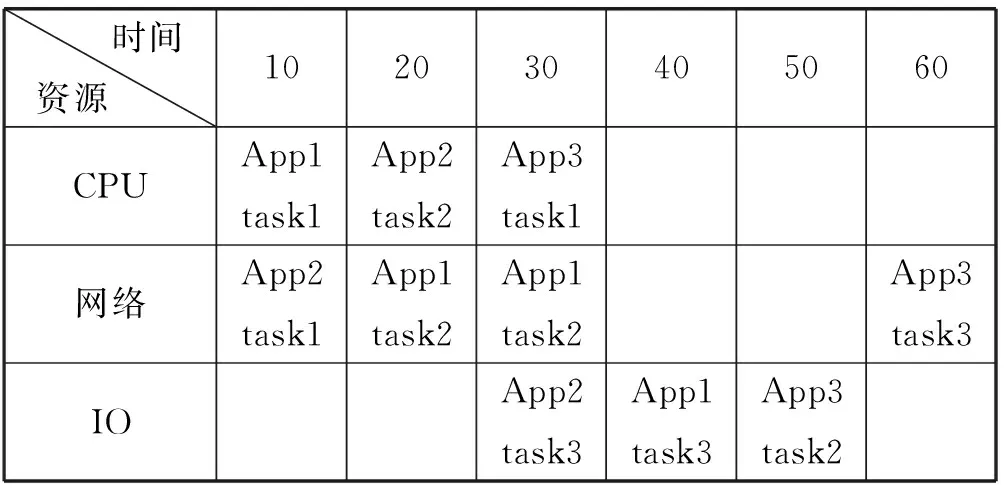
表2 同一任务集的第二种调度方法

2.3 次优算法的描述

本文运用SAT SOLVER解决以最短时长为目标函数的云计算多资源环境下的调度问题可以分成两个步骤，一是分配，二是约束。

分配步骤的原因是在于：为了适配于MINI SAT SOLVER，我们需要把同种资源但具有不同资源量的资源分解成不可分割的最小单位资源。但由于同种资源具有同质性，需要多个单位资源的任务的分配可能性过大，为(m×max(ki))Cmax(ki)。列举其所有可能几乎是不现实的做法，所以本文决定采用Late调度算法[7]的核心观点：平均每个资源的工作时间。

分配步骤的具体算法描述为：

(1) 构造资源需要时间数组T[n][m][max(ki)]=0；

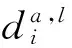
这样就构成了初始分配，我们把各个任务所需的资源映射到各个不同的单位资源上。本质上，是按所需时间从小到大排列一遍，用来使各资源的利用时间差不多相同。

接下来，我们将使用约束算法。约束算法的主要思路是在指标工作时长的情况下，把云计算多资源调度问题归约到SAT问题，用SAT问题解决调度任务的先后关系，我们将分配后的结果转化成MIN SAT SOLVER的输入。

约束算法：

定义A[r,t,s]表达是否在时间t把单位资源r分配给任务s。

定义应用程序任务流约束：

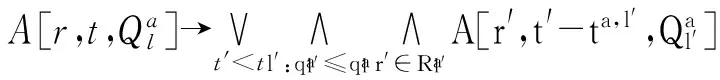
(15)

式(15)表示：如果应用程序的某一个任务所需求的资源被分配(即该任务被调度)，至少存在某一时刻，它的前驱任务所需求的所有资源被分配。

定义资源不可同时分配约束：

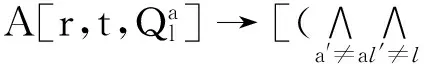
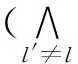
(16)

式(16)表示：如果应用程序的某一个任务所需的资源在时间t被分配，那么同时间，所有需要相同单位资源的任务都不被分配资源。

定义应用程序都完成约束:

(17)

式(17)表示：每个应用程序的最后一个任务所需的资源至少会在某个时间内分配。TIME是最长运行时长。

定义任务不可中断约束:

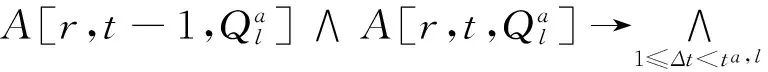
(18)

式(18)表示：如果任务在时刻被分配所需资源，且此任务的时长不为零，则资源将一直配给此任务直至结束。

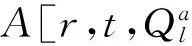
所以我们的总体算法为：

(1) 对所有任务所需求的资源进行分配；

(2) 设定TIME；

(3) 运行约束算法，生成MINI SAT SOLVER的输入；

(4) 运行MINI SAT SOLVER，如果存在满足的赋值且TIME符合要求，则返回各任务的调度时间，否则二分查找办法调整TIME跳至(3)。

这样，我们寻找到一种调度策略使工作时长尽可能短。

2.4 次优算法的算法复杂度

次优算法的分配算法的复杂度为O(N∪M(task)×|r|×log(|r|))。因为对于每一个任务需要对每个单位资源工作时间进行排序。约束算法的复杂度为(O((N∪M(task)2×T×|r|)2))。因为，为了对每个分配结果产生约束，最多需要遍历整个分配空间。

2.5 次优算法的创新性分析

本文设计的基于MINI SAT SOLVER的次优算法的创新点体现在于：

1) 调度问题与SAT求解器的结合。相比于现在比较普遍的复杂调度问题的求解方法如整数规划求解器(lpsolve、GLPK、yalmip等)，本文所使用的求解方法更加基础，在理论上研究得相对透彻。整数规划是比SAT可能要更难的问题，从而在求解专用性方面不如SAT求解器。同时在解的收敛性方面会存在不确定性，而SAT问题在定解方面会优于整数规划问题。本文为了与SAT问题进行适配，创新地将问题划分为分配和约束两个步骤，对调度问题进行了规约，比较好地利用了SAT求解器的高效性，和其定解方面的优越性。

2) 调度所涉及的模型普适性更强。本文模型囊括了多运算节点多资源有依赖的任务模型，相比于传统的单资源单运算节点有任务依赖的模型，如各种截止日期算法所针对的运算环境，和现在所研究的多运算节点多资源无任务依赖的模型，如map reduce框架下的LATE算法等。本文模型的适用面更加接近于真实环境，所研究的问题也更加复杂。所以本文创新性地做了尝试，同时解决单运算节点下多资源的约束问题、多运算节点下任务的分配问题、多任务情况下依赖调度问题。

3 实验结果与分析

3.1 测试平台及数据说明

对于基于MINI SAT SOLVER的算法测试主要是分为三大部分：1) 算法正确性测试；2) 算法优化效率部分；3) 算法的本身的运行时间测试部分。

该算法的测试主要是运用一定量的随机数据进行模拟测试，通过随机数据来突出算法在各种可能的情况下的表现。本次测试实验要模拟的数据为：

(1) 云计算多资源环境中各资源量的大小。

(2) 云计算多资源环境中所要调度的应用程序的数量。

(3) 应用程序所含任务数的大小。

(4) 各个任务本身所需要的不同资源的资源量和需要它们的时间。

本测试着重于在不同的情形中，如资源相对宽松、稀缺等，进行了评估与分析，将采用YARN默认的调度算法FIFO进行了对比，论证了其在指标工作时长下的优越性。

本测试模拟平台为单机模拟平台，主要是方便测试算法的性能。

3.2 次优算法的正确性验证

本文所选取的算法正确性验证主要方法是采取黑盒测试，输入一些指定的情况，验证其输出的正确性，具体针对归约算法里的约束算法正确性进行验证。

本文具体测试了以下的用例：

(1) 在单独一个应用程序的情况下，其中的任务，会按照任务的先后关系分配资源，即满足应用程序任务流约束。

(2) 在单独一个应用程序的情况下，其中的任务，对于所需求资源的时间不同，调度算法给出的分配答案，满足了其分配资源的时长性和时间连续性。

(3) 在两个应用程序的条件下，其中的任务，都在某一时刻前完成了，反映了调度算法满足应用程序都完成的约束。

(4) 在两个应用程序的条件下，其中的任务所需求的资源，不会在同一时刻重复分配，即满足了资源不可同时分配约束。

(5) 测试了多组、多应用程序、多任务，资源需求不同、时长也不同的用例分配结果，验证了它们同时满足所有的约束。

以上的测试用例说明了基于MINI SAT SOLVER调度算法的正确性。

3.3 次优算法的实验效果

本文选取的第一个测试用例为，云计算资源相对宽松的、各任务差异较小的情况。我们设定云包含多个资源，各资源量设定为100，应用程序数量设定为10，应用程序的任务数大小随机分布于1至3之间。任务所需要的各资源的最大资源是云平台所拥有资源的十分之一，最长任务的时长和最短任务的时长相差四倍。我们取最短任务时长为单位时长。

我们取了三组随机数进行测试，我们的调度算法是以指标工作时长为目标函数的，完成时间越短，表示性能越好。从在资源宽松的情况下的调度结果(图1)中，我们可以发现，基于MINI SAT SOLVER的调度函数优于YARN所默认的调度算法FIFO算法，平均优化的比率达到了11%左右，即完成所有任务的时间快了11%。我们认为速度上的提升是由于：1) 我们使每一个资源的平均利用时间大致相等；2) MINI SAT SOVLER求解能力的优越性。

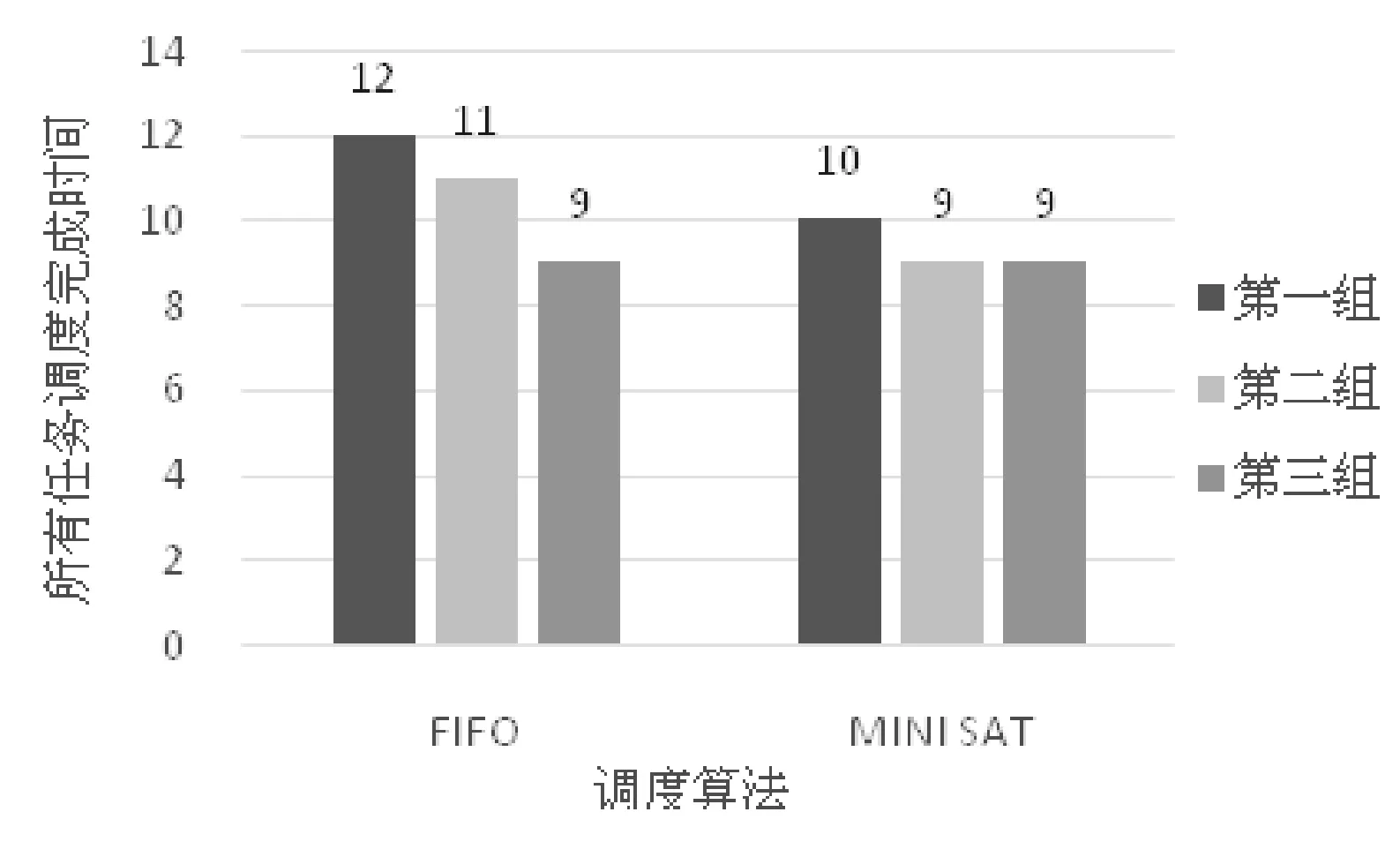
图1 资源宽松环境下基于MINI SAT SOLVER算法对比

本文选取的第二个测试为资源较为稀缺，不同任务差异较大的情况，应用程序数量设为30，应用程序的任务数大小随机分布于1至5之间。任务所需要的各资源的最大资源是云平台所拥有资源的三分之一，最长任务的时长和最短任务时长相差9倍。同样地，我们取最短任务时长为单位时长。

从图2的数据中，我们可以发现，基于MINI SAT SOLVER的次优算法远远优于YARN默认的调度算法。优化比率最高可以达到30%，如此高的优化比率得益于平均化的资源任务分配和MINI SAT SOLVER的计算能力，特别是在调度时，不同时刻对于任务时长和任务资源需求量之间选择的正确性。

图2 资源稀缺环境下基于MINI SAT SOLVER算法对比

3.4 基于MINI SAT SOLVER次优算法的运行时间

由于SAT SOLVER的技术有进一步拓展的空间，NPC难题在理论上并不能在多项式时间内解决。所以我们有必要对于SAT SOLVER的运行时间做出测试，以便确定最合理的问题规模大小。

我们认为问题规模正比于最大资源量，总任务数量的平方，以及最大任务时长的乘积。

从图3中可以看出，随着问题规模的增大，运行时间缓慢地远离线性，偏向于指数级。在我们可以接受的运行时间范围内，最好的问题规模就是介于资源宽松和资源稀缺环境下的假设规模。

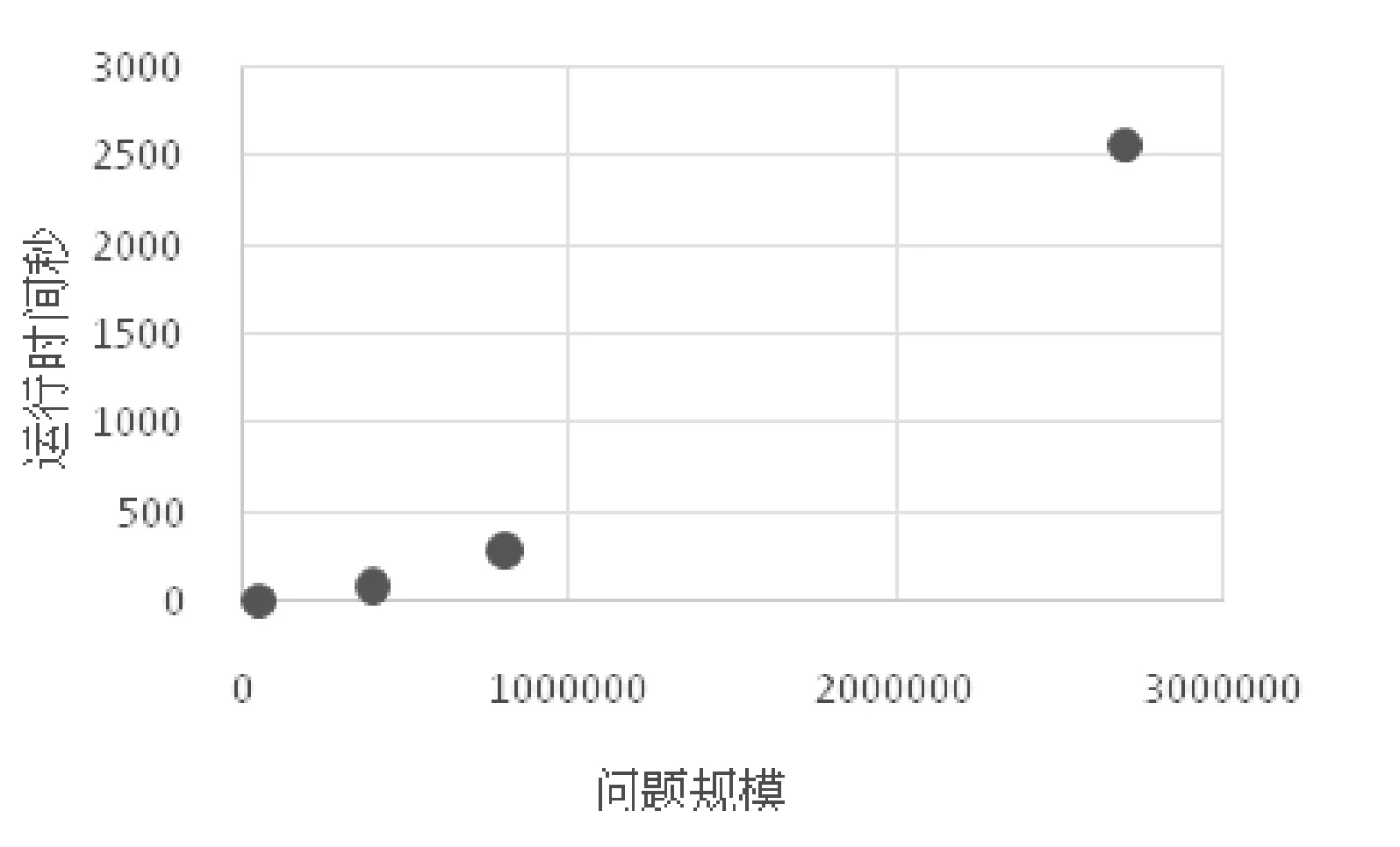
图3 MINI SAT SOLVER运行时间与问题规模的关系

4 结 语

在云计算现有的框架中，运行的应用程序包含多个任务，各个任务对资源的需求不同，并且占用资源的时间也不同。本文首先设计了云计算下资源、应用程序任务以及调度的数学模型，并对该调度模型建立了以最小化完工时间为目标的目标函数。为了对该模型进行求解，本文设计了基于MINI SAT SOLVER的次优算法，该算法有两部分组成，第一部分是分配，第二部分约束。分配部分使同质资源平均工作时长相等，约束部分通过设定调度所要满足的条件生成SAT表达式，通过求解满足表达式的最小时间变量，解决调度问题。通过模拟仿真和实验验证，在云计算资源相对宽松或稀缺的环境下，在其任务完工时间上，基于MINI SAT SOLVER的次优算法优于YARN的默认调度算法FIFO，最大的优化比率可以达到30%。

[1] Buyya R,Yeo C S,Venugopal S.Market-Oriented Cloud Computing:Vision,Hype,and Reality for Delivering IT Services as Computing Utilities[C]//IEEE International Conference on High PERFORMANCE Computing and Communications.IEEE,2008:5-13.

[2] White T.Hadoop:The Definitive Guide[M].O’Reilly Media,Inc.,2012.

[3] Kc K,Anyanwu K.Scheduling hadoop jobs to meet deadlines[C]//Cloud Computing Technology and Science (CloudCom),2010 IEEE Second International Conference on.IEEE,2010:388-392.

[4] Nieuwenhuis R,Oliveras A,Tinelli C.Solving SAT and SAT Modulo Theories: From an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL (T)[J].Journal of the ACM (JACM),2006,53(6):937-977.

[5] Davis M,Putnam H.A computing procedure for quantification theory[J].Journal of the ACM (JACM),1960,7(3):201-215.

[6] Goldberg E,Novikov Y.BerkMin:A fast and robust SAT-solver[J].Discrete Applied Mathematics,2007,155(12):1549-1561.

[7] Zaharia M,Konwinski A,Joseph A,et al.Improving MapReduce Performance in Heterogeneous Environments[C]//OSDI’08 Proceedings of the 8th USENIX conference on Operating systems design and implementation. San Diego,California—December 08-10,2008:29-42.

A MULTI-RESOURCE SCHEDULING ALGORITHM FOR MINIMIZING MAKESPAN IN CLOUD COMPUTING

Yang Peng1Jin Dan1Zhang Sheng2Xu Xin2Yao Jianguo2

1(InformationandCommunicationCompany,StateGridGansuElectricPowerCompany,Lanzhou730050,Gansu,China)2(ShanghaiJiaoTongUniversity,Shanghai200240,China)

The default FIFO scheduling on the Hadoop platform in cloud computing is targeted at fairness, however, considering a single factor will make the resource utilization is low and the task is completed too long. The makespan is more important in trade-off between fairness and makespan. On this basis, we established the multi-resource and application tasks and the scheduling mathematical model and its objective function under cloud computing, and we used the reduction method and MINI SAT SOLVER with powerful computing ability to solve the problem. The simulation results show that the suboptimal algorithm based on MINI SAT SOLVER is shorter than the default scheduling algorithm FIFO in YARN under different resource supply conditions, and the optimization ratio can reach 30%.

Cloud computing Scheduling algorithm NP-Complete problem Makespan

2016-10-21。国家自然科学基金项目(61303013)。杨鹏，高工，主研领域：协议分析。靳丹，教授级高工。张晟，硕士生。徐鑫，硕士生。姚建国，副教授。

TP3

A

10.3969/j.issn.1000-386x.2017.07.001