基于图形绘制技术的杨林岩水道右岸边滩模拟及分析

朱梅

摘 要：工程竣工前测量，主要用于确实掌握工程整治建筑物结构稳定情况，为工程竣工验收提供依据。用三维模拟软件，能更加清晰地反映施工前后的地形变化情况，反映施工的效果，为下一步施工方案寻找依据。随着测量技术、图像处理技术、数据分析技术的迅速发展，利用MATLAB软件图形处理技术来解决问题成可能。因此，深入研究基于河床演变分析方法，是十分必要的。针对常规分析方法的不足，对基于图形绘制技术的河床演变分析方法进行了深入研究。本文利用MATLAB软件的三维绘图技术，根据14年、15年费家墩工程区施工前后的测量数据，给杨林岩水道右岸边滩做出模拟分析。

关键词：河床演变 MATLAB分析

一、航道概况

1.1 河道基本情况

杨林岩水道位于长江中游，湖北省洪湖市、湖南省岳阳市境内，上邻洞庭湖湖口与荆江下口，距城陵矶15km，下接界牌水道，距武汉217km。该水道位于中游航道里程210～217km，河段上至擂鼓台、下止杨林山，属顺直分汊型河段。河段自上而下依次分布有白螺矶～道人矶、杨林山～龙头山对峙节点，使河段平面形态呈宽窄相间的藕节状。在白螺矶～道人矶处河宽为1.75km，杨林山～龙头山处河宽为1.12km，在上下节点中间，河段宽阔，出现洲滩，白螺矶～道人矶上游仙峰洲（丁家洲边滩）处最大河宽为2.49km，而南阳洲汊道段最大河宽达3.2km。

河段上段较为顺直，主流偏右，右岸多礁石；下段被南阳洲分为左右两汊，多年来河势较为稳定，右汊为主通航槽。

该河段目前航道尺度为3.5m×80m×750m（水深×航宽×弯曲半径），实行分月维护水深。随着沿江经济及长江航运的快速发展，航运需求大幅提升，地方政府多次要求提高长江航道维护尺度。为适应地方经济发展、尽早实现规划航道尺度，交通运输部安排了长江中游杨林岩水道航道整治工程对该河段进行整治。

1.2 碍航特性简况

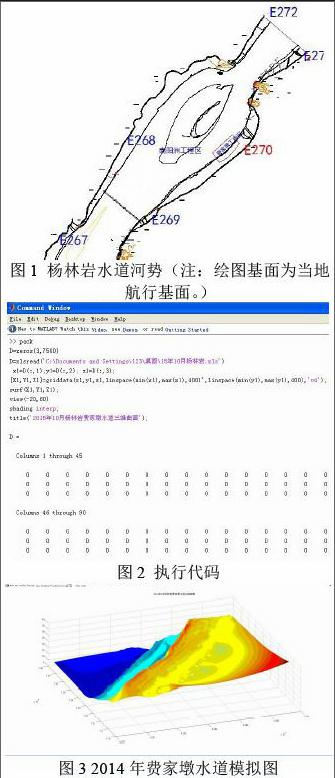
工程河段以道人矶～白螺矶对峙节点为界，分为上下两段。上段顺直，两岸有大堤保护，多年来河床稳定少变，下段河道放宽，江中南阳洲分河道为左右两汊，多年来河势基本稳定。三峡蓄水前，在不同水沙条件下，南阳洲淤长冲刷，洲头上提下移，左右汊冲淤调整，部分时段航道条件较差，但洲滩在自然演变下能够恢复。三峡蓄水后，水沙条件发生改变，河段总体冲刷，特别是近年来河床演变逐渐加快，南阳洲洲头持续冲刷下退、南阳洲右缘崩退，以及相应的左岸丁家洲边滩下延，左汊有所冲刷，右汊展宽。南阳洲作为重要洲滩，滩体受冲刷有所缩小，工程河段滩槽逐渐坦化，滩槽格局和航道条件已明显表现出向宽浅化方向发展的不利趋势。三峡蓄水后的水沙条件今后将继续保持，任其自然演变，滩槽格局不利的变化趋势将进一步发展，目前较好的航道条件将有逐步变坏甚至恶化的可能。所以交通运输部安排了长江中游杨林岩水道航道整治工程对该河段实施整治，以稳定目前相对较好的航道条件和滩槽格局。河道形势见图1。

二、分析工具

MATLAB是Math Works公司开发的数学分析软件，具有强大的三维绘图与数据分析能力。[2]MATLAB产品族可进行以下工作：数值分析、计算、工程与科学绘图、控制系统的设计与仿真、控制系统的设计与仿真、数字图像处理、数字信号处理。MATLAB的应用范围非常广，包括信号和图像处理、通讯、控制系统设计、测试和测量、金融建模和分析等众多应用领域。附加的工具箱（单独提供的专用MATLAB函数集）扩展了MATLAB环境，以解决这些应用领域内特定类型的问题。根据费家墩工程区2014年3月和2015年10月两个测次的水深数据，图比1：1000、测区面积约0.7 km2，我们可以利用MATLAB模拟费家墩工程区河道的三维水深图像。

2.1 MATLAB在地形处理方面的相关函数。

MATLAB主要包括核心函数和工具箱，在地形处理方面，常用函数有：interp1、interp2、griddata，mesh和surf。[1]本文采用的是griddata。

（1）yi=interp1（x，y，z，xi，yi，method）是用于確定边界点位置的一维插值函数， x，y为已知坐标向量， xi为需插值坐标向量，method为插值方法。MATLAB提供了4种插值法：nearest，linear， spline和cubic。

（2）zi=interp2（x，y，z，xi，yi，method）是根据有结构四边形网格数据点插值的二维插值函数，x，y，z为已知坐标矩阵，且x和y为单调向量，xi，yi为需插值坐标矩阵，zi为插值结果。若已知矩阵形式的地形数据，则此函数是比较理想的插值方法。

（3）zi=griddata（x，y，z，xi，yi，method）是根据离散数据点插值的二维插值函数，其变量含义与 interp2类似，但x和y可以为非单调向量，因而可进行离散数据点插值。

（4）mesh（x，y，z）和surf（x，y，z）为常用的地形重现函数，mesh函数用于生成反映网格式格布设的网眼图，surf函数用于生成表现地形形态的三维色带图。

2.2 数据前处理。

地形测绘技术从人工测绘发展到GPS及遥感测绘，前后数据形式的差别较大。从目前数据形式看，大致可以分为：零散人工观测数据、图纸数据和电子地图。本文采用的是第三种，即原始数据为grp格式的电子数据。

首先将grp格式原始资料转换成TXT格式，再将TXT格式转换成Excel格式。用测量学闭合差法进行数据清洗，删除不合理数据，得到每个数字均为有效数据的Excel文件。

三、图像生成

3.1 2014年3月费家墩工程区三维图

编辑代码如下：

代码解释：

由于14年3月的测量数据有7400个三维高程点，代码中，先预分配分配一个3X7500的矩阵D。再将excel格式的测量数据赋值给矩阵D，最后利用griddata绘图函数进行绘图。执行代码输出结果为图3。

模拟图用颜色直观标示了高程高度：颜色越接近红色，水深越深；颜色越接近深蓝色，水深越浅。根据模拟图可以看出：费家墩工程区东高西低，越往下游水深越浅。

3.2. 2015年10月费家墩工程区三维图

编辑代码如下：

执行代码输出结果为图5。

3.3 数据比对

利用差值法，将2015年9月测图数据与14年3月数据进行对比分析。差值法，即事先进行数据清洗，得到两个测次高程差的有效数据。该方法与surfer网格法相比优势在于：清洗掉了无效数据，避免两个测次的测量数据坐标范围不完全相同时，由于对比数据不齐全造成失真现象。通过比对分析两次观测数据，费家墩工程区水域的数据变化情况如下图所示：

从图中可以看出，整个测区水底地形变化以降低为主，淤积主要发生在x坐标7200-7225，y坐标4290-4296的范围内。其中，护岸主体部分地形稳定，护岸近江心侧地形也表现出较为稳定的状况，远离护岸的水底部分存在变低趋势。伴随着工程区左测的淤积下延，费家墩工程区自上而下发生冲刷，冲刷下移的泥沙，淤积在中下段，形成浅区，形成交错浅滩，且下深槽仍处于不断萎缩后退中。

3.4 调试问题

（1）原始数据格式问题。用Excel导入TXT数据时选择“数值”模式，结果生成的Excel表格无法被MATLAB打开；选择“常规”模式后，结果生成的Excel表格可以被MATLAB读取。Excel表格要存成2003版本，比较方便数据读取。

（2）内存不够问题。由于处理数据量较大，只有32位xp计算机上2G内存，实验过程总会提示内存不够。因此，采取以下措施。1.给处理数据预先分配连续的存储空间。2.通过修改内存设置扩展物理地址，并且通过修改用户配置文件将电脑启动为3G模式，可以增大内存空间。3.常用pack命令，可以释放不连续的内存空间，为运行程序腾出空间。

四、总结与展望

通过模拟，可得出如下结论和建议：

4.1 MATLAB是良好的模拟分析工具

由于其强大的数据分析能力，可以作为分析河床变化的辅助工具。其优点有：（1）具有很好的图形处理能力，提供大量的三维图形函数，数学函数可用于线性代数、统计、傅立叶分析、筛选、优化以及数值积分等。正是这种能力为数据的图形化标示提供了有力工具，三维图形函数可用于可视化数据，使数据的展示更加形象生动。（2）与C语言有良好的接口。各种函数可将基于MATLAB的算法与外部应用程序和语言（如 C、C++、Fortran、Java、COM 以及 Microsoft Excel）集成。在本次实验中，由于数据较多，MATLAB的字符处理能力较欠缺，因此用C语言先读入excel数据，再由MATLAB绘图。

（3）有强大的工具箱，提供各种模拟、分析工具，有利于揭示数据间的内在关系，有助于发现河道变化规律。（4）此高级语言可用于技术计算，此开发环境可对代码、文件和数据进行管理。

4.2 可对比不同分析方法

目前，研究区域的冲淤量确定可采用三角网法、栅格法和等值线法：三角网法采用直接以离散点构造三角形进而形成三棱柱的方法来计算冲淤量具有计算速度快，精度高等特点；栅格网法不但可以保证河床冲淤演变的精度，还能够准确地给定不同位置处的冲淤变化情况，故栅格网法是一种比较确、全面的分析方法。等值线法具有数据量小，计算速度快等特点，但冲淤量的确定精度与给定等值线的精度和密度有关，等值线的精度越高，密度越大，冲淤计算的精度越高。[1]不同分析方法的比较可以作为下一步研究方向。

4.3更多显示分析模型

（1）更多显示函数可以帮助表达分析：1.函数colorbar在当前的图形窗口中增加水平或垂直的颜色标尺以显示当前坐标轴的颜色映象；2.灯光设置light指令，使用后，原为强度相等的漫射光，后为面等子对象有关光的属性都被激活；3.hidden off透视被叠压的图形。

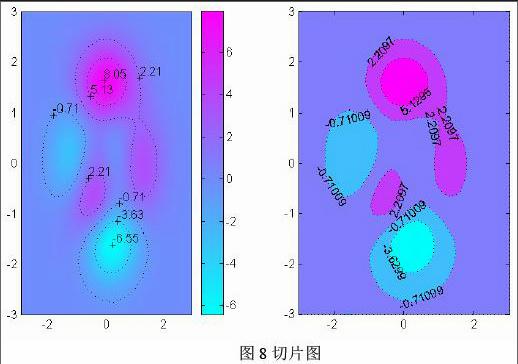
（2）高维可视化。二维半图指令pcolor， contour， contourf，可以将冲淤图分析做成如图8的切片图。

（3）准四维表现，用颜色表现函数的其他特征（如梯度、曲率等）。引入时间变量，可以直观反映变化的缓急程度。

4.4利用学习型算法

随着测绘基础数据的累积，机器学习算法可以被应用到河床变化分析中。无监督学习（Unsupervised learning）就是聚類，事先不知道样本的类别，通过某种办法，把相似的样本放在一起归位一类；而监督型学习（Supervised learning）就是有训练样本，带有属性标签，也可以理解成样本有输入有输出。[3]可以利用无监督型学习中的聚类算法，分析河床变化和水情气象之间的内在联系，为河床演变预测提供更多依据。

参考文献

[1]张红梅，基于图形绘制技术的河床冲淤演变定量分析方法，武汉大学学报，2005-02.

[2]张志涌，杨祖缨，《MATLAB教程》，北京航空航天大学出版社，2010.

[3]）Tom Mitchell，《机器学习，机械工业出版社，2008.