冲击波作用下微米尺度金属颗粒群的动力学行为∗
2017-08-09赵信文李欣竹张航王学军宋萍张汉钊康强黄金吴强
赵信文 李欣竹 张航 王学军 宋萍 张汉钊 康强 黄金 吴强
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理重点实验室,绵阳 621900)
冲击波作用下微米尺度金属颗粒群的动力学行为∗
赵信文 李欣竹†张航 王学军 宋萍 张汉钊 康强 黄金 吴强
(中国工程物理研究院流体物理研究所,冲击波物理与爆轰物理重点实验室,绵阳 621900)
(2016年11月11日收到;2017年2月28日收到修改稿)
基于平面化爆驱动飞片高压加载技术和激光测速技术,研究了冲击波加载不同粒径锡颗粒群的微喷射行为以及在空气中的减速规律.实验结果表明,锡颗粒的最快喷射速度随粒径增大而显著增大.通过对微喷射形成过程的三维光滑粒子流体动力学方法数值模拟发现,大粒径锡颗粒之间存在较大的空隙结构,冲击波与空隙结构的相互作用诱导产生高速汇聚射流,空隙结构越大对应的喷射速度也越高.此外,通过研究不同粒径颗粒在复杂流场中的减速规律,进一步深化了对微喷射破碎后的颗粒尺度状态以及混合输运特性的认识.研究结果对于预测和分析冲击波加载微米颗粒群的微喷混合特性具有一定价值.
∶微米颗粒,微喷射,最快喷射速度,减速特性
PACS∶47.15.Uv,62.50.Ef,47.11.—jDOI∶10.7498/aps.66.104701
1 引 言
存在表面缺陷(如车削加工痕、空泡、杂质等)的材料在冲击波作用下,会喷射出少量高速颗粒态物质,即所谓的微喷射现象[1−6].该现象广泛存在于冲击动力学过程中,并在众多技术应用领域具有关键的影响作用.例如,在激光间接驱动惯性约束聚变(inertial confinement fusion,ICF)中,激光冲击加载诱导的多层靶界面间发生的大尺度密度不均匀和中小尺度材料混合是影响聚变点火成功的关键因素[7].在极端条件下的材料界面诊断中,微喷射现象的发生会严重影响如高速摄影[8]、激光测速[9]/测距[10]、界面测温[11,12]等技术的测量精度,部分情况下界面信息甚至被微喷物完全掩盖而无法实现有效诊断.开展深入的材料微喷混合问题研究在工程技术应用领域具有重要意义.
在微喷混合问题的研究中,利用冲击波加载金属颗粒群来产生特定的微喷射状态是一种重要的实验技术.由于其喷射状态相对简单可控,该类实验被广泛用于微喷混合测试系统的不确定度评估、颗粒在气体中的混合输运特性研究,以及混合输运模型检验等.2006年,马云等[13]采用冲击加载面密度经过精确标定的铝粉颗粒群的方法,标定了Asay[14]膜技术测量微喷颗粒总质量的不确定度.2012年,Oró等[15]开展了爆轰加载铝基板表面粘附微米尺度钨粉的模拟喷射实验,研究钨颗粒分别在真空、氩气、氙气中的混合输运过程,并以此来校验并改进其发展的颗粒输运模型.2015年,Rousculp等[16]在PHELIX磁驱装置上开展了柱面粘粉实验,研究柱面汇聚条件下钨颗粒在氩气和氙气中的混合输运特征.虽然粘粉类实验技术已被广泛使用,但目前针对冲击波加载金属颗粒群产生微喷射过程的物理机理和喷射特性的研究相对较少,尤其是缺乏初始颗粒粒径、材料物性、加载压力等对喷射状态影响的系统性认识.在上述研究工作中,通常需要靠人为经验给出冲击加载后的颗粒尺度及其对应的初始速度等,缺乏相应的物理依据.因此,有必要对冲击波作用下金属颗粒群的动力学行为开展深入研究.
本文对冲击加载金属颗粒群产生微喷射过程的物理机理开展了初步研究,并重点考察了初始颗粒粒径对加载后喷射物的速度和颗粒尺度的影响.实验采用化爆驱动飞片技术冲击加载四种不同粒径的锡颗粒产生喷射状态,利用任意反射面位移干涉激光测速(DISAR)技术[9]测量了微喷物颗粒在空气中的减速规律,并通过分析其减速特征,给出破碎后的颗粒度状态.同时,利用三维光滑粒子流体动力学方法[17,18](smoothed particle hydrodynamics,SPH),对锡颗粒的高速喷射过程进行了定性模拟,分析了初始颗粒粒径对最快喷射速度和空间物质分布的影响.该工作为粘粉类微喷实验设计及结果分析提供了一定的参考.
2 基板粘粉模拟微喷射实验
本文采用化爆驱动飞片的方式产生平面高压加载,实验系统见图1.具体为单根雷管起爆一块铝基平面网络起爆板(厚8 mm,装药为1 mm厚的GI-920)产生平面爆轰波,进而引爆TNT主炸药(ϕ100×20 mm)作为飞片驱动源.主炸药与钽飞片(ϕ70×2 mm)之间预置1 mm 空气间隙以减弱爆轰波引起的飞片变形,TNT爆轰产物驱动飞片在空气中加速22 mm后加载到钛基板(15 mm厚)上,形成约30 GPa的平面冲击波.在钛基板自由面一侧预置不同粒径的锡粉,冲击波加载锡粉并使其以高于基板自由面的速度喷出.实验中利用DISAR技术测量了冲击波加载不同粒径锡粉后产生的微喷射颗粒在空气中的减速特征.
在冲击波加载含缺陷金属表面诱导的微喷混合问题中,微喷物的颗粒尺度一般在数十纳米到十几微米之间[19].采用粘粉实验技术来模拟实际的金属微喷射过程时,其喷射状态应尽量接近.对此,本文选取了四种直径分别为(0—0.1),(0.5—1),(5±1),(10±1)µm的准球形锡粉颗粒(在相应尺寸范围内的粉体质量分数大于90%)作为研究对象,来对比不同初始颗粒粒径对微喷射状态的影响.此外,由于粘粉面密度也是影响喷射特性的主要因素,实验中需要对粘粉面密度进行准确的测量并保证其尽量接近.对比本文利用在高光洁钢膜上粘粉的方式实现.具体方法为∶在ϕ12×0.2 mm的高光洁钢膜表面均匀涂覆一层极薄的真空油脂,将油脂量控制在粘粉总量的5%以内,之后在油脂表面均匀喷洒不同粒径的锡粉,利用高精密电子天平(BP01D)分别对涂抹油脂和粘粉后的钢膜样品称重,从而计算得到粘粉面密度,结果如表1所列.最后将制备的粘粉样品粘接在钛基板ϕ20 mm的圆周上.
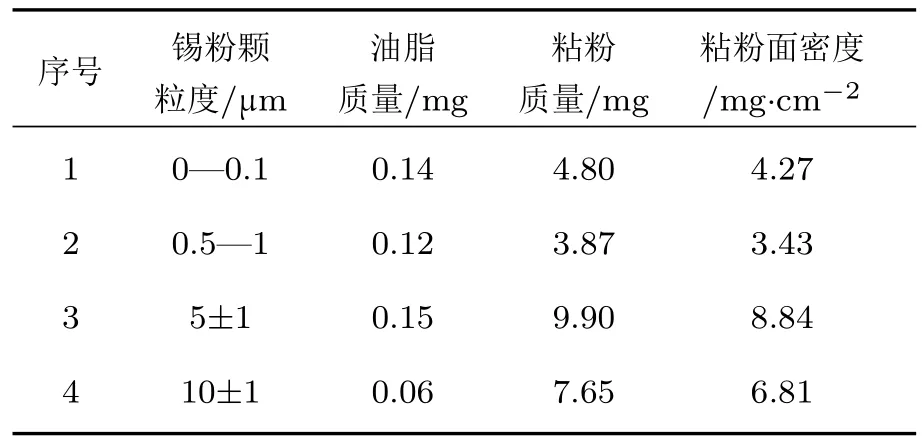
表1 粘粉状态Table 1.The state of the pasted Sn particles.
3 结果与分析
3.1 加载动力学状态
加载动力学状态是影响颗粒群微喷射行为的关键因素,需开展详细的分析.图2为DISAR测量的钛基板中心点自由面卸载的速度频谱结果.在56µs前钛基板自由面速度出现缓慢上升,这是因为整个实验在大气环境中开展,钽飞片在碰撞钛基板前驱动空气产生的气体冲击波在钛基板中提前形成弱加载.飞片加载后钛基板自由面卸载速率峰值为2.07×103m/s,利用冲击波关系(1)式可计算得基板中近自由面的加载峰值压力为30.8 GPa.
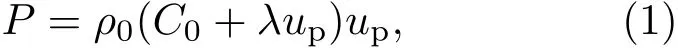
其中,P为冲击波压力;ρ0为材料密度;C0和λ为冲击波和粒子速度的线性相关系数,相关材料参数见表2;up为材料中波后粒子速度,根据冲击波在自由面卸载的波后粒子速度与自由面速度的近似关系式[20],波后粒子速度约为自由面速度的一半,在本实验中up为1.035×103m/s.由于本文实验中采用的钽飞片厚度远小于钛基板厚度,加载后形成的方波受后向稀疏波影响而转变为三角波,这使得自由面速度快速下降并使钛基板发生层裂,根据(2)式层裂厚度近似关系[21]可计算得层裂片厚度约为1.5 mm.

其中,δ为层裂片厚度,Cb为卸载后的材料体波声速,本文取6.16×103m/s;∆t为自由面速度振荡周期,在本实验中约为0.5µs,见图3.
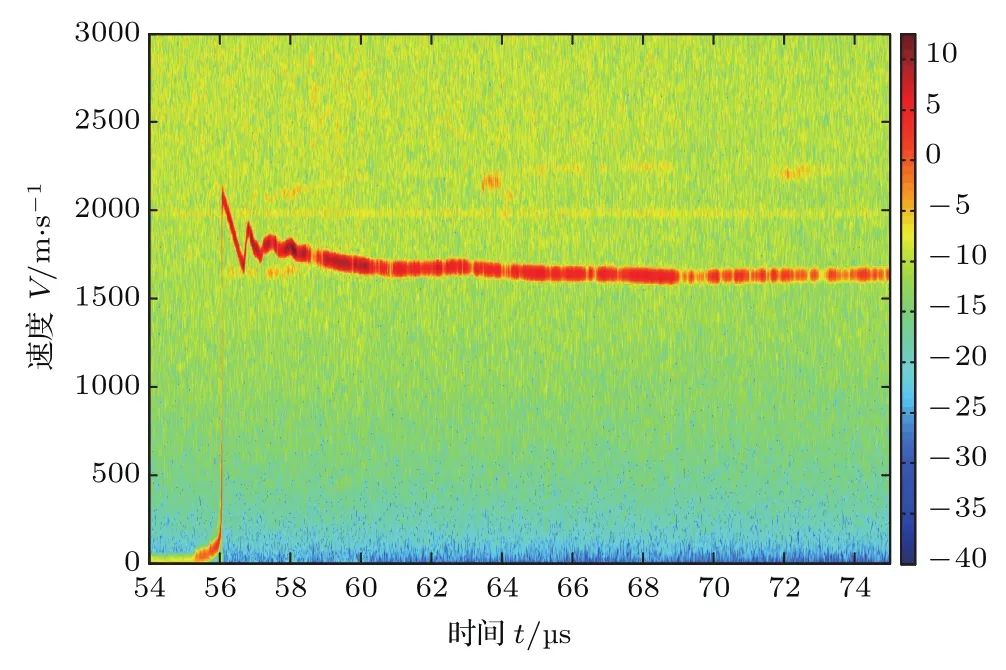
图2 (网刊彩色)钛基板自由面卸载速度曲线Fig.2.(color online)Measured velocity of the Ta surface versus time.
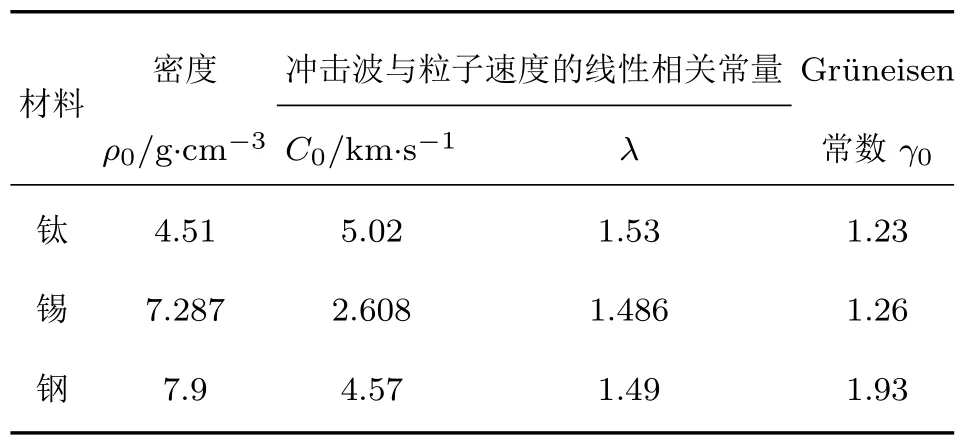
表2 材料参数Table 2.Parameters of Ti,Sn and steel.
从图3局部放大的钢膜自由面速度图像中可以看出,钢膜卸载时自由面首次起跳速度约为1.48×103m/s,利用阻抗匹配法[20]计算得对应加载到密实态锡中的压力约为25 GPa,略高于锡的卸载熔化压力(20—25 GPa).事实上,由于实验中锡粉为松堆积状态,约为密实态锡体密度的30%—50%,冲击波加载到疏松态锡颗粒群中的温度会更高,并使其发生卸载熔化.
为方便对实验结果的分析解读,本文利用Autodun软件对加载动力学状态进行了模拟,材料参数选自软件自带材料库,计算结果如图3所示.图中将飞片、自由面的初始起跳时间均调整为零点.从图中可以看出,数值模拟给出的自由面卸载速度曲线与实验结果符合较好,说明数值模拟结果可信.数值模拟得到的钽飞片碰撞速度为1.5 km/s,钛基板中心位置的冲击波压力峰值为31.2 GPa,层裂片厚度约为1.8 mm,与实验基本相符.此外,数值模拟结果表明,当冲击波在基板自由面卸载时,钛基板ϕ20的位置已经受到边侧稀疏波的影响,该区域的加载压力略低于中心点.
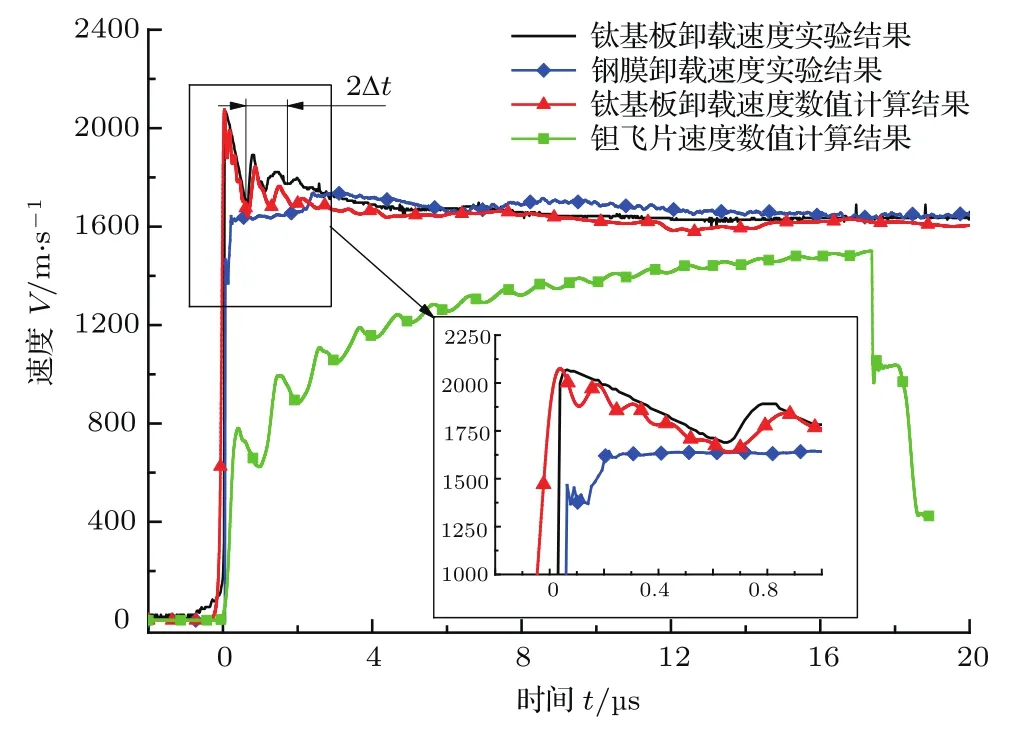
图3 (网刊彩色)钛自由面速度和钽飞片速度的数值模拟结果Fig.3.(color online)Simulated velocity of Tifree surface and Tafl yer.
3.2 最快喷射速度
图4为采用DISAR技术测量的冲击波加载不同粒径锡颗粒产生的微喷射颗粒群在空气中的减速曲线,其中1µm颗粒状态的信噪比相对较差.对比四个测点喷射物速度首次起跳时刻,同步性优于50 ns,说明本文实验具有很高的周向加载均匀性.此外,由于0.1µm和1µm颗粒的尺度较小,DISAR技术采用的探测光(波长1550 nm)对该尺度颗粒的穿透性相对较强,因此,在其速度频谱中能同时观测到喷射物速度和钢膜的运动速度信息.
从图4中可以看出,锡粉颗粒在冲击波作用下以远高于钢膜自由面的速度喷出,并且最快喷射速度随颗粒粒径的增大而增大,其中0.1µm和1µm颗粒的最快喷射速度相近,约为1.74倍的Vfs(Vfs为钢膜自由面卸载首次起跳速度,本实验中为1480 m/s),5µm颗粒为2.2 Vfs,10µm颗粒为2.6 Vfs.通过对比分析发现,在颗粒粒径为5µm和10µm状态时,钢膜表面密排的锡颗粒之间组成尺度较大的空隙结构,见图5,微喷射现象即来源于冲击波与这些空隙缺陷的相互作用,而且粒径越大颗粒间的空隙结构也越大,诱导产生的喷射物速度也就越高.而在0.1µm和1µm状态时,这种颗粒间的亚微米尺度缺陷对微喷射的影响很小,此时的喷射物主要来源于颗粒群构成的微米尺度缺陷结构,因此在最快喷射速度上两者相差不大.
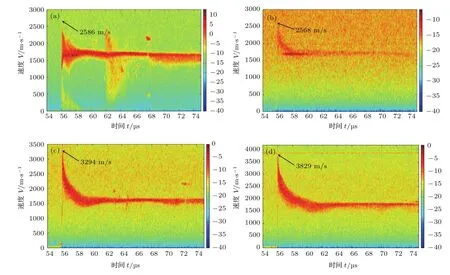
图4 (网刊彩色)冲击波加载不同粒径锡颗粒的微喷射速度 (a)0.1µm;(b)1µm;(c)5µm;(d)10µmFig.4.(color online)Measured velocities of micro-ejecta with different particle sizes:(a)0.1µm;(b)1µm;(c)5µm;(d)10µm.
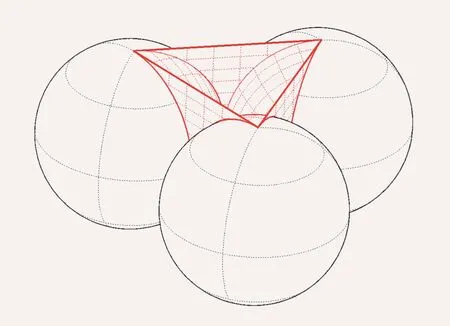
图5 (网刊彩色)颗粒间空隙结构示意图Fig.5.(color online)The profile of the gap among Sn particles.
为进一步验证上述微喷射产生的机理,本文利用三维SPH方法模拟了冲击波加载锡颗粒群诱导的微喷射形成过程.针对SPH算法,Liu等[17]在其著作中给出了详细的介绍,本文不再赘述.由于实际样品表面的颗粒堆积状态非常复杂,数值模拟很难完整地复现实验状态,对此本文只对5µm和10µm的两种大颗粒组成的典型缺陷结构进行定性模拟.数值模拟采用的简化物理模型为∶设定一刚性固壁以890 m/s的速度加载不同粒径的锡颗粒,对应加载到密实态锡中的压力为25 GPa.同时,考虑到冲击波加载后锡颗粒群发生卸载熔化,在计算中不考虑锡的强度影响.计算采用的材料参数见表2,SPH单元尺寸为0.2µm.
从图6中可以看出,在冲击波作用下,颗粒间的空隙位置产生了高速汇聚射流,10µm状态的射流头部速度达到约5 km/s,5µm时约为3.8 km/s,模拟结果与实验结果定性一致.这证实了当颗粒尺度较大时,冲击波与颗粒间缺陷结构的相互作用是微喷射产生的主要原因,同时也解释了最快喷射速度随颗粒尺度增大而显著增大的物理机理.
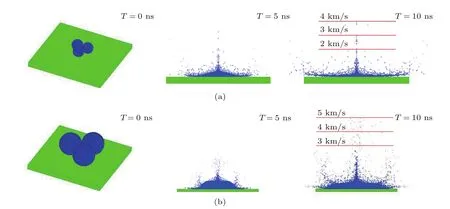
图6 (网刊彩色)冲击波与颗粒空隙相互作用诱导的微喷射形成过程 (a)5µm;(b)10µmFig.6.(color online)Temporal evolutions of the micro-ejection induced by the interaction of gaps among particles with different sizes:(a)10µm;(b)5µm.
3.3 微喷射前端颗粒减速
金属微喷射研究表明,冲击波与表面缺陷诱导的微射流在演化过程中受速度梯度、气动力、表面张力等影响,会迅速断裂/破碎成颗粒态[22],并在气体中减速.图7给出了冲击波加载四种粒径颗粒产生微喷射前端颗粒在空气中的减速曲线,该速度曲线为图4中颗粒群速度频谱的上沿.从图中可以看出,四种颗粒尺度状态的微喷射前端颗粒减速规律基本一致.在初始阶段,由于微喷射头部颗粒速度要远高于钢膜运动产生的气体冲击波速度(本文中约为2100 m/s),这时颗粒在静止气体中运动,与气体的相对速度差约8—11Ma,在气动阻力作用下颗粒速度迅速下降.随后,颗粒持续减速并当其空间位置处于气体冲击波波后时,颗粒速度与波后气体速度差减小,速度趋于恒定.
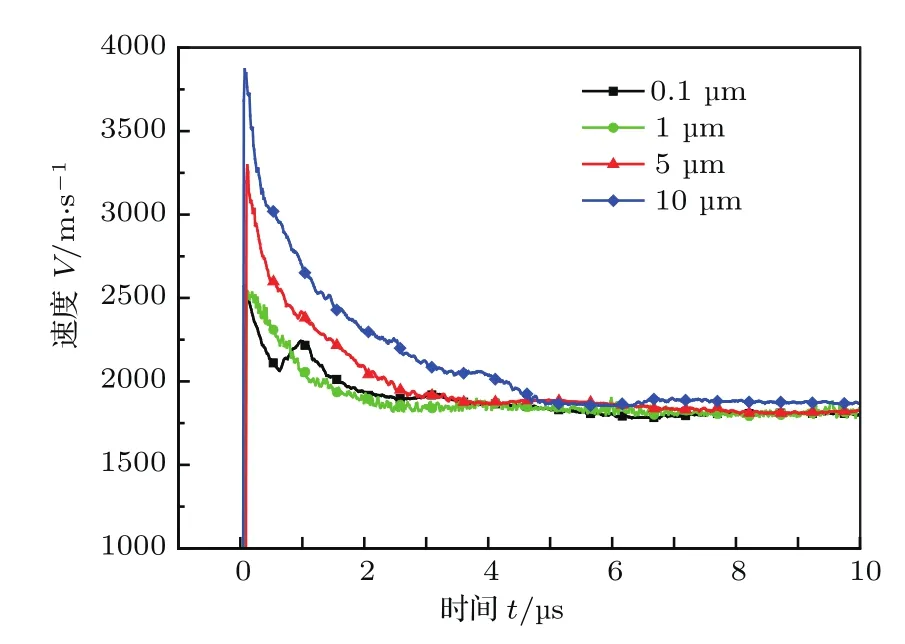
图7 (网刊彩色)不同颗粒状态诱导喷射的前沿颗粒减速曲线Fig.7. (color online)Temporal evolution of tipvelocity of micro-ejecta particles with different sizes.
同时,在0.1µm颗粒状态减速曲线的1µs时刻有一个较弱的速度回跳,结合钛基板自由面的速度曲线分析,这极有可能是因为钛基板层裂片的速度回跳对锡粉造成二次加载,产生了新的高速微喷颗粒[23].然而,在其他尺度的颗粒状态中却并未观测到该现象.正如前文提到的DISAR探测光对0.1µm颗粒群具有良好的穿透性,因此能捕捉到这种发生在钢膜近表面的二次加载效应,而在其他尺度的颗粒状态下DISAR探测光被前端高速喷射物遮挡而未观测到该信号.目前,对二次加载产生微喷射现象的物理认识还不完善,有必要在后续工作中开展进一步的研究.
3.4 微喷射颗粒尺度及其混合输运
在微喷混合问题研究中,微喷物的颗粒尺度及其在气体中的混合输运行为也是目前关注的重要内容.为进一步了解粘粉实验中喷射物的颗粒尺度及其输运过程,本文采用拉格朗日框架下的颗粒轨道模型来模拟不同粒径颗粒在复杂流场中的运动.针对该模型Fung等[24]以及王裴等[25]给出了详尽的介绍,本文不再赘述.在此,需要指明的一点是,本文计算中颗粒在气体中运动受到的气动阻力系数,采用Igra等[26]基于激波管实验拟合得到的阻力系数公式得到,见(3)式,文献中指出该公式可较为可靠的应用于200≤Re≤10100的强可压缩超音速流动条件.其中,Cd为阻力系数,Re为雷诺数.
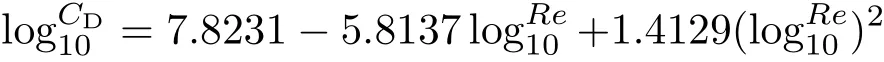

本文的基本思路是计算不同粒径颗粒以不同的初速度在钢膜推出气区流场中运动,选择合适尺度和初速度的颗粒减速曲线来拟合实验测量结果.两相流研究表明,相同初始条件下粒径越大的颗粒减速越慢,利用该方法可近似给出不同初始喷射速度下的前端颗粒尺度上限,计算结果如图8所示,图中D为颗粒直径,Vini为颗粒初始速度.
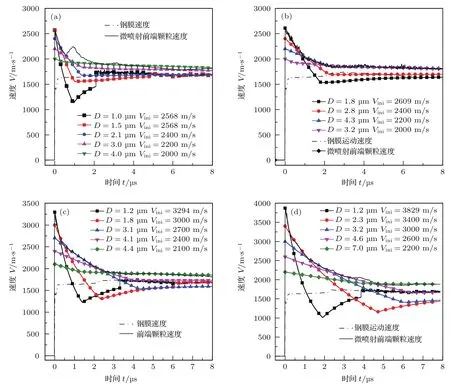
图8 (网刊彩色)数值模拟的不同粒径颗粒减速曲线 (a)0.1µm;(b)1µm;(c)5µm;(d)10µmFig.8.(color online)Simulated transport velocity for different particle sizes:(a)0.1 µm;(b)1 µm;(c)5 µm;(d)10 µm.
从对冲击波加载不同粒径的锡颗粒诱导产生的微喷射前端颗粒减速曲线的拟合结果来看,喷射速度越高的颗粒其尺度越小,从微喷射头部到低速区颗粒尺度依次增大,这与Sorenson等[22]利用超高分辨率全息照相技术获得的颗粒尺度分布结果一致.进一步对比喷射物的颗粒尺度发现,5µm和10µm颗粒在加载后形成的喷射物颗粒尺度总体减小,而0.1µm和1µm的颗粒在加载后其喷射颗粒尺度反而增大.如前文所述,大尺度颗粒的喷射物来源于冲击波与颗粒空隙缺陷的相互作用,其射流体尺度本身要小于初始的锡颗粒尺度,并在自身速度差及气动力作用下进一步发生了破碎.而小尺度颗粒的喷射物主要来源于颗粒群组成的大尺度缺陷,卸载熔化后的锡颗群存在一定的聚合.
对不同粒径颗粒的减速特征模拟结果表明,微喷射颗粒群在减速过程中,小尺度颗粒的空间位置逐渐落后于大尺度颗粒,DISAR技术测量的前端减速曲线,实际上是不同粒径颗粒速度耦合的结果.此外,分析图8(a)中数值计算给出的1µm尺度颗粒的减速过程发现,微喷射前端的高速小尺度颗粒在初始阶段速度高于气体冲击波速度,并在静止流场中快速减速,当其空间位置处于波后气体流场时,在气动力作用下颗粒被再次加速.该过程正好与图4(a)中56—58µs之间钢膜速度频谱下方先减速后加速的速度频谱结果相符.同时,模拟结果显示部分减速过快的颗粒在运动过程中会重新回贴到钢膜上.
4 结 论
本文研究了冲击波加载不同粒径微米锡颗粒群的微喷射行为,发现初始锡颗粒尺度对微喷射过程有显著影响,颗粒粒径越大产生的微喷射速度越快,破碎后的颗粒尺度也相对较大.通过对微喷射形成过程的SPH模拟,揭示了微喷射产生的机理,及最快喷射速度随颗粒尺度变化的原因.此外,基于颗粒轨道模型进一步模拟了不同粒径颗粒在复杂流场中的减速特性,并通过与实验结果对比,初步给出了微喷颗粒的尺度分布状态.上述结果可用到粘粉类微喷射实验设计和分析,以及颗粒在气体中的混合输运过程研究等方面.
[1]Walsh J M,Shreffler R G,WillingfJ 1953 J.Appl.Phys.24 349
[2]Asay J R,Mix L P,PerryfC 1976 Appl.Phys.Lett.29 284
[3]Wang P,Qin C S,Zhang S D,Liu C 2004 Chin.J.High Press.Phys.18 149(in Chinese)[王裴,秦承森,张树道,刘超2004高压物理学报18 149]
[4]Buttler W T,Zellner M B,Olson R T,Rigg P A,Hixson R S,Hammerberg J E,Obst A W,Payton J R 2007 J.Appl.Phys.101 063547
[5]Monfared S K,Oró D M,Grover M,Hammerberg J E,Lalone B M,Pack C L,Schauer M M,Stevens G D,Stone J B,Turley W D,Buttler W T 2014 J.Appl.Phys.116 063504
[6]Durand O,Soulard L 2013 J.Appl.Phys.114 194902
[7]Zhang W Y,Ye W H,Wu J F,Miao W Y,Fan Z F,Wang L F,Gu J F,Dai Z S,Cao Z R,Xu X W,Yuan Y T,Kang D G,Li Y S,Yu X J,Liu C L,Xue C,Zheng W D,Wang M,Pei W B,Zhu S P,Jiang S E,Liu S Y,Ding Y K,He X S 2014 Sci.China:Phys.Mech.Astron.44 1(in Chinese)[张维岩,叶文华,吴俊峰,缪文勇,范征锋,王立锋,谷建法,戴振生,曹柱荣,徐小文,袁永腾,康洞国,李永升,郁晓瑾,刘长礼,薛创,郑无敌,王敏,裴文兵,朱少平,江少恩,刘慎业,丁永坤,贺贤土2014中国科学:物理学44 1]
[8]Zhang C Y,Hu H B,Li Q Z,Yuan S 2009 Chin.J.High Press.Phys.23 283(in Chinese)[张崇玉,胡海波,李庆忠,袁帅2009高压物理学报23 283]
[9]Weng J D,Tan H,Wang X,Ma Y,Hu S L,Wang X S 2006 Appl.Phys.Lett.89 111101
[10]La Lone B M,Marshall B R,Miller E K,Stevens G D,Turley W D,Veeser L R 2015 Rev.Sci.Instrum.86 023112
[11]Seifter A,Stewart S T,Furlanetto M R,Kennedy G B,Payton J R,Obst A W 2006 AIP Conf.Proc.845 239
[12]Seifter A,Grover M,Holtkamp D B,Payton J R,Rodriguez P,Turley D,Obst A W 2004 26th International Congress on High-Speed Photography and Photonics Alexandria,Virginia,September 19–24,2004 p93
[13]Ma Y,Wang X S,Li X Z,Zhang H Z,Hu S L,Li J B,Chen H,Wen J D 2006 Chin.J.High Press.Phys.20 207(in Chinese)[马云,汪小松,李欣竹,张汉钊,胡绍楼,李加波,陈宏,翁继东2006高压物理学报20 207]
[14]Asay J R 1978 J.Appl.Phys.49 6173
[15]Oró D M,Hammerberg J E,Buttler W T,MariamfG,Morris C,Rousculp C,Stone J B 2012 AIP Conf.Proc.1426 1351
[16]Rousculp C L,Oro D M,Morris C,Saunders A,Reass W,Griego J R,Turchi P J,Reinovsky R E https://www.osti.gov/scitech/biblio/1178310/[2015-4-20]
[17]Liu G R,Liu M B 2003 Smoothed Particle Hydrodynamics:A Meshfree Particle Methods(Singapore:World Scientific)pp309–339
[18]Wang P,Qin C S,Zhang S D,Liu C 2004 Chin.J.High Press.Phys.18 149(in Chinese)[王裴,秦承森,张树道,刘超2004高压物理学报18 149]
[19]Monfared S K,Buttler W T,Frayer D K,Grover M,LaLone B M,Stevens G D,Stone J B,Turley W D,Schauer M M 2015 J.Appl.Phys.117 223105
[20]Tan H 2007 Introduction to Experimental Shocked-Wave Physics(Beijing: National Defense Industry Press)pp36–43(in Chinese)[谭华 2007实验冲击波物理导引(北京:国防工业出版社)第36—43页]
[21]Zhang S Q,Liu C L,Li Q Z,Liu Q 2008 Acta Mech.Sin.40 535(in Chinese)[张世文,刘仓理,李庆忠,刘乔2008力学学报40 535]
[22]Sorenson D S,Pazuchanics P D,Johnson R P,Tunnell T W,Smalley D D,Malone R M,Kaufman M I,Marks D G,Capelle G A,Grover M,Stevens G D,LaLone B M,Marshall B F,Turley W D 2017 AIP Conf.Proc.1793 100026
[23]Buttler W T,Oró D M,Olson R T,ChernefJ,Hammerberg J E,Hixson R S,Monfared S K,Pack C L,Rigg P A,Stone J B,Terrones G 2014 J.Appl.Phys.116 103519
[24]Fung J,Harrison A K,Chitanvbs S,Margulies J 2013 Comput.Fluids 83 177
[25]Wang P,Sun H Q,Shao J L,Qin C S,Li X Z 2012 Acta Phys.Sin.61 234703(in Chinese)[王裴,孙海全,邵建立,秦承森,李欣竹2012物理学报61 234703]
[26]Igra O,Takayama K 1993 Proc.R.Soc.London 442 231
PACS∶47.15.Uv,62.50.Ef,47.11.—jDOI∶10.7498/aps.66.104701
*Project supported by the Science Challenge Project,China(Grant No.JCKY2016212A501).
†Corresponding author.E-mail:yy_stroller@163.com
Dynamical behaviors of Sn micro-sphere particles under shock wave action∗
Zhao Xin-Wen Li Xin-Zhu†Zhang Hang Wang Xue-Jun Song Ping Zhang Han-Zhao Kang Qiang Huang Jin Wu Qiang
(Laboratory for Shockwave and Detonation Physics,Institute of Fluid Physics,China Academy of Engineering Physics,Mianyang 621900,China)
11 November 2016;revised manuscript
28 February 2017)
In these decades,the turbulence mixing of micro-ejecta particles and gas has attracted considerable attention because it has great influence on inertial confinement fusion and some technologies of optical detection.It is significantly important for studying the evolution of micro-ejecta by investigating the influence of particle size and the transporting progress.In this paper,we experimentally investigate the micro-ejecta dynamical behaviors when a strong shockwave acts on Sn micro-sphere particles with different sizes of 0.1µm,1µm,5µm and 10µm.A strict experiment is carried out,in which a thin Tafl yer is accelerated by TNT explosion to load the Sn particles,and the velocity variation of ejecta particles transported in air is measured by the displacement interferometer system for any reflector.The results show that the tip-velocity of the micro-ejecta is very sensitive to the initial size of particle,where the larger size results in increased velocity.By analyzing the results of each case in detail,we discover that the formation of micro-ejecta is caused by the interaction between shockwave and the gap structure among several particles,where the larger gap structure induces faster ejecta tip-velocity.To verify this explanation,the effects of particle size on the ejecta tip-velocity is examined by simulating the cases of 5 µm and 10 µm in particle size through three-dimensional smooth particle hydrodynamics method.The simulated tip-velocity results are in good agreement with the corresponding experimental results.However,the scenario is different when the particle size is smaller than 1µm,where the experimentally measured tip-velocity of 0.1µm size particle is nearly the same as that of 1µm size particle.We attribute this to the fact that the gap structure is too small to affect the micro-ejecta progress and the micro-ejecta is mainly caused by the large scale defects accumulated by a huge number of particles.Furthermore,by comparing with the experimentally measured velocity decay,we also estimate the size distribution of ejecta particles by simulating the decelerating processes of different-sized particles with different initial velocities in gas.This paper is helpful in comprehending in depth the micro-ejecta process caused by the shockwave acting on micro particles,and also in designing such experiments accurately.
∶micron particles,micro-ejection,ejecta tip-velocity,particle transport
∗科学挑战专题(批准号:JCKY2016212A501)资助的课题.
†通信作者.E-mail:yy_stroller@163.com
©2017中国物理学会Chinese Physical Society
