一题多解案例剖析

■阙圣东

一题多解案例剖析

■阙圣东

很多几何问题，都有不同的解法，思维方式不同，得到的解法也各不相同。给学生这样一道题目，学生思维很开阔，提供了几种不同的解法，现将解法整理归纳，与同行交流。

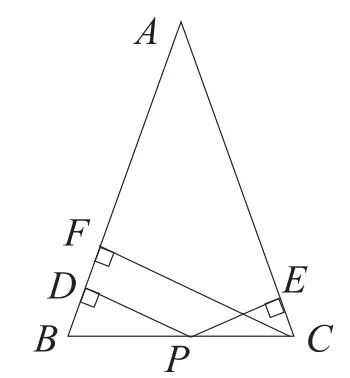
图1

一、原题呈现

如图，在△ABC中，AB=AC，P是底边BC上的一动点(不与点B、C重合)，过点P作PD⊥AB，PE⊥AC，垂足为D、E，CF是AB边上的高，求证：PD+PE=CF。

二、解法探究

解法1（作垂直，截长来转化）：过点P作PG⊥CF于点G。易证Rt△PGC≌Rt△CEP（AAS），因此CG=PE，所以CF=GF+CG=PD+PE。

解法2（作平行，截长来转化）：过D作DH∥BC交CF于点H。易证Rt△DFH≌Rt△CEP（AAS），因此HF=PE，所以CF=CH+HF=PD+PE。

解法3（作垂直，补短来转化）：过点C作CK⊥DP，交DP的延长线于点K。易证Rt△CKP≌Rt△CEP（AAS），因此PK=PE，所以CF=DK=PD+ PK=PD+PE。

解法4（巧割补，求面积得相等）：连接AP。由S△APB+S△APC=S△ABC，得AB·PD+AC·PE=· AB·CF，又因为AB=AC，即PD+PE=CF。

解法5（底角等，妙用三角函数）：在Rt△BDP中，PD=PB·sinB；在Rt△BFC中，CF=BC· sinB；在Rt△CEP中，PE=PC·sin∠ECP，又因为AB=AC，因此∠B=∠ECP，所以sinB=sin∠ECP，因为BC=PB+PC，即BC·sinB=PB·sinB+PC· sin∠ECP，所以CF=PD+PE。

解法6（得相似，用比例巧化归）：易证△BDP∽△BFC∽△CEP，因此利用比例的性质可得，即所以PD+PE=CF。

三、解题反思

这6种方法中的前三种解法是求证“一条线段等于另外两条线段和”问题的通法，截取较长的线段，或者延长较短的线段。解法4由高想到面积，即利用面积割补是众多解法中最特殊的解法，更是所有解法中最本质的解法。其本质就在于面积的转化，将大的三角形的面积转化为两个小的三角形的面积之和，回到数学最本质的根源。转化、化归都是一些基本的数学思想方法，除此之外，还有数形结合、分类、方程、模型思想等，数学思想蕴涵在数学知识形成、发展与应用中，因此，我们每一位教师在平时要精心设计教学活动，在教学环节中渗透数学思想，引导学生通过独立思考、合作交流，寻求到数学的本质，逐步感悟数学思想。

对于本题的不同解法，问题的切入点不同，则解法不同，解法5三角函数法从等腰三角形的两个底角思考，解法6比例化归由三个三角形都是相似三角形切入，解法不同，则思维方法不同，这就要求学生不断扩展思维能力，及时矫正解题中暴露的问题，弥补不足，巩固已有，而知识体系的构建可以帮助学生从不同角度思考解题方法，训练学生的发散思维，使得解题方法最优化。同时，变式练习可使学生在已有的数学基础知识与基础技能下，不断提高发现问题和提出问题、分析问题和解决问题的能力。

（作者为江苏省泰州市姜堰区张甸初级中学教师）