基于GA的车用锂离子电池电化学模型参数辨识*

徐 兴，王 位，陈 龙

(1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学汽车工程研究院，镇江 212013)



基于GA的车用锂离子电池电化学模型参数辨识*

徐 兴1,2，王 位1，陈 龙1,2

(1.江苏大学汽车与交通工程学院，镇江 212013； 2.江苏大学汽车工程研究院，镇江 212013)

本文中旨在对车用锂离子电池电化学模型进行参数辨识。首先在锂离子电池平均电极模型基础上，利用均匀离散的有限差分法简化电化学模型。基于对模型特性和参数类型的分析，运用遗传算法先后对固相锂离子扩散动力学参数和模型中剩余的参数进行辨识。最终通过多倍率放电实验和NEDC循环工况实验验证了算法的有效性和参数的准确性。结果表明，算法辨识的参数可保证模型输出精度，低倍率放电时单体电压偏差在±0.03V左右。

锂离子电池；电化学模型；遗传算法；参数辨识

前言

在对车用动力电池组进行控制和管理时，通常需要一个精确的电池模型来对电池状态做出准确的估计。等效电路模型凭借其结构简单、计算迅速的优点成为目前应用最为广泛的电池模型。常见的电池等效电路模型有经典的Rint[1]，RC[2]，Thevenin和PNGV[3]模型等。但电路模型利用电阻、电容等元器件模拟电池电压响应，对于前期的电池实验有很强的依赖性，模型的参数也不能对应电池内部实际的物理量，因此，在复杂的工况下电路模型无法达到足够的预测精度要求。电化学模型利用物理化学和电化学理论建立电池模型，它能反映电池内部反应机理，对电池内部的基本状态量作出准确预测，比如锂离子的浓度、电解液和固体电极材料中的电势等。但是，这类模型结构较为复杂，参数较多，很难直接应用。目前，国外对于电池电化学模型研究广泛，形成了许多成熟理论。例如，文献[4]中提出基于多孔电极理论的通用电池模型；文献[5]中提出电池微观与宏观特性相耦合的模型。另外，国外有大量基于电化学模型的电池状态估计和能量管理等问题的研究[6-7]。而国内的锂离子电池研究基本上是基于等效电路模型[8-10]，对于电化学模型研究较少[11]。本文中采用锂离子电池平均电极模型结合均匀离散的有限差分方法，一定程度上降低了电化学模型的复杂度，再利用遗传算法进行级联式参数辨识。最后通过多组不同倍率的电池放电实验对模型和参数辨识的准确性进行验证。

1 锂离子电池电化学模型

1.1 平均电极模型

文献[12]～文献[14]中提出了电池的平均电极模型，该模型是在文献[5]中提出的微观与宏观相耦合的电池模型基础上简化而来的。为降低模型的复杂度，将平均电极模型中电解液浓度被视为恒定的常值，且只考虑电池横截面上x轴方向的电极动力学特性。电池的结构原理如图1所示，图中电池被划分成正极、隔膜和负极3个区域，在电池充放电

过程中，锂离子在正负电极间往返嵌入和脱嵌。

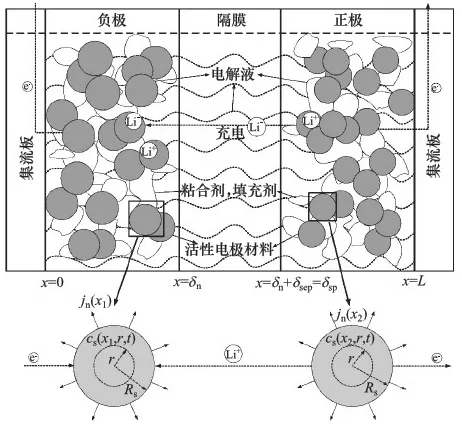
图1 锂离子电池结构原理图

电池电化学模型实际是由一系列描述电池内部电势和离子扩散的动力学方程组成，具体的方程和边界条件如表1所示[15]，由表中方程可构建一个理想的电池电化学模型，详细推导过程参见文献[12]，表中符号参见文献[15]。

表1 锂离子电池电化学模型方程组

平均电极模型以平均锂离子浓度取代了电极中锂离子浓度具体的分布情况，从而很大程度上降低了模型的复杂度。这样的假设类似于单颗粒模型SPM[15]，但相比之下该模型具有较高的阶次，且保留了电池固体颗粒中重要的扩散动力学特性。

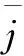
(8)

式中：I为负载电流；A为集流板面积；δ为电极区域厚度。

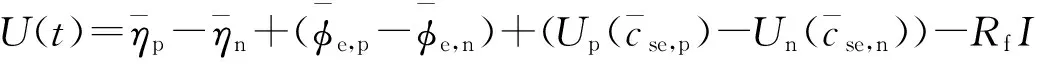
(9)

最终，电池的端电压可以表示为一个关于负载电流和电极固相平均锂离子浓度的函数，即

(10)

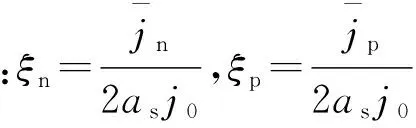
锂电池系统是一个强非线性分布式动力学系统，其系统状态耦合性较强，经过上述的简化后，模型可由式(5)和式(10)表示。而式(5)是偏微分方程，直接求解具有一定的难度，且最终建立的电池模型要应用于电池管理系统，式(5)就需要进一步简化。此外，从式(10)可以看出，要获得电池端电压也须先分析出电池固相锂离子浓度的分布情况。

1.2 固相锂离子扩散动力学

电极活性颗粒内锂离子的扩散运动是锂离子电池电化学模型中至关重要的动力学特性，式(5)固相扩散方程实质是球坐标表示的菲克第二定律。在颗粒半径方向作均匀离散再利用有限差分法可将该偏微分方程化简成一组常微分方程，即

(11)

结合相应的初始和边界条件，电极固相扩散方程可转化为一组状态空间方程，例如正极扩散方程的状态空间表示为

(12)

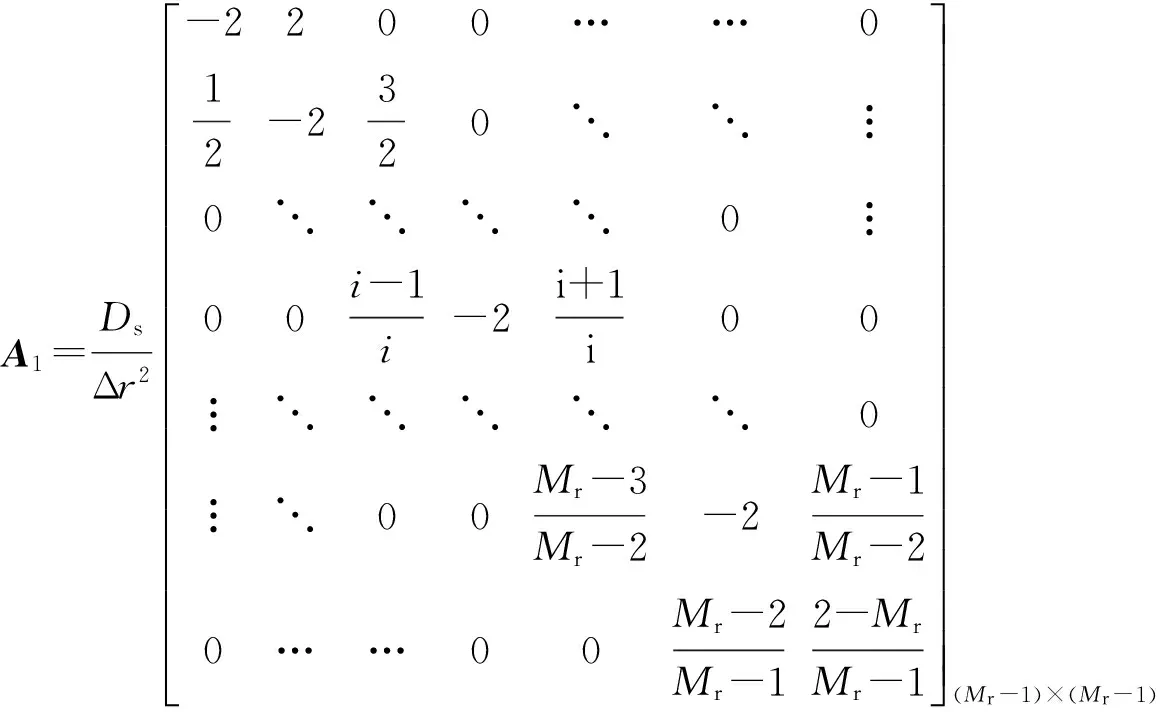
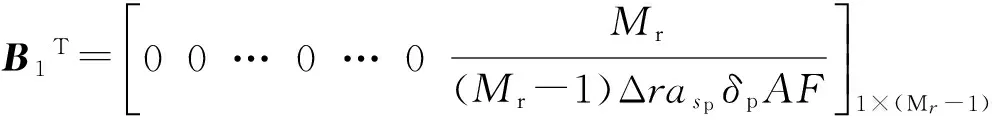
综合考虑简化后的扩散方程的精度和系统复杂度，在固相颗粒半径方向的均匀离散阶数取为100。至此，锂离子电池的平均电极模型就由正负极对应的固相锂离子扩散方程和一个端电压表达式构成。

1.3 电化学模型参数

电池的电化学模型可真实反映电池内部的电化学过程，模型涉及大量电池内部实际参数，如表2所示[16]，这些参数很难直接测得，参数的具体含义参见文献[15]。根据参数性质大致可以将它们分为性能、结构和恒定参数3大类，其中前两类参数对于不同电池单体会有所不同，也是下文中将要辨识的主要参数。

性能参数是决定电池充放电性能的主要因素，同类型的电池在不同的健康状态下性能参数有所不同，在将来的电池老化和健康问题的研究中可着重关注其中某些性能参数的变化。结构参数在电池的使用过程中不会有明显的变化，对于一致性较好的电池组，这些尺寸参数基本一致。

恒定参数包含了基本电化学系数、锂电池的恒定参数和一些容易获取的参数。其中θp,100，θn,100/θp,0，θn,04个参数分别表示在电池满电/空电状态下正负极固相锂离子浓度的状态，由于电池内部的浓度信息难以获取，此处参考了文献[12]中的取值。此外，受其影响的电池正负极开路电压分别是对应电极固相锂离子浓度状态的函数，且电极开路电压曲线大多是由实验数据拟合得到，上述的4个参数实质上只是限定固相锂离子浓度的状态量的变化区间，所以该参数的取值误差对于本文中的电池模型精度影响较小。

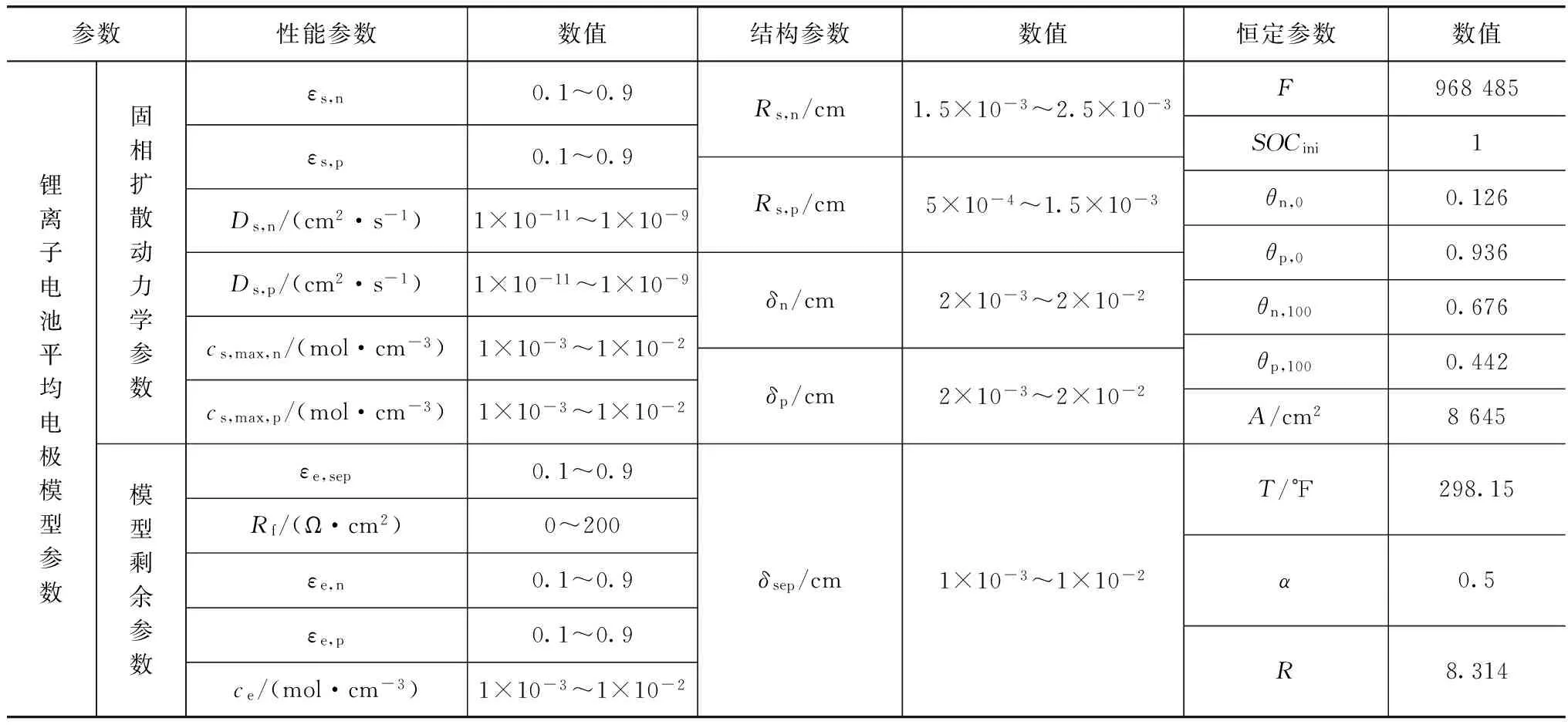
表2 锂离子电池电化学模型参数

电池在使用中必须严格避免电池发生过充过放的情况，在电化学模型中固相锂离子浓度与电池SOC密切相关。相应地，正负极固相锂离子浓度应该限定在上述参数范围内。下文中对电池模型固相锂离子扩散动力学部分单独进行了参数辨识，以有利于保证仿真中电池处于正常的运行状态和缓解一次性参数辨识带来的工作量大，精度较低和算法复杂等问题。

2 遗传算法参数辨识

2.1 遗传算法

遗传算法[17]是一种以自然选择和遗传理论为基础的高效全局寻优搜索算法。算法中的每一个由符号串表示的个体都代表着问题的一组可能解，由预定目标适应度函数可求得群体中所有个体的适应度值，再依据适者生存、优胜劣汰的进化规则，对群体反复进行遗传、交叉、变异和重组，不断得到更优的群体，同时以全局并行搜索方式来搜索优化群体中的最优个体，最终求得满足要求的最优解。具体算法步骤如下。

第1步：参数设置

根据电池模型确定算法的一些基本参数，包括个体数量、遗传代数和变量维数等。

第2步：设置区域描述器

根据表2中给定的电池参数范围，建立区域描述器，限定算法中参数变量的取值范围。

第3步：产生初始种群并计算个体的适应度

算法中用一串二进制数代表一组完整的模型参数，即一组解，多个字符串构成一个种群。设定目标函数计算出每组参数对应的误差，可相应得到每组参数的适应度。

第4步：选择

根据上一步计算出的适应度值来选取误差较小的参数解并保留下来，采用了随机遍历抽样，模拟自然进化的优胜劣汰原则。

第5步：交叉

算法通过染色体交叉产生新的个体，又称基因重组。本文中采用单点交叉方式，保证产生新的一组参数解具有较高的适应度。

第6步：变异

变异函数同样是模拟自然进化中染色体的随机变异过程，即染色体上某个基因发生突变，变异也是新个体产生的一种方式。变异概率取值为0.7/染色体长度。

第7步：个体重组产生下一代种群

通过交叉变异产生新的个体与上一代种群结合，进行选取重组，构成新一代种群并计算适应度搜索最优解。

第8步：循环迭代至算法终止

重复上面的第4～7步直至达到预先设定的遗传代数或最优个体的某个性能指标。

所研究的电化学模型较为复杂，涉及的电池参数较多，遗传算法正适用于解决此类问题。根据1.3节电化学模型参数的模型结构和参数划分情况，可将全部参数分为两部分依次辨识。

2.2 固相锂离子扩散动力学相关参数辨识

正负电极的固相锂离子扩散动力学在模型中扮演着相对独立而又至关重要的角色，通过求解扩散方程可获取固相锂离子的浓度变化信息。在模型参数辨识中首先对该部分涉及的参数进行辨识求解。由式(12)状态空间方程，可建立正极电极的固相锂离子扩散动力学模型，如图2所示。

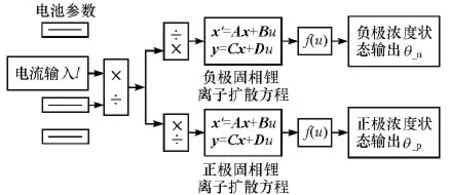
图2 固相锂离子扩散动力学模型

根据上述的算法步骤编写参数辨识代码，取定算法中个体数量nind=50，遗传代数maxgen=50，变量维数nvar=10，变量的二进制位数preci=9，遗传代沟ggap=1，交叉率和变异率分别为0.7和0.008。

算法中个体的评价指标为放电终了正负极固相锂离子浓度的误差函数，表达式为

error(i)=abs(θ_n-θn,0)+abs(θ_p-θp,0)

(13)

式中：θ_p和θ_n分别表示正负电极在放电终了时固相锂离子浓度状态，该目标函数一方面可作为个体适应度的计算指标，另一方面也避免了仿真中电池产生过放的危险状态。

算法运行结果如图3所示，各代种群的平均误差和各代最优个体的误差都随着遗传代数的增长逐渐降低收敛，第50代最优个体的误差值为0.005 4，误差可以接受。最终辨识的电池参数如表3所示。

2.3 正负电极开路电压曲线拟合

平均电极模型将电池端电压分为4个部分，分别为过电势、电解液相电势、电极开路电势和内阻引起的电势。式(9)中的第3项为电池正负电极开路电势差，电极的开路电势通常表示为电极固相锂离子浓度状态的函数，可由实验数据拟合得到。不同材料的电极开路电势各不相同，本文中研究的电池为三元锂电池，负极材料为LixC6，正极材料为Li(NiCoMn)O2，电池容量为5.3A·h。目前，电池负极材料基本相差不大，而正极材料种类较多，相应的开路电势变化曲线也各不相同。因此，本文中的负极开路电势表达式引用了文献[7]中的多项式，而正极材料的开路电势表达式则通过多项式拟合实验数据获得：

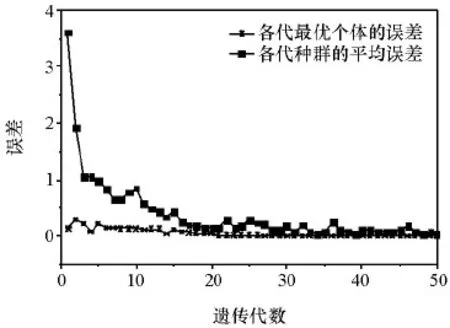
图3 经过50次迭代后的最优解和性能跟踪

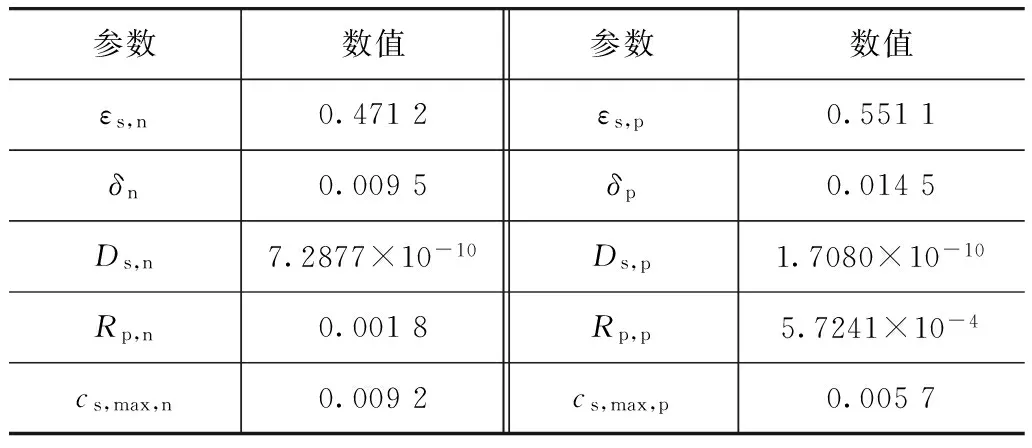
参数数值参数数值εs,n0.4712εs,p0.5511δn0.0095δp0.0145Ds,n7.2877×10-10Ds,p1.7080×10-10Rp,n0.0018Rp,p5.7241×10-4cs,max,n0.0092cs,max,p0.0057

U-(θn)= 0.7222+0.1387θn+0.029θn0.5-0.0172/θn+

0.0019θn-1.5+0.2808exp(0.9-15θn)-

0.7984exp(0.4465θn-0.4108)

(14)

U+(θp)= -3336608θp10+2224336θp9-66321816θp8+

116462170θp7-133373853θp6+

104078116θp5-56042493θp4+20560010θp3-

4917875θp2+692535θp-43591.6828

(15)

式中：U+和U-分别为正负极开路电势；θp和θn分别为正负电极的锂离子浓度状态。

电势与浓度状态的关系曲线如图4和图5所示。

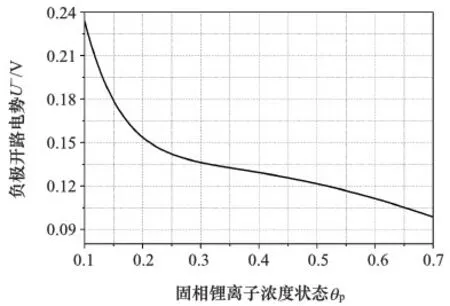
图4 负极开路电势变化曲线

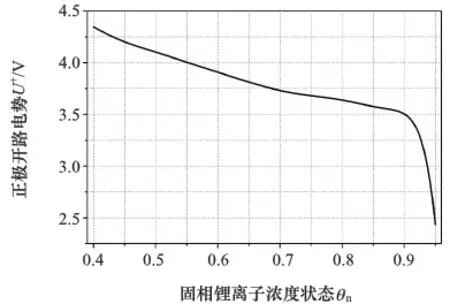
图5 正极开路电势变化曲线

2.4 模型剩余参数辨识

模型剩余参数同样可利用遗传算法辨识获得。在已辨识的固相扩散动力学相关参数的基础上，利用式(10)和式(12)建立完整的电池平均电极模型，如图6所示。

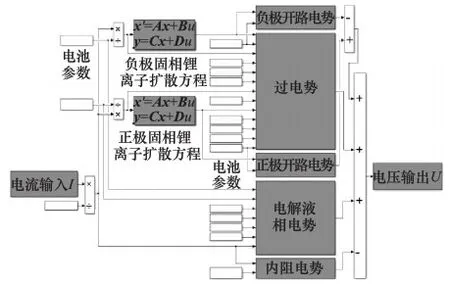
图6 锂离子电池平均电极模型

模型输入为负载电流，输出为电池端电压，结合电池实验数据编写参数辨识代码，最终可获得全部电池参数。遗传算法中个体数量nind=40，遗传代数maxgen=10，变量维数nvar=6，其他参数设置与前面相同。

算法中个体的评价指标为电池端电压的平均误差函数：

error(i)=avg(Usim-Uexp)

(16)

式中：Usim和Uexp分别为电池端电压的模型仿真值和实验测量值。

算法运行结果如图7所示，第10代最优个体的误差值为0.003 0，可以接受。剩余6个参数的辨识结果如表4所示。

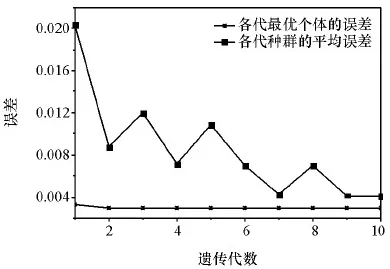
图7 经过10次迭代后的最优解和性能跟踪

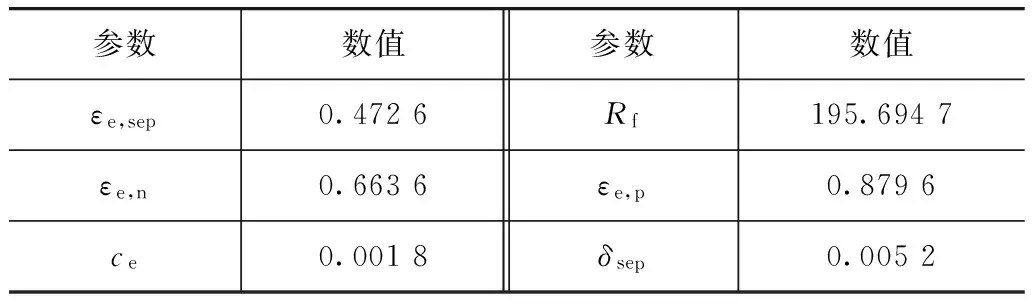
参数数值参数数值εe,sep0.4726Rf195.6947εe,n0.6636εe,p0.8796ce0.0018δsep0.0052

至此，平均电极模型的16个未知参数经过两次遗传算法辨识已全部获得，参数误差控制在合理的范围之内。参数辨识中使用的电池测试为0.2C恒温恒流放电至截止电压2.7V后静置15min，初始SOC为100%，环境温度为25℃。图8为电池电压实际测量值与模型输出值的对比。由图看出，仿真中模型输出的电池端电压与实验数据基本保持较高的一致性，只在放电终了和静置阶段存在细微误差，说明遗传算法辨识的模型参数能够满足电池模型的精度要求。

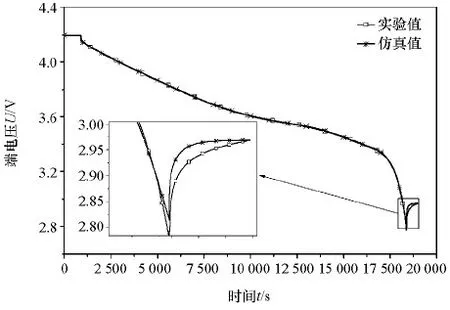
图8 0.2C电池放电下实验与仿真结果对比

3 仿真与实验

基于电池0.2C放电实验完成了电池电化学模型所有参数的辨识，最终模型的电压输出与实验值基本一致。为检验参数的准确性和模型的有效性，利用如图9所示的新威电池测试系统进行不同倍率下的电池放电实验。实验包含了0.2C，0.5C，1C，1.5C和2C 5种不同倍率下的电池恒流放电实验。电池的初始SOC为100%，环境温度保持在25℃，在达到2.7V截止电压时终止放电并静置15min，结果如图10所示。

图9 新威电池测试系统

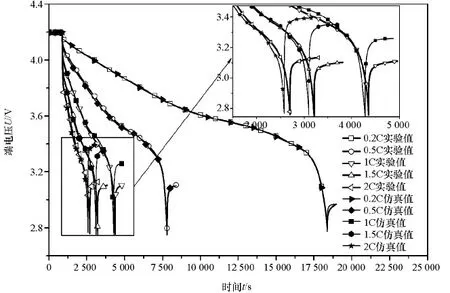
图10 电池放电的实验与仿真对比

由图10可见，总体上，随着电流增大，模型的输出电压误差增大，由1C，1.5C和2C放电曲线可以看出，误差主要集中在放电终了及其结束后的静置过程中。且在有充放电截止电压保护的恒流充放电过程中，电流越大对应的充入或放出的电量越小，图10可以很好地反映这一特性，但在实际测试中，3组实验对应的放电容量十分接近，导致了图中1C，1.5C和2C的仿真曲线存在明显的“滞后”现象。此外，电池电压与SOC相关，由于放电容量十分接近，相应地，在放电终了3组实验电池的SOC也很接近，所以在静置过程中这3组电池的最终电压基本一致。而仿真中1C，1.5C和2C 3组的放电容量依次减小，最终静置的电压也依次增大，与实验值误差明显。放电阶段3组实验的电压平均误差分别为0.015 6，0.014 6和0.021 6V，最大偏差不超过0.1V。最终的静置电压偏差分别为0.149，0.248和0.26V。

为进一步研究该参数辨识方法所获得的模型参数在实际工况下的有效性，利用底盘测功机进行了微型纯电动汽车的NEDC城市循环工况实验，实验平台如图11所示。该实验中，给底盘测功机转鼓上的两前轮轮毂电机控制器发出一定的控制信号来驱动样车，并通过CAN采集电池管理系统BMS中电池单体的电压、电流和温度等信号。实验样车设计最高车速为96km/h，因此在高速工况下样车只能保持最高车速行驶，具体如图12所示。该实验样车还搭载了制动能量回收系统，在运行中电池处于持续充放电状态，电池初始SOC为100%，实验终了SOC为93%。

图11 底盘测功机道路模拟实验

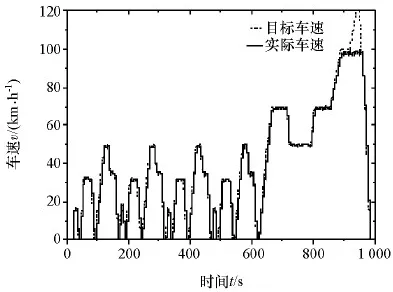
图12 NEDC循环工况

实验样车电池包内的电池先由24个单体电池并联构成电池组，再由40个电池组串联构成电池包，电池包额定电压为160V，额定容量为127A·h。其中单体电压可直接采得，单体电流可通过采集母线电流再除以24计算得到。最终NEDC工况下的电池实验结果如图13所示。由电流曲线可以看出，在城市低速工况下电池基本处于0.5C左右的小电流充放电，在加速阶段以及高速工况下放电倍率可达1C至1.5C。对比模型输出电压和实际BMS中采集的单体电压可以发现，两者总体的变化趋势一致，在低速工况下模型输出电压基本贴近实际值，误差总体在±0.03V左右；在高速工况误差较大，基本在±0.08V左右，最大误差可达0.2V。电压误差的构成主要有两方面，一方面是传感器测量精度低造成的测量误差；另一方面是本文中提出的该电池电化学模型自身的模型误差，在大电流充放电时的模型精度有待提高。此外，电池的充放电效率、温度和容量衰减等问题都会造成仿真输出与实际值之间存在一定偏差，这些都值得深入研究。

4 结论

通过对锂离子电池内部电极动力学的分析，利用电化学理论建立了电池的电化学模型。电池的电化学模型是一个多回路强非线性系统，借鉴文献[12]～文献[14]中的平均电极思想，再结合均匀离散的有限差分法，最终获得简化的平均电极模型。通过对模型参数特性的分析和分类，结合遗传算法，在0.2C的电池放电实验的基础上经过两次辨识获得了模型的全部参数，参数误差在合理范围之内。由0.2C～2C多倍率电池放电实验可知，由遗传算法辨识的模型参数总体上能够保证电池模型精度，放电阶段电压最大误差均在0.1V以内，只是在大电流放电末期，模型与实际电池电压存在一定偏差。

最终通过底盘测功机进行了微型纯电动汽车的NEDC城市循环工况实验，对比电池实际电压与模型输出电压，可以得出提出的该参数辨识方法能够保证电池模型在1C以内低倍率充放电时具有较高精度，误差基本在±0.03V左右，对于基于电化学模型的电池管理系统的研究具有实际价值。

为促进电池电化学模型在车用动力电池管理系统中的应用，提出的平均电极模型的完善以及模型的简化，不同工况下的输出特性等问题是接下来研究的重点。

[1] 徐梁飞,李建秋,杨福源,等.燃料电池混合动力系统镍氢电池特性[J].清华大学学报(自然科学版),2008,48(5):864-867.

[2] 魏学哲,孙泽昌,田佳卿.锂离子动力电池参数辨识与状态估计[J].同济大学学报(自然科学版),2008,36(2):231-235.

[3] 张彩萍,姜久春.用基于遗传优化的扩展卡尔曼滤波算法辨识电池模型参数[J].吉林大学学报(工学版),2012,42(3):732-737.

[4] DOYLE M, FULLER T F, NEWMAN J. Modeling of galvanostatic charge and discharge of the Lithium/polymer/insertion cell[J]. Journal of Electrochemical Society,1993,140(6):1526-1533.

[5] WANG C Y, GU W B, LIAW B Y. Micro-macroscopic coupled modeling of batteries and fuel cells. Part I: model development[J]. Journal of Electrochemical Society,1998,145(10):3407-3417.

[6] BARBARISI O, VASCA F, GLIELMO L. State of charge Kalman filter estimator for automotive batteries[J]. Control Eng. Pract.,2006,14(3):267-275.

[7] SANTHANAGOPALAN S, WHITE R E. Online estimation of the state of charge of a Lithium ion cell[J]. Ecs Transaction,1985,19(1):57-58.

[8] 刘光明,欧阳明高,卢兰光.基于电池能量状态估计和车辆能耗预测的电动汽车续驶里程估计方法研究[J].汽车工程,2014,36(11):1301-1309.

[9] 杨世春,麻翠娟.基于PNGV改进模型的SOC估计算法[J].汽车工程,2015,37(5):582-598.

[10] 毕军,康燕琼,邵塞.纯电动汽车动力锂电池Nernst模型参数辨识[J].汽车工程,2015,37(6):725-730.

[11] 张立军,李文博,程洪正.设计不均匀发热与温度分布的锂离子电池电化学-热力学耦合三维有限元模型[J].汽车工程,2015,37(12):1382-1389.

[12] DI DOMENICO D, STEFANOPOULOU A, FIENGO G. Lithium-ion battery state of charge and critical surface charge estimation using an electrochemical model-based extended Kalman filter[J]. Journal of Dynamic Systems, Measurement and Control,2010,132(6):768-778.

[13] DI DOMENICO D, FIENGO G, STEFANOPOULOU A. Lithium-ion battery state of charge estimation with a Kalman filter based on a electrochemical model[J]. IEEE International Conference on Control Applications,2008,1:702-707.

[14] DI DOMENICO D, STEFANOPOULOU A, FIENGO G. Reduced order Lithium-ion battery electrochemical model and extended Kalman filter state of charge estimation[J]. ASME Journal of Dynamic Systems, Measurement and Control-Special Issue on Physical System Modeling,2010.

[15] XU X, WANG W, CHEN L. Order reduction of Lithium-ion battery model based on solid state diffusion dynamics via large scale systems theory[J]. Journal of Electrochemical Society,2016,163(7):1429-1441.

[16] CHATURVEDI N A, KLEIN R, CHRISTENSEN J, et al. Algorithms for advanced battery management systems[J]. IEEE Control System,2010,30(3):49-68.

[17] 雷英杰,张善文,等.MATLAB遗传算法工具箱及其应用[M].西安:西安电子科技大学出版社,2005.

Parameter Identification of Electrochemical Model for VehicularLithium Ion Battery Based on Genetic Algorithm

Xu Xing1,2, Wang Wei1& Chen Long1,2

1.SchoolofAutomotiveandTrafficEngineering,JiangsuUniversity,Zhenjiang212013；2.AutomotiveEngineeringResearchInstitute,JiangsuUniversity,Zhenjiang212013

This paper aims to conduct parameters identification of the electrochemical model for vehicular lithium-ion battery. Firstly on the basis of electrode averaged model for lithium-ion battery, its electrochemical model is simplified by using even discrete finite difference method. Then based on the analyses on model characteristics and parameter types, the solid state diffusion kinetics parameters of lithium-ion and the remainder parameters in the model are identified successively with genetic algorithm (GA). Finally the discharge experiments with different current rates and NEDC cycle tests validate the effectiveness of algorithm and the correctness of parameters. The results show that the parameters identified with GA ensure the accuracy of model output, with an error of single battery voltage is only around ±0.03V in low-rate discharge.

lithium ion battery; electrochemical model; genetic algorithm; parameter identification

10.19562/j.chinasae.qcgc.2017.07.014

*江苏省“六大人才高峰”项目(2014-JXQC-004)和中国博士后科学基金(2015M571680)资助。

徐兴，副教授，E-mail:xuxing@mail.ujs.edu。

原稿收到日期为2016年5月10日，修改稿收到日期为2016年9月26日。