粒子群优化的稀疏分解在雷达目标识别中的应用

赵东波，李 辉

（1.西安航空学院 电子工程学院，陕西 西安 710077；2.西北工业大学 电子信息学院，陕西 西安710129）

粒子群优化的稀疏分解在雷达目标识别中的应用

赵东波1，李 辉2

（1.西安航空学院 电子工程学院，陕西 西安 710077；2.西北工业大学 电子信息学院，陕西 西安710129）

基于稀疏分解的方法把雷达高分辨距离像（HRRP）表示在一个超完备Gabor时频字典上，进而提取字典原子的特征参数作为特征向量进行识别；针对匹配追踪算法计算量大的问题，利用粒子群算法搜索能力强收敛速度快的优点对OMP算法进行改进。通过对雷达高分辨距离像（HRRP）的识别实验表明，采用Gabor原子提取的特征参数作为特征向量对雷达目标的分类效果比较好，同时，基于粒子群算法改进的OMP大大降低了参数寻优的计算量。

高分辨率距离像（HRRP）；匹配追踪；Gabor原子；粒子群算法（PSO）；特征提取

特征提取是雷达目标分类识别中一个重要的环节，它决定着最终的识别效果。目前就高分辨距离像（HRRP）在雷达目标识别中的应用有很多方法，但无论哪种方法必须面对的问题是高分辨距离像中包含了目标很多特征信息，获取这信息数据量很大，因此需要对HRRP稀疏分解后再进行特征信息的获取。所以提出了通过稀疏表示的方法在一个超完备时频字典上把信号展开后再分析，这样就可以从具有时频结构的信号中提取出目标的特征信息[2]。

匹配追踪（MP）算法以及在其基础上改进的正交匹配追踪（OMP）算法在稀疏表示（Sparse Representation，SR）方法中最简单但应用广泛。匹配追踪算法是依据信号特点构成超完备原子库，然后从中搜索与信号最接近的原子。其中超完备原子库的Gabor原子具有很好的时频特性，所以利用Gabor字典分解信号，能更清楚地反映出信号的时频特性。但存在的问题是，普通的OMP稀疏算法的原子参数寻优过程计算量太大。因此，本文利用稀疏分解的方法通过具有最小时频积的Gabor原子对雷达回波信号进行稀疏分解，并基于粒子群算法（PSO）对OMP算法改进来解决其参数寻优过程计算量过大的问题。

1 稀疏分解算法

1.1 匹配追踪算法（MP）算法

稀疏表示实质是用训练样本构成的过完备字原子将原始信号表示为这些原子的线性组合，目的是使重建信号逐步逼近原始信号，在具体的算法中利用残差值的迭代收敛来实现对原始信号的逼近。匹配追踪算法 （MP）在每次迭代中都会从完备原子库中选择最匹配的原子来逼近信号的局部时频结构，是一种自适应信号稀疏迭代算法。但MP算法在每次迭代运算中使新的残差与前次确定的原子正交，即〈rt，θj〉=0，但在已选定原子所构成的子空间上的原子间并不是正交的，信号对子空间的投影不是正交投影，这就使得重构信号不够精确，影响了其误差的收敛速度。

1.2 正交匹配追踪算法（OMP）算法

针对对MP算法进行改进，OMP算法在残差迭代过程中加入施密特正交化，这样就保证了信号残差与已选定的所有原子都正交。在由正交的原子组成的新空间中对信号投影，就可以得到已选定原子的系数和信号残差，对信号残差使用相同的处理从而得到稀疏系数，最终得到N个正交原子线性表示的原始信号。在投影的过程中信号残差下降的很快，因此可以用更少的原子来表示原始信号。

OMP算法的步骤如下[2]：

1）第一步要从过完备原子库中选择与原始信号f最匹配的原子gk1，其须满足：

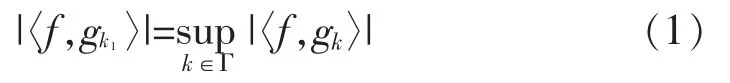
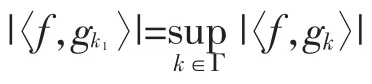
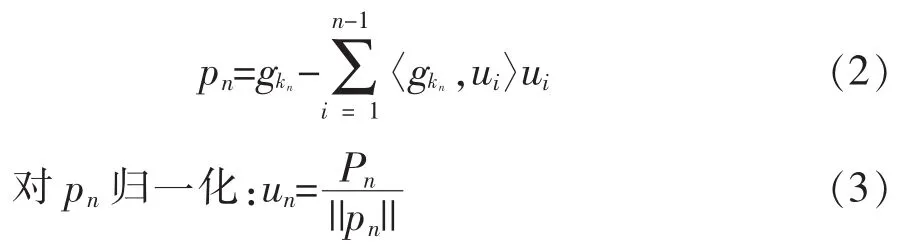
3）将每一步的残差信号投影到上，可得到：

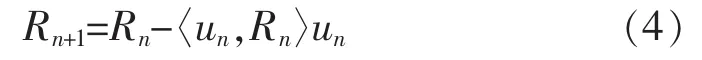
4）当进行到第N步，迭代误差满足||RN||2≤ε2||f||2时停止。

5）原信号可表示为：

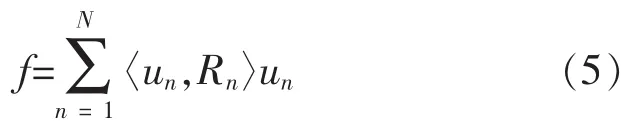
由于OMP算法在分解过程中的每次迭代选所有选定的原子都进行正交化，所以OMP算法的收敛速度要快于MP算法，在相同稀疏精度下所需的原子数量要少于MP算法。

2 基于Gabor字典的特征提取

2.1 Gabor字典

由 Gabor原子构成的过完备集合称为Gabor字典，Gabor具有很好的时频特性，所以利用Gabor字典分解信号能较好地表达信号的时频特性。Gabor字典是由经过伸缩、位移、频率调制的高斯函数组成的原子集合，其数学表达式为[5]：

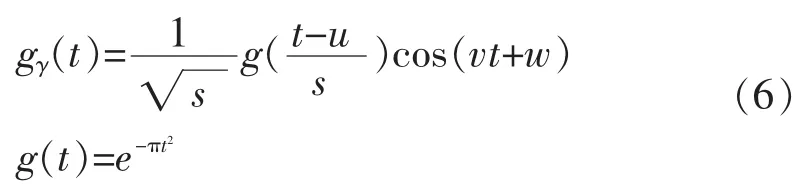
其中，g（t）为高斯窗函，γ=（s，u，v，w）作为时频参数分别代表幅度、位移、频率、相位。Gabor参数按照文献[5]的方法进行如式离散化采样：

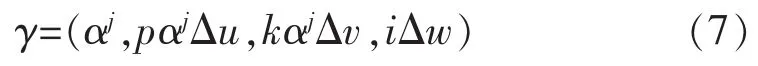
其中参数的取值范围为：α=2；0≤p≤N·2-j+1；Δu=1/2；0≤k≤2j+1；Δu=π；0≤i≤12；Δw=π/6；0＜j≤1bN；N为信号长度。这样，由这些离散的时频参数就可以构造Gabor字典了。

2.2 基于Gabor字典特征提取

由 Gabor字典的构造可知：g（t）=e-πt2是高斯窗函数，γ=（s，u，v，w）是时频参数。并且时频分布的 Gabor原子仅仅是进行了时移和频谱变化，其分布是保持不变得，也就是说Gabor原子具有时移、频移不变性。

雷达高分辨率距离像（HRRP）所具有的平移敏感性对目标分类是不利的，而时频的分布是平移不变的。因此，可以利用稀疏表示算法将雷达回波信号在具有时频特性的Gabor字典上投影，把每次迭代产生相对应的特征参数作为特征向量来进行分类，就可以克服平移敏感性这一不利影响。

3 改进的OMP算法

要实现以上介绍的基于Gabor字典特征提取主要是在稀疏分解时使用过完备原子库，OMP算法就是持续从这个过完备原子库中寻找最逼近原始信号及其残差信号的时频原子并追踪匹配后的残差，其每一次匹配追踪均需要把信号或信号分解的残差与过完备库中每一个原子做高维的内积运算以实现一个多参数优化问题，这样必然会造成信号稀疏分解数次匹配的计算量很大。针对此问题，提出了一种基于粒子群算法（PSO）改进的OMP算法。

3.1 粒子群算法（PSO）

粒子群算法是一种是基于群体智能理论的优化算法。因为有很好的寻优能力，PSO广泛应用于求解各种非线性不可微的复杂优化问题，如函数优化、数据挖掘、人工神经网络训练等领域。

在粒子群算法中，每一个优化问题的解被看作搜索空间的粒子。

1）算法开始时首先生成初始解，即在可行解空间中随机初始化m粒子组成的种群Z={Z1，Z2，…，Zm}，其中每个粒子所处的位置Zi={zi1，zi2，…zim}都表示问题的一个解，并且根据目标函数计算每个粒子的适应度值。

2）然后每个粒子都将在解空间中迭代搜索，通过不断地调整自己的位置来搜索新解。在每一次迭代中，粒子将跟踪两个“极值”来更新自己，一个是粒子本身搜索到的最好解pid，一个是整个种群目前搜素到的最优解pgd这个极值即全局极值。

3）并且每个粒子都有个速度 vid={vi1，vi2，…，vin}，但两个最优解都找到后，每个粒子根据下式来更新自己的速度：

其中，vid（t+1）表示第i个粒子在 t+1次迭代中第d维上的速度；w表示惯性权重，η1，η2为加速常数，rand（）为0～1之间的随机数。同时，为了避免粒子速度过大而设置速度上限，即当 vid（t+1）＞vmax时vid（t+1）=vmax；vid（t+1）＜-vmax时 vid（t+1）=-vmax。

4）当达到算法的结束条件时，即找到足够的最优解或达到最大迭代次数时，算法结束。

3.2 利用粒子群优化实现快速稀疏分解

Gabor字典的冗余度很高，搜索算法是求内积最大，内积运算计算量就很大了，OMP算法要遍历内积字典因此计算量非常大[7]。而采用粒子群算法搜索最优原子时，只需要搜索少量的参数空间点（迭代次数*种群数量），再有这些参数空间点构成原子[9]。相对于内积运算，PSO算法粒子速度和位置的更新运算量就很小了[9]，所以可以很快收敛，得到最佳匹配原子。

利用粒子群优化搜素最佳匹配原子并实现快速稀疏分解的算法流程如图1所示。

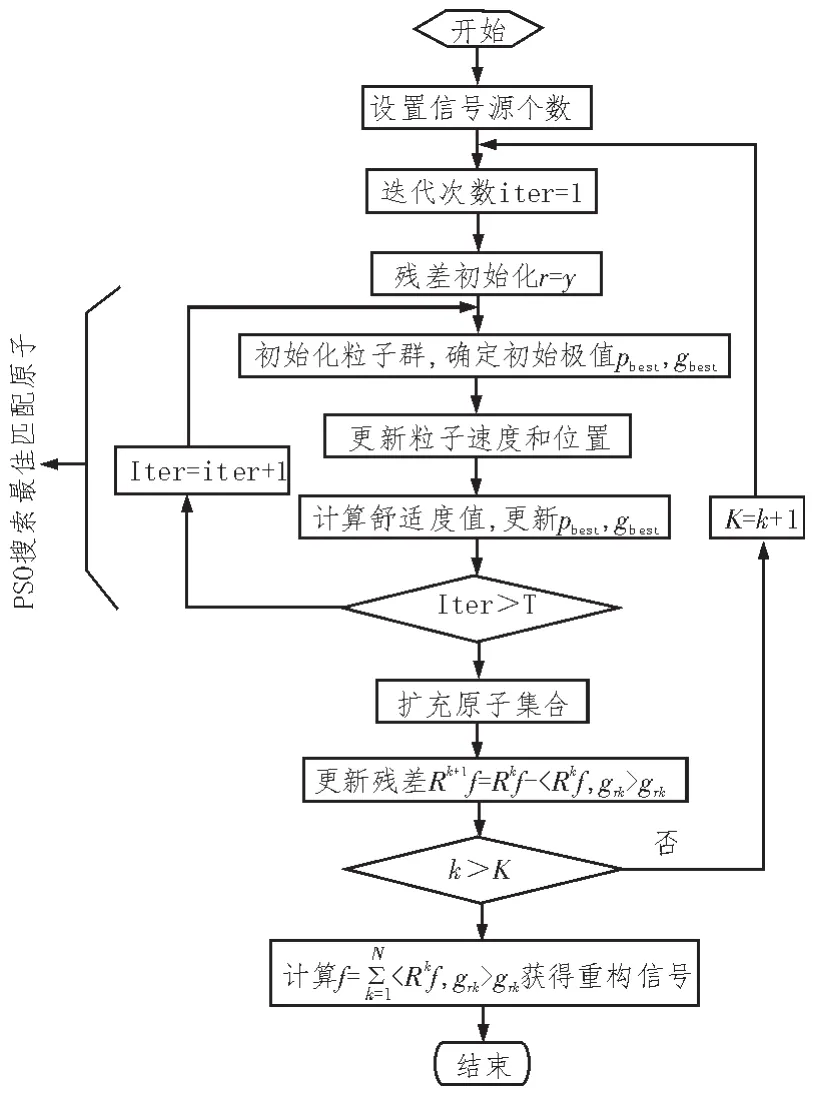
图1 基于粒子群优化的稀疏分解算法流程图

1）定义每个原子就是一个粒子，粒子位置就是原子参数 γ=（s，u，v，w）所表示的 4 维向量。 粒子的适应度函数为：

2）初始化粒子群，并根据初始粒子适应度寻找个体极值Pbest和全局极值gbest。

3）根据公式（6）和（7）更新粒子的飞行速度和位置。同时检查粒子的位置是否在范围内，如果否则取边界值代替粒子的位置。判断粒子的飞行速度是否超出界限，否则不更新。

4）更新粒子的个体最优极值和全局极值。计算每个粒子的适应度值，如果大于个体极值pbest，则把pbest替换为当前位置，否则保持不变；如果有粒子中个体极值pbest优于gbest，则重新设置gbest为当前粒子的位置，否则保持不变。

5）满足迭代次数则终止，并输出全局最优解即最佳匹配原子的参数，进一步计算得到最佳匹配原子。否则返回步骤3）继续搜索最佳匹配原子。

6）利用公式（11）更新信号或者信号残差，

7）重复多次进行上述过程，就可以实现信号的稀疏分解。

4 仿真实验

4.1 实验数据

文中实验采用3种飞机（安-26、奖状、雅克42）的仿真数据，信号长度为400。雷达发射脉冲的带宽为400 MHz（距离分辨率为1 m，雷达径向采样间隔为0.5 m）。选取目标的俯仰角有一定差异的数据作测试数据。由参数所构造的Gabor字典重构雷达移位高分辨率距离像（HRRP）。粒子群优化的种群规模设定为50个粒子，迭代次数为30，最大速vmax=（vs，vu，vv，vw）=（150，150，10，10），γ =（αj，pαjΔu，kαjΔv，iΔw），ωmax=0.9，ωmin=0.1，c1=c2=2.1。

4.2 稀疏分解的仿真实验

首先，利用 MP、OMP算法对 HRRP数据在Gabor字典上进行稀疏分解，对每个目标的每个角度数据经过60次迭代得到相应的Gabor参数。每次迭代的参量组合起来作为特征，并使用支持向量机（SVM）作为分类器进行目标识别。

表1 OMP算法对HRRP数据在Gabor字典上进行稀疏分解提取到的Gabor参数（部分）

表2 两种不同算法提取的Gabor特征参数利用SVM分类器识别的识别率

由表2的统计结果可知，使用支持向量机（SVM）分类器对两类目标仿真数据所得到的Gabor字典特征参数进行识别，平均识别率在87%以上，所以该方法可以实现对雷达高分辨率距离像（HRRP）有效的识别。

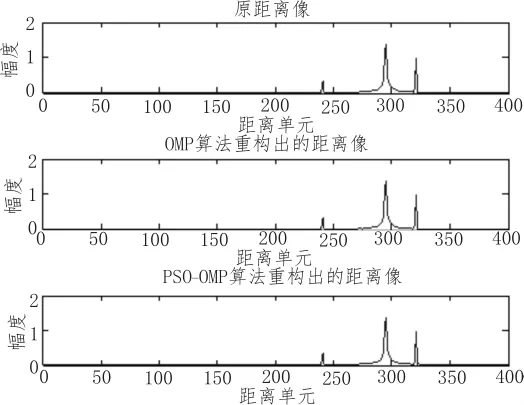
图2 各算法的信号重构图

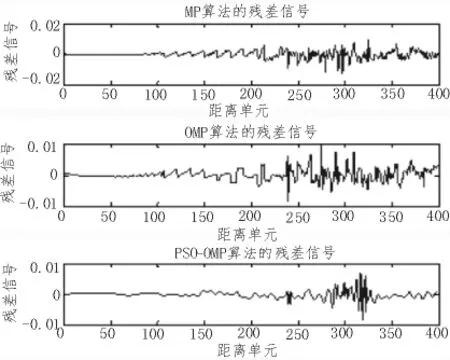
图3 是各算法的残差信号图

图2中给出了利用OMP和基于PSO改进的OMP两种算法对雷达目标距离像稀疏分解为30个原子后重建的信号。通过稀疏重构波形分析，OMP及改进的PSO算法均能实现雷达高分辨率距离像信号的稀疏重构，并且3种稀疏算法重构出的波形相差不大，都有很好的效果。

图3是各算法的残差信号图，通过对各算法的误差波形分析可知，PSO-OMP算法下的误差波形幅值较MP、OMP相对比较平稳，具有更小的能量残差，因此匹配信号特征更加精确，具有良好的信号表达稀疏精度。

接着，通过仿真实验来比较基于粒子群算法优化的PSO-OMP算法与OMP算法在改善在参数寻优中收敛速度上的差别。

图4是对MP、OMP和PSO-OMPS 3种算法的收敛性比较，通过对两种算法收敛性的比较分析可知，PSO-OMP收敛最快、效率最高。由于引入了寻优机制，相较于OMP算法[16-17]，PSO-OMP可以有效地提高OMP过程中遗传算法搜索最佳原子的收敛速度并降低其计算量。收敛速度不同导致稀疏分解运算时间上也会有差异。以MP算法的分解速度为基准，PSO-OMP算法的稀疏分解速度将提高19倍。

图4 OMP和GAOMP算法的收敛性比较

表3 不同稀疏分解算法相对速度的比较

表3中给出基于OMP的信号稀疏分解算法和本文算法的重建信号误差以及运行相对速度比较，可以看出来利用基于PSO改进的OMP算法对采样样本数据在Gabor字典上进行稀疏分解得到相应的Gabor参数的相对速度要远远大于OMP算法的速度。

5 结束语

通过稀疏分解方法将雷达高分辨距离像（HRRP）展开在一个超完备Gabor时频字典上,把具有局部化时频结构的Gabor参数作为特征量然后再利用SVM分类器进行了识别，实验表明了这种特征提取的方法是可行的并且有比较好的效果。同时，通过实验仿真分析表明采用基于粒子群算法（PSO）改进的OMP算法很好地解决了匹配追踪算法中的计算量大的问题，使信号稀疏分解的速度大大提高。

[1]史峰，王辉.MATLAB智能算法案例分析[M].北京：北京航空航天大学出版社，2012.

[2]郑纯丹.基于稀疏分解的雷达一维距离像目标识别[D].成都:电子科技大学，2013.

[3]王哲.基于稀疏重构的SAR成像技术研究 [D].西安:西安电子科技大学，2014.

[4]侯坤.基于压缩感知的重构算法研究[D].重庆:重庆大学，2013.

[5]段沛沛，李辉.压缩感知稀疏表示在雷达目标识别中的应用[J].电讯技术，2016，56（1）:20-25．

[6]吴怡之，刘文轩.基于GA的心电信号稀疏分解MP算法改进[J].计算机工程，2013，9（9）：250-253.

[7]肖正安.语音信号稀疏分解的FOA实现 [J].计算机工程与设计，2013（10）:232-234.

[8]高瑞，徐华楠，胡钢.基于GA和过完备原子库划分的MP信号稀疏分解算法 [J].科学技术与工程，2008（4）：914-916.

[9]王丽，冯燕.基于粒子群优化的图像稀疏分解算法研究[J].计算机仿真，2015（11）：363-367.

[10]李佳琪.动压滑动轴承性能数据库和优化设计技术的研究[D].合肥：合肥工业大学，2013.

[11]王永贵，林琳，刘宪国.基于改进粒子群优化的文本聚类算法研究 [J].计算机工程，2014（11）：172-177.

[12]Danieleb，Markdp．Learning dictionaries for sparse approximation using iterative projections and rotations[J]．IEEE Transactions on Signal Processing，2013，61（8）:2055－2065．

[13]王彩云，孔一荟．基于稀疏表示字典优化的雷达高分辨距离像目标识别[J]．南京航空航天大学报.2013，45（6）:837-842.

[14]Gao Q，Duan C D，Fang X B，et al．A study on matching pursuit based on genetic algorithms[C]//Proceedings of 2011 IEEE Third International Conference on Measuring Technology and Mechatronics Automation．New York:IEEE，2011:283－286．

[15]Mashud H，Kaushik M．An improved smoothed l0 approximation algorithm for sparse representation[J]．IEEE Transactions on Signal Processing，2010，58（4）:2194－2205．

[16]宫华，张彪，许可，等.基于粒子群算法的带有运输衔接的应急物资运输路径优化问题[J].重庆师范大学学报：自然科学版，2015（3）：23-29.

[17]张宇航，唐超，姚李孝.基于改进粒子群算法的梯级水电站长期优化调度研究[J].陕西电力，2016（6）：59-63.

Application of sparse decomposition based on particle swarm optimization in radar target recognition

ZHAO Dong-bo1，LI Hui2
（1.School of Electronic Information，Xi'an Aeronautical University，Xi'an 710077，China；2.School of Electronic Information，Northwestern Polytechnical University，Xi'an 710129，China）

The radar high resolution range profile （HRRP） is projected on a super complete Gabor dictionary by Sparse Representation （SR），and recognition of HRRP by extracting the characteristic parameters of dictionary atoms from the signal.The OMP algorithm based on particle swarm optimization（PSO） is improved to reduce large amount of calculation of matching pursuit by using the Strong search ability and the fast convergence rate.Through recognition experiments of the radar high resolution distance profile （HRRP） show that classification effect is better using feature parameters extraction of Gabor atoms，and the OMP algorithm based on particle swarm optimization （PSO） greatly reduced the computation of parameter optimization.

High Resolution Range Profile （HRRP）； Matching Pursuit （MP）； gabor atom； Particle Swarm Optimization （PSO）； feature extraction

TN957.52

：A

：1674－6236（2017）14-0009-05

2016-09-30稿件编号：201609262

国家自然科学基金资助项目（61571364）

赵东波（1979—），男，陕西宝鸡人，博士研究生，讲师。研究方向：雷达目标识别。