基于线性成像系统的光学超分辨显微术回顾∗

胡睿璇 潘冰洋 杨玉龙 张伟华

(南京大学现代工程与应用科学学院,南京大学固体微结构物理国家重点实验室,南京大学人工微结构科学与技术协同创新中心,南京 210093)

基于线性成像系统的光学超分辨显微术回顾∗

胡睿璇 潘冰洋 杨玉龙 张伟华†

(南京大学现代工程与应用科学学院,南京大学固体微结构物理国家重点实验室,南京大学人工微结构科学与技术协同创新中心,南京 210093)

(2017年3月29日收到;2017年6月21日收到修改稿)

随着纳米科学技术的发展,如何打破光学衍射极限,将光学显微术的分辨本领推进到纳米尺度,已经成为光学领域的一个核心议题.在此背景下,过去的三十年间,发展了多种超分辨光学显微技术,并在生物、材料、化学领域取得了一系列令人瞩目的应用.本文以衍射理论为线索,回顾各类基于线性成像系统的超分辨光学显微技术;对以固浸物镜、结构光照明、扫描近场光学显微术、完美透镜以及超振荡透镜为代表的超分辨光学显微技术进行综述,讨论各种技术的原理,对其特点、应用与局限加以总结,并对该领域的未来发展予以展望.

衍射极限,空间频率,超分辨

1 引 言

光学显微术是人类科技史上最重要的发明之一,它将人类视觉的分辨本领从亚毫米,提高到亚微米,极大地拓展了人类在微米尺度上的认知,直接引发了生命科学的革命.虽然早在十七世纪, Leeuwenheok显微镜的分辨率已经达到了微米尺度[1],但直到1873年德国物理学家Abbe提出光学衍射极限,人类才真正从理论上认识光学显微镜的分辨能力并摆脱经验性的镜片制备[2].而今天,随着科技的发展,光学显微镜已不仅在于简单的“看到”,而发展为一门集分辨能力、微区物理与化学分析能力以及超灵敏(甚至单分子)检测灵敏度的平台.而光学显微术也因此成为一门涵盖多个领域的综合性学科,涉及到光的衍射理论[3]、光-物质相互作用理论[4,5]以及微信号探测技术等重要方向[6,7].特别是光-物质相互作用,以及单分子探测在过去的二十年内已经逐渐成长为两个独立的学科,亦有大量的文献综述,故此本文将讨论的范围限制在光学显微术空间分辨能力这一光学显微术的核心议题.

光学显微镜的分辨极限是Abbe所建立的光衍射理论的直接推论,它指出由于光的波动性,光学显微镜的分辨率不可以好于λ/2.后由Rayleigh给出理想点光源像的半高宽,即我们今日天所熟知的瑞利判据[3].为绕过这一物理极限,在过去的一个多世纪中提出了多种超分辨显微术.其中近场光学显微术是最早提出的技术,1928年,Synge[4]提出可以利用亚波长探测器在样品的近场区域采集光信号并逐点扫描成像的方式实现超分辨成像,其中核心的思想是将含有样品细节信息的非辐射成分,即隐失场的信息提取出来.由于实验上的困难,近场扫描成像的想法直到20世纪70年代由Ash和Nicholls[8]在微波波段首次实现,而光学频段上的实现则一直等到20世纪80年代扫描隧道显微技术被发明之后[9-11].今天扫描近场光学显微镜(scanning near- field optical microscope,SNOM)已经发展成为一个庞大的家族,被应用在生物、表面化学、材料分子、纳米器件分析等重要领域[12,13].

随着纳米技术的发展,特别是等离激元光子学与超材料领域的兴起,出现了一类新型的无需扫描的宽场型近场显微技术.其中最具代表性的是超透镜与等离激元显微镜[14-16].这些技术不再需要扫描,只需将超分辨介质、负折射率材料或金属膜放置于样品的近场区域,即可达到超分辨成像的目的.

与近场成像手段相呼应的是基于远场技术的超分辨光学显微术,尤其是基于荧光技术的超分辨光学显微术.特别是近十年间,基于荧光的超分辨显微术已经成为生物成像领域中的重要分支,为了解亚细胞层次的生理过程提供了一种原位、实时、高精度的研究手段.具体而言,基于荧光样品的超分辨显微术可分为两类,即结构光照明荧光显微镜和基于荧光物质的非线性响应的超分辨显微术.前者将照明光的空间频率与样品的空间频率进行混频[17],可将分辨能力提高一倍;后者是以STED(stimulated emission depletion microscopy)、PALM(photo-active localization microscopy)/STORM(stochastic optical reconstruction microscopy)为代表的一类成像方法[12,13,18,19],此类基于荧光的开关特性,通过确定荧光分子的高精度定位而获得超高空间分辨能力.由于在生命科学领域的重要影响,S.W.Hell和E.Betzig因发明STED和PALM技术而于2014年被授予诺贝尔化学奖.

除去以上方法之外,研究者对其他新型远场超分辨手段也进行了不断的探索,其中最有影响力的是超振荡技术(super oscillatory lens)[20].其在物理原理上利用光场在局域的快速振荡来绕过衍射极限,从而实现远场超分辨的目的.使用该技术,研究者已经在光学频段成功演示了光在远场区域的亚波长聚焦与成像.

从上述讨论中可以看出,超分辨技术根据实现的方法大概可以分为两类：仪器层面的超分辨和后处理超分辨.仪器超分辨如近场光学显微镜,将含有超分辨信息的近场细节通过散射引入到远场达到打破衍射极限的目标.而基于后处理的超分辨技术则常基于光和样品的非线性作用,如PALM/STORM.这一方法依赖于样品的一些预知信息,即样品由稀疏的发光点组成,通过计算得到被成像系统丢失掉的信息.事实上,依赖于样品预知信息的光学显微术已经成为一门独立的学科,并有很多综述对此进行了充分的论述[21,22].为了本文理论框架的完整性,我们的讨论限制在第一类仪器层面的超分辨技术.

本文具体组织如下：首先给出线性光学成像系统的理论框架、光衍射极限的物理本源、并讨论打破衍射极限的途径;接下来将按照不同原理对线性超分辨光学显微镜的原理与应用分别进行论述;最后总结并展望光学超分辨领域的发展.

2 线性光学成像系统

迄今我们所看到的绝大多数成像系统都可以看作一个线性的系统,如图1(a)所示,光从样品到像面的过程在数学上可以用扰动与响应来描述：

这里f(r)是携带样品光学信息的光场,g(r)是像, h是光学系统的点扩散函数.这一描述同时适用于相干与非相干系统.对于相干系统,系统对于复振幅为线性,而对于非相干系统,系统对于强度为线性.

数学上为方便讨论,需要把(1)式,映射到动量空间.利用卷积定理,(1)式可写成

是h(r)的傅里叶变换,也叫做传递函数.(2)式从物理上来讲,像是由物通过一个由光学系统定义的、在空间频率上的滤波器的结果.

在自由空间中,只有当k＜2π/λ的信息才能够传播到处于像面的远场,而空间频率大于2π/λ的信息将被束缚在样品表面.为此将H(k)可以看作一个低通滤波器,对应高空间频率信息(k＞2π/λ)将形成隐失波不能传播到像面,从而导致信息丢失.这就造成了所谓的Abbe衍射极限.

上面的数学可以在倒空间(k空间)中用图像描述(图1(b)).类似晶体衍射,成像的过程可以反映在Ewald球与各类型衍射的关系上.其中Ewald球面规定传播系统的带宽,只有球面内的光可以传播.对于薄样品,样品与光的相互作用满足Raman-Nath衍射条件,如图1(b)[23];而样品中的高频信息和光作用后将超出Ewald球,不能传播到远场,如图1(c)所示.

从图1(b)和图1(c)可直观看出要获得超分辨有如下几个途径：1)利用增大环境折射率的办法提高带宽(即,扩大Ewald球),固浸物镜技术(solid immersion lens,SIL)是此类方案的代表;2)结构光照明显微镜(structured illumination microscopy, SIM),利用结构光照明改变F(k),通过和样品光响应(透射、反射、散射等)分布的混频将一部分不能传播的光变为可传播的光场(图1(d));3)近场光学技术(near- field optics,NFO)利用纳米探针局域的提取携带高空间分辨能力的近场光学信息.上述三种方法是在傅里叶变换理论的框架内,而最近人们从衍射理论的适用范围出发提出了基于超振荡效应(super oscillation)的超分辨成像方案,指出H(k)是一个描述全局的函数,对于局域的场变化速度可以大于系统的带宽(即所谓的超振荡效应),从而有可能打破衍射极限.

下面将按照上述顺序,对基于SIL,SIM,NFO和超振荡成像技术进行分别论述.

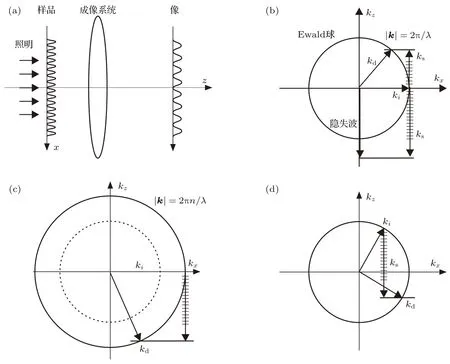
图1 光学显微成像原理的Ewald球表示 (a)线性光学成像系统示意图;(b)传统成像系统;(c)高折射率对分辨本领的提高作用;(d)照明和样品的空间频率的混频效应Fig.1.Ewald sphere and di ff raction conditions for di ff erent optical microscopy techniques：(a)Schematic drawing of an optical imaging system;(b)Raman-Nath di ff raction for conventional optical microscope; (c)high refractive index supports high spatial frequency propagating waves;(d)spatial frequency mixing between the sample and illumination.

3 固浸物镜

从瑞利极限公式可知,波长不变提高空间分辨力最直接的办法是提高物镜端的折射率.今天,此方法已经大量应用于商用显微物镜中,利用浸油的方式,当前物镜的数值孔径可达到1.5左右.而SIL是在油镜的基础上发展而来,其用折射率更大的固体介质来代替油,在固体中光波长变短,波矢变大,从而能够携带更高的空间频率.

固浸物镜的概念来自Born和Wolf的理论[3].这条理论指出了高折射率小球中的两个“等光程点”可以将光线聚焦而不产生球差.基于这两个点相应也产生了两种SIL,即hemispherical SIL(h-SIL)和super SIL(s-SIL).h-SIL利用了第一个“等光程点”——球心(图2(a)).各路光线垂直入射到半球中,不产生球差.同时由于聚焦距离与折射率n无关,也不会产生色差.h-SIL在带来n倍折射率的提升的同时,还带来了n倍的放大倍率.s-SIL则利用了第二个“等光程点”——球心旁R处,不产生球差(n0为小球折射率,n1为周围空气折射率, R为小球半径).s-SIL提供了n2的分辨率提升(受整个系统限制,提升最大为n),以及n2倍的放大倍率,如图2(b)所示[24].

图2 固浸物镜的两种形式 (a)半球形SIL;(b)超级SILFig.2.The two cases of solid immersion lens：(a)Hemispherical SIL;(b)super SIL.

两种SIL都能实现高分辨的表面成像和亚表面成像,但在与样品的接触面要实现折射率匹配(添加折射率匹配油或者压紧).在亚表面成像中,一般的显微镜都要受到样品折射率的影响,整个显微系统分辨率下降为1/n,而s-SIL整个显微系统的分辨率则不会受到影响.其工作距离遵循公式H=R(1+1/n)-D,D为样品内待观测的面位于样品表面之下的距离[24],H为h-SIL的高度.但由于s-SIL的焦距与n有关,使用s-SIL时会产生色差.

h-SIL首先由Mans field和Kino[25]在1990年实现,他们用一块折射率为2的固浸物镜在436 nm的光照明下实现了100 nm的分辨率.随后,s-SIL也被Kino等[26]在1994年实现,他们将780 nm的照明光汇聚成了一个317 nm的光斑,并分辨了500 nm周期的光栅.在这之后,固浸物镜显微术不断发展,很多工作都取得了2—3倍的分辨率提升[27-30],如图3(a)所示.由于其非破坏性的亚表面成像特性,最终在半导体芯片领域形成产业. Serrels等[24]利用s-SIL结合非线性成像技术的增强因子),成功用自由空间1530 nm的波长,获得了约100 nm的分辨率.

近年来,不少学者将固浸物镜缩小到波长尺度,进一步获得了分辨率的突破[31-34].Lee等[32]在2009年制成nanoscale lenses of calix hydroquinone(CHQ),成功地用663 nm的光分辨了250/220 nm的条纹图案(图3(b)).随后Mason等[33]指出,纳米尺度SIL(n-SIL)相对于传统SIL在分辨率上将会有25%的提升.

2011年,Wang等[34]利用直径几微米的SiO2小球,实现了50 nm(λ/8—λ/14)的分辨率(图3(c)),引起了众多关注.值得注意的是此类基于微球成像的工作中,分辨率采用的是最小可分辨的物体边缘间的距离,而不是传统成像理论中物体中心点之间的距离,这在具体参数比较中需要明确.另外,至今该类成像系统的点扩散函数仍未见报道,这也给其详细的性能评估带来了困难.

图3 固浸物镜应用 (a)GaP SIL对染料分子球的超分辨成像[28];(b)纳米光栅的微米SIL成像[32];(c)光栅的微球成像[34]Fig.3. Super-resolution imaging by di ff erent SIL：(a)Fluorescence image of dye nanoball by GaP SIL[28];(b)optical image of nanograting via a polymer microlens[32];(c)super-resolution image of nanograting via a microsphere lens[34].

4 结构光照明显微术

结构光显微术即SIM首先在1963年由Lukosz和Marchand[35]提出,在实空间中,摩尔条纹可以用来简略地说明其原理(图4(a))[17].两个精细度超过衍射极限图案,将他们重叠之后,得到一个精细度低于衍射极限的新图案,这个新图案可以很容易地观察到.重要的是,这个新图案是由原先两个精细图案按一定规律矢量线性叠加而来,如果知道其中一个图案,另一个图案也能知晓.在倒空间中,结构光照明显微术可以得到更好的说明(图4(b)—图4(d)).能够传播的光场的波矢形成了一个圆(图4(b)),圆的半径为kcutoff,空间频率低于kcutoff的可以传播,即圆内的各点都是能够传播的.为了传播圆外的具有高频空间信息的点,我们可以将圆外的点“移到”圆内.这个过程通过携带相应空间频率的照明光与样品相互作用实现.例如,对于一个正弦照明光(图4(c)),其携带三种空间频率(0,±killumination).当它与样品(ksample)相互作用时,会产生(ksample,ksample±killumination)的光,只要这三种空间频率的光有一种低于kcutoff,那么ksample所包含的信息就可以被探测到.

实验中,如何分离交叠的(ksample,ksample± killumination)信息是SIM中的关键,为此研究者们发展了诸多不同的方法.最常用的是相移法,通过对照明光killumination进行相移操作并多次曝光,再按照两种光叠加的规律(相位差)反推,就可将ksample分离出来,并最终重现样品图案[17].从结果上来看这种方法相当于将圆心移动到了圆周上再次画圆(图4(d)),最大形成半径为2kcutoff的圆(图4(e)),即最多将分辨率提升两倍.由于利用的是光强信息,SIM的照明从理论上对光的相干性并不要求,但由于非相干光光源强度较弱,实验中多使用激光光源.

横向[17,36-38]和轴向[39]的SIM很快被开发实现,其中Gustafsson等做了重要贡献.2000年,他们用605 nm的照明光,获得了115 nm的分辨率[17].2008年,Gustafsson等[40]又制成了三维的结构光显微镜,在605 nm的照明光波长下,获得了104 nm的横向分辨率和280 nm的轴向分辨率.几乎同时,Schermelleh等[41]也利用三维结构光照明显微技术实现了对核周缘的彩色成像,获得了与之相当的分辨率.

图4 结构光照明显微术[17](a)摩尔条纹;(b)传统显微镜的Ewald球表示;(c),(d)单一与多方向正弦结构光照明;(e), (f)HeLa细胞边缘蛋白骨架在传统显微镜与结构光照明显微镜下的成像Fig.4.Structured illumination microscopy[17]：(a)Moire fringes;(b)Ewald sphere of conventional microscope; (c),(d)Ewald sphere of sinusoidally striped illumination along one direction and multiple directions;(e),(f)optical image of actin cytoskeleton of HeLa cell with conventional and SIM microscope.

近年来,不少学者将SIM与其他高分辨成像技术,尤其是一些非线性成像技术相结合,实现了远低于100 nm的超分辨[41-44].Gustafsson等[42]制成了饱和结构光照明显微镜,将结构照明光所提供的波矢多次叠加(nkillumination)获得了50 nm的分辨率.随后,Gustafsson等[43]又将SIM与TIRF结合,引入空间光调制器,实现了对活细胞的100 nm分辨率每百点11 Hz的动态成像.

今天SIM技术已经非常成熟并商用化,由于其具备实现相对简单、速度快、可三维成像并对样品要求少的优点,已被广泛应用于超高分辨生物成像领域[45].但由于原理的限制,SIM的分辨能力相比传统成像系统最多只能提高一倍.

5 扫描近场光学显微术

与SIL和SIM技术只对传播光场操作不同,扫描近场光学显微术基于对束缚在样品表面含有高空间频率(即样品细节信息)的隐失波的操作,利用纳米尺度探针将样品近场信息转化为可检测远场信号.从某种程度上,近场光学显微术可以看作是纳米光学领域的主要源头之一.今天,经过三十多年的发展,已发明了大量不同种类的SNOM,并广泛地应用于光学、化学、材料和生物等领域中.

在SNOM中,纳米光学探针占据了核心地位;探针-光场,或者探针-样品的光学作用决定了其关键性能参数,包括空间分辨能力、衬度机理、信号强度等.为此,我们可以通过探针的不同将SNOM分为有孔SNOM、无孔SNOM和发光探针SNOM[46],如图5所示.由于篇幅的关系,基于光力,近场热辐射等特殊近场显微技术在这里不再做回顾[47,48].

图5 主要的近场光学显微镜类型[46](a)有孔探针SNOM;(b)散射型SNOM;(c)探针增强型SNOM; (d)纳米发光探针SNOMFig.5.Four major types of SNOMs[46]：(a)Aperture-SNOM;(b)scattering-SNOM;(c)tip-enhanced spectroscopy technique;(d)nano-emitter tip technique.

5.1 有孔探针SNOM

光学频段的有孔探针SNOM最早由Pohl和Lewis[9,10]独立实现.其核心是利用一个纳米尺寸的通光孔来实现光在纳米尺度的局域化和采集,由于光场局域程度由通光孔的尺寸决定,当通光孔小于半波长时,系统的分辨率将优于衍射极限.

同等重要的是,分辨率的提高(特别是样品激发区域的缩小)也伴随着背景杂散光强度下降,这对实现单分子荧光检测至关重要.利用有孔SNOM的这一优势,1993年贝尔实验室的Betzig与Chichester[49]合作获得了diIC12的单分子荧光图像,达到了高于λ/50空间分辨率,事实上也是人类第一次在室温下获得单分子的实空间光学像,为单分子荧光成像以及以后PALM技术的发明打下了基础.之后,其一直致力于近场光学显微镜的研究并不断提高系统工作的稳定性和分辨率[6,7]. 1994年,Betzig团队[50]又利用S-SNOM实现在室温下对PMMA膜上的荧光染料分子diI进行探测,同样达到了分子级别的空间分辨率.在这一过程中,著名华人科学家谢晓亮[51]也在单分子荧光成像领域做出了重要的贡献.在90年代后期,研究者在该领域亦有所突破,特别是2000年之后,文献[52—54]利用微纳加工技术对光纤探针进行了优化,通过控制激发与收集过程中的光偏振,获得了荧光分子与量子点包括偏振、取向等的大量定量信息.

有孔探针另一类重要的应用是对光场分布的成像,特别是微纳光学器件模式分布的超分辨定量表征[55].这类应用中最常用的技术之一当属光子隧道显微镜(PSTM),其利用锥形光纤探针将束缚于波导或共振腔表面的隐失场散射并耦合至远场,从而获得超高空间分辨的光场信号[56].在此基础上,文献[57]将时间分辨的技术与有孔SNOM技术结合起来,成功的观测到飞秒光脉冲沿波导传播的图像.于此同时,利用各类特殊形状探针对电磁场各向异性的散射效应,超分辨的矢量光场成像已经成为可能[58].

由于在荧光成像领域的成就及前景,在20世纪90年代,有孔探针SNOM领域吸引了大量的研究者加入[54,59].但很快在技术层面上,即分辨率和光信号强度这两核心参数的优化上遇到了不可克服的难题[60].研究者尝试了各种探针设计,特别是锥形光纤探针和金字塔形探针,但当孔径小于100 nm时,信号的透过率将急剧下降,到50 nm时只有不到10-5的光强能够透过微孔.从原理上,纳米孔的超低透过率可以从散射的角度解释.根据巴贝涅原理[3],微孔的散射可以看作磁偶极子的辐射问题,其强度正比于(a/λ)4,所以纳米孔尺寸远小于波长时,其透射效率非常的低[5].

5.2 无孔探针SNOM

无孔探针技术始于20世纪90年代[61],稍晚于有孔探针技术.随着人们意识到有孔SNOM的限制,以及以针尖增强拉曼光谱技术和散射型SNOM技术的突破,在2000年后,无孔探针技术开始成为SNOM领域的主要方向.特别是随着纳米天线理论的发展,新型探针设计以及新的光-物质作用机理的大量的应用为该领域在光谱学、分析和成像领域带来了众多的应用.在这一节里,我们将重点回顾无孔探针SNOM的两个重要分支：针尖增强光谱技术和散射型SNOM技术.

针尖增强光谱技术是无孔探针SNOM中的重要一类,20世纪90年代最早被应用于荧光成像. 1999年,Sánchez等[62]利用15 nm直径的金属针尖的强局域场激发分子双光子荧光效应,由于双光子吸收得到了很好的成像衬度,对荧光染料成像达到了20 nm的空间分辨率;2004年,文献[63]利用Au纳米棒作为纳米天线识别出了单个量子点. 2006年,Novotny课题组[64]研究了在Au纳米颗粒的作用下单分子荧光增强的效果,并发现了当纳米颗粒与单分子距离很近时,由于金属材料的吸收,荧光分子会发生猝灭.之后,Novotny课题组及Sandoghdar课题组都利用Au纳米颗粒作为纳米天线,研究了Au纳米颗粒对样品的荧光增强,单分子的荧光增强达到了10—20倍,相应的激发态寿命也缩短了20倍以上,并且得到了10 nm的空间分辨率[65,66].2007年,Tam等[67]在SiO2纳米颗粒表面镀上Au层,将纳米颗粒修饰到针尖上作为纳米天线,将与其邻近的荧光分子信号增强超过了50倍.而2014年,Wientjes等[68]利用Au纳米棒对捕光复合物LHCII激发,得到了大约100倍的荧光增强,使相应的激发态寿命缩短到20 ps.

但真正让针尖增强光谱技术引起广泛关注的是针尖增强拉曼光谱技术(tip-enhanced Raman spectroscopy,TERS),由于拉曼光谱可用于无标记的化学分析,TERS在各类纳米材料的分析中具有广阔的应用前景.但与荧光不同,拉曼散射效应极微弱,其微分界面约为10-31cm2/SR量级,远小于荧光分子的吸收界面10-16cm2[69].正因为如此,虽然人们在20世纪90年代利用有孔针尖做了大量尝试,但没有获得实质性的成果.直到2000年,文献[70—72]分别独立的报道了针尖增强拉曼效应,利用金属纳米探针尖端对光场的近场增强效应,实现了有机分子大于103倍的增强(图6(a)).之后Hartschuh等[73]成功地将该技术应用于纳米碳管的表征,以30 nm的空间分辨本领观测到了碳管的结构变化(图6(b)).但早期TERS只能应用在具有强烈共振拉曼效应的样品,如染料分子和碳管结构,这种情况一直持续到Pettinger课题组[74]和Zenobi课题组[75]对TERS的探针技术进行了系统性优化,发展出狭缝模式的TERS和低折射率探针金属化办法.利用优化后的系统,本文作者及其他课题组在2007年前后最终将TERS的灵敏度推进到单个分子[76-78].在这期间,亦有课题组报道了单分子TERS实验,但其拉曼峰和其样品并不能对应,不能排除来自与样品污染(特别是无定形碳)的可能[79].

图6 针尖增强拉曼技术 (a)最早的针尖增强拉曼光谱实验结果,银探针可将染料分子的拉曼信号增强40000倍[71];(b)单壁纳米碳管的针尖增强拉曼扫描图像,空间分辨本领优于30 nm[73]Fig.6.Tip-enhanced Raman spectroscopy：(a)40000-fold enhancement of the Raman scattering of dye molecules[71];(b)near- field Raman mapping of singlewalled carbon nanotubes[73].

散射SNOM(scattering-SNOM,s-SNOM)是另一类重要的无孔探针SNOM技术,它和TERS构成了今天最重要的两类纳米光谱分析手段.与TERS不同,s-SNOM的成像不依赖针尖的局域增强效应,而是借助于探针-样品高度局域化的近场光学响应[83].该技术早期的基础主要由德国科学家Keilmann奠定,他从20世纪90年代开始年围绕s-SNOM中的近场相互作用信号提取问题做了大量的基础研究与技术创新,发展出了一系列基于信号调制和解调的办法,并通过探针-样品耦合模型成功的解释了散射信号和样品光学常数间的关系,为s-SNOM奠定了核心基础(图7(a))[84].

至今,结合红外傅里叶光谱技术,s-SNOM已经发展为一项成熟的纳米尺度红外光谱分析技术,可以实现对几乎所有材料的超灵敏超高空间的化学分析[85].2012年,Hillenbrand课题组[86]利用中红外波段的入射光源,对PMMA薄膜上的聚二甲基硅氧烷(PDMS)的红外吸收光谱进行探测,达到了20 nm的空间分辨率.随后,他们又对蛋白质结构的傅里叶变换红外光谱的吸收谱进行测量成像,达到25 nm的空间分辨率,识别出了单个蛋白质复合物[87].2013年,他们又将传统的Si探针尖端用金属Au尖锥代替作为纳米天线,研究了针尖增强红外光谱成像,对单个烟草花叶病毒(TMV)进行红外吸收谱的探测和成像[88].纳米傅里叶红外光谱仪可以实现对半导体、生物矿物、蛋白质纳米结构、单个病毒等表面不同组分的结构进行成像[89].

除对有机物的分析外,散射SNOM也被广泛地应用于无机样品中,特别是新型材料的检测中.例如,2012年,Hillenbrand课题组和Keilmann课题组先后利用散射SNOM和红外激发光对锥形石墨烯纳米结构进行研究,将石墨烯纳米结构转化为可调谐振等离子腔(图7(b))[90,91].又如Basov课题组和Taubner课题组都对由不同的二维材料组成的原子级别薄晶层——范德瓦耳斯晶体的代表六角氮化硼(hBN)进行了探测,改变晶体层数,同时检测红外光谱并成像[92,93].同时,值得注意的是,由于涉及到样品的非定域光学性质(如石墨烯等离激元模式的探测),此类研究中传统基于样品定域光学响应的成像机理模型已经不再适用,故需要新的理论模型.

图7 散射型SNOM (a)最早的超分辨散射SNOM的光学成像图[84];(b)利用散射SNOM采集的石墨烯等离激元干涉图样[91]Fig.7.Scattering SNOM：(a)The super-resolution optical image of Au nanostructures by scattering SNOM[84]; (b)the interference pattern of surface plasmons of a graphene nano-ribbon collected by scattering-SNOM[91].

5.3 纳米发光探针SNOM

上述有孔与无孔探针SNOM都属于被动探针SNOM,而纳米发光探针SNOM则是与之对应的主动发光探针技术.该类技术以纳米发光体(如单量子点、单分子、上转换荧光纳米颗粒或色心)为探针,测量探针所在位置局域的物理参数.由于纳米发光体的发光特性可对局域的光、电、热、磁等物理量有响应,理论上该类探针可以实现多物理场测量[94].同时由于纳米发光体的尺寸非常小,量子点一般小于10 nm,而色心的尺度则在1 nm,故该技术的空间分辨率可以达到10 nm以下,甚至1 nm.

利用纳米发光探针,研究者在过去近20年中取得了一系列的突破.最早Sandoghdar课题组[95]利用单分子修饰的探针实现了纳米结构的高分辨成像.之后,Banin课题组[96]将不同的半导体量子点修饰到探针尖端,演示了在扫描过程中探针尖端的半导体量子点和样品上的染料分子之间的FRET过程.Temirov课题组[97]利用半导体量子点修饰的探针,在低温下扫描Ag(111)表面的PTCDA和NTCDA粉末,真正在纳米尺度下实现了对静电势分布的三维成像.

2.1.2 水土流失严重 全县属半干旱黄土高原梁峁沟壑区，地形支离破碎，沟壑密度大，达2.7 km/km2。由于降水相对集中，土壤质地疏松，植被稀少，山地面积大，造成水土流失严重，表土层逐渐减薄，肥力下降，含水量减少，抗旱能力减弱。且因花椒根系分布浅，水土流失不利花椒对肥料的吸收，容易发生旱情。

虽然具有广阔的应用前景,但由于此类探针的制备难度高,且检测技术复杂,尚处于发展阶段.可以预见,随着纳米加工技术的进步与光学检测技术的发展,纳米发光探针SNOM将会取得快速发展.特别是随着基于纳米金刚石氮缺陷色心荧光的量子计量技术的发展[98],该技术将成为一个重要方向.

6 宽场近场成像技术

扫描近场光学显微术依赖于纳米探针将隐失场转化为可传播的信号,为此需要逐点扫描,因而成像速度较慢.随着纳米光学的发展,特别是等离激元光子学和超材料领域的发展,人们意识到,利用负折射率或负介电常数材料制成的平板也可以支持隐失场,并进一步将其转化为传播场,从而发展出了各种基于超材料和表面等离激元的宽场超分辨光学成像技术.

基于负折射率材料的成像最早由Veselago在20世纪60年代提出.2000年,Pendry[99]从理论上重新考察了基于负折射率材料的成像机理,并证明了双负材料能够用来传递包括隐失波在内的所有的空间频率.虽然人们很早地便在微波波段实现了完美透镜,但是由于磁导率的限制,在可见光波段,这一完美透镜一直无法实现.但近场条件下,对于TM波,只要满足负的介电常数即可,无需考虑磁导率.2004年,Luo和Ishihara[100]用表面等离激元光刻技术记录下周期100 nm(λ/4.4)的干涉条纹.此后,在超材料成像领域,伯克利大学张翔团队做出了一系列的杰出贡献.2005年,张翔等用一块银板(35 nm)对表面等离激元(SPP)增强和传递,最终在光刻胶上形成了60 nm(λ/6)分辨率的像(图8(a))[14].值得注意的是,在这个过程中,仅仅是隐失波的振幅发生了改变,空间频率并未发生改变.2007年,利用双曲透镜的概念,进一步发展出了半圆形的可放大超透镜,分辨率为130 nm (λ/3)(图8(b))[101],并进一步将该透镜与光刻系统结合,实现了高速低成本光刻技术[102,103].2015年,Gao等[104]结合Hyperlens和反射银面实现了22 nm(λ/16)分辨率的超分辨近场成像.除了半圆形之外,还有学者用金属线阵列[105-107]以及独特色散关系的材料做双曲透镜[108-111].

除负折射材料外,利用散射或其他方式也可以实现SPP到传播模式的转化,从而实现宽场成像[112-115].2005年,Smolyaninov等[112]将甘油滴在金层之上并制成抛物线形的边界.通过金层下的棱镜激发SPP,制成了一个二维放大镜.他们用502 nm的氩离子激光照射纳米孔洞阵列样品,获得了60 nm(λ/8)的分辨率(图8(c)).由于SPP的波矢很大,或者说液滴的有效折射率很高,液滴边界对于由外向内传播的SPP相当于一个会聚透镜,而对于由内向外传播的SPP而言,则是一个几乎全角度的全内反射镜.液滴内,SPP按照几何光学的规律,形成放大的像,并最终通过散射转变为传播模式,由液滴上方的普通显微镜观察到.

还有不少学者则将等离激元与结构光SIM相结合,发明了等离激元结构照明显微术(PSIM)[114,115].传统的SIM中,结构光的横向空间频率至多与衍射极限所对应的空间频率相当,因而至多获得普通显微镜两倍的横向分辨率.SPP的横向空间频率可以轻易地达到很大,用作结构光,可以获得更高的空间分辨率.Wei和Liu[114]用442 nm的激光激发508 nm的荧光,用0.85数值孔径(NA)的物镜收集,获得了76 nm(4倍于普通荧光显微镜)的空间分辨率.当然,PSIM的横向空间频率不是没有限制的,横向空间频率越大,SPP在垂直方向的衰减就越快,需要选择一个平衡点或设计复杂结构来增强SPP.

SPP代替散射光来进行暗场显微成像也是一个很好的结合[113].受照明系统数值孔径的限制,传统的暗场显微镜无法获得一个较大的NA(物镜的NA要小于照明系统的NA).Liu课题组[113]用等离激元照明系统取代传统照明,使得物镜可以获得较大的NA.由于SPP只被样品结构散射才能转化为传播模式传播出去,那些没有结构的区域, SPP最终会衰减掉,并不会被物镜收集,这样就获得了很高的对比度.

相比于SNOM技术,基于超材料和表面等离激元的宽场超分辨光学成像技术无需扫描以及相应设备,故速度快、成本低,并对特定样品展示出了出色的成像性能.但此类技术需要将样品放置于超材料或等离激元结构的临近区域,使得样品在选择上受到很大限制;同时其只能对样品表面信息成像,这进一步限制了该类技术的应用.

图8 基于超材料和等离激元的宽场近场成像技术 (a)—(c)使用银质超透镜实现的超分辨成像[14];(d)具有放大功能的超透镜[101];(e)等离激元照明超分辨技术[112]Fig.8.Wide- field near- field optical imaging using metamaterials and surface plasmon：(a)–(c)Super-resolution image by Ag superlens[14];(d)magni fi ed super-resolution optical image with hyperlens[101];(e)SPP based superresolution image technique[112].

7 超振荡透镜

上述成像技术都建立于傅里叶分析理论框架内,其假定光场随空间的变化率的上限由成像系统的带宽所决定,不能快于2/λ,故此两个理想的点光源距离小于λ/2时,经过成像系统后将不能被区分.但在雷达天线设计和高能物理领域中人们发现,在系统带宽受限的情况下,场的局域振荡速度仍可以远快于其带宽所允许的速度,这就是所谓的超振荡现象.因此从原理上讲,在特定情况下如果能够让光场的局域变化速率大于2/λ,两个距离小于λ/2的点将可被区分[116,117].

关于超振荡,Berry和Popescu[116]给出了一个简单的数学例子：

一般情况下,如果N是奇数,f(x)以π为周期振荡.但当a=1时,f(x)=exp(iNx),代表一列波向正方向传播.当a＞1时,在x=0附近,

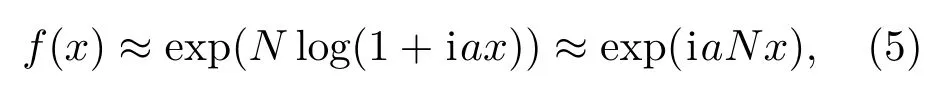
振荡的速率加快了a倍,但从傅里叶展开的角度来讲这是一件有趣的事情.因为

所有的波数都不大于1.也就是说在特定的位置上,函数的变化速率可以高与带宽决定的速度.

利用上述原理,多个课题组做了大量实验和理论工作,通过设计传播函数H(k),实现光在远场范围内的小于衍射极限的聚焦.并且利用该方法对人工纳米结构实现了突破衍射极限的成像,如图9[20,118,119].

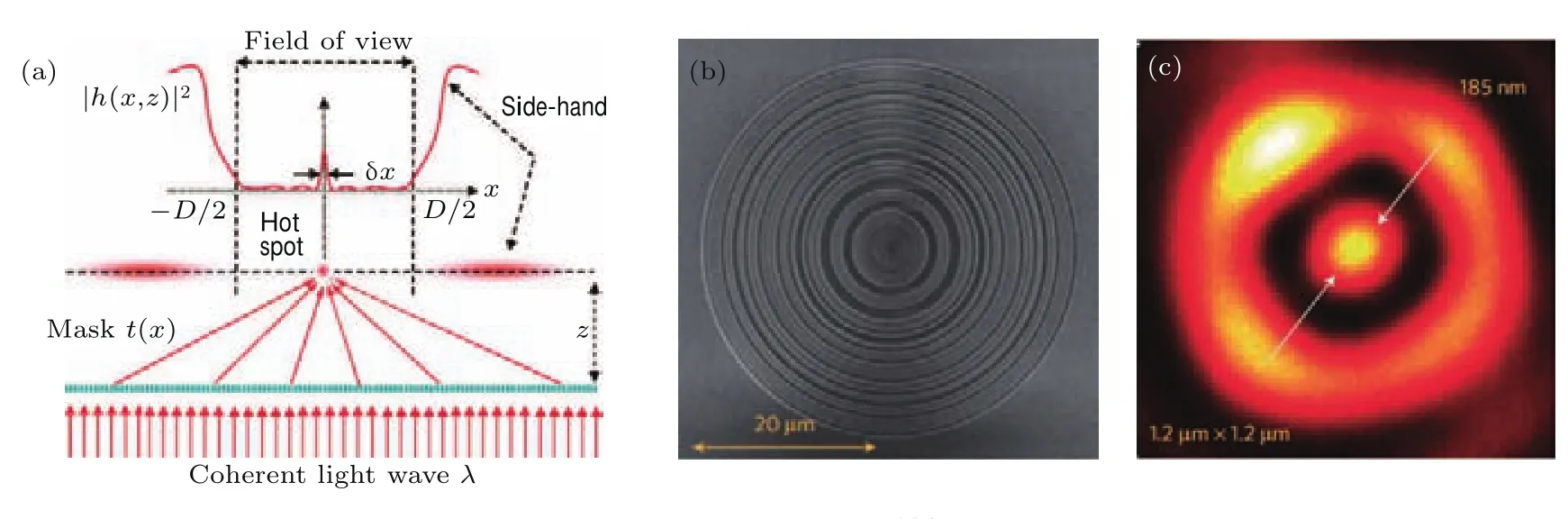
图9 超振荡透镜成像 (a)超振荡透镜纳米聚焦的数值模拟结果图[126];(b)超振荡透镜的电子显微镜图;(c)利用(b)所示超振荡透镜获得的纳米聚焦斑[20]Fig.9.Super-oscillatory lens：(a)Simulated nanofocusing e ff ect by a super-oscillatory lens[126];(b)the SEM image of a fabricated super-oscillatory lens;(c)the measured nanofocus of a super-oscillatory lens[20].

这些工作的核心是超振荡透镜的设计技术.在过去的几年间,为获得最优化的超振荡透镜,人们提出了不同的方法,包括ONSOL[120]、二维环状mask[20]、准晶mask[118]、光学本征模式的mask设计方法[121,122]以及等离激元超表面mask[123].而我国南京大学张勇与肖敏课题组在此领域也做出了独创的贡献,将超振荡的概念与非线性介电超晶格结合在一起,实现非线性的超聚焦[124,125].

需要强调的是超振荡透镜对空间分辨能力的提高是建立在牺牲信号强度和成像范围的基础之上的.在利用超振荡透镜形成打破衍射极限的狭长光锥的同时,必然伴随着强度高数个量级的旁瓣(如图9(a)所示),这给该方法在实际中的应用带来了巨大的困难[119].事实上,也正因为此因素,超振荡现象虽然在传统天线领域已经被发现了近一个世纪,但在实际应用中仍没有得到广泛的应用.同时,通过优化光锥与高强度之间距离往往在波长尺度,这极大地限制了该方法的成像尺寸.

8 总结与展望

超分辨光学显微术在过去三十年间取得了一系列的突破,利用不同的原理,研究者开发了多种基于对成像系统点扩散函数进行修改的硬件超分辨技术.特别是微纳光学以及控制技术的进步,让以扫描近场光学显微镜为代表的近场超分辨技术获得了极大的发展,不仅将光学成像的分辨能力推进到了纳米尺度,同时通过利用局域信号增强、散射、光力等不同探针-样品的耦合作用提供了一系列的探索样品物理化学性质的手段,在材料和表面科学领域获得了众多令人瞩目的结果.同时,以结构光照明技术为代表的远场超分辨光学显微术被提出并已成功的商用化,为生物学的观测提供了一个有效的平台.

而与此同时,在过去十多年中利用光-物质相互作用特性的超分辨光学显微技术亦取得了一系列重大的突破.该类技术的核心机理是通过已知的样品信息,如离散点光源的点扩散函数,恢复被系统过滤的信息,从而打破衍射定律所定的分辨极限.今天,如何将硬件超分辨方法和基于样品预知信息的后处理超分辨方法结合已经成为一个重要的发展方向.特别是如何结合最新关于矢量光学与结构光领域的发展,将光学的偏振与角动量等信息结合成像系统的硬件与图形处理算法,实现高速准确的超分辨显微术将是一个重要的方向[127,128].

另一个值得注意的方向是量子光学领域的发展,在光子数空间上引入了新的维度,这为突破传统基于空间频率空间的衍射极限提供了新的可能性[129].基于这一想法,最近研究者在理论和实验上形成了一系列的突破,成功地演示了两个临近点状热光源的超分辨成像[130].

通过考察超分辨光学显微术在过去三十年间的发展,以及该领域与单分子荧光检测、结构光场、量子计量学等方向的交叉,我们相信如何将硬件对光学传递函数的设计与新兴技术所带来的新的信息有效结合将会在未来为超分辨技术带来巨大发展.这不仅将带来成像领域的突破,同时也将对生命、材料、信息等学科具有巨大的推动作用.

感谢南京大学物理学院祝世宁院士的指导与张利剑教授的讨论.

[1]Bradbury S 1967 The Evolution of the Microscope(London：Pregamon Press Ltd.)

[2]Abbe E 1873 Archiv für Mikroskopische Anatomie 9 413

[3]Borm M,Wolf E 1980 Principle of Optics(New York：Pergamon)

[4]Synge E H 1928 Phil.Mag.6 356

[5]Novotny L,Hecht B 2012 Principles of Nano-Optics (Cambridge：Cambridge University Press)

[6]Betzig E,Trautman J K,Harris T D,et al.1991 Science 251 1468

[7]Betzig E,Trautman J K 1992 Science 257 189

[8]Ash E A,Nicholls G 1972 Nature 237 510

[9]Lewis A,Isaacson M,Harootunian A,Muray A 1984 Ultramicroscopy 13 227

[10]Pohl D W,Denk W,Lanz M 1984 Appl.Phys.Lett.44 651

[11]Binnig G R H 1981 IBM J.Res.Dev.30 355

[12]Thomas A K,Hell S W 1999 Opt.Lett.24 954

[13]Rust M J,Bates M,Zhuang X 2006 Nat.Methods 3 793

[14]Fang N,Lee H,Sun C,Zhang X 2005 Science 308 534

[15]Taubner T,Korobkin D,Urzhumov Y,et al.2006 Science 313 1595

[16]Smolyaninov II,Hung Y J,Davis C C 2007 Science 315 1699

[17]Gustafsson M G L 2000 J.Microsc.198 82

[18]Hell S W,Wichmann J 1994 Opt.Lett.19 780

[19]Betzig E,et al.2006 Science 313 1642

[20]Rogers E T F,et al.2012 Nat.Materials 11 432

[21]Hell S W 2007 Science 316 1153

[22]Jones S A,Shim S H,He J,Zhuang X W 2011 Nat. Methods 8 499

[23]Pohl D W,Kawata S 2001 Near-Field Optics and Surface Plasmon Polaritons(Germany：Springer-Verlag)

[24]Serrels K A,Ramsay E,Dalgarno P A,et al.2008 J. Nanophoton.2 021854

[25]Mans field S M,Kino G S 1990 Appl.Phys.Lett.57 2615

[26]Terris B D,Mamin H J,Rugar D 1994 Appl.Phys.Lett. 65 388

[27]Ghislain L P,Elings V B 1999 Appl.Phys.Lett.74 501

[28]Wu Q,Feke C D,Crober R D 1999 Appl.Phys.Lett.75 4064

[29]Ippolito S B,Goldberg B B,Unlu M S 2001 Appl.Phys. Lett.78 4071

[30]Liu Z H,et al.2005 Appl.Phys.Lett.87 071905

[31]Serrels K A,et al.2008 Nat.Photon.2 311

[32]Lee J Y,et al.2009 Nature 460 498

[33]Mason D R,Jouravlev M V,Kim K S 2010 Opt.Lett. 35 2007

[34]Wang Z,et al.2011 Nat.Commun.2 218

[35]Lukosz W,Marchand M 1963 J.Mod.Opt.10 241

[36]Heintzmann R,Cremer C 1999 Proc.SPIE 3568 185

[37]Frohn J T,Knapp H F,Stemmer A 2000 Proc.Nat. Acad.Sci.USA 97 7232

[38]Gustafsson M G L,Agard D A,Sedat J W 2000 Proc. SPIE 3919 141

[39]Neil M A A,Juskaitis R,Wilson T 1997 Opt.Lett.22 1905

[40]Gustafsson M G L.,et al.2008 Biophys.J.94 4957

[41]Schermelleh L,et al.2008 Science 320 1332

[42]Gustafsson M G L 2005 Proc.Nat.Acad.Sci.USA 102 13081

[43]Kner P,et al.2009 Nat.Methods 6 339

[44]Planchon T A,et al.2011 Nat.Methods 8 417

[45]Demmerle J,et al.2017 Nat.Protoc.12 988

[46]Weisenburger S,Sandoghdar V 2015 Contemp.Phys.56 123

[47]De Wilde Y,et al.2006 Nature 444 740

[48]Betzig E,Finn P,Weiner J 1992 Appl.Phys.Lett.60 2484

[49]Betzig E,Chichester R J 1993 Science 262 1422

[50]Trautman J K,et al.1994 Nature 369 40

[51]Xie X S,Dunn R C 1994 Science 265 361

[52]Matsuda K,et al.2003 Phys.Rev.Lett.91 177401

[53]Moerland R J,van Hulst N F 2005 Opt.Express 13 1604

[54]Taminiau T H,et al.2007 Nano Lett.7 28

[55]Rotenberg N,Kuipers L 2014 Nat.Photon.8 919

[56]Reddick R,Warmack R,Ferrell T 1989 Phys.Rev.B 39 767

[57]Balistreri M,et al.2001 Science 294 1080

[58]Balistreri M,et al.2000 Phys.Rev.Lett.85 294

[59]Veerman J A,et al.1998 Appl.Phys.Lett.72 3115

[60]Dunn R C 1999 Chem.Rev.99 2891

[61]Knoll B,Keilmann F 1999 Nature 399 134

[62]Sánchez E J,Novotny L,Xie X S 1999 Phys.Rev.Lett. 82 4014

[63]Gerton J M,et al.2004 Phys.Rev.Lett.93180801

[64]Anger P,Bharadwaj P,Novotny L 2006 Phys.Rev.Lett. 96 113002

[65]Höppener C,Novotny L 2008 Nano Lett.8 642

[66]Eghlidi H,et al.2009 Nano Lett.9 4007

[67]Tam F,et al.2007 Nano Lett.7 496

[68]Wientjes E,et al.2014 Nat.Commun.5 4236

[69]Kneipp K,et al.2002 J.Phys.14 R597

[70]Anderson M S 2000 Appl.Phys.Lett.76 3130

[71]Hayazawa N,et al.2000 Opt.Commun.183 333

[72]Stöckle R M,et al.2000 Chem.Phys.Lett.318 131

[73]Hartschuh A.,et al.2003 Phys.Rev.Lett.90 095503

[74]Ren B,Picardi G,Pettinger B 2004 Rev.Sci.Instru.75 837

[75]Yeo B S,et al.2007 Anal.Bioanal.Chem.387 2655

[76]Zhang W,et al.2007 J.Phys.Chem.C 111 1733

[77]Ichimura T,et al.2007 J.Phys.Chem.C 111 9460

[78]Domke K F,Zhang D,Pettinger B 2006 J.Am.Chem. Soc.128 147217

[79]Neacsu C C,et al.2006 Phys.Rev.B 73 193406

[80]Pettinger B,et al.2004 Phys.Rev.Lett.92 096101

[81]Steidtner J,Pettinger B 2008 Phys.Rev.Lett.100 236101

[82]Zhang R,et al.2013 Nature 498 82

[83]Knoll B,Keilmann F 2000 Opt.Commun.182 321

[84]Keilmann F,Hillenbrand R 2004 Philos.Trans.A 362 787

[85]Huth F,et al.2011 Nat.Mater.10 352

[86]Huth F,et al.2012 Nano Lett.12 3973

[87]Amenabar I,et al.2013 Nat.Commun.4 2890

[88]Huth F,et al.2013 Nano Lett.13 1065

[89]Hermann P,et al.2014 Opt.Express 22 17948

[90]Chen J,et al.2012 Nature 487 77

[91]Fei Z,et al.2012 Nature 487 82

[92]Dai S,et al.2014 Science 343 1125

[93]Li P,et al.2015 Nat.Commun.6 7507

[94]Jaque D,Vetrone F 2012 Nanoscale 4 430

[95]Michaelis J,et al.2000 Nature 405 325

[96]Ebenstein Y,Mokari T,Banin U 2004 J.Phys.Chem. B 108 93

[97]Wagner C,et al.2015 Phys.Rev.Lett.115 026101

[98]Kühn S,et al.2001 J.Microsc.202 2

[99]Pendry J B 2000 Phys.Rev.Lett.85 3966

[100]Luo X G,Ishihara T 2004 Appl.Phys.Lett.84 4780

[101]Liu Z W,et al.2007 Science 315 1686

[102]Xiong Y,Liu Z,Zhang X 2009 Appl.Phys.Lett.94 203108

[103]Ren G,et al.2013 Plasmonics 8 1065

[104]Gao P,et al.2015 Appl.Phys.Lett.106 093110

[105]Ono A,Kato J,Kawata S 2005 Phys.Rev.Lett.95 267407

[106]Ikonen P,et al.2007 Appl.Phys.Lett.91 104102

[107]Shvets G,et al.2007 Phys.Rev.Lett.99 053903

[108]Han S,et al.2008 Nano Lett.8 4243

[109]Kildishev A V,Shalaev V M 2008 Opt.Lett.33 43

[110]Tsang M,Psaltis D 2008 Phys.Rev.B 77 035122

[111]Li J,et al.2009 Opt.Lett.34 3128

[112]Smolyaninov II,et al.2005 Phys.Rev.Lett.94 057401

[113]Hu H,Ma C,Liu Z 2010 Appl.Phys.Lett.96 113107

[114]Wei F F,Liu Z W 2010 Nano Lett.10 2531

[115]Yuan G,Wang Q,Yuan X 2012 Opt.Lett.37 2715

[116]Berry M V,Popescu S 2006 J.Phys.A 39 6965

[117]Ferreira P J S G,Kempf A 2006 IEEE Trans.Sig.Proc. 54 3732

[118]Huang F M,et al.2007 Appl.Phys.Lett.90 091119

[119]Huang F M,Zheludev N I 2009 Nano Lett.9 1249

[120]Rogers E T F,et al.2013 Appl.Phys.Lett.102 031108

[121]Baumgartl J,et al.2011 Appl.Phys.Lett.98 181109

[122]Kosmeier S,et al.2011 J.Opt.13 105707

[123]Tang D L,et al.2015 Laser Photon.Rev.9 713

[124]Zhang Y,et al.2010 Phys.Rev.Lett.104 183901

[125]Liu D,Zhang Y,Wen J,et al.2014 Sci.Rep.4 6134

[126]Huang B,Bates M,Zhuang X W 2009 Annu.Rev. Biochem.78 993

[127]Chen B C,et al.2014 Science 346 439

[128]Legant W R,et al.2016 Nat.Methods 13 359

[129]Wang H,Han S,Kolobov M I 2012 Opt.Express 20 23235

[130]Nair R,Tsang M 2016 Phys.Rev.Lett.117 190801

PACS:42.25.Fx,07.60.Pb,07.79.Fc DOI:10.7498/aps.66.144209

Brief retrospect of super-resolution optical microscopy techniques∗

Hu Rui-Xuan Pan Bing-Yang Yang Yu-Long Zhang Wei-Hua†
(Collaborative Innovation Center of Advanced Microstructures,National Laboratory of Solid State Microstructures,College of Engineering and Applied Sciences,Nanjing University,Nanjing 210093,China)

29 March 2017;revised manuscript

21 June 2017)

In the last few decades,nanoscience and nanotechnology have been growing with breath taking speed,and how to break through the di ff raction limit and tame the light on a nanoscale have become the major challenges in optics.In this field,several super-resolution optical nanoscopy techniques have been developed,leading to a series of breakthroughs in physics,chemistry,and life sciences.In the work,we give a retrospect of the newly developed techniques in di ff raction theory of linear optical systems,including the solid immersion lens,structured light illumination microscopy,scanning near- field optical microscopy,metamaterial-based wide field near- field imaging technique and super-oscillatory lens.Brief discussion on their principles,advantages and applications is also provided.

di ff raction limit,spatial frequency,super-resolution

:42.25.Fx,07.60.Pb,07.79.Fc

10.7498/aps.66.144209

∗国家重点研发计划(批准号：2016YFA0201104)、国家重点基础研究发展计划(批准号：2015CB659400)和国家自然科学基金(批准号：11374152,11574142,11621091)资助的课题.

†通信作者.E-mail：zwh@nju.edu.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn

*Project supported by the National Key Technologies R&D Program of China(Grant No.2016YFA0201104),the National Basic Research Program of China(Grant No.2015CB659400),and the National Natural Science Foundation of China (Grant Nos.11374152,11574142,11621091).

†Corresponding author.E-mail：zwh@nju.edu.cn