衍射极限尺度下的亚波长电磁学∗
2017-08-08蒲明博王长涛王彦钦罗先刚
蒲明博 王长涛 王彦钦 罗先刚
(中国科学院光电技术研究所,微细加工光学技术国家重点实验室,成都 610209)
衍射极限尺度下的亚波长电磁学∗
蒲明博 王长涛 王彦钦 罗先刚†
(中国科学院光电技术研究所,微细加工光学技术国家重点实验室,成都 610209)
(2017年4月21日收到;2017年5月19日收到修改稿)
作为波的本性之一,衍射是现代物理学的重要研究内容.衍射导致自由空间中波的能量不能被无限小地聚集,从而为成像、光刻、光存储、光波导等技术设定了一个原理性的障碍——衍射极限.对于电磁波和光波而言,尽管通过提高介质的折射率可以压缩衍射效应,但由于自然界中材料的折射率有限,该方法存在很大限制.近年来,随着表面等离子体光学的兴起,表面等离子体在超越传统衍射极限方面的能力和应用前景受到了学术界的关注.本文从亚波长电磁学的角度出发,介绍衍射极限研究的历史,综述了突破衍射极限的理论方法.首先,利用金属介质表面等离子体激元的短波长特性,可将等效波长压缩一个数量级以上,在纳米尺度实现光波的聚焦或定向传输;更进一步,通过人为设计超构材料和超构表面,利用结构化金属和介质中的局域谐振、耦合等特殊电磁响应,可实现亚波长局域相位调制、超宽带色散调控、近完美吸收、光子自旋轨道耦合等,从而突破传统理论的诸多局限,为下一代电磁学和光学功能器件奠定重要基础.
衍射极限,表面等离子体,超构材料,超构表面
1 引 言
波是扰动等物理信息在空间中传播的一种现象,常见的波包括声波、光波、电磁波等.在经典声学、光学、电磁学和量子力学中,处理问题的范围一般在波长量级以上,其根源在于自由空间中波的能量(或概率)不能局域到远小于波长的尺度中.这一现象在量子力学中被称为“不确定性原理”(1928年由Heisenberg提出),对应于光学系统中的“衍射极限”[1].1873年,阿贝指出光学显微镜的成像分辨率存在衍射极限,随后由瑞利通过波动理论进行解释,并指出望远镜和显微镜具有类似的限制[2].一百多年来,衍射极限限制了光学成像技术的发展,导致成像、光刻等光学系统的分辨力难以小于半波长.此外,传统理论一般认为在远小于波长的尺度上(即“长波极限”),波动性逐渐变弱甚至消失.以电磁波为例,在长波极限条件下,电磁场可近似为静电场和静磁场,此时电场和磁场之间的耦合可忽略[3].另外,由不同介质交替排布构成的周期结构在这种条件下具有简单的等效介电常数表达式[4],其电磁特性与结构的微观形式无关,因而无需考虑衍射极限下的具体电磁行为[5].
随着微纳加工和表征技术的进步,许多研究发现当物质的性质在波长尺度范围内发生剧烈变化时,波动方程将变得十分复杂,在特定条件下将出现新的解并导致许多与常识迥异的物理现象[6,7].仍以电磁波为例,当麦克斯韦方程组中介质的介电常数和磁导率随空间迅速变化,传统求解方程组的方法难以应用,必需采用时域有限差分、有限元等数值方法.得益于电子计算机及数值计算能力的提升,近年来亚波长尺度的电磁学取得了快速发展,人们相继实现了负折射率、隐身斗篷、平面透镜、超宽带完美电磁吸收、虚拟赋形等许多传统技术难以甚至无法实现的功能[3,8-13].本文从研究历史、物理现象、机理、材料、器件设计和系统集成等几个方面介绍了亚波长科学技术与传统电磁学和光学的区别,重点针对亚波长结构在超衍射光学、局域相位和偏振调控、宽带电磁吸收和辐射等方面的应用开展讨论.
2 亚波长电磁学的研究范畴
2.1 突破衍射极限
尽管通过电子束、离子束等物理手段或化学合成等方法可以方便地制备出特征尺寸远小于可见光波长的纳米结构,但对纳米结构光学性质的研究直到20世纪末期才出现重要突破.1998年,Ebbesen等[14]发现,金属薄膜上亚波长孔阵列在某些特定波长位置表现出异常透射增强效应(extraordinary optical transmission,EOT):小孔阵列的透射率远大于经典衍射理论的预测结果.该现象引起了学术界的关注[15-17],预示着在亚波长尺度传统光学衍射定律能被打破.Ebbesen等猜测表面等离子体(surface plasmon polariton,SPP)是EOT现象的关键,通过将光子转化为SPP并再次辐射,可极大地增强能量透射率.另外,在金属孔的入射面和出射面四周增加周期性沟槽(图1(a)),可在提高透射率的同时,使出射光定向辐射[18].该定向辐射效应与入射光的波长密切相关,如图1(b)所示,波长580 nm的出射光几乎沿着直线定向传输,发散角仅为±3°;对于波长800 nm的入射光,出射方向将分裂为左右两个级次,其角度可通过SPP的波矢量匹配条件定量计算.基于金属狭缝沟槽结构的定向辐射技术增加了有效口径,突破了传统天线的角分辨率极限,为纳米尺度的光束控制提供了新原理和方法.
除了通过在狭缝外增加沟槽调控电磁辐射外,改变亚波长狭缝的形状也可明显改变电磁波的衍射行为,突破传统基尔霍夫衍射理论的限制.图1(c)为一种悬链线形状的金属纳米孔,具有宽带光子自旋霍尔效应[19]:圆偏振电磁波入射到悬链状狭缝后将改变传播方向,且该方向取决于圆偏振的旋向.图1(d)所示为左旋圆偏振入射时,出射光中右旋分量的电场分布.通过两个悬链线结构的组合(图1(e)),还可产生Bessel光束,在传播过程中消除衍射效应.图1(f)为右旋圆偏振入射时,出射光中左旋分量的电场分布,其中箭头表示左右两部分结构引起的对称性波束偏折效果.显然,在传播过程中交叠部分的光场具有类似Bessel光束的无衍射传输特性.[20].进一步研究表明,通过在二维平面上对悬链线结构进行变形和组合,可实现超宽带的连续型相位调控,构建一系列新型平面光子器件[21-24].
作为一种金属-介质界面上的电子-光子集体振荡,SPP具有短波长特性,其等效波长可达到实际波长的十分之一以下.SPP的传播常数β可写作:
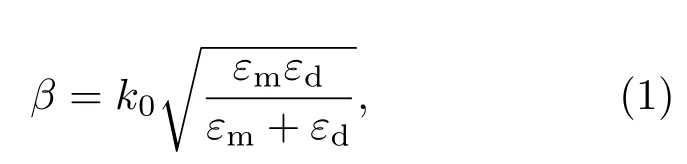
其中εm和εd分别为金属和介质的介电常数, k=ω/c为真空波数(ω为角频率,c为光速).当εm=-εd时,SPP的传播常数取最大值,同时等效波长被急剧压缩.因此,SPP可将光学的研究范畴从远大于波长的“超波长”尺度压缩到远小于波长的“亚波长”尺度.此外,作为一种光子与电子的耦合体,SPP既具有光子的高速度,也具有电子的强局域特性,因而被公认为是一种可以替代电子的通信载体,并以其为基础形成了一门新的学科——表面等离子体光学(plasmonics)[25,26].
SPP的短波长特性可通过其色散曲线分析.如图2(a)和图2(b)所示,金属薄膜的结构对SPP的色散有较大的影响,通过介质-金属-介质或金属-介质-金属结构,并改变薄膜的厚度,能让普通金属-介质界面上的SPP模式互相耦合,从而调节色散曲线.以单层金属薄膜为例(图2(a)),薄膜的厚度越薄,在同一频率处SPP的横向波矢越大,对应的等效波长越短.类似地,在由金属-介质-金属构成的狭缝中,等效波长也与狭缝宽度成正比,对应的等效模式折射率(真空波长与等效波长之比)随着狭缝宽度变小而增大.如图2(c)—图2(e)所示,通过渐变地改变结构的宽度,可以高效地将光波耦合到远小于波长的纳米尺度.
2.2 在衍射极限尺度上操控波
除了“表面等离子体”外,亚波长电磁学的主要研究范畴还包括“光子晶体”和“超构材料”,它们为亚波长尺度上波的调节提供了有效手段.“光子晶体”的概念来源于麦克斯韦方程组与薛定谔方程的类比.众所周知,薛定谔建立量子波动方程的重要一步即是将经典波动方程写作本征值问题,并将德布罗意关系代入.光子晶体的研究采用了与之类似的方法,20世纪末期,Yablonovitch等[30]将麦克斯韦方程组转化为本征值问题,证明了通过人为构造类似于晶体的周期性光学结构,可以得到“光子带隙”材料,使得可以像操控电子一样控制光,将“二极管”,“晶体管”等电子学概念移植到光子学中,使光子计算等研究领域向前迈进了一大步.光子带隙材料可以认为是一种频率选择器件,通过电磁波在不同单元多次反射的相干叠加,实现特定频率的选择性反射或透射.如图3(a)所示,当电子导带的带边位于光子带隙中间,电子自发辐射产生的光子不能传播,从而受到抑制,这种奇特的性质在半导体光电子器件中具有重要应用.近年来,出现了多种基于光子晶体的微纳光子器件,比如光子晶体波导、光子晶体光纤、光子晶体滤波器、光子晶体激光器、非线性光子晶体、可调谐光子晶体等[31-35].同时也产生了很多基于光子晶体结构的新技术,比如纯介质零折射率材料、光子晶体偏振分束器、无源辐射制冷、光子拓扑绝缘体[36-39]等.图3(b)和图3(c)所示为一种基于光子晶体的光学拓扑绝缘体,通过螺旋波导可在本来的带隙中引入手性边缘态,从而让光局域在边缘传播[37].值得注意的是,光子晶体的带隙特征与其晶格常数密切相关,当晶格常数变化,带隙可能消失,从而表现出完全不同的电磁特性[40].

图1 纳米狭缝结构中的异常衍射效应 (a)金属狭缝-沟槽结构的扫描电镜图[18];(b)两个波长的角分辨透射强度曲线,插图为结构及衍射效果示意图[18];(c)单个悬链线结构的电镜图[19];(d)左旋圆偏振入射,右旋圆偏振出射光强分布[19];(e)变形悬链线结构的电镜图[19];(f)变形悬链结构对应的光场分布[19]Fig.1.Extraordinary di ff raction e ff ects in structured nanoslits:(a)Scanning electron microscopy(SEM)of the nanoslit surrounded by periodic grooves[18];(b)angular transmission-intensity distribution at two selected wavelengths,inset is schematic diagram of the structure showing the corresponding dependence of the directionality on wavelength and the beam divergence in the far field[18];(c)SEM image of a single catenary-shaped nanoslit[19];(d)electric field distribution of the cross-polarized component for left-handed circular polarization(LCP)incidence[19];(e)SEM image of a deformed catenary aperture[19];(f)electric field distribution of the cross-polarized component for right-handed circular polarization (RCP)incidence[19].

图2 表面等离子体的短波长效应 (a)金属薄膜上SPP的色散曲线[27];(b)金属狭缝中SPP的等效折射率与狭缝宽度的关系[28];(c),(d)锥形金属狭缝的扫描电镜图和电磁场分布模拟结果[29];(e)由金属薄膜构成的锥形结构电镜图[29]Fig.2.The short wavelength e ff ect of SPP:(a)Dispersion diagram of the SPP on a thin metallic fi lm[27]; (b)the dependence of the e ff ective refractive index on the slit width for the SPP guided by a metal-insulatormetal waveguide[28];(c)a SEM image of a typical V-groove cross-section[29];(d)theoretical modeling of the plasmon coupling,propagation and enhancement in a fabricated tapered groove[29];(e)a tapered section of a gold fi lm on a sapphire substrate[29].
“超构材料”又称超材料,是一种人为构造的新型结构材料,具有超越自然材料的奇异物理(电磁、声学等)特性.超材料的基本思想是通过在亚波长尺度调控结构单元(称为“超级原子”或“超级分子”),实现对材料等效参数的控制.由于超材料介电常数和磁导率的各个分量可在[-∞,∞]范围内任意调节,表现出负折射率、零折射率、高折射率、各向异性、手性等多种特征,材料中的电磁波具有许多与传统材料迥异的传播行为,如负折射、沿变换光学设计的虚拟空间无衍射传输[41-43]等.2010年《Science》杂志将超材料评为过去十年人类最重大的十大科技突破之一.在《Nature》杂志社2010年评选的23个光子学里程碑工作中(其中近30年有6个),光子晶体、表面等离子体和超构材料占据了其中3项[7].
随着理论和实验研究的快速发展,近年来“表面等离子体光学”,“光子晶体”和“超构材料”之间产生了深度交叉融合.特别地,表面等离子体光学和超构材料的融合催生了一个新的研究方向——“超构表面”[44,45].结合表面等离子体的“表面”特性和超构材料中的“亚波长结构”,超构表面可在二维平面或曲面上实现对电磁波的任意调控.根据惠更斯原理,超表面不仅保留了传统超材料的独特电磁特性,更具有超薄、易加工、易共形等优势,被视为超材料实用化的最有效途径[44].如图4(a)所示,基于超构材料的电磁隐身斗篷可使其中的电磁波按照设计要求弯曲,从而绕过被隐形物体[8].基于超构表面的电磁调控材料如图4(b)所示,通过调节表面上的相位分布,可任意控制电磁波的反射方向,从而改变该表面的电磁外形,实现电磁外形和几何外形的解耦[13].外形解耦还可用于构造共形的多功能光学器件,在任意曲面上实现所需的光学功能[46].
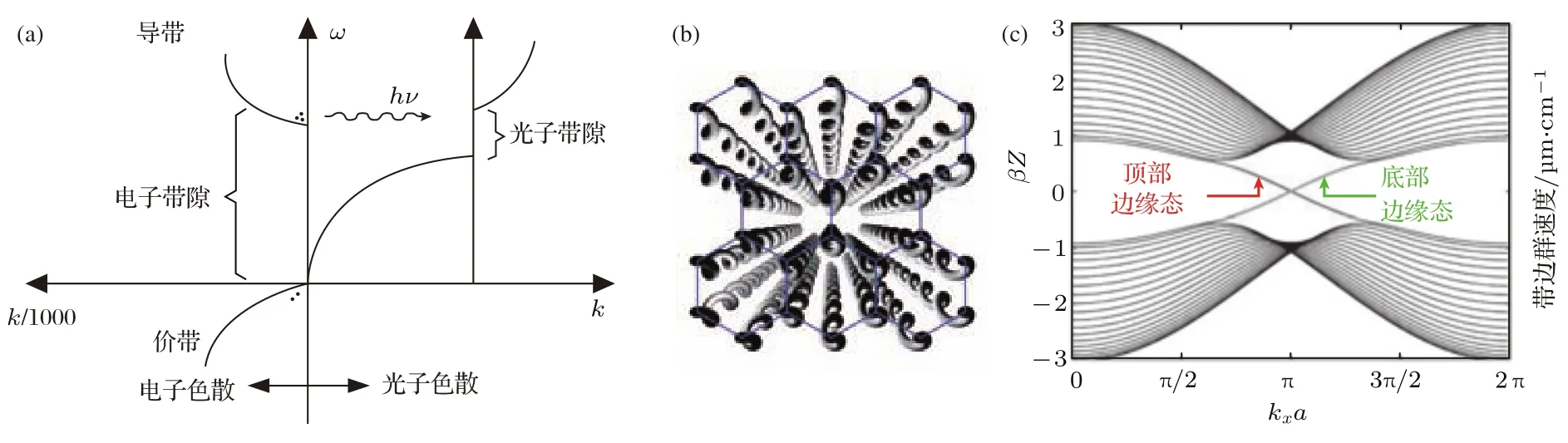
图3 (a)电子晶体与光子晶体的能带图[30],当电子导带的带边位于光子带隙中间,自发辐射产生的光子不能传播,从而抑制自发辐射;(b)基于螺旋光子晶体的拓扑绝缘体;(c)螺旋光子晶体的能带图Fig.3.(a)Energy band diagram of the electron crystal and photonic crystal[30],right-hand side,the electromagnetic dispersion,with a forbidden gap at the wave vector of the periodicity;left-hand side,the typical electron wave dispersion of a direct-gap semiconductor;the dots represent electrons and holes;(b)photonic topological insulator based on helical waveguide;(c)energy band of the helix waveguide.
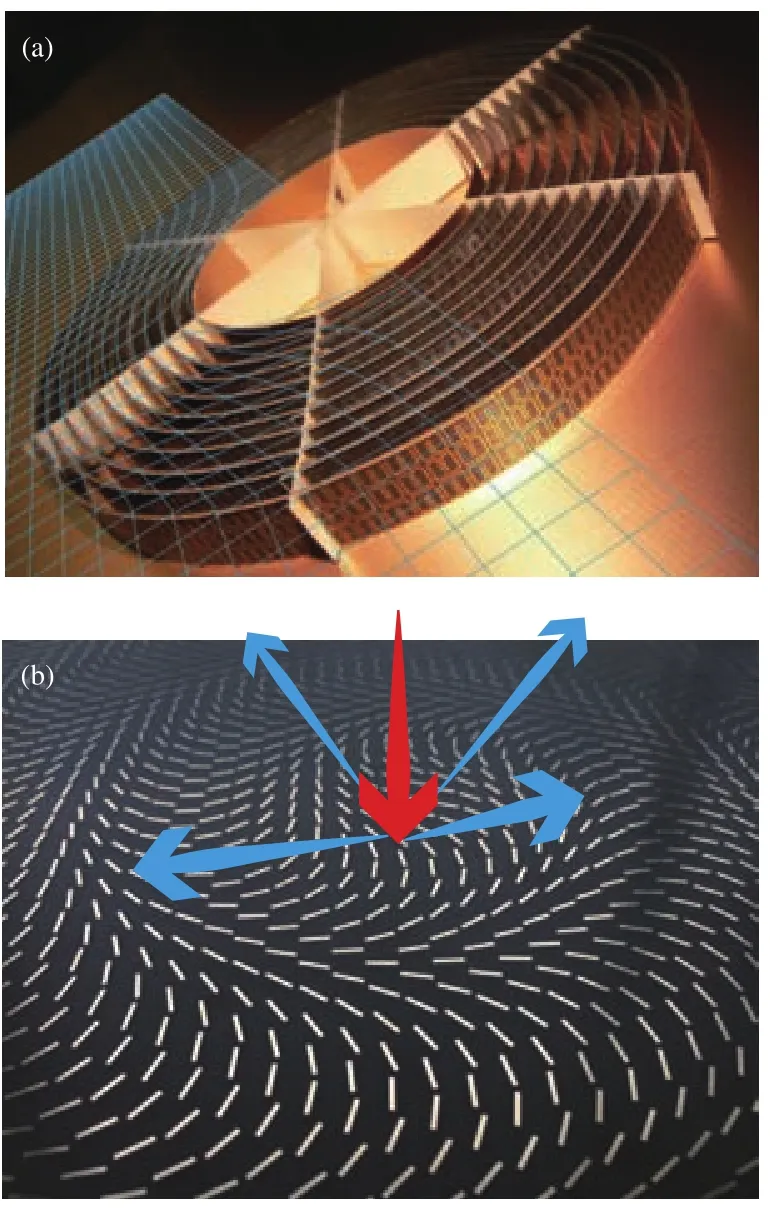
图4 超构材料与超构表面 (a)基于变换光学设计的微波隐身罩[8];(b)基于自旋-轨道相互作用的超构表面[13],红色为入射波,蓝色为反射波Fig.4.Metamaterials and metasurfaces:(a)Microwave invisibility cloak designed by transformation optics[8]; (b)metasurfaces based on spin-orbit interaction[13].
2.3 超构表面上的电磁波及其属性
从麦克斯韦方程组可知,本构参数、初始条件和边界条件是求解电磁问题的数学基础.超材料(三维亚波长结构)的核心思想是利用亚波长结构合成具有等效本构参数的人工复合材料,实现对电磁波的任意调控.对于超构表面结构(以下简称超表面)而言,由于其厚度远小于波长,可将其等效为一种人工设计的边界条件[1,47].根据边界和体的映射关系,边界条件与本构参数对电磁波具有类似的调制效果.
尽管超表面结构在近年来才得到学术界的关注,其研究历史却可追溯到20世纪初.1902年, Wood观测到金属光栅的异常反射光谱[48],后来被证明与SPP的激发有关[49].同年,Levi-Civita给出了超薄金属薄膜的等效边界关系[50],后来被广泛用于电磁界面问题的分析.这两个发现分别促进了SPP和频率选择表面理论的发展.近年来,基于超表面结构的器件被广泛研究,并成功地应用于光谱滤波、表面等离子体光学器件、振幅和相位调制器件、完美吸收材料等[51-55].超构表面的奇特电磁特性可通过表面上的电磁波(简称“超构表面波”)进行阐述,其属性是新型超表面器件的物理基础[1,56],以下予以简单介绍:
2.3.1 短波长属性
如2.1节所示,SPP的等效波长可远小于真空波长,对应的模式折射率(传播常数与真空波数的比值)远大于1.在436 nm波长,SPP的等效波长可达到X射线量级[57].短波长属性是突破衍射极限,实现超分辨成像、存储和光刻的物理基础.对于金属-介质复合膜层,由于不同界面上SPP的耦合,混合SPP色散曲线可以大范围调节,进一步缩短等效波长.以金属-介质-金属或介质-金属-介质结构为例,混合SPP的传播常数可通过以下公式计算[1,27]:
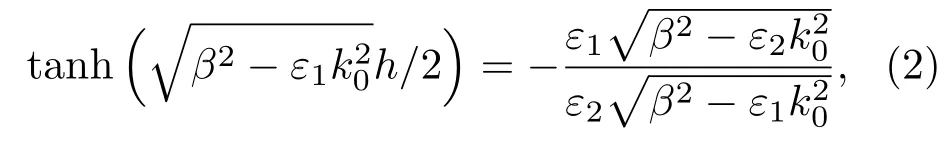
其中ε1和ε2分别为金属或介质的介电常数,h为中间膜层的厚度.计算表明,当h小于20 nm,混合SPP的等效波长可降低到真空波长的1/10以下.
除了SPP外,我们注意到通过超材料也可以构造等效高折射率材料,从而缩短波长[58],但由于其复杂的结构,目前只在微波、太赫兹等低频段验证,尚难以应用于光波段.
2.3.2 相位可调属性
相位调控是光学和微波领域的重要研究内容之一,是波前变换、相控阵雷达、偏振调控等应用的关键.根据折反射定律,传统相位调控元件一般是通过改变不同位置处材料的厚度,利用传播引起的相位延迟调控波前.由于超构表面波可以突破衍射极限,使得相位、振幅等信息得以在亚波长尺度进行任意调控,从而将传统的曲面设计和制备难题转化为平面亚波长结构的设计和制备.根据引入相位的机理进行分类,目前相位调控的方法主要有介质光栅、金属狭缝或孔、金属或介质谐振器、PB(Pancharatnam-Berry)几何相位[11,21,59-63]等.以金属狭缝为例,由(2)式可知,通过梯度式地改变狭缝的宽度,可使入射电磁波偏折到任意指定角度[9,64].同时,通过调节表面阻抗,还可以改变传统Fresnel公式,调控折射和反射的强度[1].从理论层面讲,具有梯度相位分布的超构表面器件可以改变传统折反射行为,形成“广义折反射定律”[10,65].此外,通过两个正交方向的相位延迟调控,还可以实现任意偏振调控,以及基于偏振调控的自旋轨道相互作用[13,66-70].
2.3.3 色散可控属性
频率色散指材料对不同频率的光波有不同的响应.由于电磁波具有极宽的频谱,运用超表面的色散来调制不同频率的波具有重要意义[71].色散特性可广泛应用于以超表面为基础的宽频带器件,如宽带波片、完美电磁吸收器以及宽带相位调控器件[12,72,73]等.依据麦克斯韦方程组及边界条件,容易推导出完美电磁吸收器和宽带波片所需的色散关系[66,74].对这两种应用而言,色散要求十分相似,但由于理想色散曲线违反了Kramers-Kronig (K-K)关系及因果律,因此理想色散关系只能在一定程度上逼近,导致吸收和偏振转换器件存在厚度-带宽极限:一定厚度条件下器件的带宽存在上限[75,76].研究表明,Lorentz模型是实现宽带吸收和偏振转换的有效途径[12,67,73].由于复杂的超表面可通过一系列串联和并联电路描述,其等效色散曲线与Lorentz模型一致,满足因果律和K-K关系.这一色散理论可为宽带器件的设计提供理论指导.譬如,利用色散补偿的宽带波带片可实现宽带自旋-轨道耦合[13],利用软表面的色散可在宽带范围内降低喇叭天线的旁瓣[77].除了普通的Lorentz色散之外,通过引入外加激励构造负阻抗器件可进一步调控色散关系,突破被动材料的厚度-带宽极限[78].
除频率色散之外,在某一频率或波长处电磁波不同方向波矢量之间的关系也被称为色散关系.在非磁性的单轴晶体中,光波的色散方程一般可写作


图5 双曲色散 (a),(b)基于金属介质多层膜构成的双曲色散材料;(c),(d)双曲色散和普通材料中的频率等高线和能流方向Fig.5.Hyperbolic dispersion:(a),(b)Hyperbolic metamaterial based on metal-dielectric multilayers; (c),(d)the equifrequency curves and energy fl ow directions in hyperbolic and normal materials.
其中kx,ky,kz分别为x,y,z方向的波矢量值;ε//和ε⊥为电场平行及垂直于晶体主轴(z轴)时的介电常数.在普通晶体中,ε//和ε⊥均为正值,对应的频率等高线为椭圆.在由如图5(a)和图5(b)所示的金属-介质多层膜构成的等效材料中,由于金属介电常数为负,ε//和ε⊥可具有相反的符号,对应的频率等高线为双曲线.图5(c)和图5(d)为双曲色散和普通色散材料中的频率等高线(蓝色实线)和能流方向(红色箭头,即群速度方向).根据群速度的定义vg(ω)=∇kω(k)可知,对于双曲色散材料,除了临近原点的小部分区域,能流方向基本沿着渐近线的法线方向[79].因此,双曲色散材料可使电磁波在其中定向传输,为突破衍射极限提供了一种新的途径.另外,由于只有横向波矢kx大于一定值的高频分量才能传播,双曲色散材料可作为高频空间滤波器使用[80].
3 亚波长电磁学的典型应用
3.1 基于SPP的超衍射光刻
如前文所述,以SPP为代表的表面波最引人注目之处在于其可以突破传统光学的衍射极限.基于此,SPP在包括显微成像、光学光刻、光波导、光存储等技术中取得了成功的应用[57,81-83].其中,基于SPP的成像光刻技术在近年来发展迅速,已经在365 nm波长实现22 nm特征尺寸的光刻效果[84,85],结合后续工艺可实现8 nm以下特征尺寸图形的制备.
图6(a)为一种实现SPP超分辨光刻的典型器件,通过综合两种典型的超衍射机理(腔共振,通过金属-介质-金属三层膜系实现;Bessel光束,利用环形光栅结合金属-介质多层膜的高阶波矢定向滤波特性实现[79]),该器件可在长工作距模式下实现超分辨聚焦(62 nm线宽,100 nm工作距,365 nm波长)[80],提供了一种突破“近场衍射极限”的“虚拟探针”[86].金属-介质-金属谐振腔可以进一步提高SPP激发效率,抑制腔内电场纵向分量并减少其对成像性能的负面影响,获得更高分辨力和对比度的成像光刻效果.相比于反射共振结构,共振腔透镜结构可将曝光深度拓展约2倍.基于该方法,在实验上获得了深度23 nm光刻胶图形,并得到了约1/17波长线宽光刻分辨力实验结果,如图6(b)所示[84].图6(c)为基于上述原理研制的SP光刻机,目前已具备移动曝光、高精度套刻等功能.

图6 基于SPP的超衍射传输和超分辨光刻技术 (a)通过SPP产生超衍射虚拟探针的结构示意图[80];(b)22 nm线宽图形的电镜图[84];(c)表面等离子体光刻机照片Fig.6.Subdi ff raction propagation and lithography based on SPP:(a)Schematic of the generation of virtual probe using SPP[80];(b)SEM image of the fabricated sample with 22 nm half-pitch[84];(c)image of the lithography system.
基于SPP的光刻技术从光学系统层面上突破分辨力衍射极限,无需引入双光子、受激发射损耗、光吸收调制等特殊非线性光学效应,在材料和工艺上保持了与传统光学光刻技术的兼容性,有望成为一种低成本、大面积、高效的纳米光刻加工技术[25,87].当然,当前SPP光刻技术仍然有一些问题需要进一步深入研究.在原理方法方面,需要研究探索SPP超分辨成像光刻新方法;在技术层面,需要发展配套的SPP光刻控制技术;在工艺和材料方面,需进一步研究光刻分辨力增强技术,提升光刻图形质量,并完善后续图形传递工艺.
3.2 基于广义折反射定律的平面光学器件
在普通折射现象中,两种材料界面上的相位不存在跃变,因此可通过相位匹配条件推导传统折射定律(即Snell定律).通过在材料界面上人为施加随位置变化的梯度相位,可改写传统折射定律,实现任意方向的折射[9,10,47].此外,与各向异性材料界面上的广义折射定律不同[88],引入梯度相位后反射定律也不再适用.由于这种相位梯度可通过超构表面实现,此类广义折反射定律也被称为超构表面辅助的折反射定律(metasurface-assisted law of refraction and re fl ection,MLRR)[1].
在MLRR中,控制折反射方向的关键在于恰当地引入相位梯度.目前主要有三种引入相位梯度的方法:其一是梯度折射率材料,通过在空间上改变介质光栅的占空比,或利用几何尺寸渐变的超构材料都可引入类似的相位梯度[59,60].由于普通介质材料或等效超构材料的折射率有限,为了实现360°的相位变化,材料的厚度需要接近甚至远大于波长,且不同单元存在遮挡、耦合等不利效应.第二种方法利用了金属介质界面上SPP的短波长特性,通过将宽度渐变的纳米狭缝垂直排列,可在不同位置局域地引入任意相位差[9,64,89,90].由于SPP的等效波长极短,对应的模式折射率远大于普通材料,因而可使器件的厚度远小于波长.第三种引入梯度相位的方法利用了超构表面中的几何相位[10,21,62,91].不同于在传播路径上的累积相位,几何相位只取决于平面结构的几何形状和尺寸,与材料的厚度无关.因此,这种器件仅需远小于波长的厚度即可产生任意相位梯度,实现对折射和反射方向的精确调控.
相位梯度超构表面可用于构建平面透镜、轨道角动量(OAM)产生器、高阶Bessel光束产生器等一系列新型光学器件[52,92,93].基于MLRR的平面透镜可以将电磁波聚焦到任意指定距离,在显微、望远等领域具有广泛的应用前景.图7(a)所示为一种基于超构表面的物镜,每个单元由旋转的各向异性纳米介质柱构成,通过光子的自旋-轨道相互作用实现局域相位调控.该物镜的放大倍率最高可达170倍,图7(b)和图7(c)分别为离散物体及其成像效果[62],图7(d)为基于平面纳米结构的望远成像系统,图7(e)和图7(f)分别为红光和白光的成像星点图,其像质已接近衍射极限[65].
MLRR还可推广到更复杂的应用场合中.比如,相位型平面器件可作为波前校正元件,用于传统光学系统中替代折射型透镜,消除各种像差.通过超构表面构建复杂的梯度相位分布,也可将入射光折射到指定的位置,实现分束、三维彩色显示等功能[94-96].此外,通过调控材料表面的反射行为,可使入射能量不返回到原方向,极大地减小目标的光学或雷达散射截面[13,97].

图7 基于超表面的显微物镜和望远镜主镜 (a)超构表面显微物镜的电镜图,标尺300 nm[62];(b)字符“H”的电镜图,标尺10µm[62];(c)成像效果,标尺10µm[62];(d)望远系统照片[1];(e),(f)红光(波长632.8 nm)及白光星点图[1]Fig.7.Microscope and telescope based on metasurface:(a)SEM image of the metasurface objective,scale bar 300 nm[62]; (b)SEM image of the object“H”,scale bar 10µm[62];(c)image of the object,scale bar 10µm[62];(d)photograph of the metasurface-based telescope[1];(e),(f)focal spots for red light(left,λ=632.8 nm)and white(right)light[1].
3.3 从色散工程到超宽带电磁调控
如前所述,电磁模式的色散在几乎所有亚波长结构及器件中均具有重要意义.一方面,我们可从SPP的色散特性直接推导出其短波长属性[27].另一方面,基于这些模式的频率色散,可以构造多波长、超宽带或超窄带的电磁器件[98-100].
在设计宽带电磁器件时,首先通过数理模型推导出完美电磁器件所需的频率色散,然后通过亚波长结构对其进行模拟和逼近.对于超表面吸波材料而言,理想色散曲线可通过传输矩阵推导[12,66].课题组前期已证明通过超构表面模拟理想吸收层的色散特性,可在不增加厚度的条件下极大地提高吸波材料的带宽,在一个倍频程范围内吸收率大于97%,如图8(a)和图8(b)所示[12].理论分析发现,这种带宽拓展现象得益于金属层色散曲线从Drude模型向Lorentz模型的转换.其中Lorentz谐振来自于结构化金属中束缚电子的共振,与金属中电子在红外波段的带间跃迁具有类似之处.值得注意的是,在相干入射条件下,采用Drude模型即可实现频率无关的超宽带吸收,且最小厚度仅需
0.3 nm[101,102].
与传统块体吸波材料不同,在亚波长结构的吸波材料中,自由空间中的入射电磁波会被亚波长结构转化为局域电磁模式,通过临界匹配实现完美吸收[45].这些局域模式对吸波性能的提升有两方面的好处:首先,通过将电磁波由纵向传播转换为沿表面横向传播,可降低对材料厚度的要求,实现超薄电磁吸收体;其次,通过局域模式的谐振和电磁增强,可使电磁波的吸收率大幅增加,并为色散调控提供谐振单元,从而进一步拓展吸收带宽.
与吸收材料设计类似,通过各向异性超表面的色散,可实现宽带偏振转换.在一维色散调控的基础上[66],通过二维方向的色散调控原理上可进一步拓展偏振器件的工作带宽[73].如图8(c)和(d)所示,在开口谐振环的两个正交方向采用Lorentz谐振子的叠加进行宽带色散调控,可在5:1的带宽范围内实现消色差偏振转换.

图8 基于色散调控的宽带亚波长电磁器件 (a)基于十字形单元结构的宽带吸波器[12];(b)超表面吸波器和Salisbury吸波器吸收率的对比[12];(c)基于开口谐振环的宽带偏振反射镜[73];(d)交叉偏振转换率的模拟和测试结果[73]Fig.8.Broadband meta-devices based on dispersion engineering:(a)Schematic of the broadband absorber based on metasurface dispersion engineering[12];(b)absorption at normal incidence as a function of frequency,the Salisbury absorption curve is shown as a reference[12];(c)perspective view of the polarizing metamirror based on split ring resonators[73];(d)simulated polarization conversion ratio(PCR)from LCP to LCP(blue solid line)and measured polarization conversion ratio from x-to y-polarization(red asterisk)[73].
在各种电磁器件的实际应用中,需要针对应用环境对器件的材料和工艺进行优化.特别地,很多情况下(如太阳能热光伏系统、高速飞行器)吸波材料需要在高温环境下工作.针对这种需求,近年来出现了多种基于耐高温材料(如TiN,W,Mo,镍铬合金等)的设计和实验[103,104].以TiN材料为例,由于其熔点高达2930°C,且在可见-近红外波段具有等离子共振特性,被广泛用于红外吸波材料的研究.如图9(a)所示,基于TiN的吸波材料可在400—800 nm波段实现95%以上的吸收率.通过退火和激光加热对该材料的耐高温特性进行研究,发现材料在800°C退火后性能几乎不变.作为对比,基于贵金属的吸波材料在退火后结构发生了严重变形,导致性能丧失,如图9(b)和图9(c)所示.

图9 基于难熔材料的高温吸波器件 (a)TiN吸波器在退火前后的吸收率测试结果[103];(b)TiN吸波器经800°C退火后的表面电镜图[103];(c)Au吸波器经800°C退火后的表面电镜图[103];(d)镍铬合金吸波材料的照片和电镜图[1]; (e)镍铬合金表面加热前和加热后的电镜图[1];(f)不同温度下反射率的实测结果[1]Fig.9.Refractory-material-based absorbers:(a)The measured absorption of the TiN absorber after annealing at 800°C for 8 h,as well as the reference measured absorption of TiN before annealing[103];(b),(c)the SEM images of the TiN and Au absorbers after annealing[103];(d)photography and SEM image of the NiCr absorber[1];(e)SEM image of the NiCr surface before and after heating[1];(f)measured absorbance of the NiCr absorber at various temperatures[1].
图9(d)—图9(f)为本课题组前期在微波段研制的系列耐高温吸波材料.采用镍铬合金和SiC陶瓷,该吸波材料能承受1200°C以上的高温环境[1].另外,采用色散调控原理,该吸波材料的带宽相比于普通材料也提高了约两倍.
4 总结与展望
亚波长电磁学是研究物质与电磁波在亚波长尺度(即小于衍射极限的空间)相互作用的现象、规律、机理及应用的学科,其主要研究内容可根据结构形式和电磁响应特征进行分类,通常包括表面等离子体、超材料、超表面和光子晶体等几个研究领域.当然,当前很多电磁器件和系统中,各种基本概念彼此渗透,相互交叠.例如在基于金属介质多层膜的双曲色散材料中,表面等离子体、超材料、光子晶体理论均可从不同层面对其电磁特性进行分析[80,105].
在亚波长电磁学的各个研究方向中,亚波长结构材料是亚波长科学的物质载体,是未来主要发展方向之一.在基础材料方面,除了传统的金属和介质之外,近年来研究了很多用于亚波长电磁学的新材料,包括半导体、液晶、相变材料、耐火材料、以石墨烯为代表的二维材料[106-109]等.这些材料为电磁功能器件的拓展奠定了重要基础.此外,采用类似于“材料基因组计划”的思路,基于麦克斯韦方程组建立亚波长结构基因数据库和软件平台,可为提高亚波长结构性能、降低研发周期和成本提供支撑.如图10所示,材料基因工程的思路可以直接应用到亚波长结构的设计,不同点只是计算和实验工具有所区别.
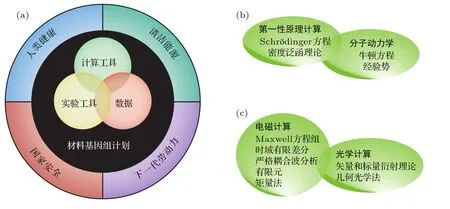
图10 亚波长结构基因计划 (a)“材料基因组计划”示意图;(b)传统材料的计算方法;(c)亚波长结构材料计算方法Fig.10.Subwavelength structured materials initiative:(a)Schematic of the materials initiative proposed by American National Science and Technology Council;(b)computational methods used for traditional materials;(c)computational methods for subwavelength structured materials.
[1]Luo X 2015 Sci.China:Phys.Mech.Astron.58 594201
[2]Lauterbach M A 2012 Opt.Nanoscopy 1 1
[3]Pendry J B 2000 Phys.Rev.Lett.85 3966
[4]Raguin D H,Morris G H 1993 Appl.Opt.32 1154
[5]Ribot C,Lalanne P,Lee M S L,Loiseaux B,Huignard J P 2007 J.Opt.Soc.Am.A 24 3819
[6]Luo X 2016 Front.Optoelectron.9 138
[7]Luo X G 2017 Sub-wavelength Electromagnetics(Vol.1) (Beijing:Science Press)pp4–5(in Chinese)[罗先刚2017亚波长电磁学(上册)(北京:科学出版社)第4—5页]
[8]Schurig D,Mock J J,Justice B J,Cummer S A,Pendry J B,Starr A F,Smith D R 2006 Science 314 977
[9]Xu T,Wang C,Du C,Luo X 2008 Opt.Express 16 4753
[10]Yu N,Genevet P,Kats M A,Aieta F,Tetienne J P, Capasso F,Gaburro Z 2011 Science 334 333
[11]Li Y,Li X,Pu M,Zhao Z,Ma X,Wang Y,Luo X 2016 Sci.Rep.6 19885
[12]Feng Q,Pu M,Hu C,Luo X 2012 Opt.Lett.37 2133
[13]Pu M,Zhao Z,Wang Y,Li X,Ma X,Hu C,Wang C, Huang C,Luo X 2015 Sci.Rep.5 9822
[14]Ebbesen T W,Lezec H J,Ghaemi H F,Thio T,Wol ffP A 1998 Nature 391 667
[15]Martin Moreno L,Garcia Vidal F J,Lezec H J,Pellerin K M,Thio T,Pendry J B,Ebbesen T W 2001 Phys. Rev.Lett.86 1114
[16]Genet C,Ebbesen T W 2007 Nature 445 39
[17]Liu H,Lalanne P 2008 Nature 452 728
[18]Lezec H J,Degiron A,Devaux E,Linke R A,Martin Moreno L,Garcia Vidal F J,Ebbesen T W 2002 Science 297 820
[19]Luo X,Pu M,Li X,Ma X 2017 Light Sci.Appl.6 e16276
[20]Dudley A,Lavery M P J,Padgett M J,Forbes A 2013 Opt.Photon.News 22 24
[21]Pu M,Li X,Ma X,Wang Y,Zhao Z,Wang C,Hu C, Gao P,Huang C,Ren H,Li X,Qin F,Gu M,Hong M, Luo X 2015 Sci.Adv.1 e1500396
[22]Li X,Pu M,Zhao Z,Ma X,Jin J,Wang Y,Gao P,Luo X 2016 Sci.Rep.6 20524
[23]Li X,Pu M,Wang Y,Ma X,Li Y,Gao H,Zhao Z,Gao P,Wang C,Luo X 2016 Adv.Opt.Mater.4 659
[24]Wang Y,Pu M,Zhang Z,Li X,Ma X,Zhao Z,Luo X 2015 Sci.Rep.5 17733
[25]Ozbay E 2006 Science 311 189
[26]Atwater H A 2007 Sci.Am.296 56
[27]Luo X,Ishihara T 2004 Opt.Express 12 3055
[28]Gao H,Shi H,Wang C,Du C,Luo X,Deng Q,Lü Y, Lin X,Yao H 2005 Opt.Express 13 10795
[29]Gramotnev D K,Bozhevolnyi S I 2010 Nat.Photon.4 83
[30]Yablonovitch E 1993 J.Opt.Soc.Am.B 10 283
[31]Russell P 2003 Science 299 358
[32]Aguirre C I,Reguera E,Stein A 2010 Adv.Funct.Mater. 20 2565
[33]Li Z Y,Meng Z M 2014 J.Mater.Chem.C 2 783
[34]Choi J H,No Y S,Hwang M S,Kwon S Y,Jeong K Y, Kwon S H,Yang J K,Park H G 2014 Appl.Phys.Lett. 104 91120
[35]Chen W D,Dong X Y,Chen Y,Zhu Q G,Wang N 2014 Acta Phys.Sin.63 154207(in Chinese)[陈卫东,董昕宇,陈颖,朱奇光,王宁2014物理学报63 154207]
[36]Huang X,Lai Y,Hang Z H,Zheng H,Chan C T 2011 Nat.Mater.10 582
[37]Rechtsman M C,Zeuner J M,Plotnik Y,Lumer Y, Podolsky D,Dreisow F,Nolte S,Segev M,Szameit A 2013 Nature 496 196
[38]Turner M D,Saba M,Zhang Q,Cumming B P,Schroder Turk G E,Gu M 2013 Nat.Photon.7 801
[39]Raman A P,Anoma M A,Zhu L,Rephaeli E,Fan S 2014 Nature 515 540
[40]Rybin M V,Filonov D S,Samusev K B,Belov P A, Kivshar Y S,Limonov M F 2015 Nat.Commun.6 10102
[41]Smith D,Padilla W,Vier D,Nemat Nasser S,Schultz S 2000 Phys.Rev.Lett.84 4184
[42]Pendry J B,Schurig D,Smith D R 2006 Science 312 1780
[43]Pendry J B,Aubry A,Smith D R,Maier S A 2012 Science 337 549
[44]Meinzer N,Barnes W L,Hooper I R 2014 Nat.Photon. 8 889
[45]Pu M,Ma X,Li X,Guo Y,Luo X 2017 J.Mater.Chem. C 5 4361
[46]Kamali S M,Arbabi A,Arbabi E,Horie Y,Faraon A 2016 Nat.Commun.7 11618
[47]Luo X,Pu M,Ma X,Li X 2015 Int.J.Antennas Propag. 2015 204127
[48]Wood R W 1902 Proc.R.Soc.Lond.18 269
[49]Hutley M C,Maystre D 1976 Opt.Commun.19 431
[50]Senior T 1981 IEEE Trans.Antennas Propag.29 826
[51]Li Y F,Qu S B,Xu Z 2014 Acta Phys.Sin.63 084103 (in Chinese)[李勇峰,屈绍波,徐卓 2014物理学报 63 084103]
[52]Yu N,Capasso F 2014 Nat.Mater.13 139
[53]Minovich A E,Miroshnichenko A E,Bykov A Y,Murzina T V,Neshev D N,Kivshar Y S 2015 Laser Photon. Rev.9 195
[54]Sun H 2016 Sci.China:Phys.Mech.Astron.59 614202
[55]Xu T,Wu Y K,Luo X,Guo L J 2010 Nat.Commun.1 59
[56]Hong M 2016 Sci.Bull.61 112
[57]Luo X,Ishihara T 2004 Appl.Phys.Lett.84 4780
[58]Choi M,Lee S H,Kim Y,Kang S B,Shin J,Kwak M H, Kang K Y,Lee Y H,Park N,Min B 2011 Nature 470 369
[59]Lalanne P,Astilean S,Chavel P,Cambril E,Launois H 1998 Opt.Lett.23 1081
[60]Smith D,Mock J,Starr A,Schurig D 2005 Phys.Rev. E 71 36609
[61]Pu M,Chen P,Wang C,Wang Y,Zhao Z,Hu C,Luo X 2013 AIP Adv.3 52136
[62]Khorasaninejad M,Chen W T,Devlin R C,Oh J,Zhu A Y,Capasso F 2016 Science 352 1190
[63]Arbabi A,Arbabi E,Kamali S M,Horie Y,Han S, Faraon A 2016 Nat.Commun.7 13682
[64]Luo X G,Xu T,Du C L,Wang C T 2008 China Patent ZL200710177752.5[2008-4-9](in Chinese)[罗先刚,徐挺,杜春雷,王长涛2008中国专利ZL200710177752.5[2008-4-9]]
[65]Zhao Z Y,Pu M B,Wang Y Q,Luo X G 2017 Opto-Elec.Eng.44 129(in Chinese)[赵泽宇,蒲明博,王彦钦,罗先刚2017光电工程44 129]
[66]Pu M,Chen P,Wang Y,Zhao Z,Huang C,Wang C,Ma X,Luo X 2013 Appl.Phys.Lett.102 131906
[67]Grady N K,Heyes J E,Chowdhury D R,Zeng Y,Reiten M T,Azad A K,Taylor A J,Dalvit D A R,Chen H T 2013 Science 340 1304
[68]Zheng G,Mühlenbernd H,Kenney M,Li G,Zhang S 2015 Nat.Nanotechnol.10 308
[69]Zhang L,Zhou P,Chen H,Lu H,Xie J,Deng L 2015 J. Opt.17 105105
[70]Zhang Z,Luo J,Song M,Yu H 2015 Appl.Phys.Lett. 107 241904
[71]Guo Y H,Pu M B,Ma X L,Li X,Luo X G 2017 Opto-Elec.Eng.44 3(in Chinese)[郭迎辉,蒲明博,马晓亮,李雄,罗先刚2017光电工程44 3]
[72]Ye D,Wang Z,Xu K,Li H,Huangfu J,Wang Z,Ran L 2013 Phys.Rev.Lett.111 187402
[73]Guo Y,Wang Y,Pu M,Zhao Z,Wu X,Ma X,Wang C, Yan L,Luo X 2015 Sci.Rep.5 8434
[74]Pu M,Hu C,Wang M,Huang C,Zhao Z,Wang C,Feng Q,Luo X 2011 Opt.Express 19 17413
[75]Rozanov K N 2000 IEEE Trans.Antennas Propag.48 1230
[76]Gustafsson M,Sjoberg D 2011 IEEE Trans.Antennas Propag.59 2196
[77]Lier E,Werner D H,Scarborough C P,Wu Q,Bossard J A 2011 Nat.Mater.10 216
[78]Chen P Y,Argyropoulos C,Alù A 2013 Phys.Rev.Lett. 111 233001
[79]Wang C,Gao P,Tao X,Zhao Z,Pu M,Chen P,Luo X 2013 Appl.Phys.Lett.103 31911
[80]Liu L,Gao P,Liu K,Kong W,Zhao Z,Pu M,Wang C, Luo X 2017 Mater.Horiz.4 290
[81]Fang N,Lee H,Sun C,Zhang X 2005 Science 308 534
[82]Maier S A,Kik P G,Atwater H A,Meltzer S,Harel E, Koel B E,Requicha A A G 2003 Nat.Mater.2 229
[83]Zijlstra P,Chon J W M,Gu M 2009 Nature 459 410
[84]Gao P,Yao N,Wang C,Zhao Z,Luo Y,Wang Y,Gao G,Liu K,Zhao C,Luo X 2015 Appl.Phys.Lett.106 93110
[85]Wang C T,Zhao Z Y,Gao P,Luo Y F,Luo X G 2016 Chin.Sci.Bull.61 585(in Chinese)[王长涛,赵泽宇,高平,罗云飞,罗先刚2016科学通报61 585]
[86]Zhao Z,Luo Y,Zhang W,Wang C,Gao P,Wang Y,Pu M,Yao N,Zhao C,Luo X 2015 Sci.Rep.5 15320
[87]Garcia Vidal F J,Martin Moreno L,Ebbesen T W, Kuipers L 2010 Rev.Mod.Phys.82 729
[88]Grzegorczyk T M,Nikku M,Chen X,Wu B I,Kong J A 2005 IEEE Trans.Microw.Theory Tech.53 1443
[89]Verslegers L,Catrysse P B,Yu Z,White J S,Barnard E S,Brongersma M L,Fan S 2009 Nano Lett.9 235
[90]Goh X M,Lin L,Roberts A 2010 Opt.Express 18 11683
[91]Tang D,Wang C,Zhao Z,Wang Y,Pu M,Li X,Gao P, Luo X 2015 Laser Photon.Rev.9 713
[92]Ma X,Pu M,Li X,Huang C,Wang Y,Pan W,Zhao B, Cui J,Wang C,Zhao Z,Luo X 2015 Sci.Rep.5 10365
[93]Zhao Z,Pu M,Gao H,Jin J,Li X,Ma X,Wang Y,Gao P,Luo X 2015 Sci.Rep.5 15781
[94]Li X,Ren H,Chen X,Liu J,Li Q,Li C,Xue G,Jia J, Cao L,Sahu A,Hu B,Wang Y,Jin G,Gu M 2015 Nat. Commun.6 6984
[95]Li X,Chen L,Li Y,Zhang X,Pu M,Zhao Z,Ma X, Wang Y,Hong M,Luo X 2016 Sci.Adv.2 e1601102
[96]Jin J,Pu M,Wang Y,Li X,Ma X,Luo J,Zhao Z,Gao P,Luo X 2017 Adv.Mater.Technol.2 1600201
[97]Ni X,Wong Z J,Mrejen M,Wang Y,Zhang X 2015 Science 349 1310
[98]Qu Y,Li Q,Gong H,Du K,Bai S,Zhao D,Ye H,Qiu M 2016 Adv.Opt.Mater.4 480
[99]Pu M,Hu C,Huang C,Wang C,Zhao Z,Wang Y,Luo X 2013 Opt.Express 21 992
[100]Bossard J A,Lin L,Yun S,Liu L,Werner D H,Mayer T S 2014 ACS Nano 8 1517
[101]Pu M,Feng Q,Wang M,Hu C,Huang C,Ma X,Zhao Z,Wang C,Luo X 2012 Opt.Express 20 2246
[102]Li S,Duan Q,Li S,Yin Q,Lu W,Li L,Gu B,Hou B, Wen W 2015 Appl.Phys.Lett.107 181112
[103]Li W,Guler U,Kinsey N,Naik G V,Boltasseva A,Guan J,Shalaev V M,Kildishev A V 2014 Adv.Mater.26 7959
[104]Kohiyama A,Shimizu M,Yugami H 2016 Appl.Phys. Express 9 112302
[105]Poddubny A,Iorsh I,Belov P,Kivshar Y 2013 Nat.Photon.7 948
[106]Ho ff man A J,Alekseyev L,Howard S S,Franz K J, Wasserman D,Podolskiy V A,Narimanov E E,Sivco D L,Gmachl C 2007 Nat.Mater.6 946
[107]Naik G V,Shalaev V M,Boltasseva A 2013 Adv.Mater. 25 3264
[108]Guler U,Boltasseva A,Shalaev V M 2014 Science 344 263
[109]Wang D,Zhang L,Gu Y,Mehmood M Q,Gong Y, Srivastava A,Jian L,Venkatesan T,Qiu C W,Hong M 2015 Sci.Rep.5 15020
PACS:41.20.Jb,42.25.—p,42.70.—a,73.20.Mf DOI:10.7498/aps.66.144101
Subwavelength electromagnetics below the di ff raction limit∗
Pu Ming-Bo Wang Chang-Tao Wang Yan-Qin Luo Xian-Gang†
(State Key Laboratory of Optical Technologies on Nano-Fabrication and Micro-Engineering,Institute of Optics and Electronics, Chinese Academy of Sciences,Chengdu 610209,China)
21 April 2017;revised manuscript
19 May 2017)
As a fundamental property of waves,di ff raction plays an important role in many physical problems.However, di ff raction makes waves in free space unable to be focused into an arbitrarily small space,setting a fundamental limit (the so-called di ff raction limit)to applications such as imaging,lithography,optical recording and waveguiding,etc. Although the di ff raction e ff ect can be suppressed by increasing the refractive index of the surrounding medium in which the electromagnetic and optical waves propagate,such a technology is restricted by the fact that natural medium has a limited refractive index.In the past decades,surface plasmon polaritons(SPPs)have received special attention, owing to its ability to break through the di ff raction limit by shrinking the e ff ective wavelength in the form of collective excitation of free electrons.By combining the short wavelength property of SPPs and subwavelength structure in the two-dimensional space,many exotic optical e ff ects,such as extraordinary light transmission and optical spin Hall e ff ect have been discovered and utilized to realize functionalities that control the electromagnetic characteristics(amplitudes, phases,and polarizations etc.)on demand.Based on SPPs and arti fi cial subwavelength structures,a new discipline called subwavelength electromagnetics emerged in recent years,thus opening a door for the next-generation integrated and miniaturized electromagnetic and optical devices and systems.
In this paper,we review the theories and methods used to break through the di ff raction limit by brie fl y introducing the history from the viewpoint of electromagnetic optics.It is shown that by constructing plasmonic metamaterials and metasurfaces on a subwavelength scale,one can realize the localized phase modulation and broadband dispersion engineering,which could surpass many limits of traditional theory and lay the basis of high-performance electromagnetic and optical functional devices.For instance,by constructing gradient phase on the metasurfaces,the traditional laws of re fl ection and refraction can be rewritten,while the electromagnetic and geometric shapes could be decoupled,both of which are essential for realizing the planar and conformal lenses and other functional devices.At the end of this paper, we discuss the future development trends of subwavelength electromagnetics.Based on the fact that di ff erent concepts, such as plasmonics,metamaterials and photonic crystals,are closely related to each other on a subwavelength scale, we think,the future advancements and even revolutions in subwavelength electromagnetics may rise from the in-depth intersection of physical,chemical and even biological areas.Additionally,we envision that the material genome initiative can be borrowed to promote the information exchange between di ff erent engineering and scienti fi c teams and to enable the fast designing and implementing of subwavelength structured materials.
di ff raction limit,surface plasmon,metamaterials,metasurfaces
:41.20.Jb,42.25.—p,42.70.—a,73.20.Mf
10.7498/aps.66.144101
∗国家重点基础研究发展计划(批准号:2013CBA01700)和国家自然科学基金(批准号:61622508,61575201)资助的课题.
†通信作者.E-mail:lxg@ioe.ac.cn
©2017中国物理学会Chinese Physical Society
http://wulixb.iphy.ac.cn
*Project supported by the National Basic Research Program of China(Grant No.2013CBA01700)and the National Natural Science Foundation of China(Grant Nos.61622508,61575201).
†Corresponding author.E-mail:lxg@ioe.ac.cn
