常见动态混凝土材料模型基本力学特征对比分析

陈 林，颜泽峰

（湖南科技大学 土木工程学院，湖南 湘潭 411201）

常见动态混凝土材料模型基本力学特征对比分析

陈 林，颜泽峰

（湖南科技大学 土木工程学院，湖南 湘潭 411201）

材料本构模型的选择和使用，一直是制约混凝土构件动态损伤模拟技术发展的重要因素之一。基于通用有限元软件LS-DYNA，对其中2种常用的混凝土材料模型（混凝土损伤模型和混凝土连续面盖帽模型）的基本力学行为进行了对比分析。研究结果表明，混凝土损伤模型和连续面盖帽模型在基本应力应变关系、网格敏感性和应变率效应等方面均存在明显的差异。因此，采用这些材料模型进行有限元分析时，必须经过严格的试验验证，特别是在模型校正和后续参数分析时，应采用相同或相近的网格尺寸，以消除网格敏感性的影响。

混凝土损伤模型；混凝土连续面盖帽模型；静力压缩与拉伸；网格敏感性；应变率效应

0 引言

在爆炸、冲击和车辆碰撞等结构动力分析领域，由于试验难度和成本较高，研究者们广泛采用有限元方法对该类问题进行分析。其中最广泛使用的通用商业有限元软件是Livermore Software Technology Corporation开发的LS-DYNA。该软件具有数量庞大的单元模型、材料模型和接触类型等，适用于各类复杂工况的数值模拟[1]。

混凝土构件在冲击动力作用下的反应十分复杂，采用有限元模拟的难度较大，特别是当构件倾向于剪切破坏时。混凝土材料模型的选择与使用是模拟成败的关键之一。到目前为止，众多研究者开发出了一系列的针对混凝土这类脆性材料的本构模型，LS-DYNA软件平台也已引入多种这类模型。对于中低速冲击作用下混凝土力学行为的模拟，最常使用的2种模型是K&C混凝土损伤模型第三次改进版（LS-DYNA材料模型编号#72R3）[2-3]和连续面盖帽模型（continuous surface cap model，CSCM）（LS-DYNA材料模型编号#159）[4-5]。这2种模型在LS-DYNA平台中均具有默认参数和用户自定义参数2种模式。使用默认参数模式时，用户只需输入极少参数，如混凝土密度和单轴抗压强度等；用户自定义参数模式的优点在于用户可以根据试验数据对模型参数作进一步的校正，从而提高模拟精度。截至目前，还少有人对以上2种典型混凝土材料模型的基本力学行为（包括全过程拉压应力应变关系、网格敏感性和应变率效应等）进行仔细的研究。有鉴于此，本文基于LS-DYNA软件平台对K&C混凝土损伤模型和连续面盖帽模型的基本力学行为进行对比分析，以期为混凝土构件在冲击作用下的仿真模拟提供参考。

1 材料模型概述

1.1 混凝土损伤模型

混凝土损伤模型最初是为显式有限元程序DYNA3D开发，用以解决爆炸荷载作用下混凝土材料的冲击模拟问题。该材料模型经过了一系列的改进，其中第三次改进版增加了模型内部参数自动生成功能，大大提高了模型使用的方便性。

混凝土损伤模型属于三应力不变量模型（I1,J2,J3），且考虑了混凝土材料的硬化、率相关性及损伤软化等特征。该模型采用3个独立的强度面来描述混凝土的力学行为，即初始屈服面、最大强度失效面以及残余强度面。混凝土损伤模型要求用户根据情况选择任意、合理的应变率效应模型。一般情况下可采用LS-DYNA用户手册建议的Malvar和Crawford混凝土应变率模型[6]，即

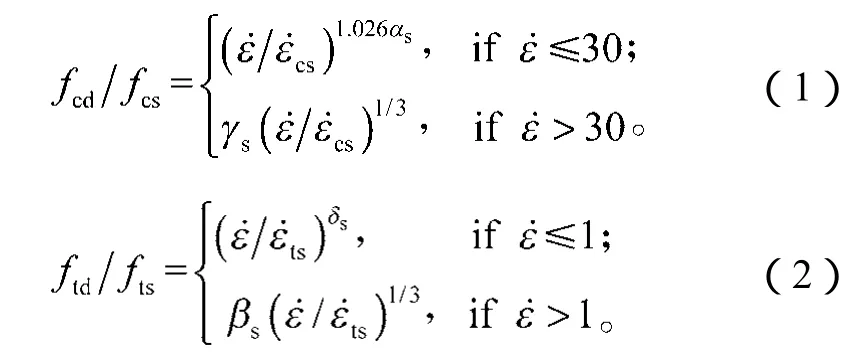
式（1）～（2）中：fcd,fcs分别为混凝土的动态和静态抗压强度，MPa；

ftd,fts分别为混凝土的动态和静态抗拉强度，MPa；

αs,γs,δs,βs为参数，且

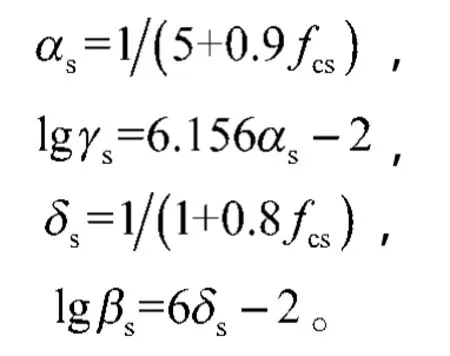
1.2 混凝土连续面盖帽模型

混凝土连续面盖帽模型（CSCM）由美国联邦公路管理署组织开发，用来模拟路侧混凝土类防护结构在车辆碰撞下的力学行为。该模型采用光滑曲面连接剪切屈服面和强化盖帽面。屈服面在偏平面上的投影形状由Willam-Warnke模型表述，而材料所经历的应力和应变历史决定了强化盖帽面的位置和大小。该模型考虑了材料的硬化、损伤以及率相关性，目前在钢筋混凝土结构低速冲击领域应用广泛。

混凝土连续面盖帽模型的应变率效应采用黏塑性算法，如公式（3）～（4）所示，断裂能、材料强度等与应变率的关系，取决于内部参数的取值。

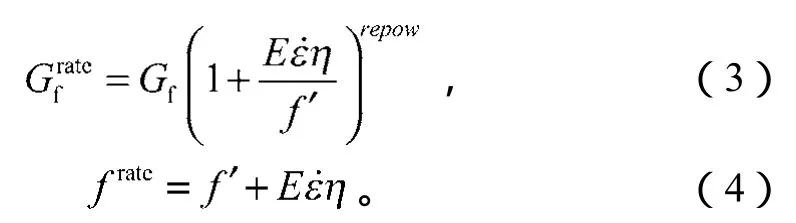
frate和f′分别为考虑和不考虑应变率效应的材料屈服强度；

E为材料弹性模量；

η为有效流动性系数。

由式（3）和（4）可知，参数repow其实已定义了断裂能的动力增大系数DIFFE与强度的动力增大系数DIFS之间的关系，即

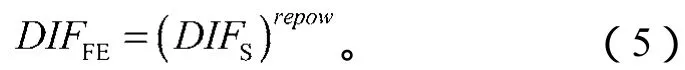
事实上，关于断裂能动力增大系数与强度动力增大系数间的关系目前仍存在分歧[7]。一些试验结果表明，随着应变率的增大，材料的最大破坏应变与抗拉强度同比例增大，从而使得repow=2；但另一些试验数据则得到断裂能保持恒定的结论，即repow=0。在LS-DYNA中repow默认值取上述2与0的中间值1，即断裂能与强度随应变率增长的速率相等。

2 基本力学行为分析

为了对以上2种常用混凝土材料模型的力学行为有进一步的了解，本章对默认参数下2种材料模型的单轴压缩和拉伸行为进行模拟分析，其中混凝土材料抗压强度值取25.4 MPa。

2.1 单个单元单轴静力压缩与拉伸分析

单元类型采用3D实体8节点单元，单元相邻两个侧面施加对称约束，单元底面施加竖向约束。采用位移加载的方式，对单元顶部4个节点施加等量的竖向位移，从而保证单元处于单轴受力状态，单元尺寸分别取100, 50, 25, 10 mm。采用动态显式分析方法，但关闭材料模型内部所有与应变率相关的参数；同时，加载速率设置为足够小，从而确保速率效应不会对材料力学行为产生影响。

图1～2分别为采用混凝土损伤模型和连续面盖帽模型分析得到的应力-应变关系曲线。

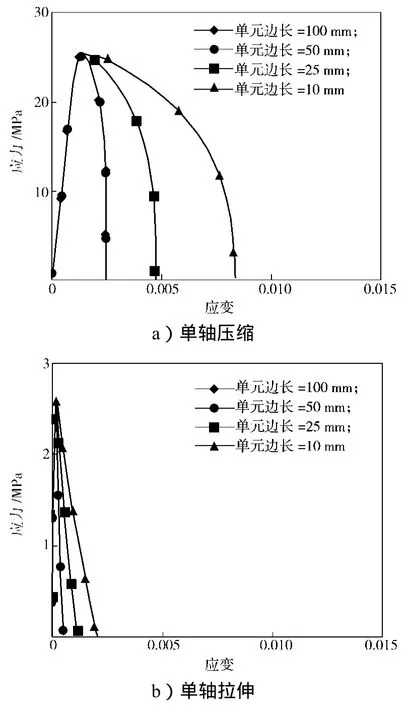
图1 混凝土损伤模型的单个单元应力-应变曲线Fig. 1 Stress-strain curves of single elements of concrete damage model

由图1～2可知，随着单元尺寸的减小，单元应力-应变曲线趋于饱满，说明单元延性增加。这一点实际上与2种材料内部采用的恒定断裂能原理相吻合[2,5]。当单元尺寸逐渐变小至25 mm及以下时，混凝土损伤模型的应力-应变关系趋于稳定，但连续面盖帽模型则不会。从图还可以看出，在同样单元尺寸条件下，采用连续面盖帽模型的单元整体上比采用混凝土损伤模型的单元表现出更大的延性。

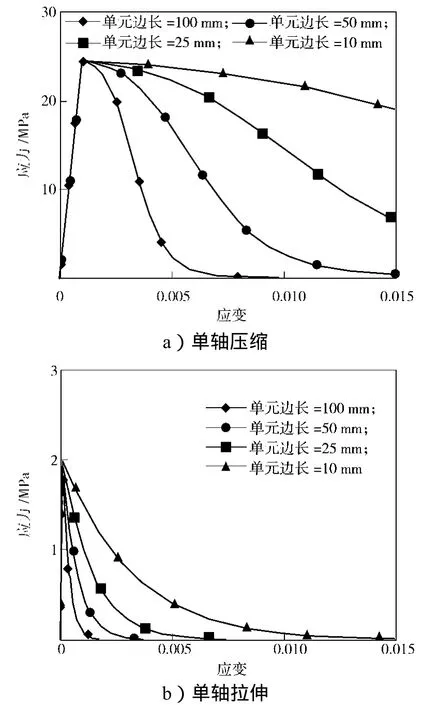
图2 连续面盖帽模型的单个单元应力-应变曲线Fig. 2 Stress-strain curves of single elements of continuous surface cap model

2.2 网格敏感性分析

建立一个边长为100 mm的立方体，采用4种网格尺寸对其进行划分，即100, 50, 25, 10 mm，如图3所示。

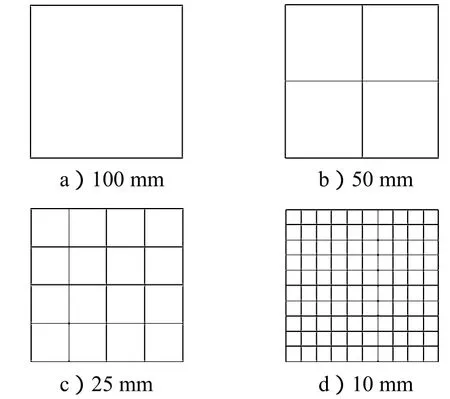
图3 立方体的网格划分尺寸示意图Fig. 3 Sketch maps of the mesh size for cubes

对该立方体采用与2.1节中单个单元分析类似的约束和加载方法，用混凝土损伤模型和连续面盖帽模型分析得到的立方体平均应力-应变关系，如图4～5所示。由图可知，在单轴受压状态下2种材料模型均表现出较强的网格依耐性；但是当网格划分尺寸小于或等于25 mm时，混凝土损伤模型对应的应力-应变关系趋于稳定，而连续面盖帽模型则不会，这与单个单元分析结果相似。当立方体单轴受拉时，2种材料模型对应的应力-应变关系基本上与网格尺寸大小无关，不过当网格尺寸小至10 mm时，采用混凝土损伤模型的立方体突然表现出较强的脆性。

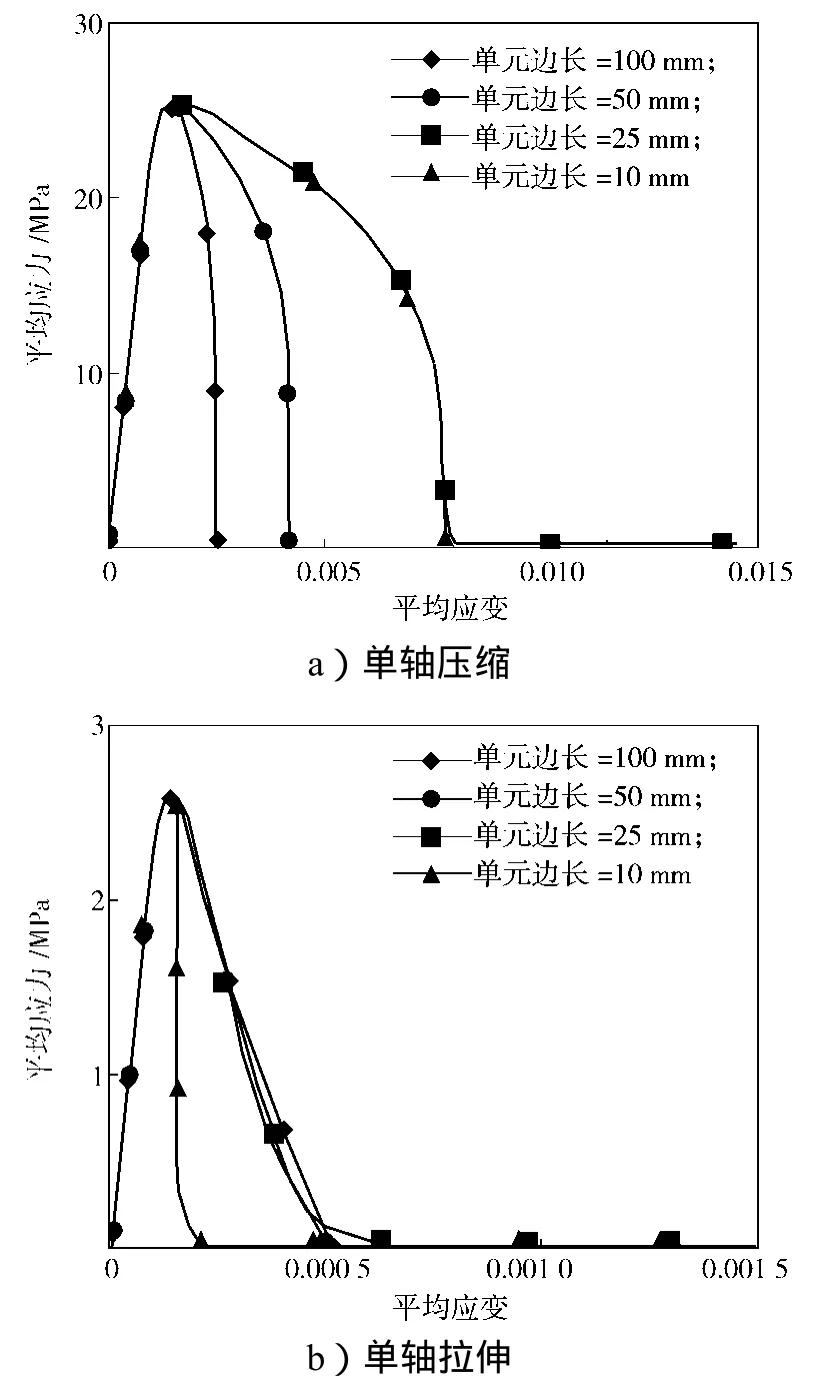
图4 混凝土损伤模型的立方体平均应力-应变曲线Fig. 4 Average stress-strain curves of cubes of concrete damage model

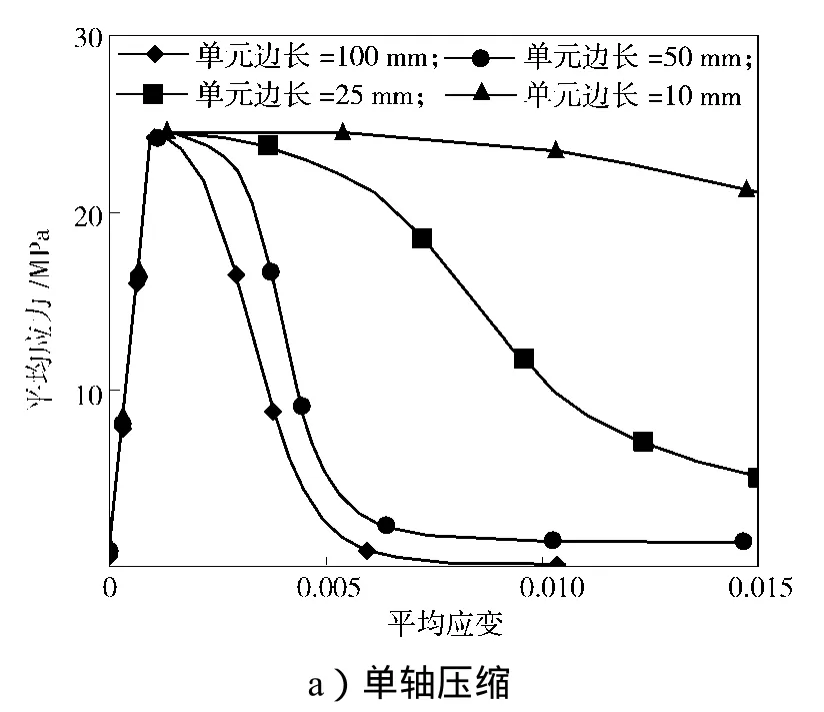
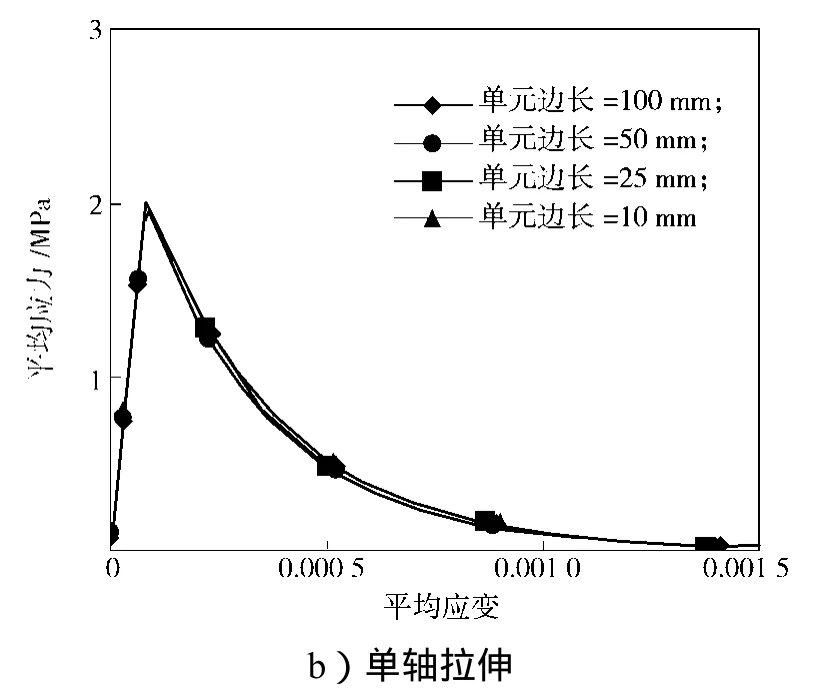
图5 连续面盖帽模型的立方体平均应力-应变曲线Fig. 5 Average stress-strain curves of cubes of continuous surface cap model

2.3 应变率效应分析

为了了解2种材料模型对应的应变率效应，对边长为25 mm的单个立方体单元，分别采用静力（指加载速率非常小），应变率为0.1/s、1.0/s和10.0/s的4种加载速率，施加单轴压缩和拉伸荷载，得到不同应变率下的应力-应变曲线，如图6～7所示。

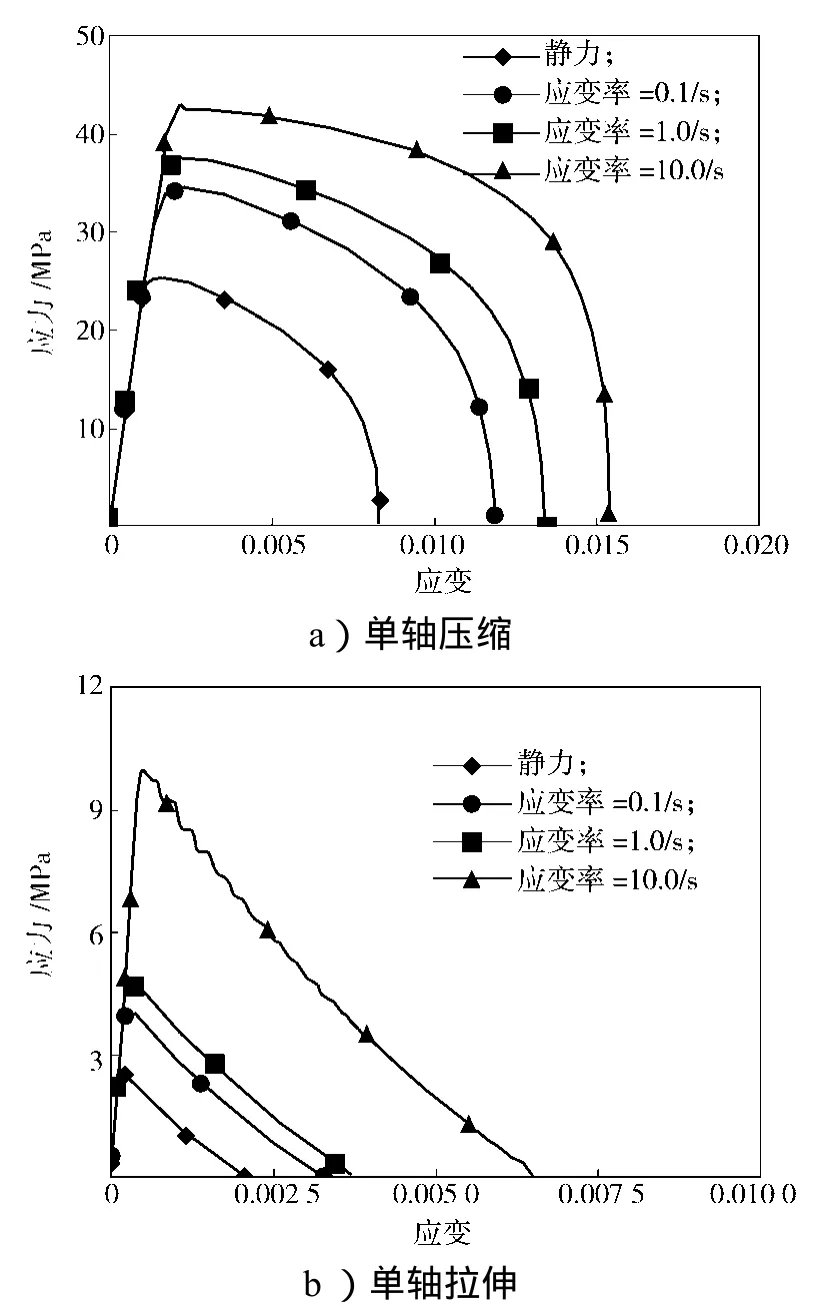
图6 混凝土损伤模型应变率效应Fig. 6 Strain rate effect ofconcrete damage models

由图6～7可知，混凝土损伤模型对应的应变率增大效应（即Malvar和Crawford混凝土应变率模型）明显高于连续面盖帽模型，特别是在混凝土单轴拉伸时。在采用默认内置参数的情况下，随着加载速率的提高，2种材料模型对应的材料强度均得到提高。不同的是，随着加载速率的提高，混凝土损伤模型破坏应变的增长速度与强度的增长速度基本相当，而连续面盖帽模型的破坏应变则基本保持不变。

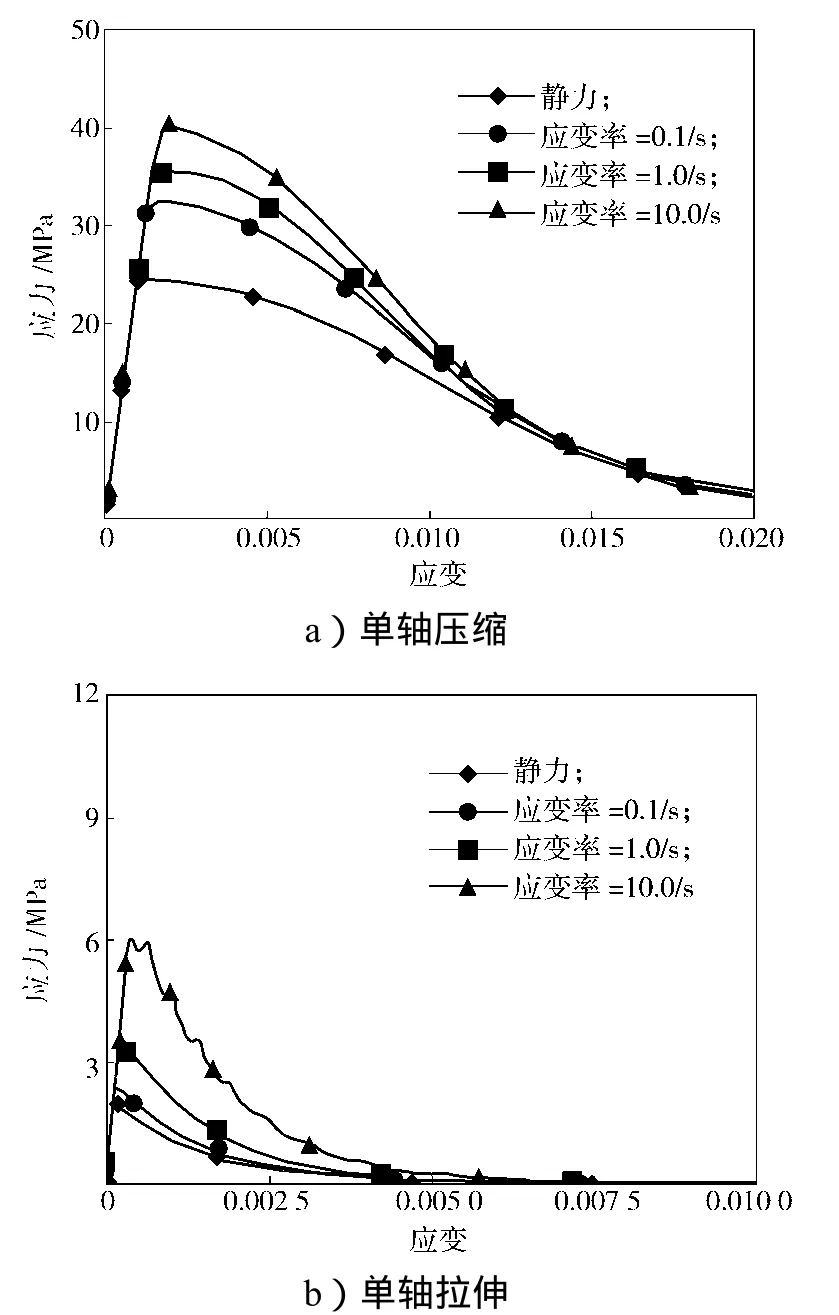
图7 连续面盖帽模型应变率效应Fig. 7 Strain rate effect ofcontinuous surface cap model

3 结语

综上所述，无论是静力还是动力力学行为，混凝土损伤模型与连续面盖帽模型都具有明显的差异。这种差异可能进一步导致在模拟钢筋混凝土构件时产生明显不同的结果。整体而言，2种材料模型均具有明显的网格依赖性。因此，建议在使用任一材料模型时必须经过严格的试验验证，并且在模型校正和后续参数分析时，采用相同或相近的网格划分，以消除网格尺寸的影响。

[1] Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual[EB/OL]. [2017-01-05]. http://www.dynasupport.com/manuals/ls-dyna-manuals/LSDYNA_Keyword_Manual_971_Rev5-beta.pdf.

[2] MAGALLANES J M，WU Y，MALVAR L J，et al.Recent Improvements to Release III of the K&C Concrete Model[EB/OL]. [2017-01-05]. http://www.dynalook.com/international-conf-2010/Simulation-1-4.pdf.

[3] MALVAR L J，CRAWFORD J E，WESEVICH J W，et al. A Plasticity Concrete Material Model for DYNA3D[J].International Journal of Impact Engineering，1997，19(9/10)：847-873.

[4] MURRAY Y D. Users Manual for LS-DYNA Concrete Material Model 159[M]. Colorado Springs：APTEK，2007：1-77.

[5] MURRAY Y D，ABU-ODEH A Y，BLIGH R P.Evaluation of LS-DYNA Concrete Material Model 159[M]. Colorado Springs：APTEK，2007：1-190.

[6] MALVAR L J，CRAWFORD J E. Dynamic Increase Factors for Concrete[EB/OL]. [2017-01-05]. http://dtic.mil/get-tr-doc/pdf?AD=ADA500715&Location=U2&doc=GetTRDoc.pdf.

[7] BRARA A，KLEPACZKO J R. Fracture Energy of Concrete at High Loading Rates in Tension[J].International Journal of Impact Engineering，2007，34(3)：424-435

（责任编辑：邓光辉）

Comparative Analysis of the Basic Mechanical Characteristics of the Commonly-Used Dynamic Concrete Material Models

CHEN Lin，YAN Zefeng
（School of Civil Engineering，Hunan University of Science and Technology，Xiangtan Hunan 411201，China）

The selection and application of the material constitutive model has always been one of the most important factors that restrict the development of the damage simulation of concrete members under dynamic loading.Based on the general finite element software LS-DYNA, a comparison and an analysis hare been made of the basic mechanical behavior of two kinds of commonly-used concrete material models (concrete damage model and continuous surface cap model). The experimental results show that there are signi fi cant differences in the basic stressstrain relationship, grid sensitivity and strain rate effect between the concrete damage model and continuous surface cap model. Hence, there should be a strict experimental veri fi cation in the process of the fi nite element analysis of the material model; speci fi cally, in order to eliminate the effects of the grid sensitivity, the same or similar grid size should be used for the analysis of the model validation process and follow-up parameters.

concrete damage model；continuous surface cap model；static compression and tension；grid sensitivity；strain rate effect

TU312

：A

：1673-9833(2017)03-0001-05

10.3969/j.issn.1673-9833.2017.03.001

2017-01-15

国家自然科学青年基金资助项目（51608191），湖南省教育厅优秀青年基金资助项目（16B090）

陈 林（1986-），男，湖南怀化人，湖南科技大学讲师，博士，主要研究方向为工程结构抗撞抗冲击，E-mail：civil-chenlin@hnust.edu.cn