高考易错题自测卷——导数

陕西 侯有岐

高考易错题自测卷
——导数

陕西 侯有岐

一、选择题

1．函数y＝（x＋1）2（x－1）在x＝1处的导数等于 （ ）

A．1 B．2 C．3 D．4

2．若曲线y＝x4－x的一条切线l与直线x＋3y＋1＝0垂直，则直线l的方程为 （ ）

A．x－3y－3＝0 B．3x－y－3＝0

C．3x－y－1＝0 D．x－3y－1＝0

4．过点（－1，0）作曲线y＝x2＋x＋1的切线，则其中一条切线方程为 （ ）

A．2x＋y＋2＝0 B．3x－y＋3＝0

C．x＋y＋1＝0 D．x－y＋1＝0

5．函数f（x）＝（x2－1）3＋1的极值点为 （ ）

A．x＝1 B．x＝－1

C．x＝1或x＝0或x＝－1 D．x＝0

A．k＞1 B．k≥1

C．｜k｜＞1 D．｜k｜≥1

7．函数y＝ln（2－3x）的单调区间为 （ ）

9．已知函数f（x）＝x3＋ax2＋bx＋a2在x＝1处有极值10，则f（2）＝ （ ）

A．11 B．18

C．11或18 D．17或3

10．已知函数f（x）＝ax·x2＋cosx，则其导数是（ ）

A．x（ax－1x2＋2ax）－sinx

B．x（ax－1x2＋2ax）＋sinx

C．ax（x2lna＋2x）－sinx

D．ax（x2lna＋2x）＋sinx

11．已知函数f（x）的导函数为f′（x），且满足f（x）＝2xf′（e）＋lnx，则f′（e）＝ （ ）

A．1 B．－1 C．－e－1D．－e

12．函数y＝（1＋cos2x）2的导数是 （ ）

A．－2sin2x（1＋cos2x）

B．2sin2x（1＋cos2x）

C．－4sin2x（1＋cos2x）

D．4sin2x（1＋cos2x）

二、填空题

13．若曲线f（x）＝acosx与曲线g（x）＝x2＋bx＋1在交点（0，m）处有公切线，则a＋b＝________．

15．已知曲线y＝x3＋x＋1，则①过点P（1，3）的切线方程为_____________；②在点P（1，3）处的切线方程为______ ________．

16．下列关于函数的说法中，正确的有________（写出所有正确命题的序号）．

①若f′（x0）＝0，则f（x0）为f（x）的极值点；

②在闭区间［a，b］上，极大值中最大的就是最大值；

③若f（x）的极大值为f（x1），f（x）的极小值为f（x2），则f（x1）＞f（x2）；

④有的函数有可能有两个最小值；

⑤已知函数f（x）＝ex，对于f（x）定义域内的任意一个x1都存在唯一一个值x2，使f（x1）f（x2）＝1成立．

三、解答题

17．已知函数f（x）＝ax3＋x2－x（a∈R）．

（1）若f（x）在（2，＋∞）上是单调递增的，求实数a的取值范围；

（2）若f（x）在（2，＋∞）上存在单调递增区间，求实数a的取值范围．

（1）若函数g（x）＝f（x）＋2k有两个不同的零点，求实数k的取值范围；

（2）若函数g（x）＝f（x）＋2k恰有一个零点，求实数k的取值范围．

【参考答案与提示】

1．D 【解析】因为y＝（x＋1）2（x－1），所以y′＝2（x＋1）（x－1）＋（x＋1）2＝3x2＋2x－1，所以，在x＝1处的导数为4，故选D．

【易错警示】对于某一点的导数的求解，要特别注意复合函数的求导法则，避免出错的有效途径是将其展开，利用基本导数公式来解决有关问题．

2．B 【解析】与直线x＋3y＋1＝0垂直的直线l为3x－y＋m＝0，即y＝x4－x在某一点的导数为3，而y′＝4x3－1，由4x3－1＝3，解得x＝1，所以y＝x4－x在（1，0）处导数为3，此点的切线为3x－y－3＝0，故选B．

【易错警示】理解导数概念容易忽视导数的某些实际背景，解决导数中有关切线问题，要明确导数的几何意义，以及某一点处的导数的定义，然后再解才不至于出错，因此要加强对导数概念的理解．

3．D 【解析】因为f′（x）－f（x）＝xex，

【易错警示】抽象函数的导数问题在高考中常考常新，可谓变化多端，解题关键在于构造函数，这就要求我们熟悉导数的四则运算和复合运算法则，结合问题的外形结构特征与导数法则的结构特征进行合理构造．

【易错警示】正确理解导数的几何意义是解答本题的关键，切线的斜率k应是在切点处的导数，而点（－1，0）不在曲线上（即使在曲线上，也应先判断其是否为切点），更不是切点．故本题应先设切点，再求斜率，写出切线方程．

5．D 【解析】由f′（x）＝6x（x2－1）2＝6x（x＋1）2·（x－1）2，可知

所以只有x＝0是f（x）的极值点．故选D．

【易错警示】本题易错选C，错解是因为误认为导数为0的点是极值点，而没有代入检验．事实上，f′（x0）＝0是f（x）在点x0处取得极值的必要不充分条件，导数为0的点只是函数存在极值的可能点，若它的两侧导数异号，它才是函数的极值点；若它的两侧导数同号，则不为极值点，所以在求得导数为0的点后，还要进行检验，否则容易出错．

【易错警示】当f（x）不含参数时，可通过解不等式f′（x）＞0（或f′（x）＜0）直接得到单调递增（或递减）区间．而已知函数的单调性，求参数的取值范围时，应用条件f′（x）≥0（或f′（x）≤0），x∈（a，b）恒成立，解出参数的取值范围，应注意参数的取值是f′（x）不恒等于0的参数的范围．

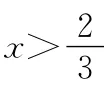
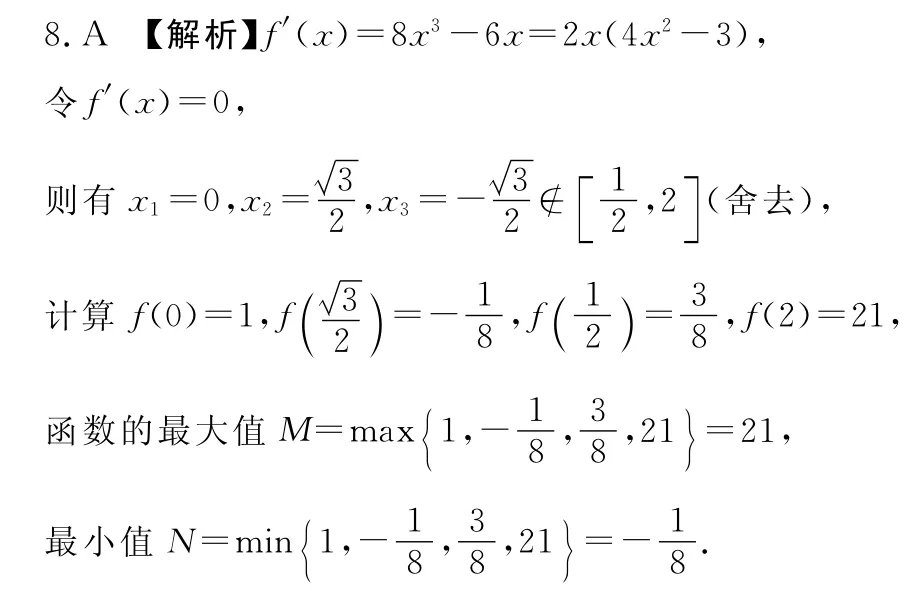
故选A．

【易错警示】求函数的最大值和最小值时，一定要考虑区间端点的函数值，但是，在通常情况下不必确定极大值和极小值，而只需把所有极大值和极小值与区间端点值的函数值计算出来，然后比较大小即可．

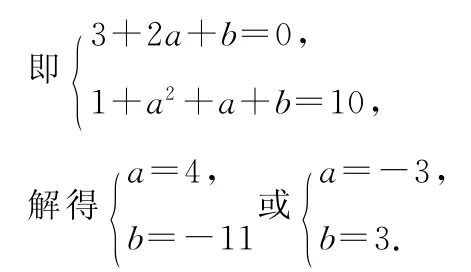
当a＝4，b＝－11时，f′（x）＝（3x＋11）（x－1），所以当x＞1时，f′（x）＞0；

当－11＜x＜1时，f′（x）＜0，此时f（x）在x＝1处有极值，所以f（2）＝18．

当a＝－3，b＝3时，f′（x）＝3（x－1）2，所以当x＞1时，f′（x）＞0；

当x＜1时，f′（x）＞0，又f（x）在x＝1处连续，因此f（x）在R上是增函数，所以f（x）在x＝1处无极值，因此a＝－3，b＝3时不合题意，应舍去．所以f（2）＝18．故选B．

【易错警示】f′（x0）＝0是f（x）在x＝x0处有极值的必要不充分条件．若x＝x0是f′（x）＝0的偶次方根，则x0不是f（x）的极值点．

10．C 【解析】因为f（x）＝ax·x2＋cosx，所以f′（x）＝（ax·x2）′＋（cosx）′＝axlna·x2＋2x·ax－sinx＝ ax（x2lna＋2x）－sinx．故选C．

【易错警示】导数的概念与运算是导数的基础，但往往因为对公式的结构规律或法则记忆不正确而出错，如本题中易将y＝ax与y＝xn的求导法则相混淆，求cosx的导数时易漏掉负号，导致结果出错．

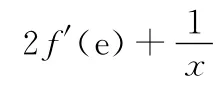
【易错警示】f′（x0）与f′（x）的关系是：f′（x0）是一个确定的数值，而f′（x）是一个函数；联系是f′（x0）是导函数f′（x）在x＝x0处的函数值．本题求导时，要注意已知式中的f′（e），由于f′（e）是一个常数，所以［f′（e）］′＝0．

12．C 【解析】设y＝u2，u＝1＋cos2x，则y′x＝y′u· u′x＝2u（1＋cos2x）′＝2u（－sin2x）（2x）′＝2u（－sin2x）· 2＝－4sin2x（1＋cos2x）．故选C．

【易错警示】复合函数求导时，选择中间变量是关键，必须正确分析复合函数的复合层次，然后从外向里逐层求导，求导后，要把中间变量转换成自变量的函数．易错点是由于在复合函数求导时，复合过程划分不彻底产生的，这里2x与x系数不一样，也是一个复合过程．

13．1【解析】因为f（x）＝acosx，g（x）＝x2＋bx＋1，所以f′（x）＝－asinx，g′（x）＝2x＋b，依题意有f′（0）＝g′（0），所以－asin0＝2×0＋bb＝0．

由于点（0，m）同时都在曲线f（x）与g（x）上，所以m＝f（0）＝g（0），即m＝acos0＝02＋b×0＋1m＝a＝1，

所以a＋b＝1＋0＝1．

【易错警示】求解本题易忽视切点在曲线上的隐含条件致错．在由f′（0）＝g′（0）得到b＝0，就应想到切线的切点必在原两函数的图象上，这样就有m＝f（0）＝g（0），这是解决本题的关键．

解得－1＜b＜3，

即实数b的取值范围为（－1，3）．

【易错警示】利用导数研究方程解的问题的一般思路是：（1）将问题转化为函数的零点问题，进而转化为函数的图象与x轴（或y＝k）在该区间上的交点问题；（2）利用导数研究出函数在该区间上单调性、极值（最值）、端点值等性质，进而结合图象求解．本题学生不会将方程解的问题转化为函数的零点问题，再运用导数工具结合图象求解．

15．①4x－y－1＝0或7x－4y＋5＝0②4x－y－1＝0

综上所述，①的答案为4x－y－1＝0或7x－4y＋5＝0；②的答案为4x－y－1＝0．

【易错警示】在确定曲线在某点处的切线方程时，一定要先确定此点是否在曲线上，若此点在曲线上，且求曲线在该点处的切线，那么曲线在该点处切线斜率即为该点的导数值，此时切线方程唯一；若此点不在曲线上，或此点在曲线上，但求过该点的切线方程时，则需按照上述方法，即应先设切点，再求斜率，然后求出直线方程，此时方程一般情况下不唯一．

16．⑤ 【解析】①错．导数为0的点仅是该点为极值点的必要条件，其充分条件是这点两侧的导数异号；

②错．闭区间上的极大值不一定是最大值，最大值有可能在区间端点处取得；

③错．极大值与极小值之间无确定的关系，即一个函数的极大值未必大于极小值；

④错．函数如果有最小值，必然是唯一的，否则就没有最小值；

⑤对．因为函数f（x）＝ex是R上的单调递增函数，只要x1与x2互为相反数必有f（x1）f（x2）＝1成立．

【易错警示】弄清函数的极值与最值的概念是正确解决本题的关键．

依题意，得3a≥g（x）max，即a≥0．

而当a＝0时，f′（x）＝2x－1在（2，＋∞）上恒有f′（x）＞0，满足题意．

所以，实数a的取值范围为［0，＋∞）．

（2）由于f（x）在（2，＋∞）上存在单调递增区间，所以存在3a≥g（x）成立，

【易错警示】由函数的单调性、极值等问题求解参数的取值范围是高考命题的一个重点．解决此类问题的关键在于正确理解单调性、极值的概念和其求解、判断的方法．要注意以下细节问题：（1）f′（x）＞0（＜0）（x∈（a，b））是f（x）在（a，b）上单调递增（减）的充分不必要条件．实际上，可导函数f（x）在（a，b）上为单调递增（减）函数的充要条件为：对于任意x∈（a，b），有f′（x）≥0（≤0）且f′（x）在（a，b）的任意子区间上都不恒为0．因而这类题求出参数范围后，应对“＝”成立的值进行检验，看是否符合题意；（2）解题中对“恒成立、能成立、恰成立”等概念区分不清也易致错．

当x→－∞时，y→0且x＜0时，y＝g（x）＝（2x－x2）· ex＜0．

（1）若函数g（x）＝f（x）＋2k有两个不同的零点，

（作者单位：陕西省汉中市四○五学校）